变频环境下异步电机实际转速快速计算方法

刘志峰，石方亮，刘晓鹏，李 磊

（合肥工业大学 机械与汽车工程学院，安徽 合肥 230009）

1 引言

异步电动机的效率优化策略有恒功率因数控制、转差频率控制以及定子电流控制等方法，都属于通过控制电机变频过程实现电机近似效率最优的控制，给电机带来能效提升的同时，也给电机内部机械或电气量的高精准性控制目标提出了挑战[1-4]，电机频率和转速的精确映射目标便是其一。

在工程实际中，应用电机供电频率和电机转速之间的线性映射关系，通过成比例的改变电机供电频率达到所需转速输出的目的。但是由于异步电动机转差率的存在，而且转差率可变，使频率和转速的映射关系并非完全线性[5]，频率对电机实际转速的控制很难达到期望的效果。文献[1-3]所述方法虽然能使电机较精确地输出预期转速，但是需要对电机内部的参变量进行很多复杂的运算和控制。研究表明，异步电动机的转差率和负载相关，负载越大转差率越大，额定状态下，转差率等于额定转差率[6]。而且，转差率是异步电动机在变频调速过程中不可避免的一个参量，所以变频过程本身也是影响电机转差率的因素。研究电机转差率模型，分析异步电动机转差率同负载和频率之间的关系，并进行一定程度的量化表征，是实现异步电动机输出转速精确预测的基础。通过对某型号4极异步电动机变频调速控制过程和实测数据进行分析，确定电机转差率同供电频率和带负载率的相关性，利用统计学方法将其关系拟合成一条简单而有效的经验曲线，并在实验设备上加以验证，实现对电机转差率的量化和“可观可控”，并最终实现给定频率下电机实际输出转速的精确预测。

2 异步电动机变频调速控制思想

开环控制异步电动机变频调速系统流程图，如图1所示。图中：Un和U—变频器的额定电压和变频器的输出电压；fn和f—电网的额定频率和变频器的输出频率；n和T—变频器输出频率为f时对应的电机输出转速和转矩；R，L和C—电机内部的等效电阻、电感和电容。转差率S反映异步电动机工作过程中的转速降落，一定程度上影响电机转子损耗和电机的工作效率，也是影响电机实际转速的众多因素中较难确定的一个，有必要对其进行分析和量化。

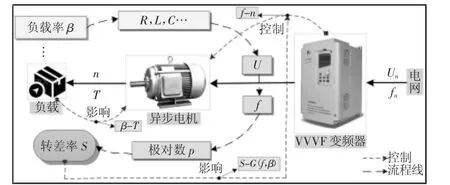
图1 异步电动机变频调速流程图Fig．1 Flowchart of Induction Motor VVVF

通常工程计算中应用异步电动机的调速公式为：

不同频率下，电机相似工况点性能参数变化规律由比例定律确定[7]，即驱动电机的频率改变时，电机转速与频率成比例关系变化：

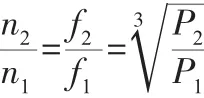
式中：n—电机同步转速；n1和n2—不同工况下的电机转速；f—驱动电机运行的频率；f1和f2—电机的两种工作频率；p—电机极对数；P1和P2—电机不同工况下的输出功率。

异步电动机在运行过程中，由于定子旋转磁场转速和转子转速存在转速差，这种不同步导致了电机转差率的存在。异步电动机实际输出转速是电机同步转速和转差率共同作用的结果，由电机机械特性的普遍规律决定。电机实际调速过程，如式（2）所示。

式中：S—异步电动机转差率。

此时，异步电动机输出机械转矩[8]可以表示为：

式中：CM—与异步电动机结构有关的常数；R2—电机转子回路电阻；U—电机定子线电压；X20—转子转速为零时转子电路的有效感抗。

为保证电动机变频调速获得良好的转矩特性和调速性能，变频调速最常用的控制方式是恒压频比控制，即式（3）可表示为：

式中：k—恒压频比系数，k=U/f。

由式（2）和式（4）可得，同一台电动机工作过程中，频率f和转差率S是决定电机输出转速和转矩的主要因素。进而，变频异步电动机输出功率可表示为：

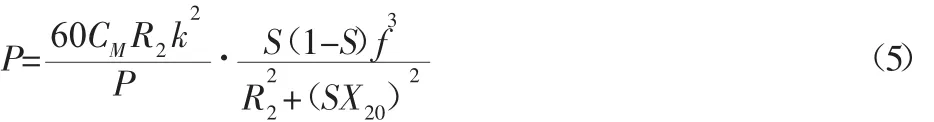
由式（5）进一步得到，频率f和转差率S是影响电机输出功率的因素。在变频调速系统中，电机输出功率是为了匹配负载需求的，能跟随负载状况的改变而变化。把电动机实际输出功率与电动机额定功率之比称为电机带负载率β，如式（6）所示。

式中：P—电动机实际输出功率；Pe—电动机额定功率。

由式（5）和式（6）可得，频率f和转差率S影响电机带负载能力。由于电机转差率S很小，工程实际应用经验表明，1-S可以近似为1。将式（6）代入式（5）并求解S，得到电机转差率S关于频率f和负载率β的表达式：

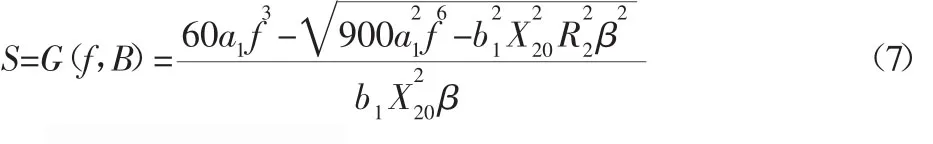
式中：a1=CMR2k；b1=pPe。

综上，在异步电动机变频调速过程中，供电频率和电机带负载率是影响电机转差率的两个主要因素，即影响电机调速过程中转速-频率映射关系精准度的因素。因此，频率f和带负载率β成为量化电机转差率S的两个重要指标。

3 电机实际转速计算方法

3.1 异步电动机转差率测试系统与实测数据

为研究电机转差率S的变化规律，对某型号4极异步电动机的变频调速系统进行测试。通过控制变频器输出如表1所示不同频率，计算各频率对应的电机理想转速n′。调节负载功率至与电机额定功率之比为设定的电机带负载率。通过转速测量仪测量各频率和负载率下电机实际输出转速n，并得到电机转差率S。25组不同频率f、不同负载率β和电机转差率S的对应关系，如表1所示。

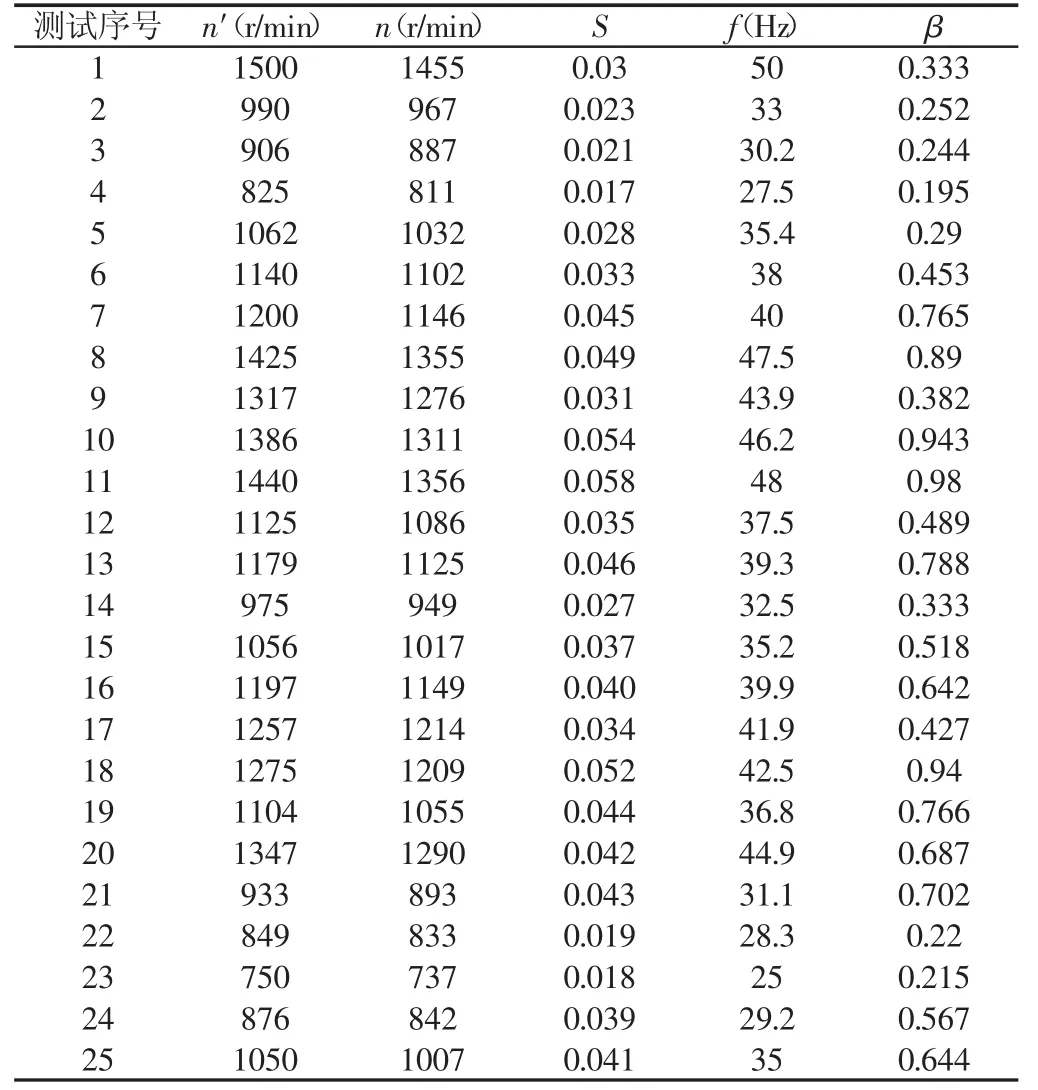
表1 某设备电机转差率、供电频率和电机带负载率的测量数据Tab.1 Experimental Measurements of Slip，Frequency and Load Rate about Motor for Laboratory Equipment

3.2 电机转速经验方程的建立

由表1数据可见，转差率S随供电频率f以及带负载率β的变化，呈现明显的规律性。为避免直接应用式（7）复杂的数学模型，基于统计学规律建立其经验回归平面方程。令y=S，x1=f，x2=β，并设y与x1、x2之间服从线性回归模型：

式中：μ—回归常数；a和b—回归系数；ε—随机误差，服从N（0，σ2），且相互独立。

以表1中实测数据为基础，得变量个数p=2，试验次数n=25。为了求出估计量μ^，a^和b^的值，计算以下和式和均值：

对应于电机转差率S量化成关于频率f和电机负载率β的回归平面方程为：S=0.0063+1.9341×10-4f+0.0413β （9）

式（9）中转差率S与频率f和负载率β是否确有相关关系，最基本的要求是校验回归方程是否显著，故检验统计假设H0：a=b=0。选取统计量设定显著性水平α=5%，则置信水平为95%，计算得的方差分析表，如表2所示。

表2 线性回归方差分析表Tab.2 Variance Table of Linear Regression Analysis

查F分布表得α=5%时，F0.05（2，22）=3.44，即F的计算值远大于其临界值，认为在95%的置信水平下，拒绝假设H0，初步认为经验回归平面方程是十分有效的。将式（9）代入式（2），得电机输出转速n关于频率f和带负载率β的一种有效的经验表达形式。基于转差率回归方程量化方法，电机实际转速n的计算公式可以表示为：

4 电机转速预测和实验验证

为进一步验证所求电机实际转速的表达形式有效，搭建额定功率为5.5kw的4极异步电动机变频调速实验台作为试验对象，应用上述计算方法对电机在各频率点和负载状况下的转速进行快速预测，并在实验台上进行实验测量，实验所用电机和变频器分别，如图2所示。设定电机供电频率为50Hz，将异步电动机转速-负载率回归方程预测曲线与传统离散点实验方法所获得的实测曲线对比，如图3所示。实验中负载率依次取0.3、0.4、0.5、0.6、0.7、0.8 和 0.9，此时回归方程预测电机转速的曲线方程为：n=-61.95β+1476.0443

图2 实验测试系统装置Fig.2 Devices for Experimental Test

图3 50Hz时电机转速-负载率预测曲线与离散点实测曲线对比Fig.3 Comparison about n-β Curves of Prediction and Experiment Results with f=50Hz

设定电机带负载率为1.0，将异步电动机转速-频率回归方程预测曲线与传统离散点方法实验所获得的实测曲线对比，如图4 所示。实验所用频率依次取 25Hz、30Hz、35Hz、40Hz、45Hz和50Hz，此时回归方程预测电机转速的曲线方程，如图4所示。部分频率和负载率下电机输出转速的回归方程预测值和实验测量值的对比，结果显示回归方程预测值与实验测量值的误差率在0.5%以内，如表3所示。表3还列出了由比例定律确定的电机转速传统理论值，结果显示与实验测量值相差较大。

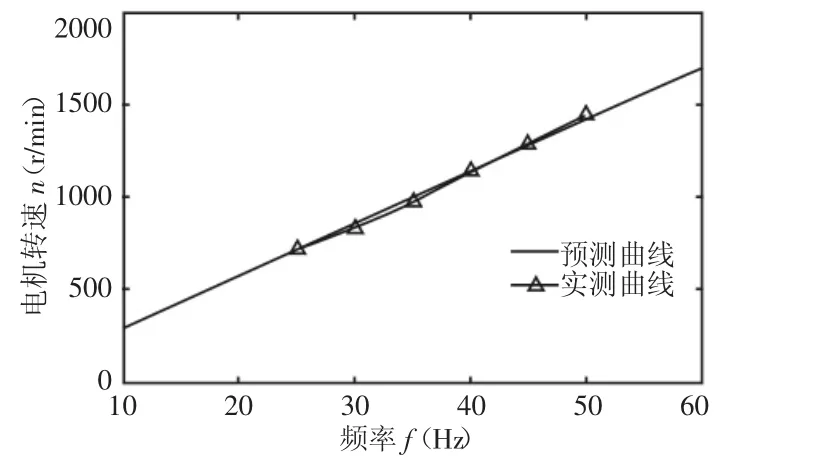
图4 负载率为1.0时电机转速-频率预测曲线与离散点实测曲线对比Fig.4 Comparison about n-f Curves of Prediction and Experiment Results with β=1

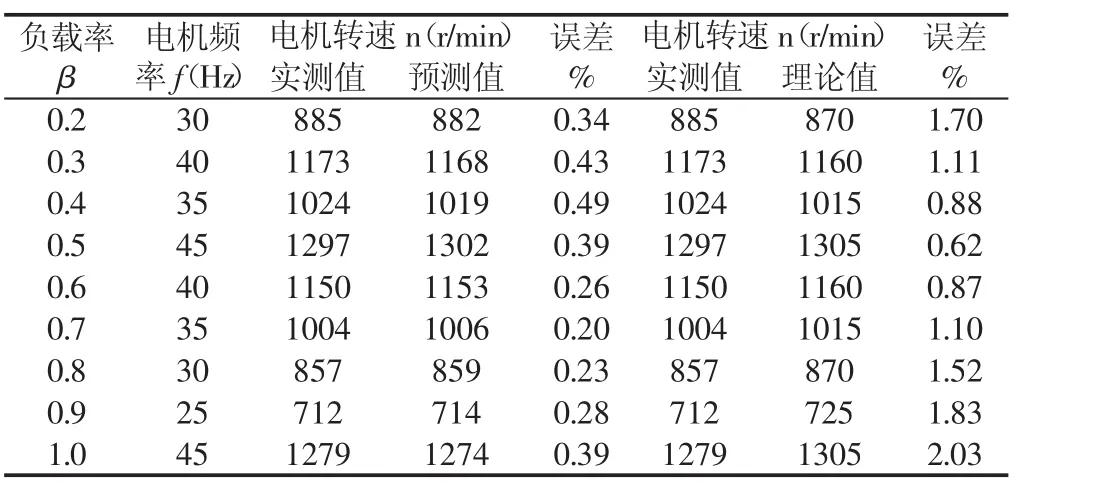
表3 异步电机变频调速转速回归方程预测值、传统经验值与实测值对比Tab.3 Comparison of Regression Equation Predicted Values，Traditional Experienced Values and Measured Values About Speed of Induction Motor Frequency

由图3和图4所得电机转速实测曲线与回归方程预测曲线对比结果及表3中数据对比可以看出，电机转速回归方程预测结果与实验测量结果相吻合，误差都控制在0．5%以内，电机带负载率在（0．6～0．8）时误差更小，与实测数据的吻合度更高；由比例定律确定的电机转速与实验测量结果相比，误差基本都在1%以上。回归方程预测电机转速的方法对电机在给定转速（或频率）下的实际供电频率（或输出转速）预测提供了量化公式，解决了变频调速系统功率匹配过程中电机输出转速不准确的问题。但是还存在一定的误差，分析其原因如下：（1）在公式理论推导过程中，将电机定子与转子上的各等效参数都视为恒定值，认为电机的转速只跟供电频率和转差率有关系。然而异步电动机在实际运转过程中内部参数会随着环境（比如温度）的变化而改变，尤其在电机长时间测试发热严重时，变化更加明显。因此造成预测公式存在一定的误差。（2）在电机实验测试过程中，电网质量对电机工作状况有直接影响，如电压波动、三相电压不平衡、电网中含有谐波等，都会导致异步电动机输入电源质量的差异，导致实验测试存在误差。

5 结论

从异步电动机转速、转差率、供电频率以及带负载情况的相互关系出发，建立异步电动机变频调速过程中电机转差率-频率/负载率的理论模型。基于某型号异步电动机变频调速过程采集的大量数据，用统计学方法拟合了电机转差率-频率/负载率的经验回归方程，进而建立了异步电动机调速过程中电机转速-频率/负载率的实际映射关系模型。该模型只需取得负载需求的电机转速（或变频器给定的供电频率）和所带负载率，应用所得模型即可快速地、准确地预测变频系统实际需要提供的供电频率（或电机实际输出转速），实现供电频率对电机转速的精准控制，应用效果如图5所示。将该模型预测电机输出转速的方法和传统比例定律确定转速的方式同实验测量结果对比，表明转速预测方法的精准性优于比例定律，且与实验测量误差在0．5%以内，电机带负载率在（0．6～0．8）时预测效果更佳。该方法克服了电动机变频调速过程中输出转速与预期转速误差大以及传统的控制过程复杂等问题，为后续电动机其他参变量的精准控制提供了经验参考。

［1］Anderson H R，Pedersen J K．Low cost optimized control strategy for a variable speed three phase induction motor［C］．Conf．Rec．PESC’96，1996（1）：920-924．

［2］贾贵玺，陈起．小功率发电机励磁系统的恒功率因数控制［J］．电机与控制学报，2006，10（6）：567-570．（Jia Gui-xi，Chen Qi．Constant power factor control for excitation system of the small synchronous generator［J］．Electric Machines and Control，2006，10（6）：567-570．）

［3］樊扬，瞿文龙．基于转子磁链q轴分量的异步电机间接矢量控制转差频率校正［J］．中国电机工程学报，2009，29（9）：62-66．（Fan Yang，Qu Wen-long．Slip frequency correction method base on rotor flux q axis component for induction machine indirect vector control system［J］．Proceedings of the CSEE，2009，29（9）：62-66．）

［4］傅彩明，谭加才．立式电机定子模态有限元仿真及试验研究［J］．机械设计与制造，2007，8（8）：159-160．（Fu Cai-ming，Tan Jia-cai．Model experimental research and finite element analysis of vertical motor［J］．Machinery Design and Manufacture，2007（8）：159-160．）

［5］曹玉泉，闫丽梅．变频调速异步电动机的转差率［J］．西南交通大学学报，2006，41（1）：37-41．（Cao Yu-quan，Yan Li-mei．Slip of induction motor with frequency speed control［J］．Journal of Southwest Jiaotong University，2006，41（1）：37-41．）

［6］刘军华，李春茂．转差率控制的异步电动机调速系统的设计［J］．电气传动，2008，38（5）：22-24．（Liu Jun-hua，Li Chun-mao．Design of asynchronous motor variable frequency speed regulating system based on slip［J］．Electric Drive，2008，38（5）：22-24．）

［7］马燕，吴韬．异步电动机的转速公式与功率控制调速理论［J］．西北民族大学学报：自然科学版，2005，26（56）：21-25．（MaYan，WuTao．Inductionmotorspeedcontrolandpowerequationtheory［J］．Journal of Northwest University for Nationalities：Natural Science，2005，26（56）：21-25）

［8］秦曾煌．电工学（上册）（第六版）［M］．北京：高等教育出版社，2004：211-212．（Qin Zeng-huang．Electrical Engineering（Sixth）［M］．Beijing：Higher Education Press，2004：211-212．）