Matlab在函数辅助学习中的应用
2018-03-21陈建宇
陈建宇
(石家庄市第一中学,河北石家庄050010)
0 引言
二次函数图像和斜面平抛运动性质的知识点是高中数学、物理学习的重要内容,传统的基于教材的学习方式无法呈现出函数的运动和变化过程,更难以绘制出准确的函数图像,使得函数图像与函数性质之间的关系难以理解[1]。为此,采用基于软件工具的图形化显示研究方法,辅助直观深入理解这些内容。国际上,数学类软件工具主要有Matlab、Mathematica和Maple,其中Matlab是美国Math Works公司出品的数学软件,因其提供计算、图形和文字处理的统一环境而深受中学生欢迎[2]。利用其数学分析以及可视化性能的优越性,可以将抽象的问题形象化,从而加深对问题相关结论的理解,使学习内容之间的联系更为突出。
1 二次函数图像性质研究
二次函数的定义是一个二次多项式,一般式为=2+ +(≠0),其中 为二次项系数且不等于零。在二次函数性质中,开口方向、大小与二次项系数的关系可以通过Matlab编程调整参数,实现一次性绘制多组二次项系数的二次函数曲线[3-5]。主要过程为:针对需要研究的问题确定参数,实现含参数变量的二次函数,确定绘图范围,按给定参数值调用绘图函数,改变参数值循环执行上述步骤。为简化问题,固定 和 的值,设定5组不同的 值,如表1所示。
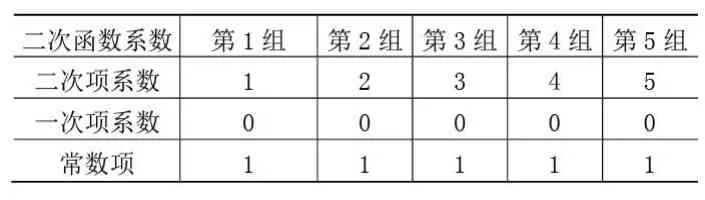
表1二次函数参数设置
按照参数设置,采用Matlab的绘图函数,可一次绘制出5组二次函数曲线,如图1所示。
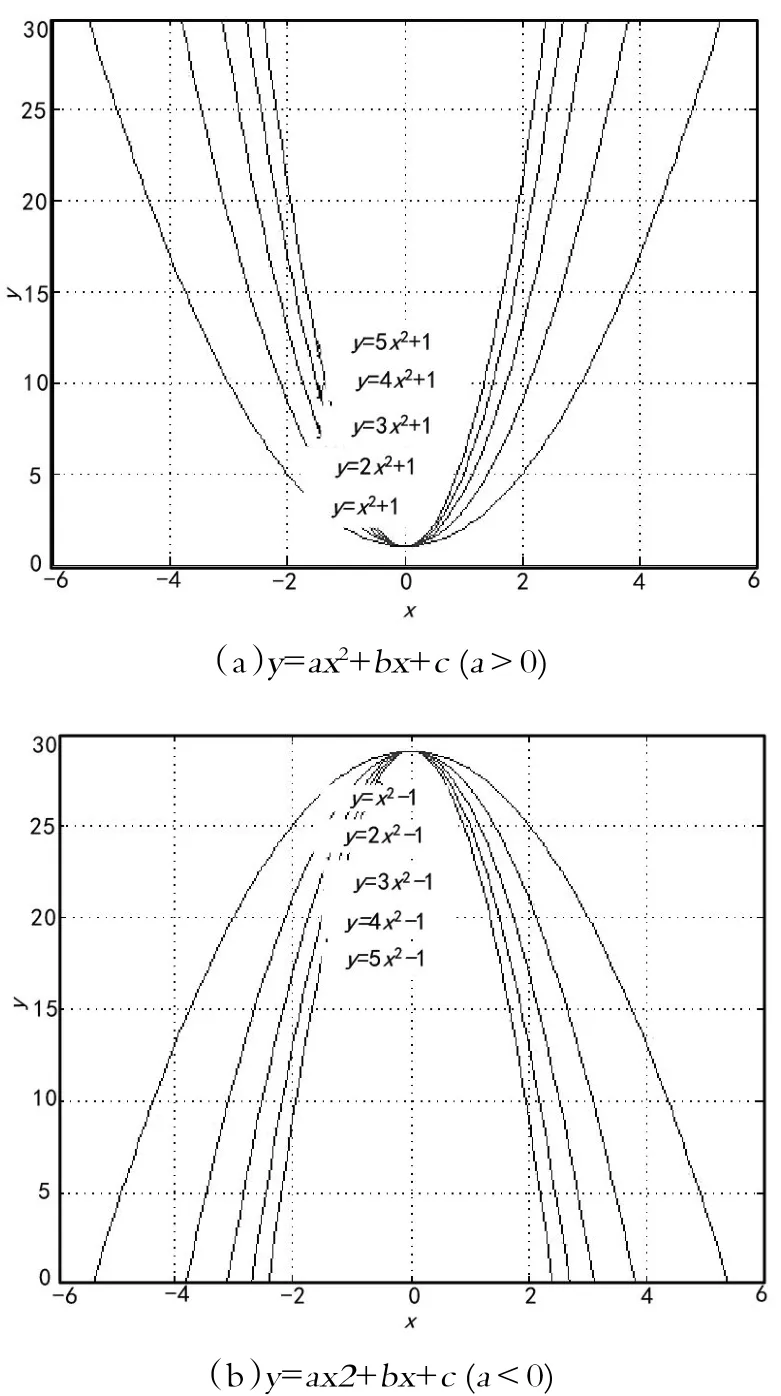
图1二次函数图像
从图1中可以看出,>0时,二次函数图像开口向上;<0时,二次函数图像开口向下;随着||的增大,二次函数图像开口变大,随着||的减小,二次函数图像开口变小。
Matlab主要程序如下[3]:
for=[1,2,3,4,5];%循环 5组
plot(,); %绘制函数曲线
grid on
axis([-6,6,0,30]);
pause(1) %间隔1 s
hold on
end
2 斜面平抛运动性质研究
利用上述二次函数图像性质研究方法可以进一步研究斜面平抛运动性质问题,在理论证明末速度方向与平抛初速度无关的基础上,采用Matlab编程显示不同平抛初速度情况下的抛物轨迹,计算并绘制抛物落点的速度方向,提供形象化研究支撑[3-5]。
(1)原理证明
设 为位移偏向角,由于小球从斜面顶端平抛且落在斜面上,这里 也就等于斜面与水平面夹角,故 为定值;
为速度偏向角;_0是平抛初速度,_是末速度在竖直方向上的分量;、分别代表水平、竖直方向位移;表示平抛全过程所用时间,证明如下:
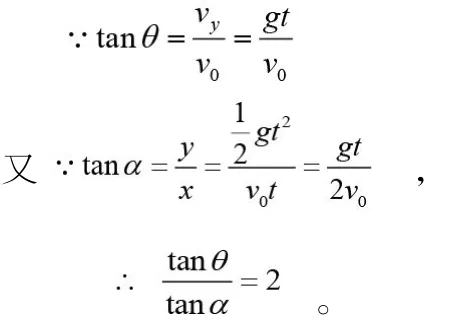
式中,因 为定值,所以 为定值,末速度方向始终相同,与平抛初速度无关。
(2)斜面及抛物轨迹绘制
在Matlab中通过绘制一次函数模拟斜面,使之过定点(0,50),可根据一次函数斜率大小调整斜面陡缓。在Matlab中通过绘制二次函数 =2+ + 图像中部分曲线模拟小球由斜面顶端平抛下落至斜面的运动轨迹,通过固定一次项系数和常数项 的值,将二次函数对称轴锁定在 轴处,并使之过定点(0,50),这样可保证小球从斜面顶端平抛,图像中对称轴右半段单调递减部分为小球由斜面顶端平抛下落的运动轨迹,计算与绘图方法与二次函数相同。
(3)参数调整
可根据二次项系数(<0)绝对值大小的改变模拟该实验中不同的平抛初速度:随着||的增大,二次函数图像开口变大,平抛初速度增大;||减小,图像开口变小,平抛初速度减小。为简化问题,固定 和 的值,设定3组不同的平抛二次项系数模拟不同的平抛初速度,如表2所示。
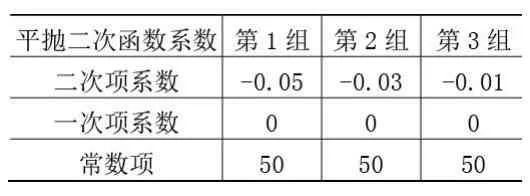
表2平抛二次函数参数设置
(4)末速度方向绘制
①利用Matlab中求解方程组的功能,计算出小球在斜面上落点处的坐标;
②根据物理学中常用的微元法,可以从小球在斜面上的落点处附近的二次函数图像上取间隔极近的2点,利用这2点求出落点处的一条二次函数图像切线,即为末速度方向。
这里需要说明的是,由于小球必须从斜面顶端抛下,才能使此推论成立,所以上文所述一次函数与二次函数的交点会出现2个,即平抛初始位置和落点处,由此引发的问题是:若仅依据两函数交点坐标绘制切线,那么其中一条将始终过点(0,50),而这条切线没有实际意义。
为了排除这个问题,对Matlab求解方程组时用到的Solve函数进行深入分析,发现其输出是一个数组,确知2组解的话,取出其中某一组应是[(1),(1)]、[(2),(2)],所以可以直接取[(2),(2)]进行切线的计算和绘制,运行结果如图2所示。
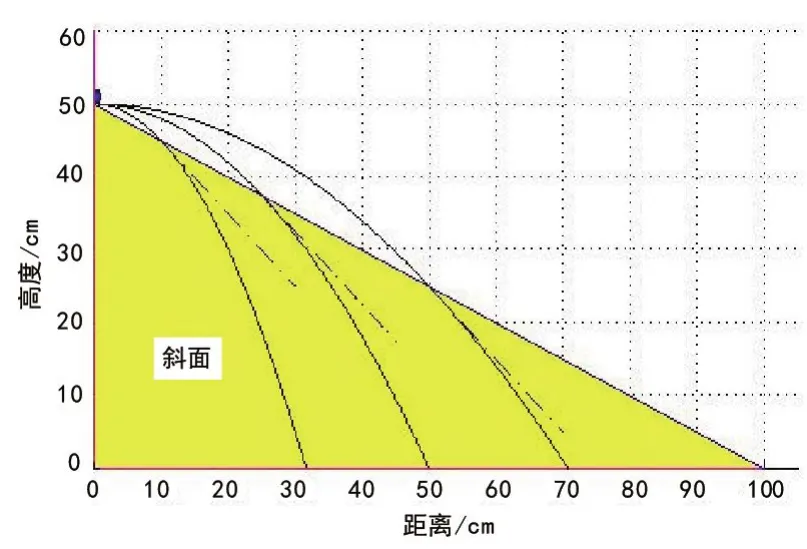
图2斜面平抛运动
图2中,虚线即绘制出的切线,表示小球末速度方向,可以看出,随着平抛初速度的增大,小球落在斜面上的位置不断变化,但切线相互平行,末速度方向始终不变。
Matlab主要程序如下:
for=[-0.05,-0.02,-0.01];
%绘制平抛曲线%
plot(,1,'',1,,'',,,'black');
grid on
hold on
%绘制落点切线%
[,]=solve([num2str(a),'⋆ ⋆ +50-=0'],'50-0.5⋆ -=0','','');
plot(,,'-.') %绘制切线
end
3 结束语
利用Matlab进行函数及应用问题的学习探究,可以化抽象为具体,为培养数形结合的数学思想提供方便易用的工具。除本文主要利用的Matlab对函数性质分析的图形化显示和求解方程组的功能外,还探索了其他诸如绘制马鞍形曲线和三角函数曲线等人们难以理解和绘制的图像,体会到了其优越的可视化性能。
[1]董雪瑶,郑春香.MATLAB在高中数学研究性学习中的应用研究[J].信息技术与信息化,2016,9(9):92-95.
[2]李冰,吴迪.将MATLAB软件在高中数学教学中进行推广的几点设想[J].计算机教学与教育信息化,2014,10(5):3033-3036.
[3]刘浩,韩晶.MATLAB R2012a完全自学一本通[M].北京:电子工业出版社,2013.
[4]王亚芳,等.MATLAB仿真及电子信息应用[M].北京:人民邮电出版社,2011.
[5]王中鲜,等.MATLAB建模与仿真应用教程(第2版)[M].北京:机械工业出版社,2014.
