复杂组合截面曲线梁桥简化有限元模拟方法研究

许逸雪,高燕梅,周志祥,李 勇

（1.山区桥梁结构与材料教育部工程研究中心，重庆 400074；2.重庆交通大学 土木工程学院，重庆 400074；3.深圳桥博桥梁设计研究院有限公司，深圳 518052）

钢材具有质轻高强的特点，将其折叠后形成波形钢板取代箱梁混凝土腹板，解决了箱梁腹板开裂的同时，大大提高了结构的抗剪能力［1，3］，使得波形钢腹板组合箱梁桥一出现便在工程上得到广泛的应用。然而，波形钢腹板组合箱梁底板混凝土浇筑施工难度较大，在荷载作用下易过早开裂，提出将钢管混凝土取代波形钢腹板组合箱梁中的混凝土底板，不仅进一步减轻了主梁自重，提高了结构抗裂性和整体性，同时有效地提高了预应力效率［4，6］。随着交通行业的发展，逐渐出现了正交异性钢桥面板-波形钢腹板-钢管混凝土组合梁桥，该结构绝大部分使用钢材，施工一体化程度高，可用于一些中小跨径桥梁、环形人行天桥，实现快速施工。对于这种新型组合结构，无论是理论研究，还是工程应用，有限元模型的计算分析均成为必不可少的环节。由于正交异性钢桥面板、波形钢腹板、钢管混凝土这3种构造运用于曲线梁桥中，相互间接触关系模拟较为复杂，会遇到如何建立反映实际结构的有限元模型的问题，而目前对此类结构的有限元模拟方法研究则相对匮乏。李果、樊健生在ANSYS有限元程序中将钢结构采用壳单元模拟，管内混凝土采用实体单元模拟［7］。陈宝春、陈宜言在ABAQUS有限元程序中将钢结构与管内混凝土采用实体缩减积分单元模拟，并利用缩减积分壳单元模拟钢结构［8］。虽然上述方法都是正确有效的，但是利用ANSYS或ABAQUS有限元程序的常规模拟方法会使计算模型单元数量多，接触关系复杂，使得建模工作繁重且计算速度较慢，并且上述两种方法很难模拟钢与混凝土随着施工阶段的推进，先后参与受力的状态。

为了简化桥梁计算，减少建模工作，同时模拟施工阶段的结构受力，可采用Madis Civil有限元程序进行模拟分析，而现有研究中Madis Civil仅能模拟波形钢腹板-混凝土组合结构，基于此，本文针对正交异性桥面板-波形钢腹板-钢管混凝土这种复杂截面的组合曲线梁桥，进行了简化有限元模拟方法研究。

1 桥型构造特点

某人行天桥上部结构采用组合连续梁，由正交异性桥面板、波形钢腹板及钢管混凝土下弦杆组成，如图1所示。与传统的组合箱型结构不同，该结构的截面构造特色如下：

曲线梁桥以波形钢腹板替换传统的直腹板，可使桥面不设置伸缩缝，通过波形钢腹板的伸缩调节由温度引起的变形；由于波形钢腹板的皱褶效应，对主梁的纵向抗弯贡献可忽略不计，仅考虑正交异性桥面板与钢管混凝土参与受力。

采用正交异性钢桥面板代替传统的混凝土桥面板，便于钢结构整体吊装，简化了施工工序，缩短了施工周期。

主梁下弦杆中灌注微膨胀混凝土，混凝土对钢管的作用使得钢管自身的刚度和稳定性得到提高，从而提高了结构的整体抗弯刚度和稳定性。考虑主梁混凝土不参与受力，仅提高结构的稳定性。

人行天桥桥面较窄，采用三角形截面，提高了桥梁抵抗横向风力的能力。

简化了施工工序后，该结构具有如下的施工特色：先完成钢结构的架设，由钢管承受混凝土的重量，当混凝土达到设计强度后，成为钢管混凝土组合结构参与后期的受力。

2 有限元模型的建立方法

针对这种复杂截面，可分别输入正交异性钢桥面板、波形钢腹板及钢管混凝土截面，建立三层单元进行模拟，计算模型单元数量多，建模工作繁重。同时曲线梁中波形钢腹板对于正交异性钢桥面板与钢管混凝土为连续相连构件，导致三层单元间的连接模拟复杂，若将上下层单元竖向连接，则无法模拟连续的波形钢腹板对上下结构的影响。基于此，对该类复杂截面提出了一种简化模拟方法。

2.1 正交异性钢桥面板的简化模拟

波形钢腹板组合箱梁抗扭转刚度较传统混凝土箱梁小，需设置一定数量的横隔板，当横隔板间距较大且桥宽较小时，被横隔板隔断的正交异性钢桥面板为单向板受力。考虑主受力方向的加劲肋承受正截面受弯承载力的作用，将正交异性钢桥面板纵向加劲肋在截面中直接建立，横向加劲肋则通过修改截面特性来模拟其刚度的影响，重量的模拟通过容重乘以系数实现。

2.2 波形钢腹板的简化模拟

横截面输入时以直钢板代替波形钢腹板（如图2所示），钢板厚度采用原厚度，通过修改截面特性来考虑波形钢腹板形状对结构顺桥向刚度的影响，且波形钢腹板不参与纵向抗弯，所以计算抗弯惯性矩时不考虑波形钢腹板。

但波形钢腹板对扭转惯性矩的影响是需要考虑的，因此取波形钢腹板一个节段，长度L。将截面分为两部分，S1和S2（如图3所示）。

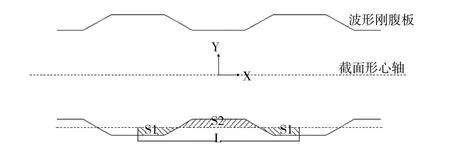
图3 计算示意图

在一个节段内两侧波形钢腹的影响：

考虑单位长度内的惯性矩：

考虑波形钢腹板对扭转惯性矩的影响，最终的惯性矩为:

式中：IS1，IS2分别为S1、S2区域对形心轴X轴的惯性矩；Ix为简化后截面对形心轴X轴的惯性矩。

该方法通过修改梁单元的截面特性模拟波形钢腹板顺桥向对桥梁受力的影响，解决了Madis Civil模拟波形钢腹板用在复杂截面里的局限性，如需考虑波形钢腹板局部应力，可另外建立局部精细化模型。

2.3 钢管混凝土的简化模拟

钢管混凝土在复杂截面中，混凝土模拟困难，若建立钢管混凝土单元，则三层单元间的连接模拟复杂且无法真实反映波形钢腹板对钢管混凝土的影响，基于此，提出以下两种方法进行简化。

2.3.1 换算截面法简化

首先建立单梁单元，将两种材料组合成的实际截面换算成一种拉压性能相同的假想材料组成的匀质截面，保证换算截面后的形心轴不变，将管内混凝土转化为与管径等高的矩形钢板（如图4所示），计算换算后的截面面积与惯性矩，通过修改截面特性来计入下弦钢管内灌注的混凝土对截面面积和刚度的影响。管内混凝土重量作为均布荷载考虑，施加在钢梁单元上。

式中：AS为钢板面积；AC为混凝土面积；EC为混凝土弹性模量；ES为钢板弹性模量。

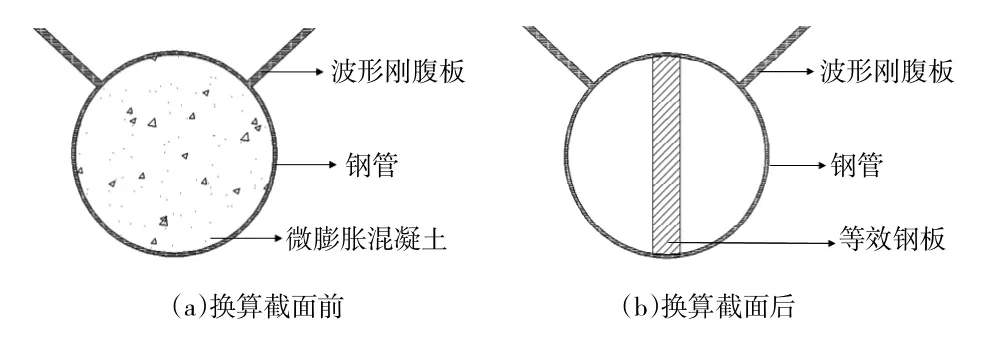
图4 单梁单元简化示意

建立单梁单元的换算截面法，简化了建模工序，但无法模拟先钢管后混凝土的施工工序，适用于成桥受力性能分析、稳定性分析的简化模拟。

2.3.2 钢结构-混凝土双单元简化

为了体现结构的时间维度特征，准确模拟钢管混凝土的施工过程，可采用双单元方法（如图5所示）：首先建立复杂截面的钢结构单元，并承受自重作用；将混凝土重量作为外荷载施加在钢结构单元上，以此模拟混凝土浇筑时，混凝土自重由钢结构承受的阶段；最后安装混凝土单元，单元位置位于下弦形心处，钢结构单元与混凝土单元之间采用刚臂单元连接，以此形成复杂钢结构截面-混凝土组合结构承受后期荷载。

图5 双单元简化示意

建立双单元的模拟方法概念简单，便于考虑钢管混凝土施工中构件的受力情况，适用范围更广；但施工时混凝土的重量通过刚臂单元施加到钢梁上，刚臂间节段等效为梁的受力，仅在支点间传力，需要减小刚臂单元间间隙模拟结构真实的受力。桥梁结构的受力随着施工方法与施工进程的改变而变化，因此，在分析时考虑施工过程能得到更为准确的成桥使用状态受力性能，采用了双单元模拟的方法进行建模。

2.4 有限元模型的建立

某环形人行天桥全长330 m，桥面全宽6.4 m，主桥桥跨最大跨径51 m，材质采用 Q345q-C，混凝土C50。根据上述简化模型建立方法，运用Madis Civil程序建立了全桥有限元模型，如图6所示。按照结构离散化以及节点位置选择的基本原则，对桥面进行划分；建立钢结构-混凝土双单元，将波形钢腹板简化为直钢板，通过修改截面特性计入正交异性钢桥面板横肋及波形钢腹板顺桥向对桥梁受力的影响；桥墩底位置处采用全固结方式，墩梁固结处用刚臂来模拟；同时，根据施工的总体安排，将施工阶段划分如下:桥墩钢管施工，Y上部钢管施工，钢主梁安装，灌注主梁下弦混凝土，主梁混凝土参与受力，二期铺装，10年收缩徐变。

图6 全桥模型

3 全桥分析结果

对上文建立的有限元模型，在自重、温度荷载、风荷载、人群荷载及支座强制位移的组合作用下的结构响应进行了计算，结果如图7、图8所示。

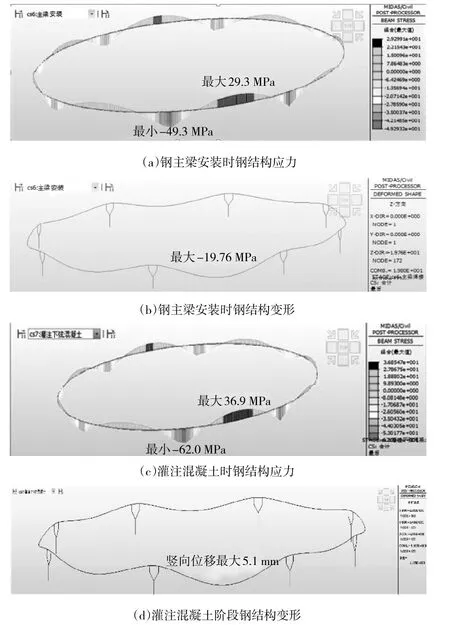
图7 关键施工阶段分析结果

根据图7可以看出，灌注混凝土时主梁钢结构的力学响应及其变化。对于主梁混凝土，考虑其不参与受力，仅提高结构的稳定性，则施工阶段混凝土的力学响应未示出。利用该模拟方法，可以对钢混结合区的力学响应进行全过程分析，力学概念清晰，而这是传统精细有限元模型难以实现的。在桥梁施工时，可分别得到各阶段结构的变形情况，对于主梁钢结构，各施工阶段最大变形为-19.76 mm（发生在钢主梁安装阶段最大跨跨中钢结构下缘），施工完成后，主梁钢结构最大变形-28.21 mm（发生在最大跨跨中钢结构下缘）；在形成钢混组合结构参与后期受力时，可分别得到钢结构与混凝土的应力（如图7（a）、8（b）所示）。对于主梁钢结构，组合最大压应力为103.1 MPa(发生在支点处钢结构下缘)，组合最大拉应力为68.1 MPa（发生在最大跨跨中钢结构下缘）。根据文献，Q345钢的容许应力为200.0 MPa，有限元简化模拟结构的应力计算值均没有超过规范值，说明该桥的强度满足要求［9］。利用该方法，能够得到钢结构截面和混凝土截面整体受力情况，但对于曲线桥梁，从图8（c）可以看出，结构承受弯扭剪的共同作用，要考察结构的局部受力，只需另外建立直线节段精细化模型计算，而不必建立整体曲线桥梁模型，由此计算简化。

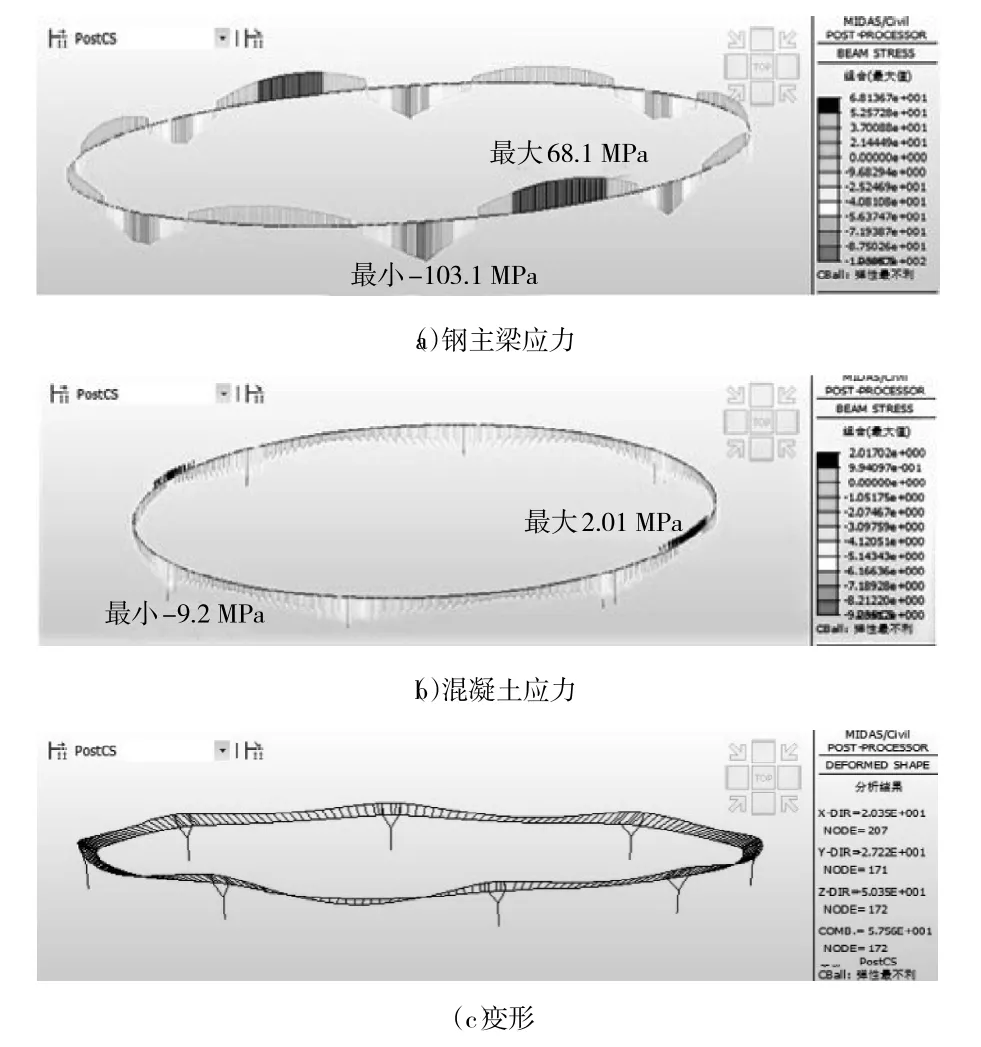
图8 正常使用极限状态分析结果图

4 结论

（1）相比常规组合梁，基于复杂截面的钢-混凝土组合曲线梁桥有3个构造特点：①采用正交异性钢桥面板，便于钢结构的整体吊装；②桥面不设伸缩缝，采用波形钢腹板调节温度产生的变形③主梁下弦采用钢管混凝土结构。由此减少了现浇混凝土的养护时间，加快了施工一体化进程，实现快速施工。

（2）提出了一种适用于由正交异性桥面板、波形钢腹板、钢管混凝土组成的复杂截面的组合曲线梁桥的简化有限元模拟方法。采用Madis Civil建立有限元模型，通过修改梁单元的截面特性，模拟正交异性钢桥面板横肋对结构刚度的影响；采用以直代曲的方式简化波形钢腹板，并将其顺桥向对桥梁受力的影响通过修改梁单元的截面特性的方式计入；采用建立钢结构-混凝土双单元的方法实现钢管混凝土施工工序的模拟，解决了由ANSYS和ABAQUS等程序计算时施工阶段模拟困难且单元众多、计算速度较慢的问题。

（3）利用提出的简化模拟方法建立了某环形人行天桥的有限元计算模型，分析了组合曲线梁桥从施工到成桥到运营阶段的力学行为，结果表明：该简化模拟方法能较真实地模拟结构的截面特性，可分析得到考虑施工过程后更为准确的结构受力性能，综合多个薄弱构件的力学响应，适用于此类桥梁的简化计算，可为同类桥梁提供相关参考。

［1］Mohamed Elgaaly. Bending Strength of Steel Beams with Corrugated Webs［J］. Journal of Structural Engineering，1997，123（6）：772-782.

［2］Elgaaly M，Seshadri A, Hamilton R W. Beams with corrugated webs，research to practice［C］∥Research Transformed into Practice@sImplementationof NSF Research. ASCE，2015：601-623.

［3］Metwally A E, Loov R E. Corrugated steel webs for prestressed concrete girders［J］. Materials and Structures， 2003，36（2）：127-134.

［4］乔晋姿，祝兵.波形钢腹板PC组合箱梁发展综述及受力分析［J］. 四川建筑科学研究，2008，34（4）：49-52.

［5］董桔灿，陈宜言，BRISEGHELLA Bruno，等.波形钢腹板-双管弦杆-混凝土板组合连续箱梁受弯性能［J］. 交通运输工程学报，2016，16（3）：35-45.

［6］陈宝春，高婧.波形钢腹板钢管混凝土梁受弯试验研究［J］. 建筑结构学报，2008，29（1）：75-82.

［7］李果，樊健生.波形钢腹板—钢管混凝土组合梁桥受力性能研究［C］∥上海：第十九届全国桥梁学术会议中国土木工程学会桥梁及结构工程分会，2010：949-954.

［8］王梦雨.波形钢腹板—双管弦杆—混凝土板组合梁抗弯性能研究［D］.福州：福州大学，2012.

［9］JTG D64—2015公路桥涵钢结构及木结构设计规范［S］.

［10］CTT 69—1995城市人行天桥与人行地道技术规范［S］.