基于关键帧和局部极值的手势特征提取算法
2018-03-20刘杨俊武程春玲
刘杨俊武,程春玲
(南京邮电大学 计算机学院,江苏 南京 210003)
0 引 言
动态手势包含运动轨迹变化和结构变化等,准确的识别动态手势需要研究动态手势特征提取算法,用于表达手势的运动轨迹特征和结构特征。根据提取的特征类型不同,目前的动态手势特征提取算法主要分为基于图像属性的动态手势特征提取算法和基于几何结构的动态手势特征提取算法。其中,基于图像属性的手势特征提取算法是利用目标检测算法提取出图像的像素点分布情况来表达手势,常用方法包括Hu矩[1]、梯度方向直方图(histogram of oriented gradient,HOG)[2]、光流直方图(histogram of optical flow,HOF)[3]等。这些算法计算较为简便,且易于实现,但是提取出的特征维度较大,会增加手势识别的计算量和计算时间。基于几何结构的手势特征提取算法是对图像原始数据进行处理,提取出能够反映手势本质的结构信息,有利于区分手势,提高手势识别的准确性,主要方法包括结构特征点[4]、凸包[5]、k-曲率[6]等。但是该类算法的计算复杂度较高,计算时间较长。
为了缩短手势特征提取的时间,Hasan等通过两种半径大小不同的动态圆模板区分出手势的手掌区域和手指区域,然后根据各个区域中的动态圆模板分布确定手势中的指尖、指根以及手掌中心的位置[7]。但是该算法易受到噪声数据的干扰,识别准确性不稳定。Huang等提出一种基于套索的手势特征提取算法,通过设置一个固定宽度的套索,并对手势轮廓上的每个峰值点进行遍历,若轮廓的宽度与套索的宽度相同,则认为该段为手势的一个手指[8]。这种方法的不足是套索宽度的设置依赖人的先验知识,可能造成误差或者漏查手指的情况,导致手势识别的准确性降低。文献[9]提出一种基于凸包缺陷的动态手势特征提取算法。该算法对于凸包中的每一个凸包缺陷,根据它的起始点、中心点、距离最远点以及最远点到凸包的距离四个特征之间的相互关系,判断是否存在指尖点。但是该算法只能计算出指尖的个数,并不能获取指尖点的位置信息,且易受到噪声数据的干扰,对于相似的手势类型识别正确率较差。文献[10]认为传统基于k-曲率的指尖特征提取算法会受到曲率较大的非指尖特征点的干扰,降低识别的准确性,因此提出一种改进算法,在筛选出曲率较大的候选指尖点集后,采用聚类算法将候选指尖点划分成多个子集,并选择每个子集中的中位点表示指尖位置。但是该算法需要依赖人为设置的曲率阈值,并且对候选指尖特征点集进行聚类过滤需要消耗较长的计算时间。
此外,还可以通过减少手势特征提取的次数来缩短动态手势特征提取的时间。文献[11]提出一种基于关键帧的手势特征提取算法,通过计算和比较相邻帧手势图像的质心距离,选择出距离大于阈值的手势图像进行特征提取。Tan等认为具有较小变化的手势图像能够反映手势序列的关键信息,因此提出通过计算相邻帧手势图像之间像素点的变化个数,将像素点近似不变的手势图像作为关键帧[12]。虽然该类方法可以缩短特征提取的计算时间,但是关键帧选取阈值的设置会影响手势识别的准确性和实时性,由于不同动态手势的运动速率存在差异,很难确定合适的阈值。
因此,针对动态手势特征提取算法计算时间较长的问题,文中提出一种基于关键帧和局部极值的动态手势特征提取算法,并通过实验对其进行验证。
1 基于关键帧和局部极值的动态手势特征提取算法
动态手势特征提取算法可以看成是对一组手势图像采用静态手势特征提取算法进行手势特征提取的过程,算法的计算时间取决于特征提取的次数和特征提取的计算量。为了缩短手势特征提取过程的计算时间,文中算法的基本思想是从手势视频中选出具有较强区分能力的手势图像,并提取这些图像中的质心特征和指尖特征,用于表达手势的运动轨迹和外形结构。
在进行手势特征提取之前,首先需要对获取的手势图像进行手势分割,获取手势的轮廓。由于肤色在HSV颜色空间中具有良好的聚类特性,采用文献[13]提出的基于肤色的手势分割算法,从手势视频的每一帧手势图像中分割出手势区域,然后采用基于Canny算子的轮廓检测算法得到手势轮廓[14]。
1.1 基于运动方向和自适应阈值的关键帧手势图像选取算法
由于动态手势运动轨迹中运动方向发生改变的手势数据能够充分描述该手势的运动轨迹特征,对这些特征点进行提取可以提供区分手势的重要信息。另一方面,均值能够反映数据集中的一般变化程度,可以通过计算当前帧手势图像之前所有质心距离的均值,确定关键帧手势图像选取阈值的大小。因此,提出一种基于运动方向和自适应阈值的关键帧手势图像选取算法。
首先计算出相邻帧手势图像之间的相对运动方向,相对运动方向通过质心之间的偏移角度θt确定,根据θt将手势运动划分成八个不同方向,其计算公式如下:
dirt=
(1)
其中,dirt为第t帧手势图像的方向码值。
若dirt≠dirt-1,说明动态手势的运动方向发生改变,则将当前帧手势图像作为一个关键帧手势图像进行特征提取。否则表示动态手势的运动方向没有发生改变,通过计算相邻帧手势图像的质心距离,将距离大于阈值的手势图像作为关键帧。
由于动态手势具有不同的运动速率,为了降低人为设置阈值参数对手势特征提取准确性的影响,关键帧手势图像选取阈值的大小应根据手势运动轨迹的变化程度动态调整。其基本思路是在每次比较相邻帧手势图像之间的质心距离后,根据式(2)和式(3)计算出当前帧手势图像之前所有质心距离的平均值,作为新的关键帧手势图像选取阈值。
(2)
dist(t1,t2)=|gt1-gt2|
(3)
其中,δt表示第t帧的关键帧手势图像选取阈值;dist(t1,t2)表示第t1帧和第t2帧手势图像之间的质心距离。
基于运动方向和自适应阈值的关键帧手势图像选取算法伪代码描述如下:
算法1:KeyFrameSelect(It)
输入:手势图像It
输出:关键帧手势图像标记iskeyframet
1.iskeyframet←1;//初始化关键帧手势图像标记
2.calculategt;//计算质心
3.calculate dirtusing Eq.(1);//计算运动方向
4.if(dirt==dirt-1) //判断运动方向是否相同
5.calculate dist(t,t-1)using Eq.(3);//计算质心距离
6.if(dist(t,t-1)<δt-1)//判断质心距离是否小于阈值
7.iskeyframet←0;//若质心距离小于阈值则将标记置0
8.end if;
9.end if;
10.calculateδtusing Eq.(2);//更新阈值
11.return iskeyframet;
1.2 基于局部极值的指尖特征提取算法
手势指尖特征能够反映手势的结构特性,通过指尖特征的比较,可以区分具有相同运动轨迹但结构不同的动态手势。由于指尖处在手指的尖部,若将手指轮廓看作是一个光滑曲线,则指尖点就是该曲线上的局部极值点。因此,可以通过寻找手势轮廓上的局部极值点,确定手势中存在的指尖特征。
由于手势轮廓是一个连续的、多凹凸的曲线,很难构造出准确的函数表达式f来描述手势轮廓,因此无法通过求导的方式来确定曲线上的局部极值点。考虑到一根手指的指尖点与手势质心的距离应大于该手指上其他轮廓点与质心的距离,可以通过构造距离函数,确定手势中存在的指尖特征点。
定义1(手势指尖点):设第t帧手势图像轮廓点集为cst={ct,1,ct,2,…,ct,Nt},Nt为cst中轮廓点的个数。若存在一个ε>0,使得所有满足|ct,λ-ct,*|<ε的ct,λ,都有dist(ct,λ,gt)≤dist(ct,*,gt),则ct,*为一个手势指尖点。其中dist(ct,λ,gt)为距离函数,其表达式为:
(4)
其中,ct,λ=(xt,λ,yt,λ)为轮廓点ct,λ的坐标;gt=(xt,yt)为第t帧手势图像的质心坐标。
手势轮廓并非是一条理想的平滑曲线,轮廓上存在许多凹凸不平的点,仅通过距离计算与比较容易产生许多噪声特征点,降低指尖特征提取的准确性。此外,参数ε是影响指尖特征提取准确性的关键因素,若ε设置过大,则可能造成指尖特征点的丢失,相反则会产生许多噪声特征点。由于手势轮廓的凸包曲线是由手势最外层的轮廓点连接起来形成的凸多边形,手势的指尖特征必定处在手势的凸包曲线上,因此,可以利用手势的凸包曲线对得到的指尖特征点集进行过滤,只有满足手势指尖点的定义同时也处在凸包曲线上的特征点才认为是指尖特征点。
基于局部极值的指尖特征提取算法首先在手势轮廓上按顺序进行遍历,当某个轮廓点与质心的距离大于下一个轮廓点与质心的距离时,判断该点是否满足手势指尖点的定义,若满足,则认为该点为一个类指尖特征点;然后去除类指尖特征点集上所有在手势朝向上位置低于质心的特征点;最后计算手势的凸包,若类指尖点也处在手势的凸包曲线上,则认为该点为指尖特征点。
基于局部极值的指尖特征提取算法伪代码描述如下:
算法2:FingertipExtract(It)
输入:手势图像It
输出:手势指尖特征vt
1.max_dist←0;count←0;//初始化
2.cst←findcontours(It);//获取手势轮廓点集
3.hull←ConvexHull(It);//计算凸包
4.gt←CentroidCaculate(cst);//计算质心
5.forλ←0 to cst.length
6.calculate dist(cst,λ,gt) using Eq.(4);//计算与质心之间的距离
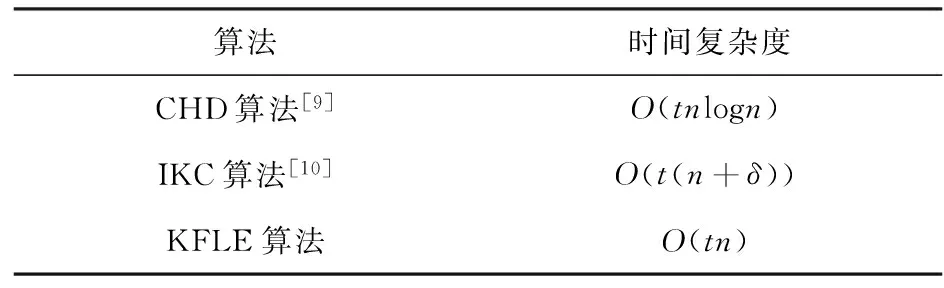
7.if(max_dist 8.max_dist=dist(cst,λ,gt); 9.fingertip←cst,λ; 10.count←0; 11.continue; 12.end if; 13.count←count+1; 14.if(count>ε&&fingertip.y>gt.y&&Exist(hull,fingertip))//过滤类指尖特征点 15.add fingertip tovt;//将fingertip添加到vt中 16.end if; 17.end for; KFLE算法包括两个步骤: (1)关键帧手势图像选取。首先计算当前帧手势图像的运动方向,若运动方向与前一帧手势图像的运动方向不同,则将该帧手势图像作为关键帧。否则计算相邻帧手势图像之间的质心距离,将距离大于阈值的手势图像作为关键帧。同时计算当前帧之前所有质心距离的平均值,更新阈值; (2)指尖检测和提取。将满足手势指尖点定义同时处在手势凸包曲线上的轮廓点作为指尖特征点。 KFLE算法的伪代码描述如下: 算法3:KFLE 输入:手势图像序列IInput={I1,I2,…,IN} 输出:手势特征向量VOutput={v1,v2,…,vM} 1.for eachItinIInput 2.isKeyFramet←KeyFrameSelect(It);//关键帧手势图像选取 3.if(isKeyFramet==0)//判断是否为关键帧手势图像 4.continue; 5.end if; 6.vt←FingertipExtract(It);//获取手势指尖特征 7.addvttoVOutput;//将vt添加到VOutput中 8.end for; KFLE算法的时间复杂度为O(tn),其中t为进行手势特征提取的次数,最坏情况下,t为动态手势序列的长度;由于在手势特征提取的过程中,需要对每个轮廓点进行计算,因此,基于局部极值的指尖特征提取算法的时间复杂度为O(n),n为手势轮廓点集的长度。表1比较了三种动态手势特征提取算法的时间复杂度。可以看出,KFLE算法具有较低的时间复杂度,可以缩短手势特征提取的时间。 表1 三种动态手势特征提取算法的时间复杂度 参照文献[15]的实验,文中共定义了十种动态手势类型,分别为单指向右、单指向下、二指向左、二指向上、三指向上、三指向右、四指向下、四指画圆、五指画圆、五指向左。每种手势类型由五名实验者各做2次,共得到100组动态手势视频。 与文献[9]提出的基于凸包缺陷的手势特征提取算法(简称为“CHD算法”)和文献[10]提出的基于改进k-曲率的手势特征提取算法(简称为“IKC”算法)进行对比。首先分析KFLE算法中关键参数数值的不同大小对手势特征提取准确性的影响,从而设置合适的关键参数数值。然后分别从手势特征提取处理时间和手势识别正确率两个方面评估各手势特征提取算法的性能。 实验的软硬件环境为:CPU:Intel(R) Core(TM) i5-4 210 M CPU@2.60 GHz;内存:8.00 GB;OS:Windows 8 Enterprise Professional 64 bit;摄像头:Integrated Camera;编程语言:C++;开发环境:OpenCV和Visual Studio 2013。 KFLE算法中的参数为范围阈值ε,ε的设置对指尖特征提取准确性具有较大的影响,参数设置过大或过小,都可能降低手势识别的准确性。为了分析和确定合适的ε,文中在相同的系统配置和实验环境下,首先为每个测试样本构造标准手势模板集,即运动轨迹相同,指尖个数分别为1~5,共五种动态手势类型;然后提取出在不同ε下的手势特征向量,特征向量包括每个关键帧手势图像的质心坐标和手势的指尖个数;最后采用动态时间弯曲(dynamic time warping,DTW)算法进行手势识别,并计算不同ε下的手势识别正确率,如图1所示。 图1 不同参数数值下的识别正确率 从图1可以看出,当范围阈值参数ε为10~30时,识别准确率较高,这是因为此时ε值能够在不丢失特征点的前提下,减少噪声特征点的出现。当ε设置过小时,可能会将凸包曲线上的其他数据点也作为指尖特征点进行提取,生成噪声特征点,降低手势识别的准确性。而当ε值设置过大时,可能造成即使是指尖点也很难满足手势指尖点的定义,导致指尖特征点的丢失。因此,ε的大小应选择在[10,30]范围内,文中实验设置ε=30。 在相同的系统配置和实验环境下,针对同一组动态手势视频,分别采用不同的动态手势特征提取算法进行特征提取,通过计算特征提取前后的时间差得到算法对该手势视频的特征提取时间,最后计算出每种算法对每种动态手势类型的平均特征提取时间,如图2所示。 图2 三种动态手势特征提取算法的平均特征提取时间 从图2中可以明显看出,与CHD算法和IKC算法相比,KFLE算法的平均特征提取时间分别降低了44.3%和71.9%。这是因为CHD算法和IKC算法需要对每一帧手势特性进行特征提取,而KFLE算法通过比较手势图像之间的运动方向和质心距离,仅对运动方向或距离发生明显改变的手势图像进行特征提取,减少了特征提取的次数。此外,在手势特征提取过程中,KFLE算法通过距离计算和凸包过滤,寻找手势轮廓曲线上的局部极值点,得到手势的指尖特征,降低了特征提取的时间复杂度,从而缩短了整个动态手势特征提取的时间。 将不同的手势特征提取算法提取出的特征向量采用DTW算法进行手势识别。实验采用留一交叉验证法,分别从每种手势类型的样本集中随机选择一组作为手势模板,将剩下的手势样本作为测试样本,对每种动态手势类型共进行100次测试,计算每种手势类型的识别正确率,如表2所示。 表2 各算法对不同手势类型的识别正确率 从表2可以看出,CHD算法的识别正确率明显低于IKC算法和KFLE算法,这是因为CHD算法通过比较手势中每个凸包缺陷的特征量之间的相互关系来判断是否存在指尖点,易受到噪声数据的干扰,因此识别正确率较低。而KFLE算法和IKC算法是通过对手势轮廓点的遍历和计算获得指尖点的位置信息,能够区分相似的手势类型,因此具有较高的识别正确率。 为了缩短动态手势特征提取的时间,提出一种基于关键帧和局部极值的动态手势特征提取算法。首先提出一种基于运动方向和自适应阈值的关键帧手势图像选取算法,通过比较相邻帧手势图像之间的运动方向和质心距离,选择运动方向或距离发生明显改变的手势图像进行特征提取。在对手势图像进行指尖特征提取的过程中,提出一种基于局部极值的指尖特征提取算法,通过构造距离函数并结合凸包过滤,寻找手势轮廓曲线上的局部极值点,确定手势中存在的指尖特征。 该手势特征提取算法对手势交互的环境具有较高的要求,在复杂背景和光照效果较差的环境下,会降低手势特征提取的准确性。因此,下一步将对在复杂环境下的手势特征提取算法进行研究,增加算法的实用性和健壮性。 [1] LIU Y,YIN Y,ZHANG S.Hand gesture recognition based on HU moments in interaction of virtual reality[C]//Proceedings of 2012 4th international conference on intelligent human-machine systems and cybernetics.Washington,DC,USA:IEEE Computer Society,2012:145-148. [2] LIN J,DING Y.A temporal hand gesture recognition system based on hog and motion trajectory[J].International Journal for Light and Electron Optics,2013,124(24):6795-6798. [4] 张墨逸,张秋余,芦俊池,等.基于结构特征点的手势建模与高层特征提取[J].华中科技大学学报:自然科学版,2015,43(10):87-91. [5] NAGARAJAN S,SUBASHINI T S,RAMALINGAM V.Vision based real time finger counter for hand gesture recognition[J].International Journal of Technology,2012,2(2):1-5. [6] 冯志全,杨 波,郑艳伟,等.基于特征点分布分析的手势 特征检测方法[J].计算机集成制造系统,2011,17(11):2333-2342. [7] HASAN M M,MISHRA P K,MISHRA P K.Real time fingers and palm locating using dynamic circle templates[J].International Journal of Computer Applications,2012,41(6):33-34. [8] HUANG H,JU Z,LIU H.Real-time hand gesture feature extraction using depth data[C]//2014 international conference on machine learning and cybernetics.[s.l.]:IEEE,2014:206-213. [9] GANAPATHYRAJU S. Hand gesture recognition using convexity hull defects to control an industrial robot[C]//2013 3rd international conference on instrumentation control and automation.[s.l.]:IEEE,2013:63-67. [10] 李博男,林 凡.基于曲率的指尖检测方法[J].南京航空航天大学学报,2012,44(4):587-591. [11] PATHAK B,JALAL A S,AGRAWAL S C,et al.A framework for dynamic hand gesture recognition using key frames extraction[C]//2015 fifth national conference on computer vision,pattern recognition,image processing and graphics.[s.l.]:IEEE,2015:1-4. [12] TAN W,WU C,ZHAO S,et al.Dynamic hand gesture recognition using motion trajectories and key frames[C]//2010 2nd international conference on advanced computer control.[s.l.]:IEEE,2010:163-167. [13] 曹昕燕,赵继印,李 敏.基于肤色和运动检测技术的单目视觉手势分割[J].湖南大学学报:自然科学版,2011,38(1):78-83. [14] 王小俊,刘旭敏,关 永.基于改进Canny算子的图像边缘检测算法[J].计算机工程,2012,38(14):196-198. [15] 王西颖,戴国忠,张习文,等.基于HMM-FNN模型的复杂动态手势识别[J].软件学报,2008,19(9):2302-2312.1.3 算法描述和时间复杂度分析
2 实验结果与分析
2.1 实验环境及参数设置
2.2 KFLE算法中关键参数的设置
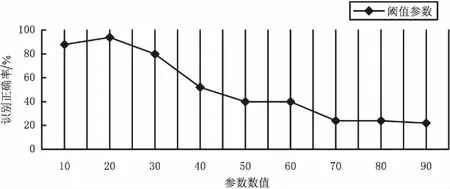
2.3 手势特征提取时间的比较
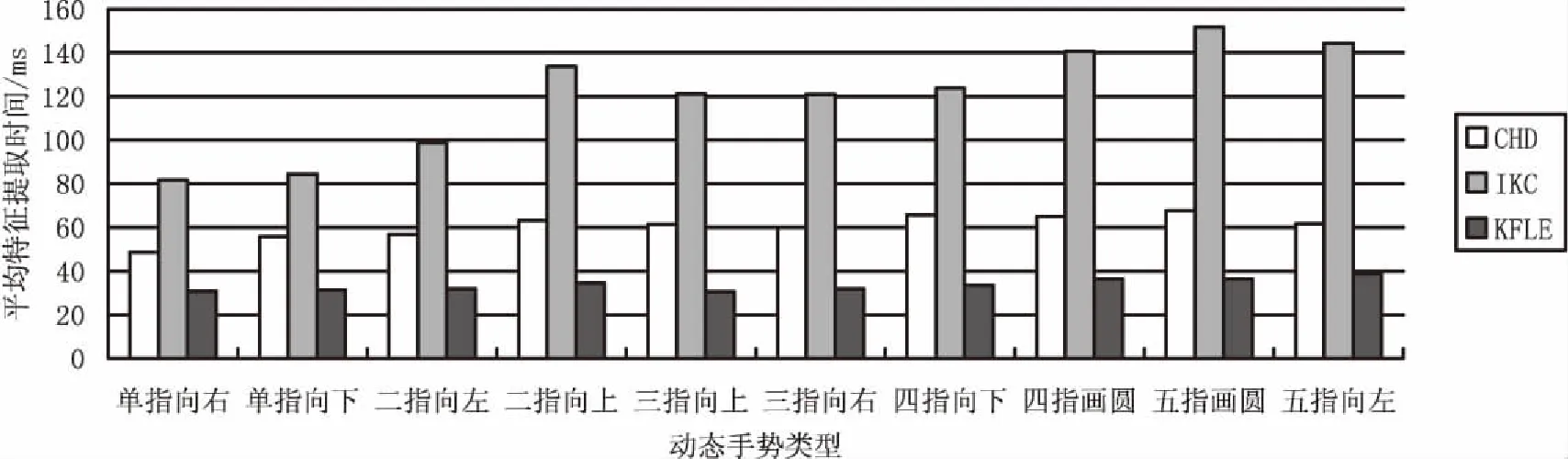
2.4 手势识别正确率的比较
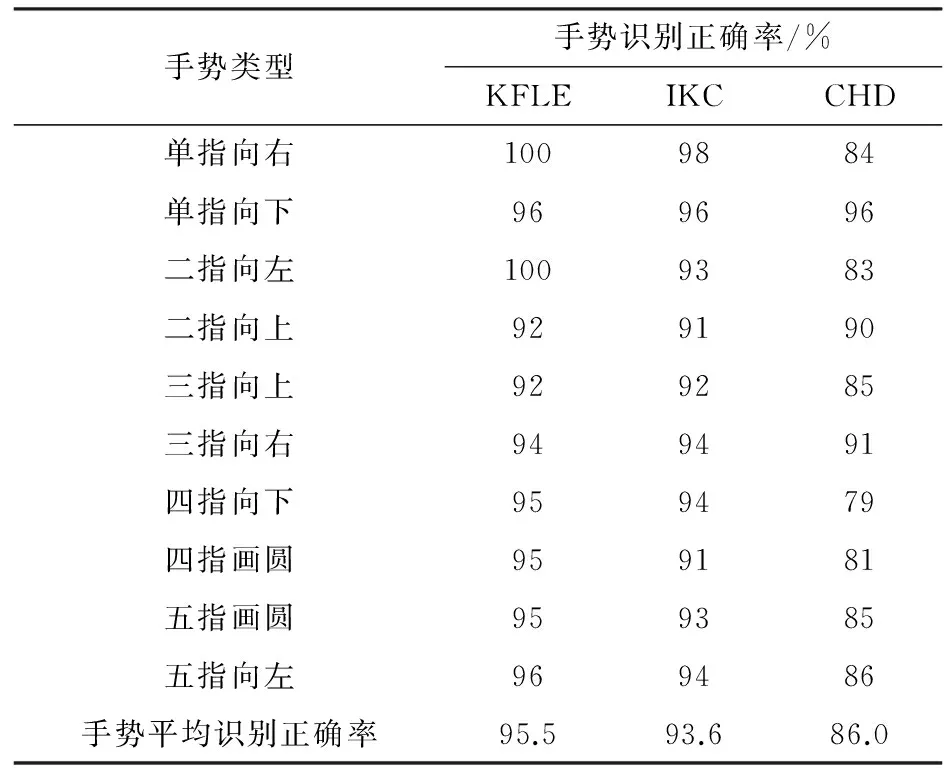
3 结束语
