基于系数复用和字典训练的图像超分辨率算法

史国川，龚连友

(陆军军官学院 计算中心，安徽 合肥 230031)

0 引 言

作为数字图像处理领域的热点之一，图像的超分辨率[1-2](super resolution，SR)重建一直是广大研究者的重点研究方向。由于目前软硬件等条件的限制，得到的图像分辨率难以满足实际应用中的要求，这就需要对低分辨率图像进行SR重建以此来提高图像的分辨率。Freeman等[3]提出的基于实例进行字典训练的重建算法是其中的经典算法。该算法通过对图像块进行约束，建立高低分辨率图像块间的对应关系，但是该过程需要训练的数据量大、耗时长，而且在重建过程中还需要大量时间对数据库进行搜索匹配，因此该算法效率不高。Yang等[4]利用稀疏表示对图像进行SR重建。该算法首先对图像进行稀疏表示，然后选择一组特定的稀疏基，使得不同分辨率的图像块能用相同的稀疏表示对其进行描述。该算法明显降低了算法重建过程中的耗时，并且重构图像的分辨率得到了提高；但是没有对字典训练过程进行优化，因此在字典训练阶段仍需大量时间。奇异值分解[5](K-SVD)作为图像SR重建领域经典的字典训练算法之一，因其较好的重建结果，自提出以来得到了广泛的应用。但是K-SVD算法存在字典训练耗时长，重建恢复的图像分辨率不高等缺点。Leslie等[6]提出一种改进的复合字典训练和系数复用算法，但并没有将其应用到图像的超分辨率重建中。

在上述研究的基础上，文中提出一种基于系数复用和稀疏表示[7-14]的改进K-SVD字典训练算法，在图像的稀疏表示以及字典更新过程中对算法进行优化改进，在明显降低算法耗时的同时进一步提高了重建超分辨率图像的质量。

1 基于稀疏表示的图像超分辨率重建算法

研究表明，可以通过对一幅高分辨率(HR)图像进行下采样和模糊处理来获取其低分辨率(LR)图像。当使用狄拉克函数δ作为模糊核时，直接对HR图像进行下采样处理即可得到其低分辨率图像，而不用再进行模糊处理，因此，可以将超分辨率重建问题转化为图像插值问题。作为一个典型的逆向问题，图像超分辨率重建可以用如下公式进行描述：

y=SBx+v

(1)

其中，x表示原始HR图像；B表示模糊算子；S表示下采样算子；v表示添加的噪声；y表示已获的LR图像。

将B定义为一个矩阵，同时令v=0，代入式(1)中有y=Sx，因此可以认为y是通过对x进行下采样得到的。

通过式(1)对x进行重建是一个非唯一解的逆向问题，在稀疏表示过程中，假定在利用字典(D)约束后图像在某些域内是稀疏的，即在公式x≈Dα中，矩阵α中的绝大多数元素都是接近于0的。因而稀疏表示的正则化矩阵[15-16]可以表示为R(x)=‖α‖0。由于求解过程是非凸的，最优化的稀疏表示结果难以得到，可以采用凸处理对其进行近似求解，公式如下：

(2)

由于求解α过程只考虑了低分辨率情况，而图像SR重建需要确定高低分辨率图像在高低分辨率过完备字典的相同稀疏表示，因此DCT就成为利用稀疏表示进行图像SR重建的重要内容。

2 K-SVD字典训练算法

K-SVD算法最先由Aharon[5]等提出，该算法在确保不丢失初始字典所有信息的条件下有效减少了生成的过完备字典[15-16](DCT)中原子的数量。

字典训练实际上是对一个问题进行优化求解，可以用公式表示如下：

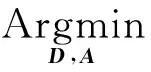
‖αi‖0≤t0

(3)

在接收到输入信号之后，开始进行字典训练，在训练过程中，需要确定过完备字典D与其稀疏表示A。但是，在实际操作中对两个未知参数同时进行优化求解是非常复杂的，因此假设已经确定了字典D，式(3)的优化问题就可以转化成求解训练样本集合X的稀疏表示矩阵A，然后利用Aharon提出的追踪算法确定稀疏表示的分解因子。

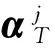
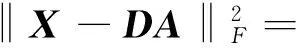
(4)

(5)

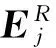
3 改进的K-SVD算法

3.1 对字典更新阶段的改进

(6)

由于矩阵AAT规模庞大，用常规方法求解计算量大，耗时长，而利用XAT=DAAT对其进行迭代求解，在明显减小迭代次数的同时可以得到一个理想的近似解。需要注意的是，K-SVD算法不仅对D中的原子进行了更新，而且将A中所有不为0的系数与之相乘。因此，K-SVD在字典更新阶段对D和A同时进行了更新。根据K-SVD算法的特点，改进算法的目的是在保证A的完整性条件下找到同时对D和A进行更新的方法，根据式(7)对D和A进行优化。

(7)

在满足条件A⊗M=0的同时还要保证A中所有0系数的完整性，其中A⊗M表示两个相同大小矩阵之间的乘法，M表示只含0、1元素的掩码矩阵，M={|A|=0}，其值由式(8)确定。

(8)

求解过完备字典是一个非凸问题，直接计算难度较大。首先，将DA分解成秩为1的矩阵之和，然后代入式(7)中得到：

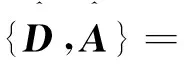
n,mj⊗αj=0

(9)

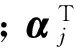
基于式(10)中的SVD矩阵，采用块坐标下降法对(dj,αj),j=1,2,…,n进行逐项优化。

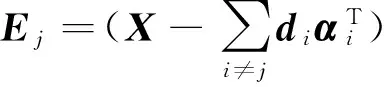
(10)

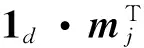
传统K-SVD字典训练算法通常只进行一次(j=1,2,…,n)字典更新计算，而改进算法为了获得更接近式(7)所描述的整体解决方案，会进行多次(j=1,2,…,n)更新计算。

尽管改进算法在某种程度上增加了计算复杂度，但是这种新增的复杂度在整个字典更新过程中几乎可以忽略不计，这是因为在绝大多数情况下，字典训练的计算量集中于稀疏编码阶段，即表明所增加的额外计算量在整体运行时几乎保持不变，因此改进前后的K-SVD算法在计算复杂度方面基本相等。

3.2 正交匹配追踪中的系数复用

假设给定一个已经更新的字典，K-SVD算法能够对其进行搜索，然后根据得到的稀疏表示结果对数据进行训练。如果选择先前计算的表示，使目标函数保持在相同的高度。这表明，可以使用给定的表示，作为追踪阶段的良好开始，然而，这并不意味着能够改进结果。

利用该方法对追踪算法中的系数进行初始化时，可能会陷入各种松弛或贪心的稀疏编码[17-18]方法中。文中专注于贪心追踪算法中一个特定的变量，它建立在CoSaMP[10]和Subspace Pursuit[11]的追踪算法之上，与这些方法不同的是，改进算法中有k/3个最大系数的初始值来自于前期的追踪阶段，然后像CoSaMP和SP算法一样进行一个系数增大和修剪的过程，这就是正交匹配追踪中的系数复用算法(CoefROMP)。

CoefROMP算法流程如下：

输入：D，x，α0(初始值)和k(目标基数)。

初始化(n=0)：从α0中取最大的k/3个元素，T0:=(|α0|,k/3)；r0:=x-DT0αT0；ε0:=‖r0‖2。

从n=1开始进行如下迭代计算，直到达到最大迭代次数结束循环：

(1)从预计剩余中取值最大的k/3个元素，Sn:=(|DTrn-1|,k/3)；

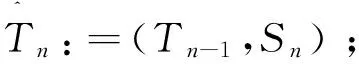
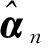
(5)更新稀疏表示：αn:=(DTn)+x；

(6)更新剩余值：rn:=x-DTnαn，εn:=‖rn‖2；

(7)当满足条件εn>εn-1时，退出循环。

输出：更新后的稀疏表示α。

4 实验结果与分析

4.1 字典更新阶段

实验中选择了一组被广泛用于字典训练的图片集合作为标准图像库，从这些图片中提取50 000个图像块用于训练更新。减去所有图像块的平均值，用以消除需要使用的数据矢量的常数偏移系数，稀疏表示的质量高低取决于字典中原子的数目n和其中的非0系数数量k。假设信号的维度为d，那么有n=3d，k=round(d/10)，同时，利用训练样本得到的数据对字典进行初始化。

实验在Matlab R2014a，CUP为双核2.3 GHz，内存为4 GB，操作系统为Windows7的手提计算机上进行。将传统的K-SVD作为基准算法，采用8×8的图像块(d=64)和64×192大小的字典，因此，稀疏表示基数k=6。通过图1可知，训练数据可以从几次更新周期中获益，并且每一个更新周期计算成本小；另外，大部分的增益发生在前几次迭代过程中。

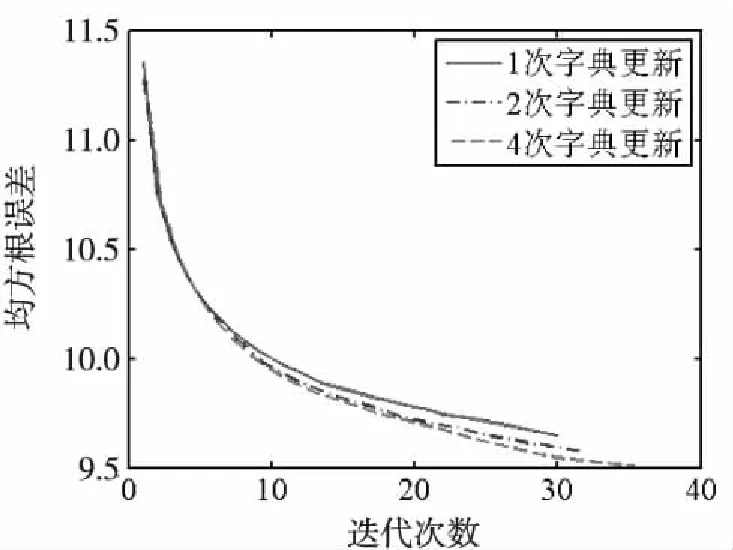
图1 不同次数字典更新对比

4.2 系数复用阶段

将传统正交匹配追踪算法与改进后的正交匹配追踪算法进行比较。实验中，仍然选择50 000个图像块用于字典训练，利用15×15大小的图像块进行实验，因此与之对应的向量长度为225，被训练的字典大小为225×675，稀疏表示基数k=23。实验结果如图2所示。分析图2可知，与传统的OMP[12]算法相比，CoefROMP算法在降低均方根误差和计算耗时方面有明显的提高。

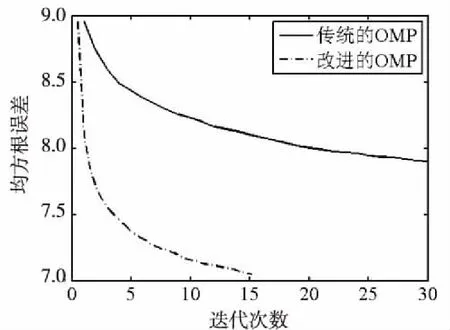
图2 两种正交匹配追踪对比

4.3 重建结果比较

实验以双三次插值算法为基准，对改进后的K-SVD算法与传统K-SVD的实验结果进行比较，判断三种重建算法的优劣。在三种重建算法的基本参数与字典训练过程均相同的情况下，其中图像块数量为50 000个，字典大小为64×192，分别使用标准图像中Raccoon(109×100)、Girl(85×86)和Flower(110×57)图像进行重建实验，结果如图3～5所示。

图3 三种算法的重建结果比较(Raccoon)

图4 三种算法的重建结果比较(Girl)

根据图3～5的观察，并将三种算法所得结果与原始高分辨率图像对比可知，在三种重建算法中，文中算法在Raccoon的毛皮、Girl鼻翼的雀斑以及Flower的叶茎等细节上具有更好的表现，重建获得的图像质量最高，与原高分辨率图像最为接近，说明改进后的K-SVD算法是最优的。

图5 三种算法的重建结果比较(Flower)

5 结束语

通过对基于稀疏表示的经典K-SVD字典训练算法中字典更新阶段的改进，结合正交匹配追踪中的系数复用算法，设计了一种新的超分辨率重建算法。该算法极大地降低了重建过程中字典训练所消耗的时间，只需几分钟对原有的字典进行更新即可。将新算法得到的字典采用稀疏表示对不同图像进行超分辨率重建，提高了重建图像的质量。

[1] 苏 衡，周 杰，张志浩.超分辨率图像重建方法综述[J].自动化学报,2013,39(8):1202-1213.

[2] YANG J,LIN Z,COHEN S.Fast image super-resolution based on in-place example regression[C]//Computer vision and pattern recognition.Washington,DC,USA:IEEE Computer Society,2013:1059-1066.

[3] FREEMAN W T,PASZTOR E C,CARMICHAEL O T.Example-based super resolution[J].IEEE Computer Graphics and Applications,2002,22(2):56-65.

[4] YANG J,WRIGHT J,HUANG T,et al.Image super-resolution via sparse representation[J].IEEE Transactions on Image Processing,2010,19(11):2861-2873.

[5] AHARON M,ELAD M,BRUCKSTEIN A.K-SVD:an algorithm for designing of complete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing,2006,54(11):4311-4322.

[6] LESLIE N S,ELAD M.Improving dictionary learning:multiple dictionary updates and coefficient reuse[J].IEEE Signal Processing Letters,2013,20(1):79-82.

[7] 张 瑞,冯象初,王斯琪,等.基于稀疏梯度场的非局部图像去噪算法[J].自动化学报,2015,41(9):1542-1552.

[8] 徐国明,薛模根,崔怀超.基于过完备字典的鲁棒性单幅图像超分辨率重建模型及算法[J].计算机辅助设计与图形学学报,2012,24(12):1599-1605.

[9] 徐国明,薛模根,袁广林.基于混合高斯稀疏编码的图像超分辨率重建方法[J].光电工程,2013,40(3):94-101.

[10] NEEDELL D,TROPP J A.CoSAMP:iterative signal recov-

ery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis,2008,26:301-321.

[11] DAI D,MILENKOVIC O.Subspace pursuit for compressive sensing[J].IEEE Transactions on Information Theory,2009,55(5):2230-2249.

[12] 李少东,裴文炯,杨 军,等.贝叶斯模型下的OMP重构算法及应用[J].系统工程与电子技术,2015,37(2):246-252.

[13] LIU D,WANG Z,WEN B,et al.Robust single image super-resolution via deep networks with sparse prior[J].IEEE Transactions on Image Processing,2016,25(7):3194-3207.

[14] TIMOFTE R,DE V,GOOL L V.Anchored neighborhood regression for fast example-based super-resolution[C]//IEEE international conference on computer vision.Washington,DC,USA:IEEE Computer Society,2013:1920-1927.

[15] 李 娟,吴 谨,陈振学,等.基于自学习的稀疏正则化图像超分辨率方法[J].仪器仪表学报,2015,36(1):194-200.

[16] 孙玉宝,费 选,韦志辉,等.基于前向后向算子分裂的稀疏性正则化图像超分辨率算法[J].自动化学报,2010,36(9):1232-1238.

[17] 沈 辉,袁晓彤,刘青山.基于预测稀疏编码的快速单幅图像超分辨率重建[J].计算机应用,2015,35(6):1749-1752.

[18] 潘宗序,禹 晶,肖创柏,等.基于自适应多字典学习的单幅图像超分辨率算法[J].电子学报,2015,43(2):209-216.