基于模场自积增强检测的光纤声光旋转传感器∗

2018-03-19刘昱任国斌靳文星吴越杨宇光简水生

物理学报 2018年1期

刘昱任国斌靳文星吴越杨宇光简水生

1)(北京交通大学,全光网络与现代通信网教育部重点实验室,北京 100044)

2)(北京交通大学光波技术研究所,北京 100044)

1 引言

旋转传感器是建筑物结构健康监测[1,2]和危险环境偏移预警[3,4]中的重要传感系统.光纤旋转传感器有抗电磁干扰、结构体积小、易于长距离传输和可埋设入物体内部的优点,近年来被广泛研究.常用的光纤旋转传感器主要利用环境的物理旋转对光纤中传输光波长的扰动原理进行旋转感知,比如基于光纤光栅的结构[5,6]、基于光纤干涉器的结构[7,8]、基于Sagnac效应[9,10]、基于光子晶体光纤[11]的结构和基于光纤偏振器的结构[12,13].由于旋转参量的形状对称性,所以传统基于光谱偏移测试法的光纤传感器能够感知到旋转角度的变化,但难以分辨旋转顺、逆时针方向的变化.从传感接收端的角度看,上述的基于光谱偏移测试法的光纤传感器具有精度高、测试重复性强的优点.但是由于需要检测光波长偏移与强度扰动,这些光纤旋转传感器全部依赖于对波长改变的监控,这意味着这些传感器需要包含光谱仪(optical spectrum analyzer,OSA),而光谱仪的较高成本和对温湿度敏感的特点增加了整个系统的造价和适用环境的范围.另一方面,基于光栅和干涉结构的光纤传感器存在着轴向应力与旋转应力的交叉敏感性、温度与旋转角度的交叉敏感性.为了解决交叉敏感性的问题,可以采用复频谱分析来分辨不同参量对光谱的影响,而这需要更高精度的光谱仪;也可以采用特殊设计的光子晶体光纤和光栅来分离或者减轻交叉敏感性.由于波长偏移的范围限制和光谱仪测试速度的限制,传统基于光谱偏移测试法的光纤传感器难以进行长时间与动态旋转角度的监控.

最近提出了一类基于光学模场变化监测的光纤传感器,以图像强度检测器来监控光纤中光学模场随环境传感量的变化,从而测量被传感对象.比如用图像接收器测量光学杠杆中模场位置变化来监测物体位移[14]、用图像接收器测量光模场传输距离来监测人体表面位移[15],将光纤干涉现象转化为模场输出干涉图像条纹来监测光纤曲率的变化[16]、用强度传感器接收的模式耦合输出变化来监测光纤扭曲[17].基于光学模场变化监测的传感器的最大特点在于用图像检测器替代了传统光纤传感器中的频谱测量仪器,从而使整个传感系统接收端结构简化、成本降低并能直观表达出被测物的变化、记录动态时域传感过程.在基于光学模场变化监测的光纤传感器中采用何种动态图像处理技术决定着整个检测端的检测精度和效率的高低.传统的图像识别技术对光学模场的监测步骤通常包含图像分割、形状特征提取和特征识别三个步骤[18−20],其中形状特征提取最关键、占用的计算时间最长、也具有较大的计算复杂度.

本文提出一种结构简单、传感计算速度快的基于模场自积增强检测的光纤声光旋转传感器.用微波调制的压电陶瓷(piezoelectric ceramic transducer,PZT)与少模光纤制成的光纤声致光栅(acoustically-induced fi ber grating,AIFG)输出非圆对称LP11模式,再将LP11模式传输至由少模光纤构成的传感头上,使得输出光模场会随着环境的旋转而旋转,最后由电荷耦合元件(charge-coupled device,CCD)接收处理光模场图像,计算出动态旋转方向与角度.为了提高传感器计算精度与速度,提出了专门适用于光纤模场的自积增强算法进行图像处理,其不仅只需要特征提取和特征识别两步计算,还将特征提取的算法复杂度大大降低.最后实验验证了此旋转传感系统可以进行0°—180°的全角度测量,旋转角度测量误差小于11%.并且在传输路径上100—1500µε环境下应力不敏感.

2 传感器的结构和实验原理

2.1 传感系统的实验结构

图1给出了基于模场自积增强检测的光纤声光旋转传感器的结构示意图.法布里-珀罗二极管激光器(Fabry-Perot laser diode,FPLD)为光源直接以普通单模光纤输出,其输出中心波长在1542 nm.光源输出的普通单模光纤直接与我们实验室的改良化学气相沉积法制作出的双模光纤熔接耦合.其中双模光纤芯子直径为12.3µm,包层直径110µm,芯子与包层折射率差为5.4‰,这样模场面积略大于单模光纤的少模光纤可以以低耦合损耗的代价接收只有基模的传感光,并在双模光纤中激发出LP01和LP11模式.将一段腐蚀至包层直径44µm的双模光纤以紫外胶黏贴的方式直接附着于声光调制器上,其中声光调制器由微波可调压电陶瓷和树脂锥尖构成.当微波发生器发出微波调制压电陶瓷,压电陶瓷会产生声致震动并由树脂锥尖传输到被腐蚀的双模光纤中,双模光纤会因上下振动而产生横向弯曲声波,从而使得声光耦合区域的光纤在垂直与轴向上的周期性微弯,折射率分布也将发生变化而产生声致光栅.声致光栅在特定频率的微波下将1542 nm附近的LP01模滤掉保留LP11模式.接着声致光栅连接着双模光纤将LP11模式输出,并由微透镜聚焦校准,这段双模光纤为传感头会随着旋转平台的转动而转动.然后输出的LP11传感模式由CCD接收,CCD将传感模场分布转化为数字信号传输给图像处理器以自积增强检测算法计算出光纤旋转角度.

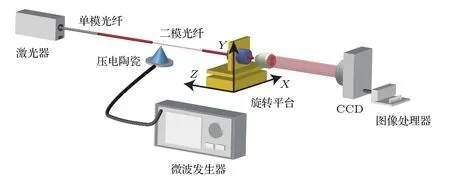
图1 光纤旋转传感器的实验装置图Fig.1.Experimental setup for fi ber torsion sensor.

2.2 光纤声光光栅传输特性原理

本文所述传感器中的光纤声光光栅主要由压电陶瓷和双模光纤组成.微波发生器发出的特定频率的微波信号加载到压电陶瓷上时,压电陶瓷会产生声波,声波会被压电陶瓷上附着的锥尖放大并传输至被腐蚀的双模光纤中.周期性声致振动将在双模光纤中形成折射率调制,形成类似于长周期光纤光栅的光纤声致光栅.其中光纤声致光栅中折射率调制会影响光纤中芯模和包层模之间的耦合,从而形成在特定波段中特定芯模被耦合到包层模,也就是在特定波段中特定芯模被损耗掉.其中光纤声致光栅的相位匹配条件为[21,22]

其中n0是光纤芯子的折射率,∆n(x,y)是声致折射率调制深度,ψ1(x,y)是LP01模式的模场分布,ψ2(x,y)是LP11模式的模场分布.微波激发的声致折射率调制是模式与模式之间耦合的关键,在被腐蚀光纤中由声波引起的介电常数扰动表现在折射率上为[21,22]

其中χ=−0.22是光纤的弹光系数,κ是声波波矢,u0是声波波幅.光纤声致光栅被视为一种光纤模式转换器,并不直接参与传感而是产生传感所需的LP11模式.为了方便调节加载在压电陶瓷上的微波频率,我们单独建立了一套传输光谱测试系统,用于测试光纤声致光栅的输出光谱.用宽带白光光源(white light laser)作为输入光引进双模光纤,再将双模光纤与光纤声致光栅耦合,最后光纤声致光栅输出端一部分单模光纤耦合至光谱仪观察传输损耗谱,一部分耦合至CCD观察模场变化.如图2所示,白光光源的传输谱在1500—1560 nm之间是比较平坦的,而白光光源经过加载952.3 kHz微波的光纤声致光栅的输出谱在1542 nm附近损耗接近10 dB,这说明在1542 nm附近光纤声致光栅将传输光的90%的LP01模式转化为LP11模式了.白光光源本身的LP01模式输出是圆对称的模场分布,而经过加载952.3 kHz微波的光纤声致光栅输出的LP11模式是分瓣的非圆对称模场分布.

图2 光纤声致光栅的基模损耗谱Fig.2.Transmission spectra of the AIFG.

2.3 模场自积增强检测算法

最基本的圆对称模式(比如LP01模)因其旋转对称性是无法感知角度变化的,只有非圆对称模式(比如LP11模)才能感知旋转中的角度变化.而LP11模的非圆对称性依然不够强,所以常规方法是给予特征学习从形状变化读取的角度来检测模场的转动.我们搭建的光纤声光旋转传感器中采用模场自积增强算法,这种算法增强了模场图像的非圆对称性,从而能轻易在识别过程中读取模场的角度变化.模场自积增强算法主要由自积增强特征提取和特征识别两个步骤构成.这里提出的模场自积增强检测算法中放弃了传统图像识别的基于图像形状特征的检测步骤,这样将算法复杂度大大降低;由于不计算图像的形状,所以仅靠图像本身未处理的信息无法用于动态变化检测.故我们对图像进行自积增强,使得图像的特征变化极大地加强,以便于之后动态检测的计算.

为了得到最初的图像模场分布矩阵,从模场接收器CCD中读取光学模场分布如图3(a)所示,并在数据处理器中转换为灰度归一化数值矩阵A=A(M,N)如图3(b)所示,其中取值为0的点代表此处模场光强为0,取值为1的点代表此处模场光强为接收器最大检测功率,m和n代表垂直于光纤模场传输方向的xy平面.然后将模场分布矩阵Amn代入到k阶自积增强函数fk得到模场自积值：

其中fk,n是Amn在x方向上的自积值,fk,m是Amn在y方向上的自积值.由上可知整个矩阵自积增强过程是由图3(c)所示的矩阵自增强分布

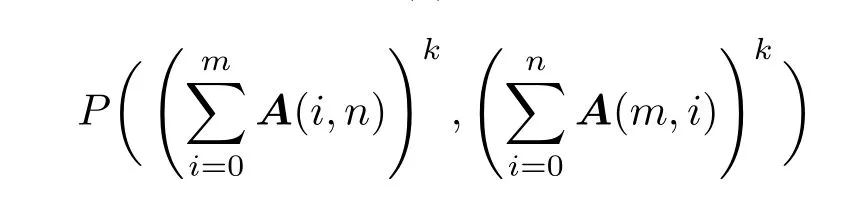
图3 自积增强算法的步骤 (a)CCD读取的模场图像;(b)灰度化后的模场图像;(c)模场图像的自积分布;(d)对模场图像的自积分布做积分Fig.3.The steps of enhanced self-integration algorithm:(a)Using CCD to read the fi eld image;(b)gray fi eld image;(c)self-integration distribution of fi eld image;(d)integration of self-integration distribution of fi eld image.

和图3(d)所示的矩阵自积分布B(fk,n·fk,m)组成.由图3可知,自积增强的物理意义在于将模场分布矩阵Amn模进行自增强,再在所对应的垂直方向进行自压缩,这样增强与压缩并存的计算过程能很大程度地将模场分布的特征收集到自增强分布

中,然后为了减少之后的特征识别步骤的算法复杂度,进一步对自增强分布积分得到

接着在旋转模场特征提取的过程中,将初始模场分布矩阵A按θ度数旋转得到Aθ

其中θ为模场旋转角度取0到π,m′指的是x方向上旋转后的坐标,n′指的是y方向上旋转后的坐标.然后将旋转后的模场分布Aθ代入到自积分布B(fk,n·fk,m)得到0°—180°旋转模场自积值:

其中值得注意的是旋转模场自积分布fθ,n和fθ,m都是二维分布,x轴是模场旋转角度θ,y轴是模场自积值.由于k阶自积分布函数fk仅仅只对单轴上的纵向做了一遍相加次基本计算),一遍平方(1次基本计算)和单轴上横向一遍相加次基本计算),算上x和y双轴总共次2n级别基本运算不像传统的光学图像识别需要将每个特征点(n次运算)对全局(n次运算)进行特征分析(总共n2级别运算),这里用到的自积增强特征提取的时间复杂度大大降低.

在传感检测过程中,传输到处理器的光学模场图像先通过自积增强函数得到自积值x和y方向的测试自积值反向代入到基于旋转角度的模场自积值fθ,m和fθ,n中就能得到光学模场的旋转角度.这里设定为角度α到角度β之间的分辨比例,为0°—180°之间的分辨比例,代表系统探测出多少度的旋转需要自积值变化百分之多少.意味着分辨比例H越大,这个系统的特征识别能力越强;反之分辨比例H如果很小,表明此系统中模场大角度与小角度旋转的自积值差别很小,难以分辨.

3 实验系统及测量结果

在搭建好的光纤声光旋转传感器中,将952.3 kHz微波加载到PZT上使得生成的光纤声致光栅能刚好在输入1542 nm激光波长范围中将光模式转化为LP11模.将LP11模输出至自制双模光纤当作并传感头,传感光空间传输至CCD并经处理器运算计算出旋转方向和角度.首先将旋转平台角度调至平衡并对双模光纤输出的LP11传感模式进行角度校准.当CCD接收到初始的非圆对称模场后开始执行特征学习,将模场分布数据导入到处理器,处理器利用旋转矩阵得出0°—180°模场,代入自积增强函数得到随角度变化的自积特征分布Aθ.如图4,在同时支持LP11模式和LP11模式的双模光纤中调节声致光栅的滤波深度能得到不同的输出模场分布,其中只有LP11模式能被用于角度传感.激发出更纯的LP11模式和屏蔽LP01模式是系统传感光实现的关键,从图4(f)中可以看出,总模场分布中占90%功率的LP11模式形成双瓣分离模斑,占10%功率的LP01模式形成隐约可见的圆形模斑.在模场自积增强检测的灰度化模场图像这一步中(见2.3节),模糊的LP01模斑被连同背景去掉,理论上小于20%总功率的LP01模斑对最后计算旋转角度的影响极小.

如图5,当k=1时,一阶自积增强函数只是读取数据并对矩阵积分,没有对模场特征增强.从图5(a)可以看出,自积分布B在各个角度幅度都相似,自积特征分布Aθ混乱且不连续,分辨比例只有H=2.994×105−2.978×105/2.978×105=0.54%;而且图5(b)其中随角度变化自积值的微小变化只是由旋转矩阵中的像素计算误差造成的,无法进行角度变化的识别.

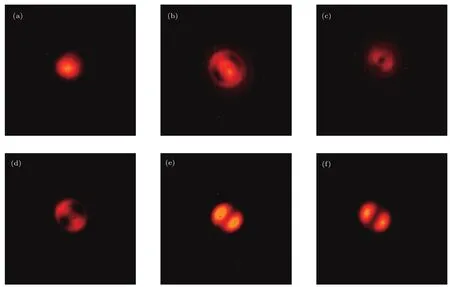
图4 CCD接收的输出模场分布图 (a)滤波深度0 dB;(b)滤波深度2 dB;(c)滤波深度4 dB;(d)滤波深度6 dB;(e)滤波深度8 dB;(f)滤波深度10 dBFig.4.CCD output of the mode fi eld distribution when the fi lter depth is(a)0 dB,(b)2 dB,(c)4 dB,(d)6 dB,(e)8 dB and(f)10 dB.

图5 LP11模式随角度旋转的一阶自积分布与自积值 (a)沿x轴的一阶自积分布与自积值;(b)沿x轴的自积值Fig.5.First order self-integration and the distribution of self-integration in LP11mode with different angles:(a)First order self-integration and the distribution of self-integration along x-axis;(b) fi rst order self-integration along x-axis.

如图6,分别采用了二阶自积增强函数和三阶自积增强函数.为了直观地表达出特征学习过程,图6展示了在对应的模场旋转角度下输出对应的自积分布B,以及每个对应的自积分布B连续输出的自积特征分布Aθ.从图6(a)中可以看出,在采用了二阶自积增强函数后,自积分布B表达出了LP11模场在角度随变化增大,x轴映射的图像从初始的分瓣到合瓣再到最终分瓣,每个角度的自积分布B有了明显区分,并且自积特征分布Aθ平稳连续,适合用于识别角度变化.图6(b)中所有图像都旋转了90°,用于分析y轴映射的函数分布,可以看出y轴映射的自积分布B的变化趋势与x轴映射的相反,从初始的合瓣到分瓣再到最终合瓣.图6(c)表达了经历整个特征学习过程后获取的x轴与y轴的自积特征分布Aθ,可以看出在二阶自积增强后x轴和y轴分辨比例达到H=2.85×109−1.83×109/1.83×109=56%远高于没有自积增强的分布.

确定LP11模的自积特征分布后,当旋转平台牵动光纤旋转时引起CCD接收模场变化,只需要把变化后的图像代入自积增强函数将得出的x轴与y轴的自积值与自积特征分布比对就能得出旋转角度.图6(d)—(f)为当k=3时模场经过三阶自积增强学习后得出的特征模型,可以看出特征分布形状和二阶相似但每个角度的特征区别更大,x轴和y轴分辨比例达到H=2.84×1013−1.16×1013/1.16×1013=145%,比二阶特征增强函数更能识别出小角度变化.测量角度的实验中没有用一阶自积增强函数是因为一阶自积增强函数只是读取数据并对矩阵积分,没有对模场特征增强的作用,无法进行角度变化的识别.

如图7,在将旋转平台的旋转角度定义为标准角度(即旋转平台的旋转角度误差为0)的条件下,我们测试了10次旋转平台以每秒1°的旋转速度从0°到180°旋转中传感系统对角度测量的误差百分比,给出传感系统在不同角度下的误差范围与平均误差.测试结果中不同角度区间下误差不同主要原因有两个:一是因为我们研制的双模光纤输出的LP11模场不是上下对称,导致非圆对称模随角度变化的规律在0°—90°与90°—180°也不一致;二是因为算法本身的分辨比例影响了识别精度,双瓣分得越开的部分越精确.实验中采用二阶增强算法和三阶增强算法分别能使最大测量误差范围(单一角度下正向偏差最大值与负向偏差最大值之差的绝对值)小于28%和小于11%.从图7(a)中看出,在45°与135°附近最大测量误差范围较大,达到24%,这是因为模场分布旋转时在x轴和y轴上的映射由正切函数得出,而正切函数在45°与135°时非常敏感,所以导致测量偏差较大.从图7(b)中可以看出,用三阶自积增强算法比用二阶增强算法的误差浮动小一些,特别是在45°与135°附近测量偏差就明显改善,角度变化对形状变化不明显的条件下,特征更强的算法体现出了其高识别精度的优势.

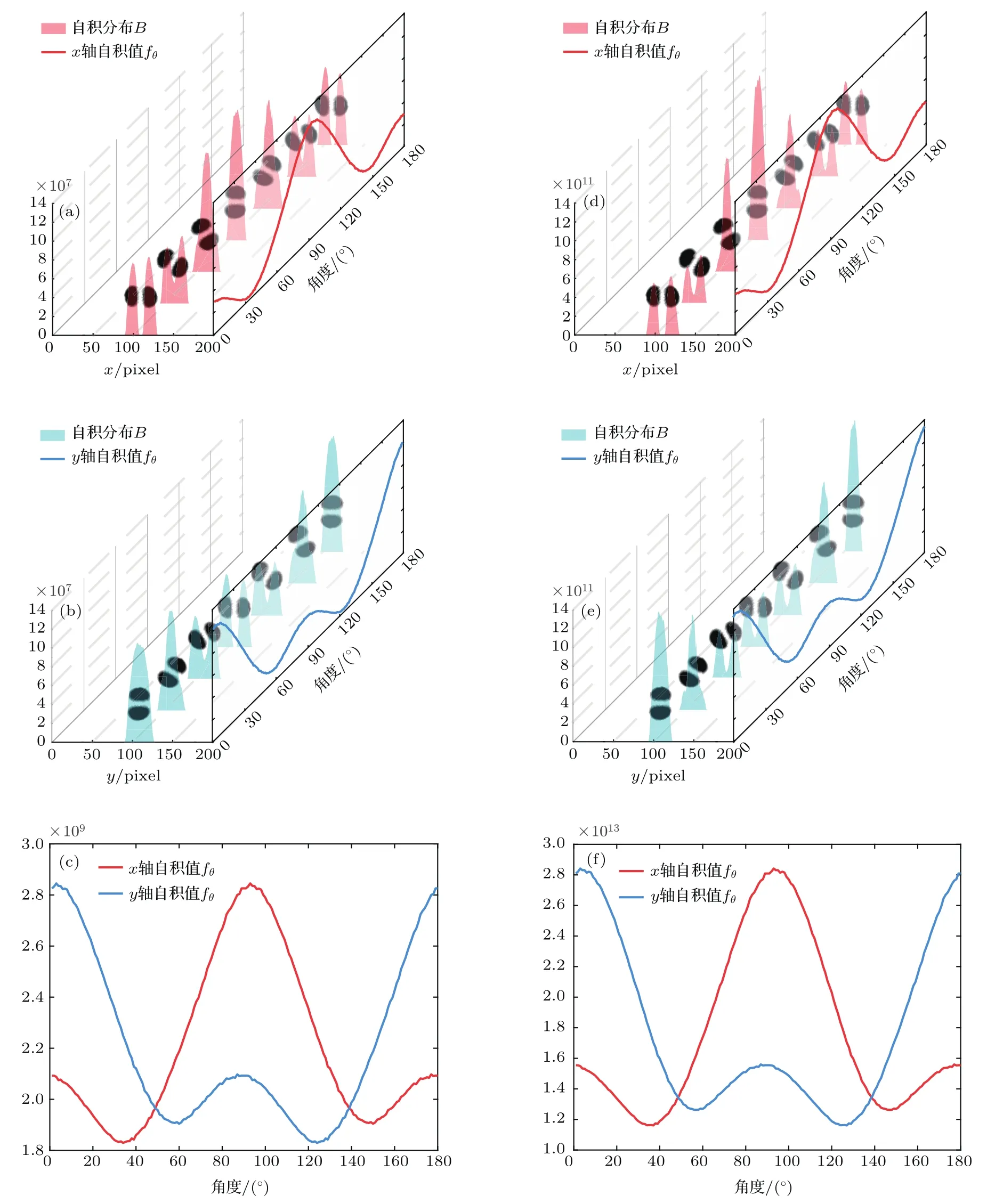
图6 LP11模式随角度旋转的二阶与三阶自积分布与自积值 (a)沿x轴的二阶自积分布与自积值;(b)沿y轴的二阶自积分布与自积值;(c)沿x轴与y轴的二阶自积值;(d)沿x轴的三阶自积分布与自积值;(e)沿y轴的三阶自积分布与自积值;(f)沿x轴与y轴的三阶自积值Fig.6.Second and third order self-integration and the distribution of self-integration in LP11mode with different angles:(a)Second order self-integration and the distribution of self-integration along x-axis;(b)second order self-integration and the distribution of self-integration along y-axis;(c)second order self-integration along x-axis and y-axis;(d)third order self-integration and the distribution of self-integration along x-axis;(e)third order self-integration and the distribution of self-integration along y-axis;(f)third order self-integration along x-axis and y-axis.

实验中声致光栅到双模光纤传感头之间的这段传输用双模光纤在未被固定并产生弯曲时,输出非对称模场分布会变化并影响最终测量精度,我们认为这是弯曲抖动所致的偏振态变化影响了模场的稳定性.最后为了研究轴向应力对旋转传感的影响,用移动平台在双模光纤传感头旋转的同时附加应力. 如图8所示,以从0°旋转到30°,60°和90°为例,在移动平台施加平行于光传输方向上100—1500µε之间,以三阶自积增强算法处理,最终测量误差小于0.08,也就是说小于阶自积增强算法本身的测量误差0.11.这一方面的发现使得基于模斑分布识别的光纤传感器能屏蔽轴向应变对旋转测量的影响.

图7 旋转角度的测量误差 (a)采用二阶自积法计算的测量误差;(b)采用三阶自积法计算的测量误差Fig.7.Measurement error of rotation angle:(a)Measurement error based on second order self-integration;(b)measurement error based on third order self-integration.

图8 应变对旋转角度的测量误差影响Fig.8.Effect of strain on measurement error of rotation angle.

4 结论

介绍了一种制备简单、结构紧凑的光纤声光旋转传感器.被加载上特定频率微波的压电陶瓷与少模光纤形成光纤声致光栅,使输入的激光模式转化为LP11模.将LP11模输出至自制双模光纤当作旋转传感头,传感光空间传输至CCD并经模场自积增强算法处理,计算出旋转方向和角度,记录动态旋转轨迹.这种基于模场解析的光纤传感器舍弃了传统光纤传感器中的频谱测量系统,减小了系统复杂性、降低了系统成本、增加了检测速度和时域动态检测功能.本文理论分析并实验了光纤声致光栅不同滤波深度对LP11模生成分布的影响.提出了专注于优化模场分析的自积增强算法,并实验了基于一阶、二阶和三阶自积增强算法的计算特性.实验中光纤声光旋转传感器在0°—180°广域范围内的检测值与标准值误差小于11%,分辨比例达到145%;并且在传输路径上100—1500µε环境下应力不敏感.基于模场检测传感采用图像处理的优势,希望在下一步的工作中能搭建在可见光波段工作的模场检测传感器,进一步优化自积增强算法,希望能让同一个传感头监测多种环境参量.

[1]Venanzi I,Cluni F,Gusella V,Materazzi A L 2007Proceedings of the 12th International Conference on Wind Engineering AWESCairns,Australia,July 2007

[2]Materazzi A L,Ubertini F 2011J.Sound Vibrat.330 6420

[3]Spanos P D,Chevallier A M,Politis N P,Payne M L 2003Shock Vib.35 85

[4]Rajnauth J,Jagai T 2012Int.J.Appl.Sci.Technol.2 109

[5]Zhu T,Rao Y J,Mo Q J 2006Acta Phys.Sin.55 249(in Chinese)[朱涛,饶云江,莫秋菊2006物理学报55 249]

[6]Huang B,Shu X 2016Opt.Express24 17670

[7]Song B,Miao Y,Lin W,Zhang H,Wu J,Liu B 2013Opt.Express21 26806

[8]Chen L,Zhang W G,Wang L,Zhang H,Sieg J,Zhou Q,Zhang L Y,Wang B,Yan T Y 2014Opt.Express22 31654

[9]Chen W,Lou S,Wang L,Zou H,Lu W,Jian S 2011IEEE Photon.Technol.Lett.23 1639

[10]Silva R M,Ferreira M S,Frazao O 2012Opt.Commun.285 1167

[11]Lou S Q,Lu W L,Wang X 2013Acta Phys.Sin.62 786(in Chinese)[娄淑琴,鹿文亮,王鑫2013物理学报62 786]

[12]Budinski V,Donlagic D 2016Opt.Express24 26282