角速度匹配法测量船体形变模型优化方法研究

王昱槐, 吴涛涛, 何佳洲

(江苏自动化研究所, 江苏 连云港 222061)

随着现代科学技术的进步和作战需求的提升,一大批大型水面作战舰艇如航空母舰、大型驱护舰、两栖攻击舰等陆续提上建造日程并投入服役,舰载武器也朝着高精度、高技术含量、高自动化方向发展。一般来说,此类大型作战舰艇上都配备了大量武器装备和观瞄设备,而这些舰载装备又根据作战任务不同分布于舰船不同战位点,为了保证这些设备的协调运行,舰船需向这些设备提供高精度的位置、速度和姿态信息,以保证建立起全舰统一的空间基准。然而,船体本身并非一个绝对刚体,这种非刚体特性使舰船在不同海况下产生三轴方向的形变角,形变角的产生会使得局部战位点相对于舰船摇摆中心产生基准误差,该误差已经成为制约舰载武器装备观瞄和打击精度的主要原因之一。为此,研究人员提出采用建立分立式捷联基准的方法,即在每个需要高精度基准信息的局部战位点处安装一套捷联基准,但该方法面临安装战位点多、型号庞杂、维护成本高、基准难以统一等问题,并不利于大型舰艇指控系统的发展。因此,如何精确测量船体形变角,以实现中心惯导高精度姿态信息向各局部战位点的精确传递和集中统一,对于提升舰载武器装备观瞄精度、建立全舰统一空间基准具有重要的现实意义。

自20世纪70年代以来,研究人员针对大型舰船形变测量问题提出了一系列方法[1],如偏振光能量测试法、大钢管基准法、双光源双CCD测量法、自准直平行光法、摄影测量法、应变仪测量法等结构力学方法,还有多部位安装航姿系统、GPS测量法、惯性测量匹配法等实时检测和修正的方法。其中,俄罗斯圣彼得堡电工学院A.V Mochalov等人于20世纪80年代末提出基于激光陀螺输出组件(LGU)的惯性测量匹配法[2],该方法由于其测量精度高、实时性好、抗干扰能力强等优点成为当前舰船形变测量中最具有发展潜力的研究方向。在此基础上,学者柳爱利提出了基于“速度+角速度”匹配的舰船甲板形变估计方法[3],该方法达到了10s内1″的估计精度;文献[4]针对激光陀螺形变测量系统提出了一种基于姿态匹配的船体形变测量方法,该方法避免了系统初始对准误差对形变测量的影响;文献[5]和文献[6]分别利用粒子滤波和容积卡尔曼滤波(CKF)解决了大角度形变条件下的船体形变测量问题;文献[7]和文献[8]在角速度匹配法的基础上,研究了激光陀螺零偏误差对形变估计的影响并提出了补偿方法;文献[9]研究了角速度匹配法测量船体形变中时间延迟对形变测量的影响机理和补偿方法,并通过实船实验数据验证了有效性。

上述有关惯性测量匹配法测量船体形变的文献中均将船体形变角分为静态形变角和动态形变角两部分予以分别建模,其中,将舰船静态形变角直接默认为一个不随时间变化的常值,动态形变角采用白噪声激励的二阶Markov过程模拟,模型中有关参数也人为设定为固定值。然而事实上,船体的静态形变角并非一个固定不变的常量,而是一直处于缓慢变化过程中,只是变化速度比较慢,周期相对较长,直接将其默认为不随时间变动的常值并不符合实际情况。

鉴于以上原因,本文在传统的角速度匹配法测量船体形变模型基础上,采用白噪声驱动的一阶Markov过程模拟由于外界温度变化、舰船载荷变化、转舵操作等原因造成的船体静态形变角缓慢变化过程,再将改进的“准静态”形变模型纳入滤波方程进行形变估计,最后通过仿真对改进前后的形变估计模型进行了验证和对比分析。仿真结果显示,当船体处于缓慢形变过程时,传统将静态形变角默认为常值的形变估计模型并不能估计出“准静态”形变过程,而改进的形变估计模型不仅可以稳定跟踪“准静态”形变过程,并且保持了较高估计精度,具有更好的适用性和有效性。

1 角速度匹配法测量船体形变模型

1.1 角速度匹配法测量船体形变原理

角速度匹配法测量船体形变原理如图1所示,假设在舰船摇摆中心Oxyz处和需要高精度姿态信息的战位点O′x′y′z′处分别安装一套惯性测量组件(IMU),如果船体是绝对刚体没有发生形变,则两套IMU输出的角速度信息是相同的;但如果船体发生形变,即坐标系O′x′y′z′相对于坐标系Oxyz发生了形变,记为φ=φ+θ,其中,φ表示静态形变角,θ表示动态形变角,则两套IMU会输出不同的角速度信息,因此可以将两套IMU输出的角速度之差作为观测量,建立角速度之差与动、静态形变角的线性关系,利用卡尔曼滤波方法实现对船体形变角的实时估计。

1.2 卡尔曼滤波方程的建立

(1)量测方程的建立

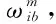
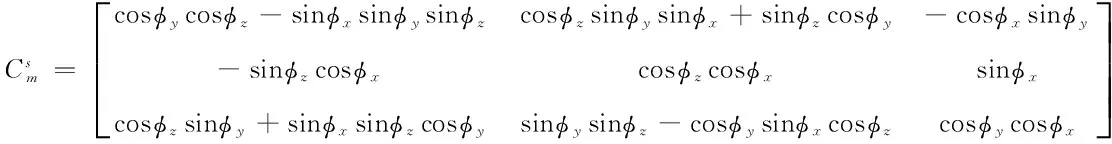
(1)

当三轴形变角均为小角度时,上式可近似为:

(2)

其中,[φ×]为φ=[φxφyφz]T的反对称矩阵。

同时,由于船体形变角的存在,两套IMU输出的角速度之间的关系如下:

(3)

进一步可以求得

(4)

考虑子惯导陀螺常值漂移和随机漂移的影响,上式可整理为

(5)

由上式可以看出,两套IMU输出的角速度之差和船体动、静态形变角之间存在线性转换关系,依据此关系,综合所选取的状态向量,可将上式写为卡尔曼滤波量测方程的标准形式:

Z=HX+V

(6)

其中,量测矩阵可表示为

2)系统方程的建立

根据船体形变角产生的原因,可以将船体形变角分为静态形变角和动态形变角两部分。其中,静态形变角主要由于船体受热不均和长时间的结构老化所造成,其特点是周期长、变化慢,在一定时间内可以认为是一个固定不变的常量,因此,静态形变角可表示为

φi=c(i=x,y,z)

(7)

进一步,静态形变角速度可以表示为

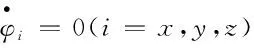
(8)

舰船在海上受到不同海况的影响,其动态形变和随机噪声驱动的随机过程相似,该过程可以用一个白噪声驱动的二阶马尔科夫过程来近似描述。动态形变角自相关函数可表示为

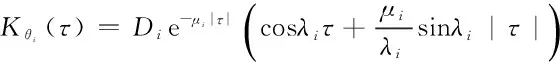
(9)

与其对应的形变滤波器方程可以表示为

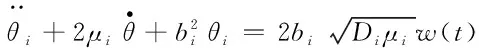
(10)

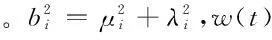
由于船体形变角的范围一般介于几角分到几十角分,而陀螺漂移的存在会给形变角测量精度带来严重的误差,因此有必要对陀螺漂移进行建模。

大量的统计规律表明,陀螺漂移主要由常值漂移和随机漂移两部分构成,其中,常值漂移可认为在一段时间内不随时间发生变化,近似理解为一个常数,即

ε0i=c(i=x,y,z)

(11)

而随机漂移εr=[εrxεryεrz]T也是一个随机过程,该随机过程的自相关函数可表示为

(12)

与其对应的形变滤波方程可以表示为

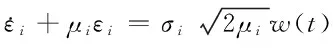
(13)

式中,i=x,y,z,μi表示不规则系数,τ表示相关时间,σi表示陀螺漂移离散程度的均方差。

综合式(7)、(10)、(11)、(13),将其写成卡尔曼滤波方程的标准形式:

(14)

其中,各矩阵分别为

A2=diag(-2μx,-2μy,-2μz)

A3=diag(-μεx,-μεy,-μεz)。

噪声输入矩阵B为:

综上所述,式(6)、(14)共同构成了角速度匹配法测量船体形变角的卡尔曼滤波模型。

2 引入“准静态”的静态形变角模型优化

引起舰船静态形变角的因素有很多:1)舰船在长时间风吹日晒和材料老化作用下,结构形状逐渐改变,产生长期变形;2)舰船在航行过程中载物分布的变化如燃料消耗、舰载机起降等导致甲板受力不均而产生的缓慢角形变量;3)舰船在机动过程中转舵操作也会引起船体短时间内的大幅形变,这种形变会在一定时间内恢复,但也有可能逐渐积累成为不可逆形变。

前文角速度匹配法中直接将船体静态形变角默认为一个绝对不变的常值,事实上,相关文献[10-13]表明,在太阳作用下舰船在一天之内会产生周期性的缓慢形变过程,美国于1972年在海军Stein号(DE-1065)上进行了24小时的静态形变测量,结果显示,一天之内-4°到24°温度变化情况下舰船在横摇方向上的形变大小约为0.05°。国内某型舰艇在六级海情下的形变测量实验也表明[14],舰船离惯导系统安装位置沿横轴方向±7m和沿纵轴方向±1.5m处绕纵摇轴形变为0.05°-0.08°,绕横摇轴的形变为0.17°-0.2°,在前后炮安装处的形变为0.23°,并且舰船在转弯时在航向方向引起了大约7″的角度变形,这种短时形变的变化周期(持续100s-200s)远大于舰船摇摆周期,也远远大于船体动态形变周期,不符合动态形变的二阶Markov模型,这种短时形变既不属于恒定不变的静态形变,也不属于动态形变,应该近似属于“准静态”形变范畴。

记“准静态”形变角速度为ωφ=[ωφxωφyωφz]T,由于随着时间的推移,“准静态”形变角速度可能发生缓慢变化,因此可以将“准静态”形变角速度看做白噪声驱动的一阶Markov过程,即

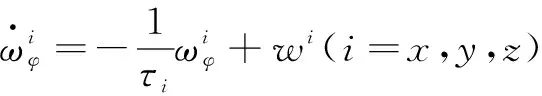
(15)

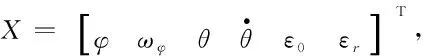
(16)

其中,各矩阵分别为:

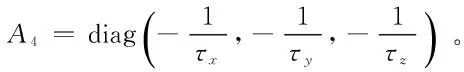
3 仿真与结果分析

3.1 仿真模型建立

由式(6)、(14)所示形变测量系统量测方程和系统方程,建立卡尔曼滤波器并进行仿真,仿真原理如图2所示。

其中,舰船运动模型用于产生舰船在三个轴向的运动信息,以激励两个IMU产生角速度输出,这里选取比较典型的三轴正弦运动来进行模拟,使用舰船(准)静态形变模型和动态形变模型模拟船体在三个轴向的变形过程,子惯导陀螺误差模型用于生成子惯导陀螺常值漂移和随机漂移误差,最后将形变信息和陀螺漂移信息叠加到子惯导陀螺输出上以生成子惯导相对于惯性坐标系的绝对角速度,最后经由卡尔曼滤波估计得到舰船三轴形变信息,并和真实动、静态形变值进行比较以得到估计精度。

3.2 仿真条件设置

1)假定两个IMU在测量之前已进行过初始对准和安装误差校准;

2)舰船以正弦规律绕航向轴、纵摇轴和横摇轴做匀速直线运动下的三轴摇摆运动,其模型为

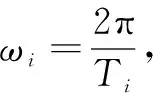
3)舰船静态形变角分别设为0.8°、0.3°、0.6°。考虑到“准静态”形变缓慢变化的特点,在纵摇和横摇方向上采用长周期正弦变化来模拟此类缓慢形变过程,由于舰船转舵操作可能引起船体产生短时大幅形变,因此在航向方向用长周期正弦变化的基础上叠加短周期正弦变化来模拟此类短时形变过程,其中,长周期正弦变化幅度为0.1°,周期为30min,短周期正弦变化幅度为0.2°,周期为4min,动态形变角满足二阶马尔科夫随机过程。

4)子惯导陀螺常值漂移为0.01°/h,随机漂移为0.001°/h。

3.3 仿真结果分析

图3、4、5、6为角速度匹配测量船体形变仿真结果,可以看出,在静态形变角设定为常值时,该方法可以在较短的时间内估计出静态形变角的大小,估计精度可以达到航向方向和纵摇方向5″、横摇方向15″,并具有较好的收敛性。对于动态形变角,该方法同样具有很好的跟踪效果,估计精度可达10″。

图7、8对比分析了当静态形变角为“准静态”形变过程时,优化的卡尔曼滤波模型对船体形变量的估计效果。可以看出,传统的将静态形变角默认为常值的滤波模型并不能估计并跟踪船体“准静态形变”过程,最后会产生巨大的估计误差,而优化的滤波模型不仅能准确跟踪静态形变角的缓慢变化过程,甚至在20min处出现短时间内较大幅度的形变时,该方法仍可跟踪这种短时形变过程,形变估计精度可以达到15″,显示了这种优化方法的正确性和实用性。

4 结束语

基于惯性测量单元的惯性测量匹配法是当前船体形变测量的发展趋势。本文系统推导了角速度匹配法测量船体形变的滤波模型,在该方法的基础上,从实际情况出发,引入“准静态”模型,给出了“准静态”模型下的角速度匹配形变测量方法,并进行了仿真验证。仿真结果显示,优化的形变估计模型在保持较高形变估计精度的基础上,更加符合实际形变过程,具有更好的实用性。未来,要推动惯性测量匹配法走向实际工程应用,更加符合真实情况的船体形变过程建模和长航时测量过程中陀螺漂移对形变估计影响的补偿,是需要进一步研究的主要课题。

[1] 朱昀炤,汪顺亭,缪玲娟,等. 船体变形测量技术综述[J]. 船舶工程,2007(6):58-61.

[2] Mochalov A A V, Kazantsev A V. Use of ring laser units for measurement of moving object deformations[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2002, 4680:85-92.

[3] 柳爱利,戴洪德. 基于惯性传感器输出匹配的舰船变形估计方法[J]. 传感技术学报,2011,24(1):145-148.

[4] 郑佳兴,秦石乔,王省书,等. 基于姿态匹配的船体形变测量方法[J]. 中国惯性技术学报,2010,18(2):175-180.

[5] 朱昀炤,汪顺亭,缪玲娟,等. 粒子滤波在船体大角度变形测量中的应用[J]. 北京理工大学学报,2008(4):343-346，351.

[6] 徐博,王艺菲,单为. 基于CKF的非线性船体变形惯性测量方法[J/OL]. 哈尔滨工程大学学报,2017,38(2):247-252.

[7] 杨云涛,王省书,黄宗升,等. 船体变形测量中激光陀螺零偏误差的补偿[J]. 仪器仪表学报,2014,35(12):2755-2761.

[8] 吴伟,秦石乔,杨云涛,等. 船体变形测量中激光陀螺误差的抑制机理[J]. 中国惯性技术学报,2014,22(5):665-670.

[9] 徐博,陈春,史宏洋,等. 基于FGU的船体变形测量技术中时间延迟补偿方法研究[J]. 船舶力学,2015,19(10):1235-1244.

[10] Titterton D, Weston J. Strapdown Inertial Navigation Technology[J]. Aerospace & Electronic Systems Magazine IEEE, 2004, 20(7):33-34.

[11] Titterton D, Weston J. Dynamic Shipboard Alignment Techniques[A]. Proceedings of DGON Symposium on Gyro Technology[C]∥Stutgart,Germany,1987.

[12] 汪顺亭,汪湛清,朱昀炤,等. 船体变形的监测方法及其对航向姿态信息的修正[J]. 中国惯性技术学报,2007(6):635-641.

[13] 姜广文. 像机链位姿传递摄像测量方法及船体变形测量研究[D]. 长沙:国防科技大学博士学位论文,2010.

[14] 万德钧,刘玉锋. 消减舰船变形的影响和为全舰提供高精度姿态基准[J]. 中国惯性技术学报,2005(4):77-82.