基于几何校正和LT码的鲁棒图像水印

章无用，陈建华

(云南大学 信息学院，云南 昆明 650500)

0 引 言

鲁棒水印算法大致可以分为以下3类：①基于不变域。将水印信息嵌入到对几何攻击具有不变性的域。如基于图像的不变矩[1-3]，将水印嵌入到矩的不变系数上，基于不变矩的算法对简单的几何攻击有一定的鲁棒性，而对不等比例缩放、剪切、组合几何攻击等鲁棒性较差。或者基于图像的某种变换[4-6]，一般情况下，此类算法鲁棒性较强，但是运算比较复杂，且水印嵌入容量较小。②基于图像特征[7-10]。从图像中提取出特征点，然后利用特征点构造某种不受几何形变影响的局部区域，将水印嵌入到这些与载体内容有关的特征区域，水印的检测也通过这些局部区域实现，此类算法抗攻击种类较多，缺点是嵌入容量有限。③基于模板校正的算法。利用模板估计几何形变的参数，然后实施逆变换，重同步并提取水印。Zhang等用Tchebichef矩估计几何攻击的参数并进行还原[11]，参数的估计较为精确，但实验结果表明只能抵抗一些常见的RST攻击；Lou提出一种基于特征点模板的算法来估计RST攻击的参数[12]，模板性能较为稳定，对一些简单的RST攻击性能较好；Wang等设计了具有几何不变性的可变形多尺度变换[13]，并基于此变换推导了几何同步机制，算法复杂度较低，但不能抵抗一般仿射变换等攻击，且水印提取时要用到原始图像；Wang等利用模糊支持矢量机(FSVM)估计几何失真的参数并进行校正[14]，算法嵌入容量大，对于单一的RST攻击效果较好，但抵抗组合几何攻击性能较差，并且不能抵抗一般仿射变换攻击。

综上所述，第①类算法不能有效地抵抗剪切、组合几何攻击等，第②类算法嵌入容量较小，第③类算法只能抵抗简单的几何攻击，对于剪切、RST的组合攻击、一般仿射变换攻击等鲁棒性较差。考虑到水印的嵌入容量、嵌入水印后载体图像的视觉效果以及对不同载体的普遍适用性，利用模板进行几何校正的方法具有相对较好的性能。同时，鉴于常见的基于模板校正的水印算法抵抗一般仿射变换、组合几何攻击性能较差的缺点，本文采用估计仿射变换矩阵并实施逆变换的方法解决此问题，更进一步，恢复几何形变的图像行列往往有细微的偏差，本文算法在空间域嵌入一层水印对变换域的版权保护水印的边界进行准确的定位。

本文方案先利用SIFT算法[15]从载体图像中提取并从中挑选出少量不易受几何形变影响的特征点作为模板，与受攻击的图像提取出的特征点进行匹配，再用RANSAC算法[2]进行挑选，剔除误匹配的特征点对，然后利用最小二乘法估计出仿射矩阵，对图像进行仿射逆变换，得到校正的图像。在经过仿射矩阵校正之后，图像的尺度还有轻微的偏差，图像的边界也遭到了破坏，故而本文算法将版权水印W1嵌在DWT-DCT的混合域，以承受像素的细微偏差，同时还利用奇偶量化法[7]在空间域嵌入定位水印W2，在校正各种几何形变后，精确定位DWT-DCT域版权水印W1的嵌入起点。最后，从几何校正图像的DWT-DCT域中提取出W1。针对大部分水印算法抗剪切攻击脆弱的状况，利用LT码[16]优异的纠删性能，将版权水印信息W1先经过LT码编码，再用失真补偿量化索引调制(DCQIM)算法[17]将编码水印信息嵌入到DWT-DCT混合域中，以达到抗剪切的目的。

1 SIFT特征点的提取和挑选

1.1 SIFT特征点提取

常见的图像尺度不变特征提取算法主要有Harris-Laplace[18]、SIFT、SURF[19]算法等，相对于Harris-Laplace、SURF算法，Lowe提出的SIFT算法具有更好的旋转和尺度不变性[20,21]，本文采用SIFT算法进行特征点的提取。其提取特征点的过程主要分为以下几个部分：①在DoG尺度空间检测极值，并且确定特征点的尺度和位置；②以Hessian矩阵H作为判断标准剔除边缘点和对比度低的点；③给每个特征点分配一个主方向；④SIFT特征向量的生成。

将原始图像与不同尺度的高斯核卷积便得到一组被平滑图像的尺度空间，尺度空间中相邻的图像相减便得到DoG多尺度空间，如图1所示，将DoG尺度空间中的每个点跟当前尺度空间周围的8个点以及相邻的上下尺度空间中对应位置的周围邻域9个点进行比较，仅当被检测的点的DoG值大于此26个点或小于此26点时，才将该点判定为极值点并保留以进行后续计算。

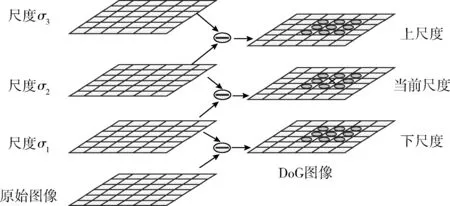
图1 DoG尺度空间局部极值检测

在求出极值点所处的位置和尺度后，利用2×2的Hessian矩阵H去除不稳定的特征点。

对每个特征点，在以其为中心的邻域窗口内利用直方图统计邻域像素的梯度分布，找到直方图的最高峰值便可确定特征点的主方向。

最后以特征点为中心、以特征点主方向为基准生成一个128维的特征向量。

1.2 特征点的挑选

从图像提取出几百甚至上千个特征点之后，首先去除大尺度和小尺度的特征点，因为尺度太大和太小的点在受到几何攻击后容易丢失。因此，对从载体图像中检测到的特征点，只保留中间尺度范围的特征点[7,22]。

接着，根据其对应的|DoG|值[7,15]大小，选出其中|DoG|值最大的特征点，设其坐标为(t1,t2)，对应的尺度为σ，生成圆形特征区域如式(1)

(x-t1)2+(y-t2)2=(kσ)2

(1)

然后从剩下的特征点中选出|DoG|值最大，且由式(1)确定的特征区域与之前的区域不重叠的特征点，重复上述操作，根据图像纹理丰富程度的不同选出20个左右的特征点。同时将这些特征点的特征向量作为密钥进行保存，用于水印检测时仿射矩阵的估计。特征点的选择过程如图2所示，以图像Lena为例。

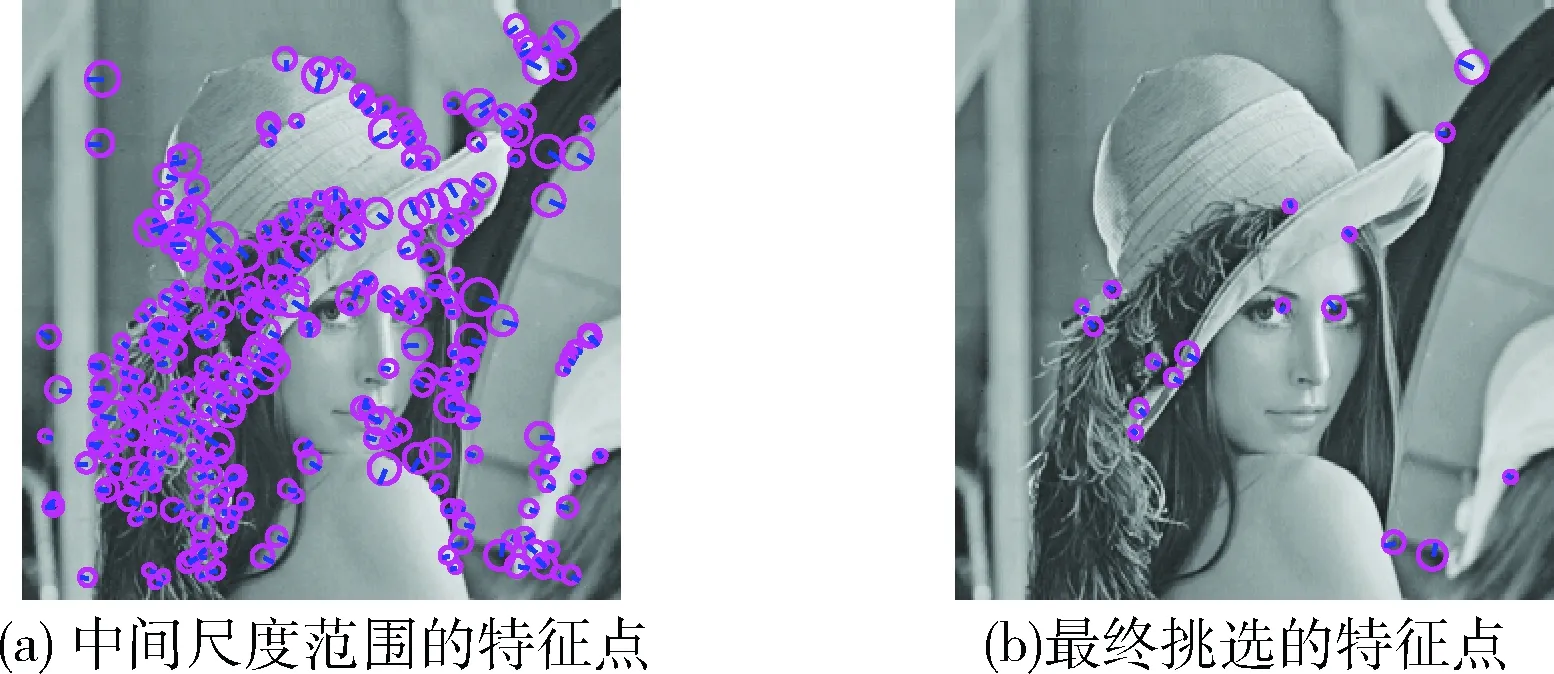
图2 特征点的挑选

2 几何攻击检测与校正

通常情况下，图像仿射变换前后的坐标关系如式(2)

(2)

点(u,v)为原始坐标、(x,y)为仿射变换后的坐标，其中仿射矩阵A为

(3)

由于平移系数Tx、Ty不能影响到仿射矩阵A，故而完全可以在求出仿射矩阵A并对受攻击的图像进行几何校正之后，根据校正后图像的相应特征点与密钥中特征点之间的对应关系求出Tx、Ty，因此关键是根据匹配特征点间的关系求出A。虽然仿射矩阵A随攻击顺序不同而变化，如式(4)为先旋转、再缩放、后沿X轴方向错切、最后沿Y轴方向错切的过程，但本文采用匹配特征点的关系求A，避免了多数基于模板校正的算法需要判断攻击顺序，估计旋转、缩放参数等繁琐的过程

(4)

在水印的检测端，利用SIFT算法从受攻击的载体图像中提取特征点及相应的特征向量，与密钥中的原始特征点进行匹配，假设Ωi(i=1,2,…,n1)为从受攻击图像提取的特征点，Uj(j=1,2,…,n2)为原始的特征点，则Ωi、Uj的相似度可以用它们相应向量之间的欧氏距离表示，距离越小则特征点的相似度越高，但这样很可能出现误匹配，为减小因误匹配而导致的仿射矩阵估计的误差，本文采用RANSAC算法[2]对特征点进行挑选，以提高特征点的正确匹配率。RANSAC算法实际操作过程如下：

输入:少量的原始特征点U,受攻击图像提取的特征点Ω,最大的循环次数Cmax,允许的最大误差εmax。输出:N2组匹配误差较小的特征点对。for i=1 to Cmax do 从U,Ω随机选择3组匹配的特征点对求得仿射矩阵A1,并令N1=0; for allP∈U do //P为原始特征点 if|Ω(P')-U(P)A1|<εmax then //P'为与P相匹配的特征点 N1=N1+1 endif endfor if N1>N2 //N2的初始值为3 N2←N1 endif endfor

经过RANSAC算法的挑选，基本剔除了误匹配的点，然而，实际上剩下的匹配的特征点可能本身就存在误差，本文使用最小二乘法来最小化误差。构建目标函数为

(5)

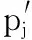
3 水印嵌入与提取过程

3.1 版权水印W1的实现

针对现有的一些水印算法，比如常见的基于不变域、模板校正的水印算法抗剪切性能较差的现象，本文先将水印信息W1进行LT码编码，编码后得到比特流W1(b)，b=1,2,3…。

LT码具有良好的纠删性能，但并不能检错，故而需加入校验码，将出错的LT码编码数据包检测出来并删除。本文使用检错功能较强的CRC码进行检错，在LT编码数据包后面加入一定长度的CRC码。

由于几何攻击和校正过程破坏了数字图像的边缘，增加或减少了一些行和列，为了降低水印W1的误码率，W1不嵌到整幅图像，而是嵌在离边缘还有一定距离的图像块中。因此，先对水印W1嵌入区域进行一级DWT变换，由于低频子带LL1集中了主要能量，将水印嵌入到该子带中将具有很好的鲁棒性。然后，对LL1进行8×8的DCT变换，再利用DCQIM算法将水印嵌入到DCT变换块的中低频系数中，具体操作流程如下：

(1)在需要嵌入W1编码比特流的DCT变换块i中选取8个备选嵌入点，其位置记为j，j=1,2,3,…,8,并将嵌入点的DCT系数[23]记为fi(j)。

(2)在8个备选嵌入点中选择c(1≤c≤8)个点，作为嵌入的位置。

(3)按照式(6)进行W1编码比特流的嵌入

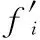
(6)

式中：γ为量化补偿参数，取值在0～0.25之间[17]，aj为量化步长，表示JPEG标准量化表中与位置为j的嵌入点对应的量化系数，Qm是量化器，其定义如下

(7)

(4)编码水印信息嵌入后，再进行IDCT、IDWT得到嵌入编码水印W1的载体图像。

版权保护水印W1的提取过程如下：

(1)利用空域W2的水印信息搜索几何校正的图像，定位W1嵌入起点，过程详见3.2节，同时截取水印W1嵌入部分。

(2)将嵌入水印W1的部分图像进行一层DWT,对LL1进行8×8的DCT变换，然后到相应的DCT变换块系数中，按式(8)提取水印比特流W1(b)′

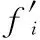
(8)

其中

(9)

3.2 空间域水印W2的实现

水印W2是利用奇偶量化法嵌入在空间域的3个特定位置，如图3所示。一个大方块由若干个小方块组成，一个小方块由若干像素构成，每个小方块嵌入1 bit信息。并且每个小方块嵌入的水印信息与它周围的小方块是相异的，以增强定位的精准性。

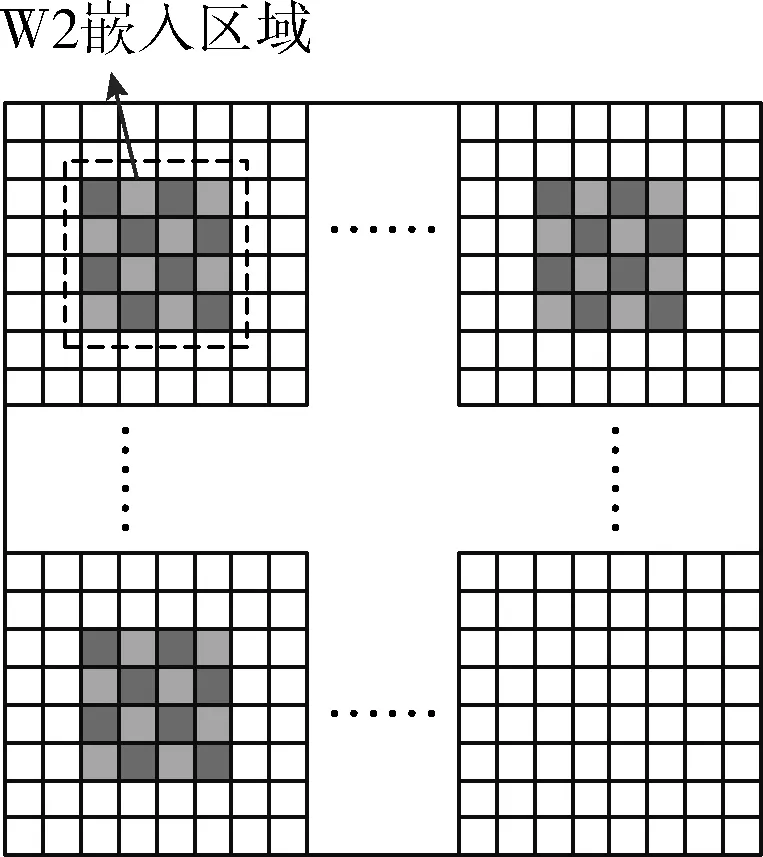
图3 W2嵌入区域

具体的嵌入过程如下：

(1)对所要嵌入区域的每个像素I(x,y)计算量化函数值Q(x,y)，其中Δ表示量化步长

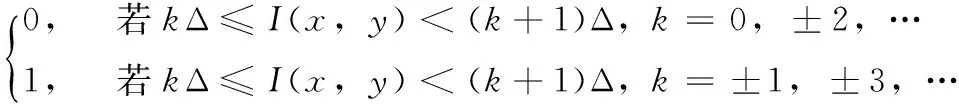
(10)

(2)求出每个像素的量化噪声δ(x,y)

(11)

(3)确定像素的修改量m(x,y)，使修改后的像素值处于量化区间的中点

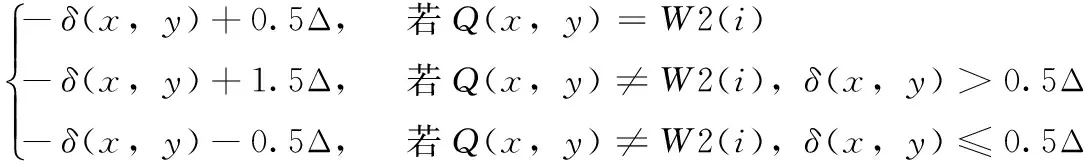
(12)

(4)修改后的像素值为I*(x,y)=I(x,y)+m(x,y)， 对区域内的每个像素进行上述操作，得到嵌入水印W2的载体图像。

W2的提取方法如下：对几何校正后的图像进行与嵌入过程相同的方块分割，然后对每个小方块内的像素利用式(10)计算量化函数值，并记第i个方块内函数值为0的像素个数为CNTi,0，函数值为1的像素个数为CNTi,1，通过式(13)提取水印W2′

(13)

(14)

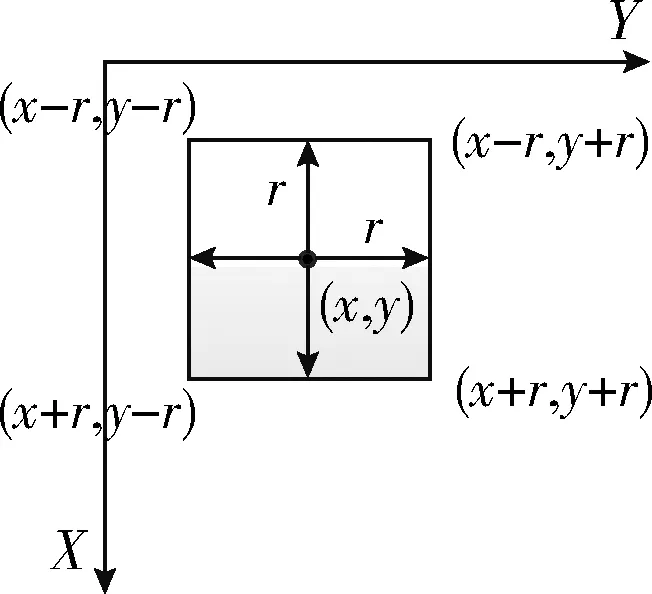
图4 搜索区域

4 实验结果与分析

4.1 相关说明

实验使用的仿真工具为2011b版MATLAB。以嵌入容量、透明性、鲁棒性为评价指标。并与文献[6]、文献[8]中的算法进行了对比。采用256级512×512的标准灰度图像Lena、Peppers、Airplane作为测试图像，如图5所示，水印W1是480 bits的二值伪随机序列，LT编码数据包的长度为1，CRC编码时，信息位与校验位长度都是6 bits，每个8×8的DWT-DCT块嵌入6 bits，嵌在前6个低中频系数上，则一幅载体图像嵌入5400 bits，编码冗余度为4.625；编码水印W1的嵌入区域的起点为(17,17)，宽度和高度都是480，量化步长aj分别为JPEG量化表[23]对应系数的2.5倍。

图5 原始测试图像

水印的透明性可用原始图像与嵌入水印的载体图像之间的峰值信噪比PSNR[5]来表示。W2为48 bits，分别嵌入到图像空域的3个特定位置，这3个特定位置应尽量选有一定纹理、边缘等视觉不易感知的区域，奇偶量化步长Δ需考虑到视觉隐蔽性、鲁棒性，根据所嵌区域纹理的不同，Δ取10～14之间的值，其中3.2节中的β取0.85，并且这3个特征位置的距离须尽量远些，在本文中，W2的嵌入起点分别为(25,25)、(25,463)、(463,25)，每个大方块嵌入16 bits，一个大方块由16个小方块组成，每个小方块含36个像素。嵌入两层水印后，它们对应的PSNR分别为41.2963 dB、41.4121 dB、41.1659 dB。

水印的鲁棒性用原始水印与提取水印之间的相关系数NC[7]及提取水印的误码率BER[5]两个参数来描述。

4.2 抗常见几何攻击

常见的几何攻击主要包括旋转、缩放、剪切、错切、仿射变换等。表1列出了本文算法抗此类攻击的性能，并与文献[6]的算法进行了对比。

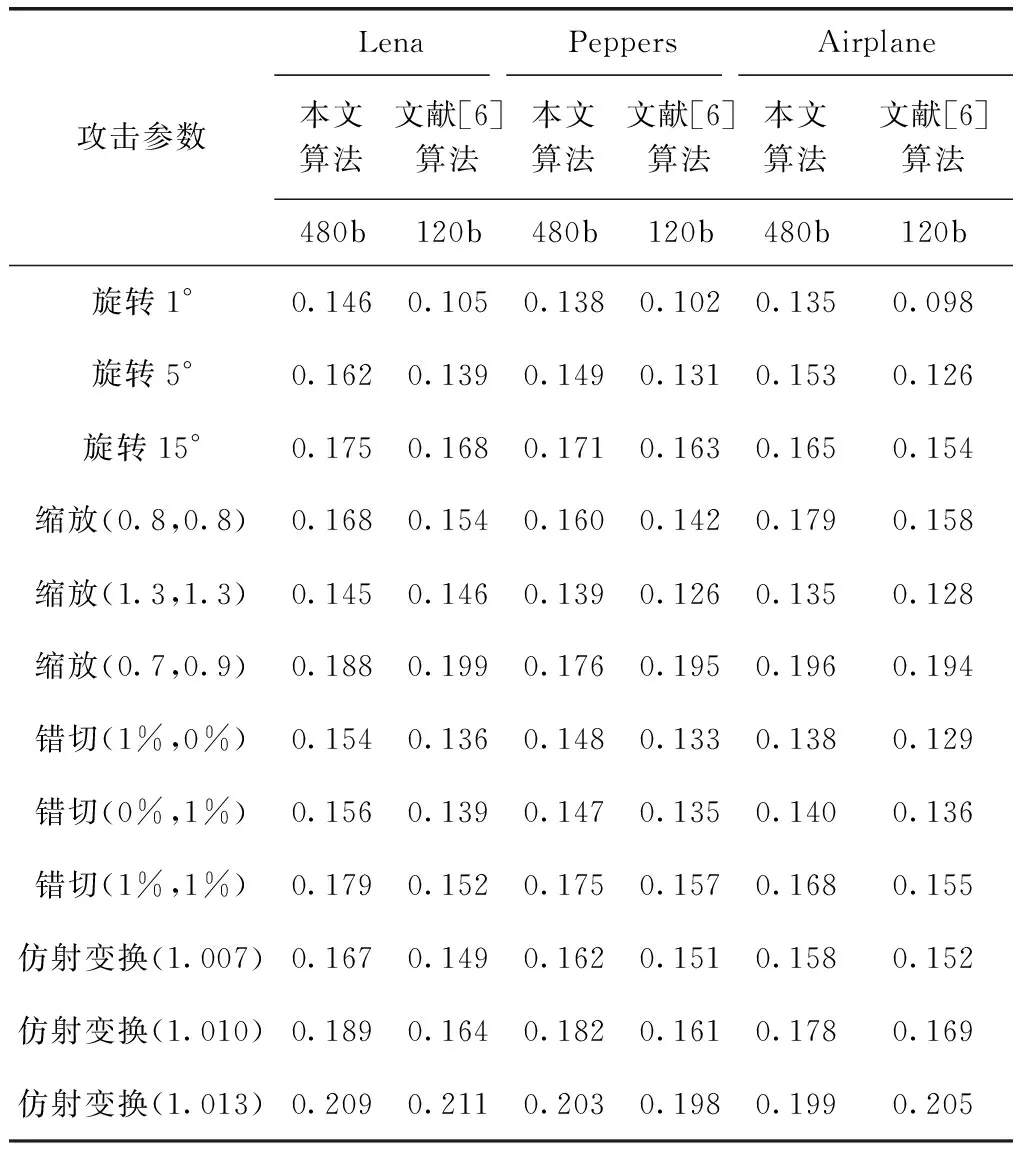
表1 常见几何攻击下的BER

对于剪切攻击，本文算法性能优异，表2为剪切攻击下本文算法的NC。剪切攻击后的图像如图6所示(以Lena为例)，被剪切部分补全黑。

在表1中，旋转攻击是不带剪切的，仿射变换(1.007；1.010；1.013)对应的仿射矩阵分别是[1.007 0.01；0.01 1.012]；[1.010 0.013；0.009 1.011]；[1.013 0.008；0.011 1.008]；从表1可知，对于常见的几何攻击，本文算法与文献[6]的BER相近，但本文的嵌入容量是其3倍，故而本文保持BER较低的情况下，嵌入容量有较大的提升。

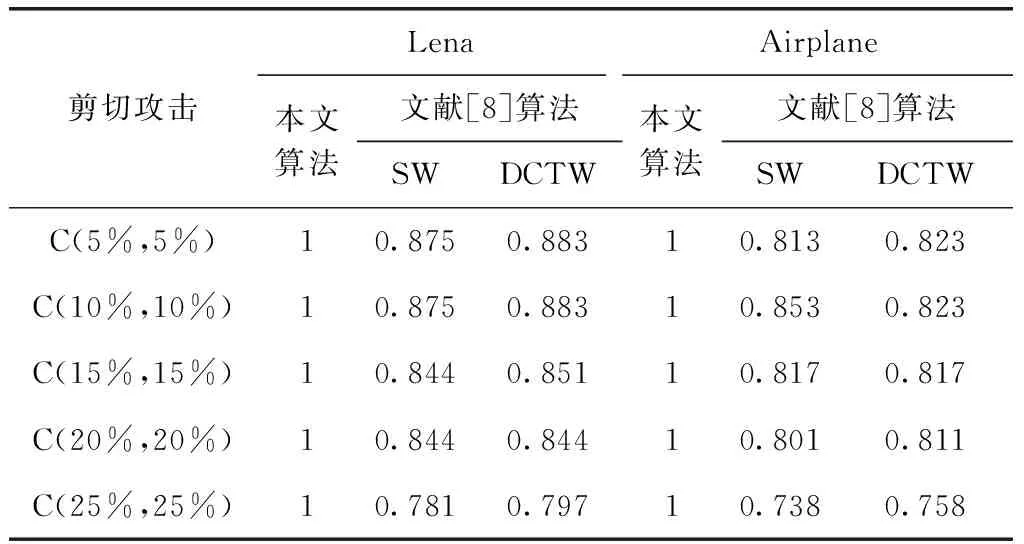
表2 不同尺度剪切攻击下的NC

图6 不同尺度剪切攻击后的图像(Lena)

至于剪切攻击，本文算法在较低剪切尺寸下，能够完整的恢复水印，与文献[8]的空间域(SW)、DCT域(DCTW)的实验结果对比见表2。文献[8]的嵌入容量是128 bits，鲁棒性的评价指标是提取水印与原始水印之间的NC，表2中列出的是本文算法在剪切攻击下NC的变化情况。只有在剪切尺度超过50%，LT码的冗余度过小导致解码不成功才会使NC急剧下降。

4.3 抗组合几何攻击

图像在传播过程中会遭受到多种多样的攻击，组合几何攻击就是比较常见的一种，表3列出了本文算法在部分组合几何攻击下BER的变化情况。

综合以上的实验结果可以推知，对于常见的几何攻击，即便是组合几何攻击，本文算法具有较好的性能，而且有较大的嵌入容量。因为本文算法对几何攻击的仿射矩阵进行了比较精确的估计。本文算法对于随机删除行列、随机扭曲等攻击稍差，因为本文算法是基于图像的全局几何校正。

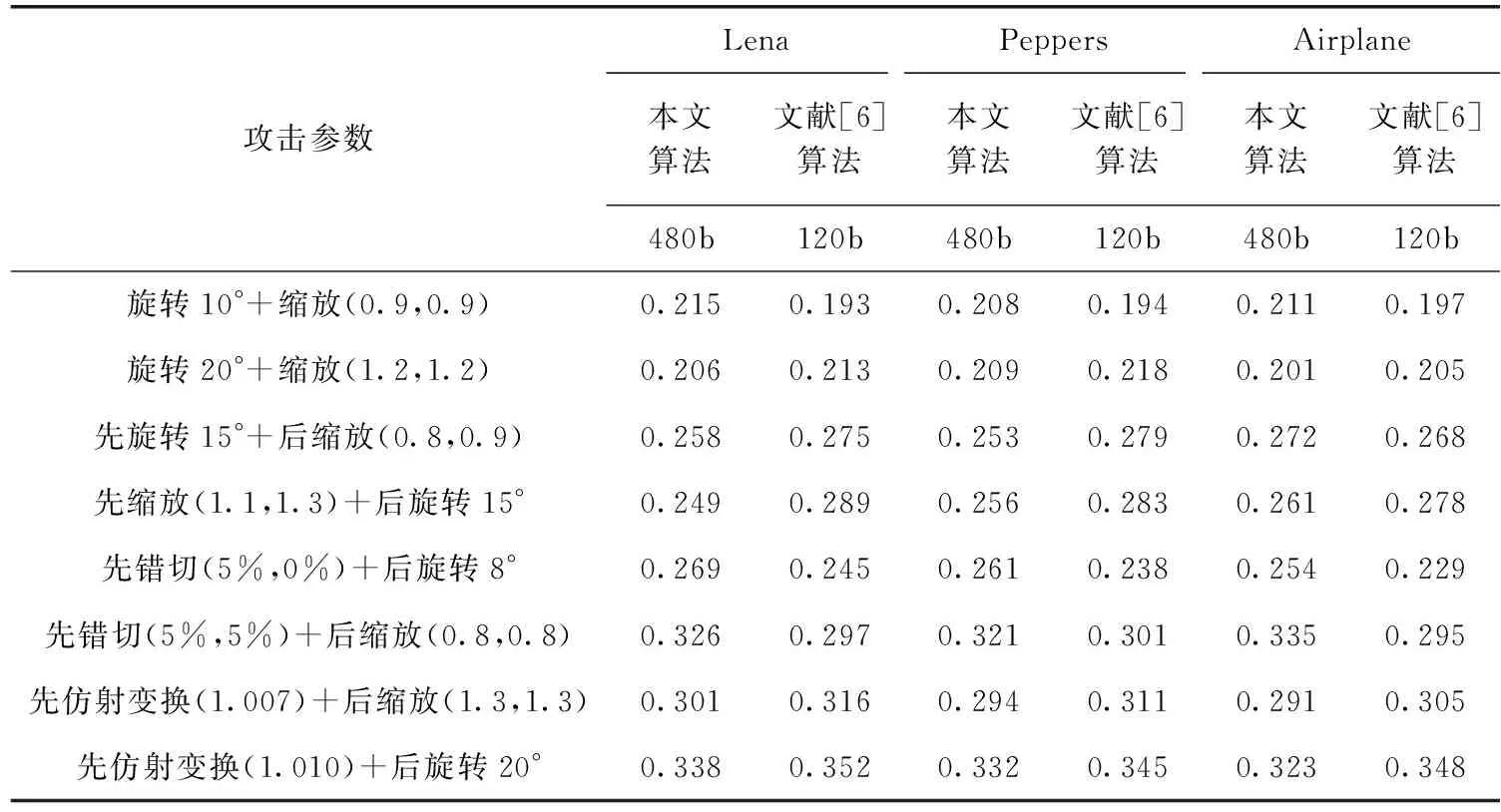
表3 组合几何攻击下的BER

5 结束语

如何有效抵抗不同种类的几何攻击，同时保持较高的嵌入容量，一直是困扰水印研究者的一个难题。本文使用对仿射矩阵进行精确估计，并且在空间域嵌入一层水印对变换块的边界进行准确的定位的方法来解决此问题。首先利用SIFT算法提取攻击前后图像特征点，采用RANSAC算法对匹配的特征点对进行挑选，使用最小二乘法拟合出仿射矩阵，使仿射矩阵的估计误差最小化，然后对受攻击的图像进行仿射逆变换以校正图像的几何形变，最后利用空间域水印精准定位出变换域版权水印的嵌入起点。实验结果表明：本文算法不仅对于常见的几何攻击有较强的鲁棒性，同时，相较于一般的水印算法，本文算法抗组合几何攻击性能较好且嵌入容量较大；更进一步，针对大部分鲁棒水印算法抗剪切性能差的缺点，将水印信息经过LT码编码后嵌入到载体图像中，充分发挥LT码抗删除的优点，因此本文算法还具有良好的抗剪切性能。

[1]Xin Y,Liao S,Pawlak M.Circularly orthogonal moments for geometrically robust image watermarking[J].Pattern Recognition,2007,40(12):3740-3752.

[2]Ryu SJ,Kirchner MJ,Lee MJ,et al.Rotation invariant localization of duplicated image regions based on Zernike moments[J].IEEE Transactions on Information Forensics & Security,2013,8(8):1355-1370.

[3]Wang Chunpeng,Wang Xingyuan,Xia Zhiqiu.Geometrically invariant image watermarking based on fast radial harmonic Fourier moments[J].Signal Processing:Image Communication,2016,45(C):10-23.

[4]Simitopoulos D,Koutsonanos DE,Strintzis MG.Robust image watermarking based on generalized radon transformations[J].IEEE Transactions on Circuits & Systems for Video Technology,2003,13(8):732-745.

[5]Li LD,Li SS,Abraham A,et al.Geometrically invariant image watermarking using polar harmonic transforms[J].Information Sciences,2012,199(16):1-19.

[6]He Xuansen,Zhu Tao,Yang Gaobo.A geometrical attack resistant image watermarking algorithm based on histogram modification[J].Multidimensional Systems & Signal Processing,2015,26(1):291-306.

[7]LI Leida,GUO Baolong,BIAO Jinfeng.Spatial domain image watermarking scheme robust to geometric attacks based on Odd-Even quantization[J].Journal of Electronics & Information Technology,2009,31(1):134-138(in Chinese).[李雷达,郭宝龙,表金峰.基于奇偶量化的空域抗几何攻击图像水印算法[J].电子与信息学报,2009,31(1):134-138.]

[8]Lin YT,Huang CY,Lee GC.Rotation,scaling,and translation resilient watermarking for images[J].Image Processing Iet,2011,5(4):328-340.

[9]FANG Xiaozhao,ZHANG Wei,TENG Shaohua,et al.Di-gital watermarking scheme based on SVM of SIFT features[J].Computer Engineering & Design,2011,32(11):3609-3612(in Chinese).[房小兆,张巍,滕少华,等.基于SIFT特征区域的支持向量机数字水印方法[J].计算机工程与设计,2011,32(11):3609-3612.]

[10]Su PC,Chang YC,Wu CY.Geometrically resilient digital image watermarking by using interest point extraction and extended pilot signals[J].IEEE Transactions on Information Forensics & Security,2013,8(12):1897-1908.

[11]Zhang Li,Qian Gongbin,Xiao Weiwei.Geometric distortions invariant blind second generation watermarking technique based on Tchebichef moment of original image[J].Journal of Software,2007,18(18):2283-2294.

[12]LOU Oujun,WANG Zhengxuan.A Contourlet-domain watermarking algorithm against geometric attacks based on feature template[J].Chinese Journal of Computers,2009,32(2):308-317(in Chinese).[楼偶俊,王钲旋.基于特征点模板的Contourlet域抗几何攻击水印算法研究[J].计算机学报,2009,32(2):308-317.]

[13]WANG Chuntao,NI Jiangqun,ZHUO Huashuo,et al.A geometrically invariant robust image watermarking based on deformable multi-scale transform[J].Acta Automatica Sinica,2011,37(11):1368-1380(in Chinese).[王春桃,倪江群,卓华硕,等.基于可变形多尺度变换的几何不变鲁棒图像水印算法[J].自动化学报,2011,37(11):1368-1380.]

[14]Wang Xiangyang,Liu Yunnan,Li Shuo,et al.Robust image watermarking approach using polar harmonic transforms based geometric correction[J].Neurocomputing,2016,174(22):627-642.

[15]Lowe DG.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(60):91-110.

[16]Mackay DJC.Fountain codes[J].IEE Proceedings Communications,2005,152(6):1062-1068.

[17]Korus P,Biaas J,Dziech A.A new approach to high-capacity annotation watermarking based on digital fountain codes[J].Multimedia Tools & Applications,2014,68(1):59-77.

[18]Mikolajczyk K,Schmid C.Scale & affine invariant interest point detectors[J].International Journal of Computer Vision,2004,60(1):63-86.

[19]Bay H,Ess A,Tuytelaars T,et al.Speeded-up robust features[J].Computer Vision & Image Understanding,2008,110(3):346-359.

[20]Luo J,Gwun O.A comparison of SIFT,PCA-SIFT and SURF[J].International Journal of Image Processing,2009,3(4):143-152.

[21]ZHAO Xiaochuan.Improve and applicable case detail of processing technology of modern digital image(MATLAB Version)[M].Beijing:Beihang University Press,2012:44-74(in Chinese).[赵小川.现代数字图像处理技术提高及应用案例详解(MATLAB版)[M].北京:北京航空航天大学出版社,2012:44-74.]

[22]DENG Cheng,GAO Xinbo.Geometrically robust image watermarking based on SIFT feature regions[J].Guangzi Xuebao,2009,38(4):1005-1010(in Chinese).[邓成,高新波.基于SIFT特征区域的抗几何攻击图像水印算法[J].光子学报,2009,38(4):1005-1010.]

[23]SU Na.Research and application of digital wartermarking algorithm based on DCT transform domain[D].Chengdu:University of Electronic Science and Technology of China,2016(in Chinese).[苏娜.基于DCT域的数字图像水印算法的研究与应用[D].成都:电子科技大学,2016.]