云环境下求解大规模优化问题的协同差分进化算法

谭旭杰，邓长寿，吴志健，彭虎，朱鹊桥

差分进化算法(differential evolution，DE)是一种基于实数编码的全局优化算法[1]，因其简单、高效以及具有全局并行性等特点，近年来已成功应用到工业设计和工程优化等领域。研究人员对DE算法进行了改进和创新并取得了一些成果。比如Brest等[2]构造了控制参数的自适应性方法并提出了自适应DE算法(jDE)。Wang等[3]提出了复合DE算法(CoDE)，其将精心选择的3种变异策略和3组控制参数按照随机的方法进行组合。这些研究成果主要集中于低维问题(30维)，然而当面向高维问题(1 000维)时，这些DE算法的性能将急剧下降，而且搜索时间随着维数成指数增长，求解极为困难，“维灾难”问题依然存在[4]。

为了有效求解高维优化问题，学者们提出不同的策略，其中具有代表性的是协同进化(cooperative coevolution，CC)[5]。CC 采用“分而治之”的思想，首先将高维复杂问题分解成低维简单的子问题；其次对每个子问题分别进行求解；最后通过所有子问题解的协同机制，得到整个问题的解。Yang等[6]提出的随机分组策略，可将两个相关变量以极大的概率放在同一组，在大规模优化问题中得到较精确的解。研究人员已将CC应用到多个领域，如大规模黑盒优化问题[7]、SCA 问题[8]、FII算法[9]、CCPSO 算法[10]、DG2 算法[11]，然而它们在求解高维优化问题时，采用串行方式求解，因此，问题求解需要较长的计算时间，很难在有效时间内提供满意的解。近年来云计算已应用到大规模信息处理领域中，如在机器学习[12]、蚁群算法[13]、CRFs算法[14]、差分进化算法[15-16]、图数据分析[17]、分类算法[18]等获得了成功。因此，有必要将云计算的分布式处理能力与CC的优势相结合，为大规模优化问题的求解提供新方法。

研究人员已在Google开源平台Hadoop的Map-Reduce模型之上提出了一些分布式差分进化算法[19-20]。实践中研究人员发现，MapReduce模型是一个通用的批处理计算模型，缺乏并行计算数据共享的有效机制，对迭代运算无法提供有效支持。因此，基于MapReduce模型的差分进化算法需要通过频繁读写文件来交换数据，降低了其效率[21]。

Spark云平台是伯克利大学提出的分布式数据处理框架[22]，在许多领域获得了成功应用。Spark提出了一种全新的数据抽象模型RDD(弹性分布式数据模型)。RDD模型能够有效支持迭代计算、关系查询、批处理以及流失数据处理等功能，使得Spark可以应用于多种大规模处理场景。由于RDD模型基于内存计算，避免了MapReduce模型频繁读写磁盘数据的弊端，提高了效率。

本文基于Spark云平台提出了合作协同的差分进化算法。SparkDECC算法采用“分治”策略，将高维优化问题按随机分组策略分解成低维子问题，并封装成RDD；在RDD中，每个子问题独立并行进化若干代；利用协同机制将所有子问题合并成完整问题，评价出最优个体。SparkDECC算法在13个标准函数进行测试，实验结果表明该算法是有效可行的。

1 差分进化算法

差分进化算法是一种仿生的群体进化算法，具体操作如下[23]。

1) 种群初始化

DE算法首先在[xmin，xmax]范围内随机初始化NP个D维向量xi的种群，其中NP为种群大小，D为种群的维度，xmin为最小值，xmax为最大值，i∈[1, NP]。

2) 变异

变异主要是通过种群中个体之间的差向量来改变个体的值。DE算法根据基准向量的选取和差分向量数目不同，有多种变异操作。本文的目标向量xi主要通过最常用的变异算子产生，如式(1)。

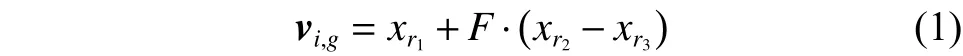
式中：i, r1, r2, r3∈[1, NP]且互不相同的4个随机整数；vi,g为目标向量xi在第g代时产生的变异向量；缩放因子F∈[0, 1]。

3) 交叉

变异后，DE算法通过交叉概率在目标向量xi与变异向量vi进行交叉，产生新的试验向量ui。具体操作如式(2)所示。

式中：交叉概率 CR∈[0, 1]，j∈[1, D]，随机数rnd1∈[0, 1]，随机整数 rnd2∈[1, D]。

4) 选择

DE算法主要通过“贪婪”原则对个体进行选择，较优个体进入下一代。具体操作如式(3)所示。

式中f (xi,g)为个体xi,g的适应度值。

DE算法通过变异、交叉、选择之后，根据循环代数或求解精度来结束搜索。

2 合作协同的云差分进化算法Spark-DECC

2.1 Spark云平台

为了更加高效地支持迭代运算，Spark平台在MapReduce云模型的基础上进行了扩展[24]。Spark平台提供了两个重要的抽象：RDD和共享变量。RDD本质是一个容错的、并行的数据结构，提供了一种只读、分区记录并存放在内存的数据集合。Broadcast是一种共享变量，将数据缓存在每个结点上，不再需要传递数据，减少通信开销，提高通信性能。Spark平台的API为RDD提供了两种算子：转换算子(Transformations)和动作算子(Actions)，其中，转换算子都是惰性的，对RDD分区的每个数据执行相同的操作，并返回新的RDD；而动作算子将触发RDD上的运算，并将值返回给主控结点。RDD内部实现机制基于迭代器，使得数据访问更高效，避免了中间结果对内存的消耗，使迭代计算更加高效快速。

DE是一种基于群体的进化算法，具有内在并行性的特点。因此，DE能与Spark的并行性充分融合。Spark在主控结点通过Parallelize方法将种群并行初始化，并采用“键–值”的方式存放在内存中，即：

式中：m是子种群的数目；keyi是整数，表示第i个子种群的编号；valuei是第i个子种群。DE在Spark上的具体实现如图1所示。

图1 基于Spark的DE算法Fig. 1 DE based on spark

Spark将内存中的数据按“键–值”对的方式抽象成RDD，并根据keyi值将子种群分区保存在不同的结点上。利用RDD的并行操作算子对各子种群并行进化若干代，再通过collect算子合并生成新的种群。循环结束后通过动作算子reduce获取整个种群的最优值。

2.2 SparkDECC算法

CC框架处理大规模优化问题优势明显。然而，随着种群规模的增加，CC框架所需时间快速增加。为了提高CC框架的收敛速度，将云计算的优势与CC框架相结合，提出了基于Spark的合作协同进化算法-SparkDECC算法。

SparkDECC算法首先将高维问题按随机分组方法分解成若干个低维子问题，一个子问题对应一个子种群，保留每个子问题在完整问题的位置信息；按keyi值将低维子种群分发到RDD中相应的分区，每个分区中的子种群并行执行DE算法的变异、交叉、选择等操作，其中子种群在计算个体适应度值时，选取上一轮的最优个体合作组成完整的种群并进行局部寻优。低维子种群在对应的分区中进化若干代后，按照其位置信息合并成新的完整种群，并通过全局搜索返回最优个体。SparkDECC算法的流程图如图2所示。

图2 SparkDECC算法流程图Fig. 2 Flowchart of SparkDECC algorithm

SparkDECC算法的具体步骤如下。

1) 初始化参数：种群规模NP、缩放因子F、交叉概率CR、问题的维度D、子问题的维度DimSub、子种群数M=D/DimSub、子种群的位置信息subscript、分区数Num、进化代数Gen、子种群合并轮数Cycles；

2) 初始化种群Pop，通过cache()将数据存放在内存中；

3) 获取种群最优个体向量bestInd、最优值best；

4) 将控制合并轮数的变量c赋值为0;

5) 判断合并轮数c是否小于等于Cycles，若是，则循环结束；否则，继续；

6) 变量c自动加1;

7) 利用parallelize方法将Pop按随机分组策略分解成M个低维的子种群，将子种群的位置信息存放subscript中，并按key值将子种群分发到相应分区；

8) 通过broadcast变量将Pop广播至每个结点；

9) 各子种群并行进化Gen代，具体的计算过程为：

① 变异操作，执行式(1)；

② 交叉操作，执行式(2)；

③ 选择操作，执行式(3)，其中子种群在计算适应度值时，按照其位置信息替换掉bestInd中的部分解。

10) 利用collect动作算子将所有低维子种群按协同机制合并成完整种群，并更新Pop；

11) 对Pop进行全局搜索并返回最优个体bestInd；

12) 转到 5)；

13) 循环结束，通过reduce返回最优值best。

在上述SparkDECC算法中，包含两个循环，即6)、10)。外循环6)控制问题的全局优化，内循环10)控制子问题的局部优化。

上述算法的时间复杂度主要集中在10)，其主要功能是在Num个分区中同步并行优化M个低维子问题。一个低维子问题的时间复杂度为O(M×NP)，M个低维子问题在一个分区里按串行方式进化Gen代，运行Cycles轮的时间复杂度为O(M×NP×Gen×Cycles)。在上述算法中，略去其他步的时间复杂度。因此，SparkDECC算法在每个分区的时间复杂度为O(M×NP×Gen×Cycles)/Num。

3 数值实验与分析

3.1 测试问题

为了测试SparkDECC算法求解大规模优化问题的性能，本文选取了文献[25]中13个测试函数进行实验。其中f1～f8为单模函数，f9～f13为多模函数，f4和f5为不可分解的函数，其他函数都是可分解的。函数的详细说明详见文献[25]。

3.2 实验设置

本实验采用Spark云模型，每个节点的配置如下：64 bit corei7 CPU，主频3.4 GB，内存8 GB，Ubuntu13.10操作系统，安装使用Hadoop2.2.0和Spark1.2.0，编程环境为IntellJ IDEA14.1.2，使用Scala和Java语言。

为了验证SparkDECC的性能以及影响其性能的各个因素，实验时SparkDECC中问题的维度D=1 000，子问题的维度DimSub=100，问题规模NP=100，F=0.5，CR=0.9，每个子种群独立运行的代数MaxGen=100，合并轮数Cycles=50。为了验证SparkDECC算法的可扩展性，将问题的维度D扩展到5 000，其他参数保持不变。

3.3 实验结果与分析

表1为 SparkDECC 与 OXDE[26]、CoDE、jDE、PSO[27]算法的平均最优值和标准方差的结果对比。5种算法的参数设置一致，各算法独立运行25次。采用了Wilcoxon秩和检验方法对4种算法的实验结果进行了统计分析，显著性水平为0.05，其中，“–”表示劣于，“+”表示优于，“≈”表示相当于。

表1中，SparkDECC与其他3种DE算法进行对比，结果表明，SparkDECC 在 f1、f5、f6、f10～f13共7个函数能快速收敛到最优结果，实验数据优于其他3种算法；SparkDECC算法在f3、f8和f9等3个函数的收敛出现了停滞，实验结果弱于其他算法；在不可分解函数f4上各算法的运行效果相当；f2要劣于jDE，优于OXDE和CoDE；带噪声函数f7的实验结果劣于CoDE，优于jDE，与OXDE相当。

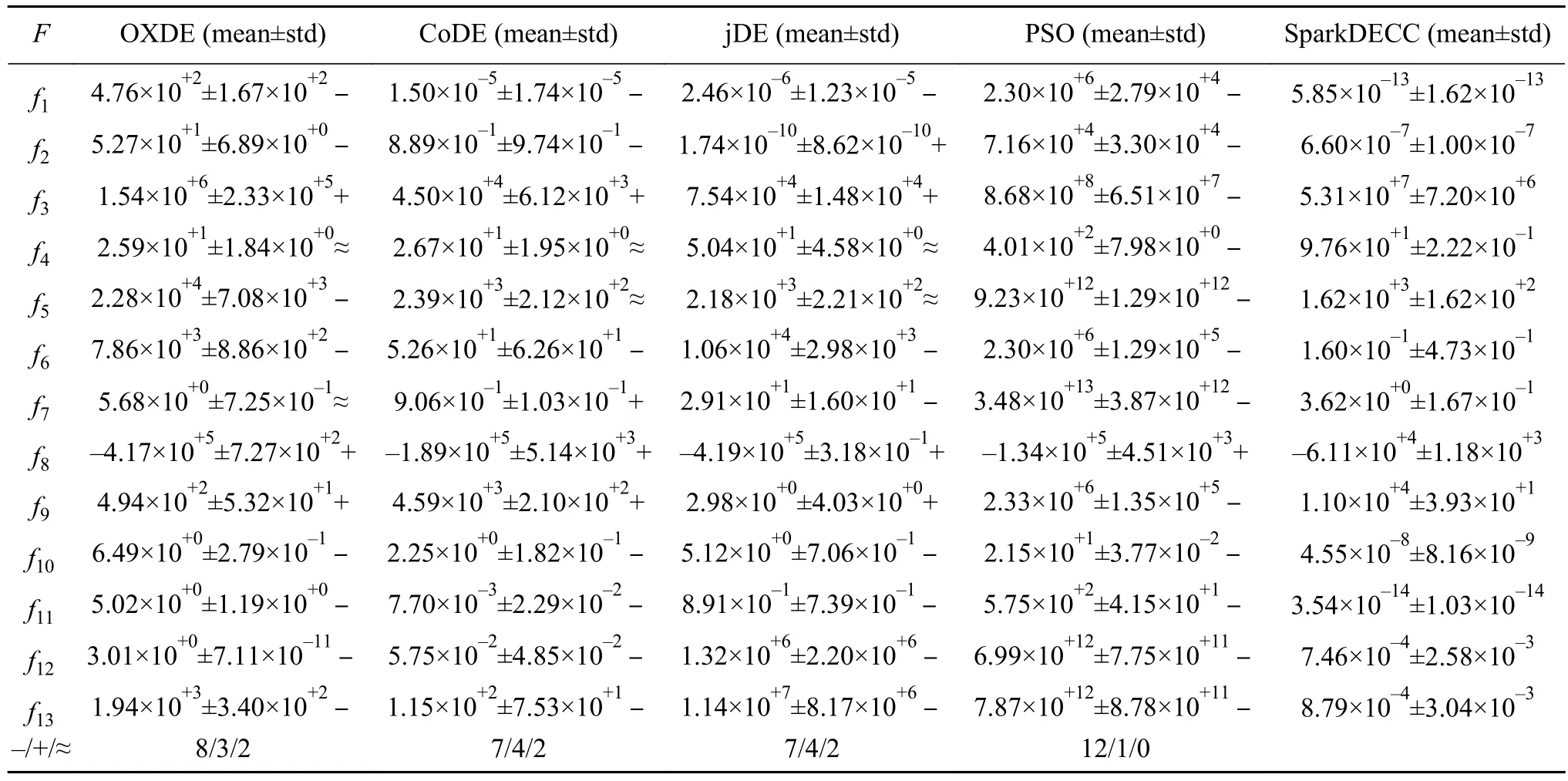
表1 SparkDECC、OXDE、CoDE、jDE、PSO算法的平均值、标准差和Wilcoxon秩的检验结果Table 1 Comparison of SparkDE, OXDE, CoDE, jDE and PSO algorithms for solving the results

SparkDECC与PSO算法的结果对比，实验结果表明SparkDECC算法除函数f8外其他都优于PSO，说明SparkDECC算法总体性能优于PSO。

函数收敛曲线图主要用来表示算法求解最优值的一种趋势走向，函数曲线下降得越快，收敛性能越好。为了比较 4 种不同 DE 算法在 f1、f3、f5、f6、f9、f10、f11、f13等函数的收敛性能(受篇幅限制，仅选择这8个函数)，选取了各算法独立运行20次中的平均收敛数据，收敛取值以10为底的对数形式，曲线图如图3所示。从图3可以看出SparkDECC算法的收敛能力较强，在函数f1、f10、f11上的收敛曲线呈直线下降，收敛性能强；函数f5、f6、f13在进化的前期有很好的收敛速度，但在后期出现了一定程度的局部收敛；函数f3，f9在整个进化过程中处于局部收敛，收敛性能弱，收敛效果要劣于其他算法。

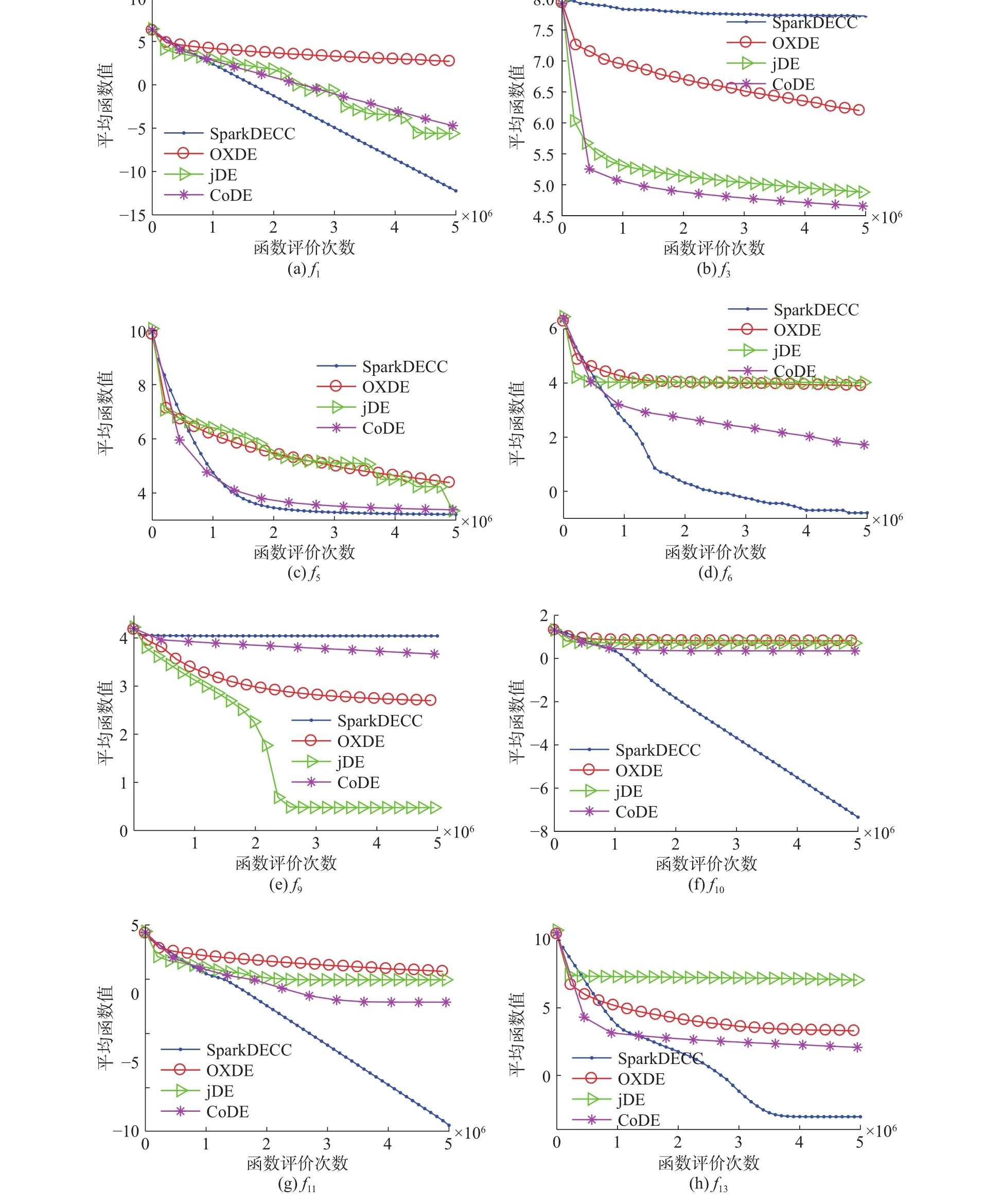
图3 收敛图Fig. 3 Convergence graph

综合以上实验数据分析表明，SparkDECC算法能有效地求解大规模优化问题，提高了DE算法的收敛精度和收敛速率。

加速比[28]是衡量算法并行性的有效指标，其定义如式(5)所示。

图4 加速比Fig. 4 Acceleration ratio

3.4 协同方式对算法性能的影响

SparkDECC算法对子种群进行局部寻优后，需要合并所有子种群并进行全局搜索。SparkDECC算法按照原模型进行组合，整个种群保持原来的结构。为了分析子种群合并机制对SparkDECC算法性能的影响，本文选取了两种不同的协同方式进行对比实验。这两种协同方式衍生出两种算法，即SparkDECC-1算法和SparkDECC-2算法，这两种算法在SparkDECC算法的基础上，子种群按不同的协同方式进行组合。其中，SparkDECC-1算法在所有子种群组合之前，首先将所有子种群的个体按其适应度值升序排序，最后将所有子种群按线性方式组合成完整的种群；SparkDECC-2算法将所有子种群中的个体按随机方式组合成完整的种群。为了验证3种不同的SparkDECC算法的性能，选择了相同的参数设置，分别在13个函数上独立运行20次，实验结果如表2所示。

表2的实验结果表明，SparkDECC算法在f1、f2、f4、f5、f10、f11、f12、f13等 8 个函数的实验结果要优于其他两种协同方式。其中，SparkDECC-1算法在f3、f6、f8、f9等 4 个函数优于 SparkDECC 算法，SparkDECC-2算法中的所有函数都劣于Spark-DECC算法。总之，SparkDECC算法的其他组合方式不能有效地提高算法的收敛精度，且增加了种群个体的排列组合运算，算法的运行时间随之增加。因此，SparkDECC算法选择最初的协同方式合并子种群，维持原种群的结构，能有效提高算法的精度和时间。

表2 SparkDECC 3种不同协同方式的实验结果Table 2 Experimental results of SparkDECC on three different cooperative modes

3.5 子种群数对算法的影响

为了分析子种群数对SparkDECC性能的影响，分别选取了不同数目的子种群进行对比实验，如1、2、5、10、20等5种不同的子种群。根据2.2节中的子种群数的计算公式，计算子种群的维度，如问题维度为1 000，则上述5种不同子种群的维度分别为 1 000、500、200、1 00、50。算法的其他参数设置保持一致，分别在13个测试函数上独立运行了20次，表3和表4分别记录了5种不同子种群数下的平均最优值和平均运行时间。

表3 和表 4 的结果分析发现，f1、f2、f6、f8、f10、f12、f13共7个函数的收敛精度随子种群数的增加而逐渐增强。f3、f4、f9这3个函数解的精度在种群不分解的情况下达到最优，种群维度的分解并没有提高解的精度。f7的解在子种群数为5时达到最优，再增加子种群数并不会提高解的精度。f5、f11的解在子种群数为10时达到最优。因此，对于可分解函数，SparkDECC的种群多样性随子种群数的增加逐渐增强，提高了解的收敛性。然后，随子问题数目增多，子问题之间的交互时间随之增加，从而增加了函数的收敛时间。表4的结果显示，函数的运行时间与子问题数成正比，与2.2节中的时间复杂度相吻合。当子问题数增加到20时，13个函数总的平均时间是1个子问题的11.5倍。因此，Spark-DECC应从收敛时间和收敛精度两方面综合考虑选取合适的子种群数。

3.6 子种群进化代数对算法的影响

SparkDECC算法在子种群进化若干代后，需要合并成新的全局最优解。因此，为了探索子种群局部寻优的代数Gen对SparkDECC算法的影响，本文选取了10、20、50、100、250等5种情况分别进行实验。5种情况的其他参数一致并设置相同的函数评价次数，分别独立运行25次，平均运行时间及结果分别如表5和表6所示。

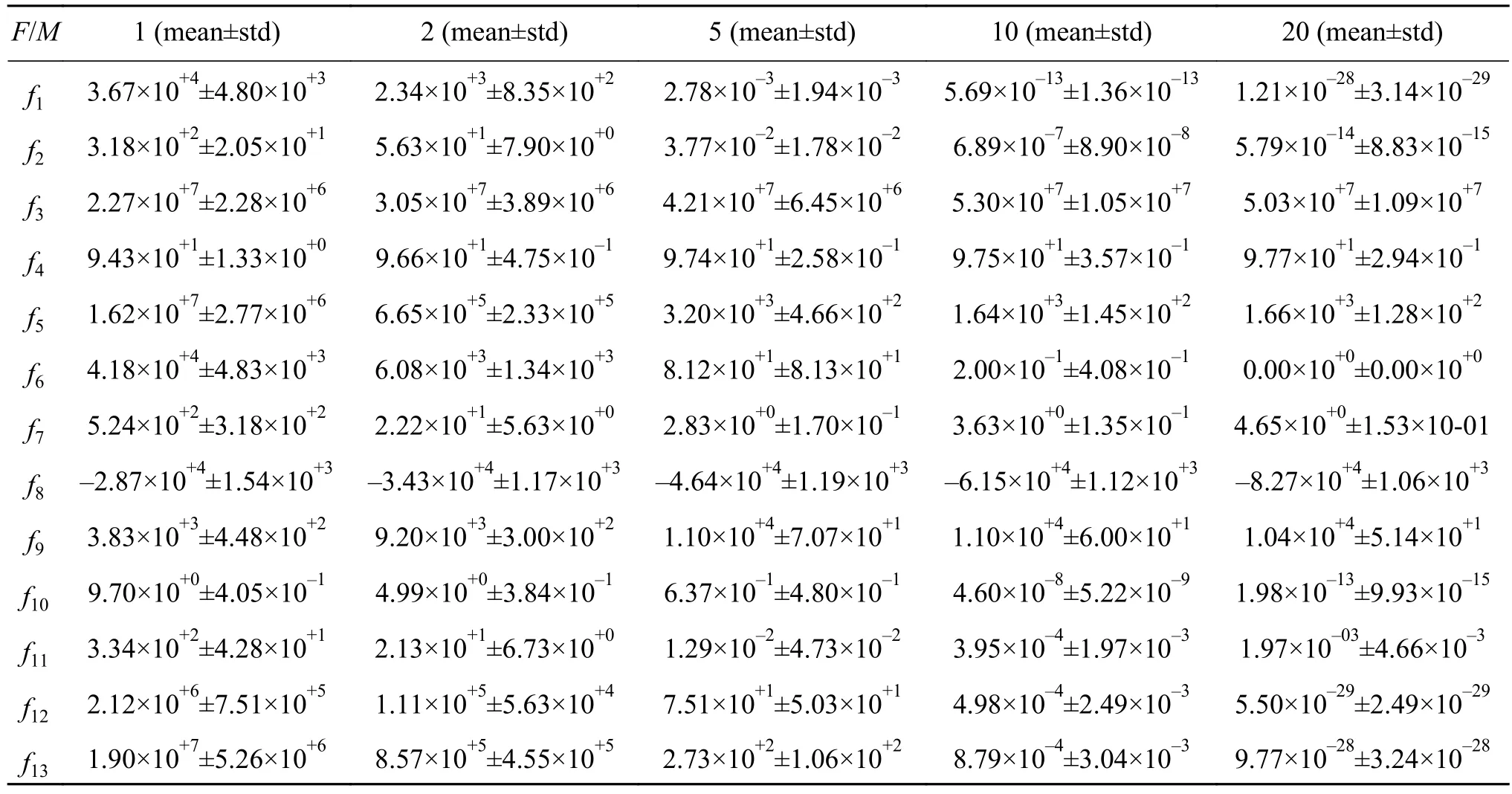
表3 SparkDECC在不同子种群数的实验结果Table 3 Experimental results of SparkDECC in different number of sub-populations

表4 SparkDECC在不同子种群数的平均运行时间Table 4 The average running time of SparkDECC in different number of sub-populations ms

表6 的结果显示，f1、f2、f7、f8、f9、f10等 6 个函数的求解精度随进化代数的增加逐渐提高。f3和f4两个函数增加局部寻优的代数并不能提高解的精度，函数易陷入局部最优。f6、f12和f13等3个函数的结果在进化代数为100时达到最优。f5和f11两个函数在进化代数为50时达到最优，进化代数的增加并不能提高解的质量。由2.2节中的时间复杂度可知，在评价次数相同的情况下，不同进化代数Gen的函数优化时间几乎相同。但从表5的结果显示，SparkDECC算法的优化时间随参数Gen的增加而逐渐减少。其主要原因是，由2.2节中的算法可知，SparkDECC算法在评价次数相同的情况下，合并轮数Cycle的值随进化代数Gen变大而逐渐变小，减少了广播变量执行的次数，因此，函数的优化时间会相应减少，但总的优化时间相差无异。

表5 进化代数对SparkDECC优化时间的影响Table 5 Optimization time of SparkDECC with generations ms

总之，SparkDECC算法的收敛精度与子问题的进化代数和合并轮数关系紧密，增加子问题的进化代数提高了子问题的局部寻优能力。子问题的合并轮数改善了问题多样性。但是，在评价次数相同的情况下，子问题的合并轮数随子种群进化代数的增加而减少。因此，为了在全局搜索和局部寻优之间达到平衡，并能在有效时间内提高算法的收敛精度，我们可以选择合适的进化代数，合理分配计算资源。

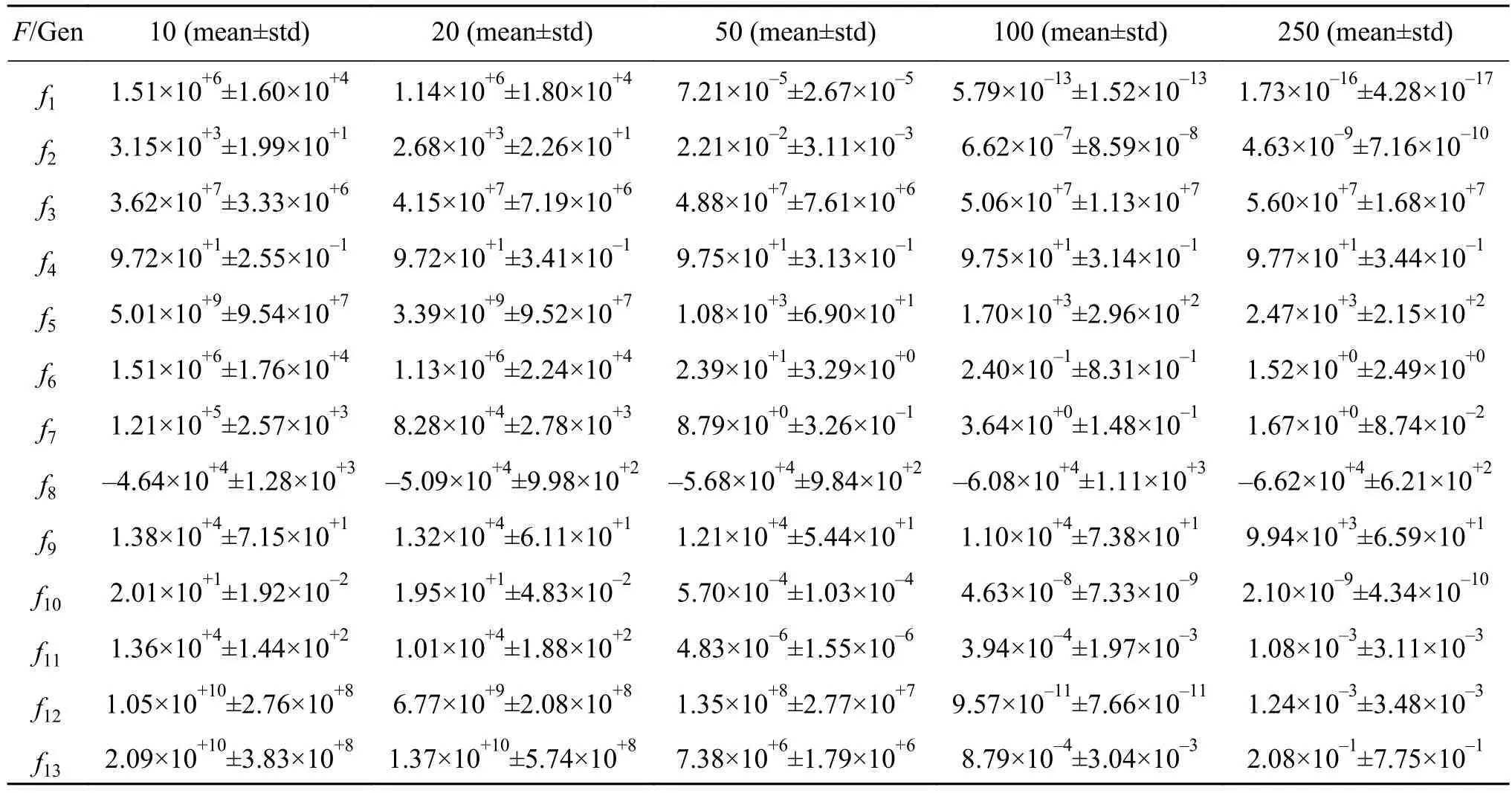
表6 进化代数对SparkDECC优化性能的影响Table 6 Performance affection of SparkDECC with generations

3.7 SparkDECC算法的可扩展性分析

为了验证SparkDECC算法的可扩展性，本文将文献[25]中的13个测试函数扩展到5 000维进行实验。子问题的维度 S=100，F=0.5，CR=0.9，FES=5 000 D，问题规模NP=100，算法独立运行10次。OXDE、CoDE和jDE 3种算法在5 000维的实验参数与SparkDECC的参数一致，实验结果如表7。

表7 SparkDECC、OXDE、CoDE、jDE算法在5 000维的平均值、标准差和Wilcoxon秩和检验结果Table 7 Comparison of SparkDECC, OXDE, CoDE, jDE algorithms for solving the results in 5 000 dimension

表7的结果显示，随着维度的增加，算法的求解性能下降，搜索时间成倍增长。SparkDECC算法在 f1、f2、f5、f6、f7、f8、f10、f11、f12、f13等 10 个函数的最优值都优于其他3种算法，但在f3和f9两个函数的最优值都劣于其他3个算法，4种算法在函数f10上的结果相似。OXDE、CoDE和jDE 3种算法在13个测试函数的维度扩展到5 000时的运行时间分别是25.15天、16.68天和16.85天。SparkDECC算法的运行时间为4.71天，大大提升了算法的收敛时间。实验结果显示，SparkDECC算法在5 000维的整体性能优于其他3种算法，具有很好的可扩展性。

4 结束语

本文利用新型的迭代云计算模型，提出新的基于Spark的合作协同云差分进化算法(SparkDECC)。SparkDECC算法按随机分组策略将高维问题分解成多个同维的低维子问题，将每个子问题与RDD模型中的分区一一对应，每个子问题并行执行DE算法，子问题独立进化若干代后，更新最优个体，提高种群的多样性。利用Scala语言在Spark云模型上实现了SparkDECC，通过13个标准测试函数的对比实验，结果表明SparkDECC求解精度高，速度快，可扩展性好。此外，选择6个测试函数进行加速比实验，实验结果表明加速比与分区数量几乎是线性的，加速效果良好。后续工作将在SparkDECC的基础上探索新的分组策略，并不断改进其协同机制，提高算法的收敛效率和求解精度。

[1]STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over conti-nuous spaces[J]. Journal of global optimization, 1997, 11(4):341–359.

[2]BREST J, GREINER S, BOSKOVIC B, et al. Self-adapting cont-rol parameters in differential evolution: a comparati-ve study on numerical benchmark problems[J]. IEEEtransactions on evolutionary computation, 2006, 10(6): 646–657.

[3]WANG Yong, ZHANG Qingfu. Differential evolution with composite trial vector generation strategies and co-ntrol parameters[J]. IEEE transactions on evolutionary computation, 2011, 2(15): 55–66.

[4]FRANS V D B, ENGELBRECHT A P. A cooperative approach to particle swarm optimization[J]. IEEE transactions on evolutionary computation, 2004, 8(3): 225–239.

[5]POTTER M A, De JONG K A. A cooperative coevolutionary approach to function optimization[J]. Lecture notes in computer science, 1994, 866: 249–257.

[6]YANG Z, TANG K, YAO X. Large scale evolutionary optimization using cooperative coevolution[J]. Information sciences, 2008, 178(15): 2985–2999.

[7]MEI Y, OMIDVAR M N, LI X, et al. A competitive divideand-conquer algorithm for unconstrained large-scale blackbox optimization[J]. ACM transactions on mathematical software, 2016, 42(2): 13.

[8]GUAN X, ZHANG X, WEI J, et al. A strategic conflict avoidance approach based on cooperative coevolution-ary with the dynamic grouping strategy[J]. International journal of systems science, 2016, 47(9): 1995–2008.

[9]HU X M, HE F L, CHEN W N, et al. Cooperation coevolution with fast interdependency identification for large scale optimization[J]. Information sciences, 2017, 381: 142–160.

[10]LI X, YAO X. Cooperatively coevolving particle swarms for large scale optimization[J]. IEEE transactions on evolutionary computation, 2012, 16(2): 210–224.

[11]OMIDVAR M N, YANG M, MEI Y, et al. DG2: a faster and more accurate differential grouping for large-scale black-box optimization[J]. IEEE transactions on evolutionary computation, 2017, 21(6): 929–942.

[12]MENG X, BRADLEY J, YUVAZ B, et al. Mllib: machine learning in apache spark[J]. Journal of machine research,2015, 17(34): 1235–1241.

[13]王诏远, 王宏杰, 邢焕来, 等. 基于Spark的蚁群优化算法[J]. 计算机应用, 2015, 35(10): 2777–2780.WANG Zhangyuan, WANG Hongjie, XING Huanlai, et al.An implement of ant colony optimization based on spark[J].Journal of computer applications, 2015, 35(10): 2777–2780.

[14]朱继召, 贾岩涛, 徐君, 等. SparkCRF: 一种基于 Spark 的并行CRFs算法实现[J]. 计算机研究与发展, 2016, 53(8):1819–1828.ZHU Jizhao, JIA Yantao, XU Jun, et al. SparkCRF: a parallel implementation of crfs algorithm with spark[J]. Journal of computer research and development, 2016, 53(8):1819–1828.

[15]DENG C, TAN X, DONG X, et al. A parallel version of differential evolution based on resilient distributed datasets model[C]//Bioinspired Computing-Theories and Applications. Springer, Berlin, Heidelberg, 2015: 84–93.

[16]TEIJEIRO D, PARDO X C, GONZÁLEZ P, et al. Implementing Parallel Differential Evolution on Spark[C]//European Conference on the Applications of Evolutionary Computation. Springer International Publishing, 2016:75–90.

[17]王虹旭, 吴斌, 刘旸. 基于Spark的并行图数据分析系统[J]. 计算机科学与探索, 2015, 9(9): 1066–1074.WANG Hongxu, WU Bin, LIU Yang. Parallel graph data analysis based on spark[J]. Journal of frontiers of computer science and technology, 2015, 9(9): 1066–1074.

[18]刘志强, 顾荣, 袁春风, 等. 基于SparkR 的分类算法并行化研究[J]. 计算机科学与探索, 2015, 9(11): 1281–1294.LIU Zhiqiang, GU Rong, YUAN Chunfeng, et al. Parallelization of classification algorithms based on sparkR[J].Journal of frontiers of computer science and technology,2015, 9(11): 1281–1294.

[19]袁斯昊, 邓长寿, 董小刚, 等. 求解大规模优化问题的云差分进化算法[J]. 计算机应用研究, 2016, 33(10):2949–2953.YUAN Sihao, DENG Changshou, DONG Xiaogang, et al.Cloud computing based differential evolution algorithm for large-scale optimization problems[J]. Application research of computers, 2016, 33(10): 2949–2953.

[20]董小刚, 邓长寿, 袁斯昊, 等. MapReduce模型下的分布式差分进化算法[J]. 小型微型计算机系统, 2016, 37(12):2695–2701.DONG Xiaogang, DENG Changshou, YUAN Sihao, et al.Distributed differential evolution algorithm based on mapreduce model[J]. Journal of Chinese computer systems,2016, 37(12): 2695–2701.

[21]谭旭杰, 邓长寿, 董小刚, 等. SparkDE: 一种基于RDD云计算模型的并行差分进化算法[J]. 计算机科学, 2016,43(9): 116–119.TAN Xujie, DENG Changshou, DONG Xiaogang, et al.SparkDE: a parallel version of differential evolutionbased on resilient distributed datasets model in cloud computing[J]. Computer science, 2016, 43(9): 116–119.

[22]ZAHARIA M, CHOWDHURY M, DAS T, et al. Resilient di-stributed datasets: a fault-tolerant abstraction for inmemory cluster computing[C]//Proceedings of the 9th USENIX conference on Networked Systems Design and Implementation. USENIX Association, 2012: 2–2.

[23]DAS S, SUGANTHAN P N. Differential evolution: a survey of the state-of-the-art[J]. IEEE transactions on evolutionary computation, 2011, 15(1): 4–31.

[24]王贤伟, 戴青云, 姜文超, 等. 基于Mapreduce的外观设计专利图像检索方法[J]. 小型微型计算机系统, 2012,33(3): 626–632.WANG Xianwei, DAI Qingyun, JIANG Wenchao, et al.Retrieval of design patent images based on mapreduce model[J]. Journal of Chinese computer systems, 2012,33(3): 626–632.

[25]YAO X, LIU Y, LIN G. Evolutionary programming ma-de faster[J]. IEEE transactions on evolutionary computation,2000, 3(2): 82–102.

[26]WANG Y, CAI Z, ZHANG Q. Enhancing the search ability of differential evolution through orthogonal crossover[J]. Information sciences, 2012, 185(1): 153–177.

[27]范德斌, 邓长寿, 袁斯昊, 等. 基于MapReduce模型的分布式粒子群算法[J]. 山东大学学报: 工学版, 2016, 46(6):23–30.FAN Debin, DENG Chanshou, YUAN Sihao, et al. Distributed particle swarm optimization algorithm based on mapreduce[J]. Journal Shandong university: engineering science, 2016, 46(6): 23–30.

[28]TAGAWA K, ISHIMIZU T. Concurrent differential evolution based on MapReduce[J]. International journal of computers, 2010, 4(4): 161–168.