二维声波方程交错网格有限差分数值模拟研究

杨晓柳，竺 俊，姚 铭，桂志先

(1. 长江大学 油气资源与勘探技术教育部重点实验室，湖北 武汉 430100； 2. 长江大学 地球物理与石油资源学院，湖北 武汉 430100； 3. 中石化西北油田分公司采油一厂，新疆 轮台 841600)

0 前 言

在地震勘探领域中，人们常常利用地震波场数值模拟技术研究地震波的传播机理。地震数值模拟就是提前给定地下介质模型和相应物理参数，模拟地震波在地下介质中的传播过程，并对地面或地下各个观测点观测到的数值地震记录进行计算分析的一种地震模拟方法。地震数值模拟方法在地震勘探和天然地震领域得到了普遍地推广使用，在地震数据采集、处理和解释的各个环节都发挥着重要作用。

地震波场数值模拟方法主要包括有限差分法、有限元法、伪谱法等[1]，其中有限差分法是利用 Taylor 展开式来近似代替波动方程中的微分，使微分形式的波动方程变成差分形式，来用于求解波动方程。他具有占有内存小、计算速度快，编程相对简单等优点[1]，是最常用的地震波场数值模拟方法之一。本文通过建立地质模型，利用Matlab语言进行编程，完成了声波方程交错网格有限差分算法的数值模拟。通过模拟声波在不同介质中的传播过程，对比分析不同时刻、不同介质的波场快照，深入理解地震波在不同介质中的传播规律。有限差分算法在模拟精度和模拟计算速率方面都展现出一定优势。综上所述，地震波场数值模拟对于人们深入研究地震波的传播规律，准确解释实际勘探中的地震资料等均具有重要的理论和实际意义。

1 声波方程及其交错网格有限差分格式

在实际的地震勘探过程中，最常用到的数值资料是纵波资料。因此讨论利用声波方程来进行地震波的模拟。有限差分法是基于差分原理的一种数值计算方法。其基本思想是：将求解区域网格化，应用差分原理，用差商来近似的代替微商，将求解连续函数的问题转化为求解网格节点上的差分方程组的问题，得到数值解。在波动方程网格离散化的过程中，可以利用交错网格的差分形式。

1.1 均匀各向同性介质二维声波方程

均匀各向同性介质二维声波方程可表示为：

(1)

其中，u(x,y,z,t)为地表记录的压力波场或位移波场，v(x,z)为声波速度场。

1.2 非均匀介质中二维声波方程

非均匀各向同性介质中二维声波方程的一阶应力—速度方程形式如下：

(2)

其中，vx，vz是质点速度，u是法线应力，ρ是密度，vp是纵波速度。

1.3 交错网格有限差分

在对介质模型进行离散化处理的过程中，网格是一种常用手段。对波动方程进行网格离散，可以利用交错网格的差分形式。交错网格就是把速度和应力分配到两套不同的网格中，这样可以使速度、应力得到很好的耦合[2]。利用交错网格有限差分法对一阶速度—应力波动方程进行求解时，应力、速度等分量在模型交错网格节点中的位置分布如图1所示。

图1 交错网格剖分

其中三角形为τxx，τzz，四边形为τxz，圆形位于个立方体中心为vx，六边形为τz。

利用Taylor级数展开法，把波动方程中的导数用网格节点上的函数值的差商近似代替，进行离散；推导出了时间域2阶、空间域2N阶精度的交错网格离散差分格式。

速度水平分量：

速度垂直分量：

应力Pxx：

应力Qzz：

应力Sxz：

2 有限差分数值模拟中的关键技术及解决方案

2.1 模拟震源

正演模拟中有一个重要的部分就是加载震源。需要加载震源，震源的加载方式以及类型等因素，都能影响正演模拟的结果。本文选择的是雷克子波作为加载的震源，来模拟激发地震波。雷克子波是零相位的，零相位子波可以达到分辨率的极限[1]。

雷克子波表达式(时间域)为：

(3)

通过傅立叶变换为频率域：

(4)

其中，初始时刻是t0，主频是fM。我选用频率为40 Hz，然后采用时间域的雷克子波的公式做成图，如图2所示，该图为本文在进行地震波场数值模拟时才采用的雷克子波波形。

2.2 边界条件

在进行数值模拟的过程中，计算机的内存是有限的，无法做到模拟一个无限大的介质区域，都会存在一定的范围限制，即存在一定的边界，这就是我们所说的人为边界。而在实际情况下，真正的地下介质类似于半无限大的空间。因此，在有限的计算区域内，地震波在传播过程中若遇到人工边界就会产生边界反射，这些来自边界上的边界反射波会对计算区域的波场值造成干扰，产生边界效应，严重降低地震波数值模拟结果的准确性。因此在进行波场模拟的时候。引入恰当的边界条件是十分重要的[3]。

图2 主频为40 Hz的雷克子波的特征

为了尽量降低人为边界所产生的影响，我们可以引入恰当的边界条件来更加真实的模拟无限的实际空间，尽最大可能去削弱边界反射，改善正演模拟的效果。

许多学者进行了相关方面的研究，提出多种构造边界的方法。Clayton和Engquist[4]在1977年提出了一组包含不同阶数的吸收边界条件(简称 CE)。Reynolds[5]在1978年通过分解波动方程提出了透明边界条件(简称TBC)。Berenger[6]在1994年针对电磁波的传播，提出了PML(完全匹配层)吸收边界条件，并从理论上证明了利用PML边界条件可以吸收任一频率、任一方向的电磁波。Frank，Hastings 等[7]在1995年将PML的算法思想成功地应用于对弹性波的模拟中。

1)透明边界条件

(5)

2)Clayton-Engquist 边界条件

Clayton和Engquist 提出的一组包含不同精度的吸收边界条件，其中如下的二阶近似边界条件应用最为普遍[4]。

(6)

为了测试边界条件的作用，本文在此利用一个均匀介质模型，模型的区域大小为1 000 m×1 000 m，震源位于(500 m，500 m)处，计算网格大小为5 m×5 m，时间采样率为0.5 ms，总采样时间为0.2 s，速度采用3 500 m/s，子波频率为40 Hz。

采用交错网格有限差分算子对拥有边界条件跟无边界条件的情况分别进行模拟，得到t=200 ms时的波场快照，如图3所示。

图3 均匀介质模型下有无边界条件在t=200 ms的波场快照

由图3可知，使用了边界条件的波场快照在边界处边界反射波得到明显的削弱，而没有进行边界处理的边界反射波很明显。通过引入恰当的边界条件，可以有效地削弱边界反射。

2.3 稳定性

由于波动方程的有限差分格式一般都是按时间递推的，因此前一时间波函数值的舍入误差必然会对后一时间的波场产生影响。这就需要对误差传播和积累的情况进行了解，使误差不至于随时间的推进而快速累积，破坏整个数值解，影响数值模拟的效果，严重时还可能导致计算溢出，使得数值模拟无法继续进行。因此稳定性问题成为有限差分格式无法忽略的一个基本问题。根据Lax等价定理[8]，在保证稳定性的同时，也就保证了差分格式的收敛性。

稳定性问题是有限差分法正演模拟中不可忽略的问题之一。每进行一次波场模拟，都要分析稳定性的问题。一般来说，随着时间的推移，如果误差不增加，那么这个差分格式可以认为是符合稳定性条件的。

针对均匀介质，显式的稳定性条件可以由谱分析得到：

(7)

其中，vz是纵波速度，可见上式与横波速度vx无关。令Δx=Δz，则稳定性条件为：

(8)

常规差分方程其稳定性条件为：

(9)

因为vx

(10)

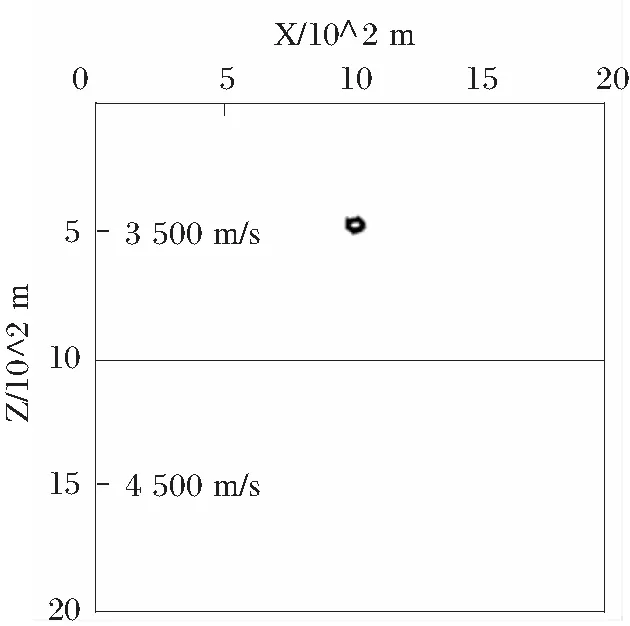
2.4 数值频散问题

数值频散是有限差分法最大的缺点。在用有限差分进行数值模拟的过程中，常常会观察到，一些同相轴的形状随着时间的推移逐渐变化，有的还逐渐分散，由一根同相轴分裂为许多根同相轴，这种现象是由于波传播相速度和群速度不一致所导致的，我们称该现象为数值频散现象[9]。数值频散在实质上是由于在数值计算过程中离散网格而产生的一种伪波动，这种频散在差分方程求解波动方程的过程中是无法避免的。

在有限差分正演模拟过程中，当一个波场内采样点太少时，用差分逼近微分的过程中就会产生较大的误差，就会产生数值频散[10]。在给定地震子波频率的情况下，若速度越低，一个波场内的网格点数就越少，频散就越严重；在给定空间网格间距的情况下，子波的频率越高，一个波场内的网格点数就会越少，数值频散也越严重。因此，在进行数值模拟时，提高差分阶数，减少网格步长和降低地震子波频率是减弱频散现象最有效的方法。

本文通过建立一个均匀介质模型，通过改变网格步长和子波频率，利用有限差分算法进行数值模拟，得到波场快照如图4～5所示。

图4 网格步长为5 m(左)与网格步长为6 m(右)波场快照

图5 不同主频波场快照

图4与图5表明随着网格步长和子波主频的增加，频散现象越来越严重。即可以通过适当减小网格步长和子波主频来压制频散现象。

3 有限差分数值模拟实例

3.1 均匀介质模型

模型大小为1 000 m×1 000 m,空间步长为5 m，速度采用3 500 m/s(图6)，震源位于模型(500 m，500 m)处，采用雷克子波作为震源，其主频为40 Hz，满足弹性波数值模拟的稳定性条件，对声波方程利用交错网格有限差分进行数值模拟，总采样时间为0.2 s。均匀介质模型如图6所示。

图6 均匀介质模型

模拟结果如图7所示。

图7 均匀介质模型在不同时刻得到的波场快照

图7可以看出，波场快照中的同相轴是圆形的，说明在均匀各向同性介质中，点源激发的波前面是一个圆，这与理论也是吻合的。并且随着时间的增大，波前面的面积逐渐增大，说明地震波从震源中心向外传播。

3.2 双层介质模型

模型大小为2 000 m×2 000 m，空间步长为5 m，上层介质速度为35 000 m/s，下层介质速度为4 500 m/s(图8)，震源位于模型(1 000 m，500 m)处，采用雷克子波作为震源，其主频为40 Hz。对声波方程利用交错网格有限差分进行数值模拟，总采样时间为0.2 s。双层介质模型如图8所示。

图8 双层介质模型

模拟结果如图9所示。

图9 双层介质模型不同时刻的波场快照

图9中可以看出，在未遇到界面前，地震波在均匀介质中的波前面一个圆。当地震波入射到两种不同介质的分界面时，会产生透射波和反射波，符合波动理论。

4 结 论

1)针对数值模拟过程中存在的边界反射问题，可以通过引入恰当的边界条件来解决，尽最大可能去削弱边界反射，改善正演模拟的效果。

2)空间采样间隔越大，计算速度越快，相应的数值频散现象越严重，因此，要合理选择空间步长，以便同时兼顾抑制频散和提高计算效率。

3)震源子波频率对模拟效果也有一定的影响。子波频率越高，分辨率也会越高，但数值频散现象也越严重，因此需要合理选择震源子波的主频，在保证具有较高分辨率的同时可以充分压制数值频散。

4)对不同时刻波场快照分析说明，利用声波波动方程计算地震波场具有很好的运动学和动力学特征。为深入了解地震波在地下介质中地震波传播规律的研究提供理论依据。

[1] 冯英杰, 杨长春, 吴萍. 地震波有限差分综述[J]. 地球物理学进展, 2007, 22(2): 487-491.

[2] 王毓军. 二维地震波场有限差分正演模拟及合成地震记录的实现[D]. 桂林: 桂林理工大学, 2011.

[3] 梁超, 吕力行, 童祥轩. 采空区顶板动力响应数值模拟研究[J]. 中国锰业, 2016, 34(4): 61-67.

[4] Robert C, Born E. Absorbing boundary conditions for acoustic and clastic wave equation[J]. Bulletin of the Scismalagical Society of America, 1977, 66(11): 1529-1540.

[5] Reynolds A C. Boundary conditions for the numerical solution of wave propagation problems[J]. Geophysics, 1978, 43(6): 1099-1110.

[6] Jean-pierre B. A perfectly matched layer for the absorption of electromagnetic waves[J]. Jouenal of Computational physics, 1994(114): 185-200.

[7] Hastings F D, Schneider J B. Application of the perfectly matched layer[J]. Journal AcousricalSociety of America, 1996, 100(5): 3051-3068.

[8] 倪长宽. 复杂介质地震波场正演模拟方法研究[D]. 青岛: 中国石油大学, 2008.

[9] 刘庆敏. 高阶差分数值模拟方法研究[D]. 青岛: 中国石油大学, 2007.

[10] 李胜军. 地震波数值模拟中的频散压制方法分析[J]. 石油物探, 2008, 47(5): 444-449.