抑制配电网谐波影响的新型相位检测方案
2018-03-14贝太周侯志刚
贝太周 ,杨 凯 ,侯志刚 ,李 莎 ,张 芳
(1.国网山东省电力公司济南供电公司,山东 济南 250012;2.国网山东济南市长清区供电公司,山东 济南 250300)
0 引言
电力系统核对相位是配电网运行检修中的常规工作。传统的核相方法多数采用电压互感器或高压验电器,而前者设备笨重,后者依靠微弱的辉光指示容易出现误判断。由于核相仪具有很强的抗干扰性,符合EMC标准要求,兼有重量轻、便于携带等优势,已经成为配电网运维检修工作中常见的用于相位校验和相序校验的量测设备,具有核相、测相序和验电等功能。传统的核相仪通过采集器实时采集配电网电压数据,从中取出被测高电压的相位信号,经过处理后直接发出,由核相仪的其他功能部件接收并进行相位比较,完成核相功能。所以核相仪的测量精度很大程度上取决于采集器的输出精度。
很多相位检测方案在近几年被相继提出。这些检测方案大体上可以分为两类:一类是以离散傅里叶变换(discrete Fourier transform,DFT)、递归的离散傅里叶变换 (recursive discrete Fourier transform,RDFT)以及滑动平均滤波器(moving average filters,MAFs)等方法为主的开环方案;另一类则是以锁相环(phase-locked loop,PLL)为主的闭环方案[1]。
在开环方案中,DFT技术被用于对电网波形的频谱分析,时变条件下通常会引起频谱泄漏[2]。在滤波性能方面,DFT仅对整数次谐波具有良好的滤除效果,而对间谐波的滤波能力则表现不佳。RDFT技术可以有效降低传统DFT的运算量,但是容易产生相角输出的累积误差[1-2]。MAFs是一种有限脉冲响应滤波器,可以有效滤除周期为窗口宽度内整数值的所有谐波,但在时变条件下会产生时间延迟[3]。闭环方案是一种无差输出的闭环反馈控制系统。在电力电子及电力系统领域,基于PLL实现的相位检测方案备受欢迎并且得到广泛应用[4]。即便在谐波扰动严重的电网环境下,PLL同样可以实现对电网相位的检测。
未来配电网将会高比例接入清洁可靠和产能灵活的可再生分布式电源,分布式电源中的并网逆变器等大量非线性负载不可避免地对配电网产生较为突出的谐波污染[5-6]。为了准确获得配电网电压的相位信息,必须保证核相仪能够在谐波畸变的电网环境中仍然保持较高的检测精度[7]。
目前针对谐波扰动的相位检测方案在近期文献中被不断提出。借助复数滤波器进行多通道谐波解耦及补偿在近期文献中备受推崇[6,8]。此种方法的核心在于对电网环境中存在较多的某次谐波分通道地进行无衰减提取,然后将提取到的谐波反馈补偿到电网电压采样信号中,即对某一谐波采取“先提取后补偿”的方式进行高效抑制。然而这类方法仅适用于谐波组成相对稳定的电网环境,当电网谐波畸变严重时,谐波抑制性能将大为受损。尽管可以通过添加通道数目的方法来加以改善,但是此种方法无疑又会增加系统实现的复杂度[9]。因此,如何保证滤波器能够在谐波畸变严重的电网环境下最大频率范围地抑制谐波是滤波器设计和实现时必须要考虑的问题。
以单相系统为应用背景,以传统锁相环结构为基础,研究一种能够有效抑制配电网谐波影响的新型相位检测方案。首先提出一种新型的自适应陷波滤波器,然后将该滤波器应用在锁相环结构的前级,实现对配电网谐波的有效抑制,从而最终消除谐波对相位检测结果的影响。最后对所提方案的可行性和有效性通过仿真进行验证。
1 基于PLL的单相电网电压相位检测方案
图1给出了在传统同步旋转坐标系下基于比例—积分 (PI)反馈控制实现的单闭环PLL结构框图。通常来讲,所有的PLL结构均由鉴相器(PD)、环路滤波器(LF)和压控振荡器(VCO)3个模块构成[10]。图 1 中,ωff为 VCO 的中心频率,其值取决于所测频率的范围。

图1 传统PLL结构
在具体实现上,三相应用场合中借助Clark变换即可得到αβ坐标系下的电压vα和vβ,而在单相应用场合,往往需要根据输入的单相电网电压构造与之正交的虚拟电压信号。
假设单相电网电压为

式中:V和ω分别为单相电网电压的幅值和基波角频率。
根据图1中鉴相器的相移因子e-j90°,可以构造虚拟正交电压为

这样,就得到了单相PLL方案所需要的电压vα和 vβ,即

然后利用基于同步旋转坐标变换的三相锁相环原理即可获取单相电网电压的相位。
值得一提的是,上述结论是在不考虑电网中的谐波扰动情况下得出的。在实际的电网环境下,不可避免地含有电网谐波。研究发现,当电网中存在谐波扰动时,将会为dq坐标系下的电压分量vd带来谐波干扰,最终影响相位检测的准确性[11]。
2 自适应陷波滤波器
从设计成本和功能考虑,滤波器设计和实现时必须要关注的问题是保证滤波器在结构简单和大频率范围谐波抑制两方面的兼顾。
自适应陷波滤波器的频域传递函数为

式中:k和ω分别为陷波滤波器的阻尼系数和中心频率。为了保证陷波滤波器能够时刻跟随实际的电网频率,ω将受电网频率的调制。

图2 自适应陷波滤波器的Bode图
图 2 给出了在 k=0.1,ω=2π50 rad/s时自适应陷波滤波器的Bode图。由图2可知,自适应陷波滤波器仅对输入信号中的基频信号有很强的抑制作用,对其他非基频信号的抑制作用不明显。因此,当陷波滤波器的输入电网电压信号如式(5)所示时,

得到的输出信号可以表示为

式中:n为电网谐波的谐波次数。
若将式(5)和式(6)做差,便可得到电网电压中的基频信号,相应地,也就有效抑制了电网电压中的谐波扰动。基于这一考虑,提出的滤波方案如图3所示。
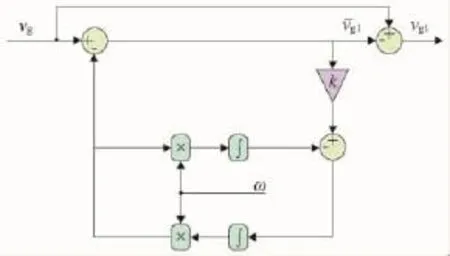
图3 自适应陷波滤波方案
自适应陷波滤波器的阻尼因子k同时影响着自身的滤波性能和动态响应性能,因此在取值时应当实现两者的兼顾[12],本文选取 k=0.1。
3 整体方案实现
新型相位检测方案的整体方案如图4所示。
为了简单实现虚拟电压的构建,在PLL中,引入式(7)所描述的全通滤波器(All Pass Filter,APF)结构。

式中:ω为APF的中心频率。为了保证APF能够在时变条件下产生与电网基频信号相正交的虚拟电压,ω同样受电网频率的调制。
4 仿真实验验证

图4 整体方案的实现
为了验证所提相位检测方案的响应性能,仿真实验中用10 V/50 Hz的交流信号来模拟实际电网中基频信号。谐波信号按照表1给出的数据取值[13]。图5给出了自适应陷波滤波方案的仿真结果。

表1 谐波抑制测试中注入的谐波含量及THD
由图5可知,当电网电压中含有较高的谐波扰动时,借助所提出的自适应陷波滤波方案,可以很好地抑制电网中的谐波扰动,从中获得具有较高正弦度的基频信号。

图5 自适应陷波滤波输出波形
在获得较高正弦度的基频信号后,在PLL环节中得到的正交电压vα和vβ的波形如图6所示。从图中看出,在vα基础上,借助APF,同样可以获得具有较高正弦度的虚拟电压vβ。
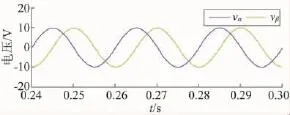
图6 采用滤波方案后获得的正交电压波形
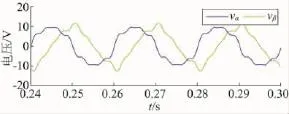
图7 未经滤波处理的APF输出电压波形
为了体现图4中滤波方案的重要性,图7给出了在不经滤波处理时,含有谐波的电网电压直接经APF得到的虚拟电压波形。很明显,此时的电压vα和vβ均含有大量的谐波,同时无法正交。在此条件下,得到的相位检测波形如图8所示。

图8 未经滤波处理时的相位检测结果

图9 经本方案得到的相位检测结果
当采用本文所提方案时,得到的相位检测波形如图9所示。比较图8和图9的仿真结果可以得出,当采用本文所提方案时,电网电压中的谐波被自适应陷波滤波器有效抑制,大大提高了相位检测的准确性。原因在于,如果电网电压中的谐波未经滤波处理,经过坐标变换后,会在dq坐标系下的电压分量vd中产生2倍频的谐波干扰,从而影响相位检测的准确性。这一点,可从图10中的仿真波形中得到验证。

图10 电压分量vd的仿真波形
5 结语
为了保证相位检测的准确性不受配电网谐波的影响,提出了一种能够抑制配电网谐波影响的新型相位检测方案。该方案是在传统锁相环的前级引入由自适应陷波滤波器建立的预滤波单元来实现的,具有结构简单、参数设置少和动态性能好等突出优点。方案的可行性和有效性通过仿真实验得以验证。
[1]BARADARANI F,ZADEH M R D,ZAMANI M A.A phase-angle estimation method for synchronization of grid-connected powerelectronic converters[J].IEEE Transactions on Power Delivery,2015,30(2):827-835.
[2]REZA M S,CIOBOTARU M,AGELIDIS V G.Accurate estimation of single-phase grid voltage parameters under distorted conditions[J].IEEE Transactions on Power Delivery,2014,29(3):1138-1 146.
[3]JORGE S G,BUSADA C A,SOLSONA J A.Frequency adaptive discrete filter for grid synchronization under distorted voltages[J].IEEE Transactions on Power Electronics,2012,27(8):3584-3594.
[4]GOLESTAN S,MONFARED M,FREIJEDO F D,et al.Advantages and challenges of a type-3 PLL [J].IEEE Transactions on Power Electronics,2013,28(11):4 985-4 997.
[5]VAZQUEZ S,SANCHEZ J A,REYES M R,et al.Adaptive vectorial filter for grid synchronization of power converters under un balanced and /or distorted grid conditions[J].IEEE Transactions on Industrial Electronics,2014,61(3):1 355-1 367.
[6]MATAS J,CASTILLA M,MIRET J,et al.An adaptive prefiltering method to improve the speed/accuracy tradeoff of voltage sequence detection methods under adverse grid conditions[J].IEEE Transactions on Industrial Electronics,2014,61(5):2 139-2 151.
[7]杜雄,王国宁,孙鹏菊,等.两相静止坐标系下消除不对称和谐波影响的同步信号提取方法[J].电工技术学报,2015,30(4):249-256.
[8]RODRíGUEZ P,LUNA A,CANDELA I,et al.Multiresonant frequency-locked loop for grid synchronization of power converters under distorted grid conditions[J].IEEE Transactions on Industrial Electronics,2011,58(1):127-138.
[9]RODRíGUEZ P,LUNA A,MUN~OZ-AGUILAR R S,et al.A stationary reference frame grid synchronization system for threephase grid-connected power converters under adverse grid conditions[J].IEEE Transactions on Power Electronics,2012,27(1):99-112.
[10]GOLESTAN S,MONFARED M,FREIJEDO F D,et al.Dynamics assessment of advanced single-phase PLL structures [J].IEEE Transactions on Industrial Electronics,2013,60(6):2 167-2 177.
[11]GHARTEMANI M K,KHAJEHODDIN S A,Jain P K,et al.Addressing DC component in PLL and notch filter algorithms [J].IEEE Transactions on Power Electronics,2012,27(1):78-86.
[12]GOLESTAN S,MONFARED M,FREIJEDO F D,et al.Performance improvement of a pre-filtered synchronous reference frame PLL by using a PID-Type loop filter[J].IEEE Transactions on Industrial Electronics,2014,61(7):3 469-3 479.
[13]REZA M S,CIOBOTARU M,AGELIDIS V G.Robust technique for accurate estimation of single-phase grid voltage fundamental frequency and amplitude[J].IET Generation,Transmission&Distribution,2015,9(2):183-192.
