多指标FCM 聚类算法在风电场聚类问题中的应用

李观阳 ，刘洪正 ，李广磊 ，孙 毅 ，刘志敏

（1.山东理工大学，山东 淄博 255000；2.国网山东省电力公司电力科学研究院，山东 济南 250003；3.山东中实易通集团有限公司，山东 济南 250003）

0 引言

风力发电是新能源发电中最有前景的技术之一，风电具有大规模、集中接入的特点，而且风电场的装机容量在逐年提高，因此研究风电场的等效模型日趋必要。目前针对风电场模型建立的问题，主要是采用K-means算法对风电机组进行聚类，但该算法有一定的局限性，且采用某一聚类指标，通常是单一的风速，单一的风机功率等作为聚类指标。

目前针对风电场模型的建立方法主要包括：单机等值模型［1］，将单台风机的参数等价成整个风电场的参数，与详细模型的误差比较大；多级等值模型［2-3］，相对于单机模型更加准确；根据风速功率建立模型或者转速向量建模［2-5］，使用TWO-Step分别以风速和转速向量作为评价指标进行聚类［1］，具有其片面性；根据风机的有效输出功率序列［6-7］，建立等效的风速与功率的序列对，采用试探法，计算非常复杂。以上风电场多机等值模型的建立都未对所选的聚类算法的准确性进行考虑。针对此问题本文提出了适用于建立风电场多机等值模型的多指标FCM聚类算法，采用多种风电场外特性指标进行聚类，并分别对风电场的稳态特性、故障响应与风电场的详细模型进行了比较，验证了FCM算法在处理风电机组聚类问题上的优越性。

1 聚类指标选择

1.1 风—功率

风速具有波动性，难以预测性，由于风能的尾流特性，各台风机获得的风能不同。不同的风速条件下风机的出力并不严格按照功率特性曲线变化，而是分布在曲线周围。再加上地形、阵风、发电机控制系统时滞效应等因素的影响，给风电场模型的建立带来了很大的困扰。双馈型风力发电机采用变桨距调节方式，使桨距角具有可控性，在风速超过额定值运行时具有较高的稳定性，输出功率稳定在额定值附近。风能利用系数近似表示为

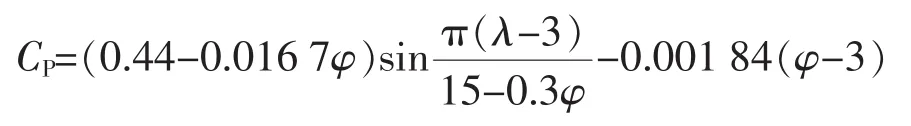
式中：λ为叶尖速比；φ为桨距角。采用变桨距模式的1.6 MW风力机的功率特性计算曲线如图1所示。

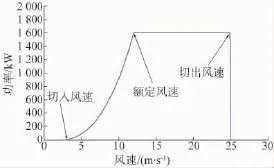
图1 1.6 MW DFIG风力机出力

由图1可知，当风速大于额定风速时，风力机的计算功率会比较稳定，然而其实际功率与计算值有一定偏差。所以仅仅以风速或者按照风力机的功率当作聚类指标，都是有很大缺陷的。因此，考虑将风速、风力机的功率都作为聚类指标。

1.2 风电机组转子转速

风电场的暂态特性是研究风电场模型必须考虑的部分，因此需要提取风电机组的暂态特性作为聚类标准。双馈型风力发电机组DFIG（Double Fed Induction Generator）的定子侧与电网直接相连，当电网发生短路故障导致电压跌落时，为了维持定子侧的磁链不发生变化，定子侧电流迅速增加，同时在转子侧感应出过电流，导致转子转速迅速增加，如图2所示。

在5 s时风电场并网点设置三相短路，6 s故障清除。故障清除后转子转速逐渐恢复正常，其恢复速度代表了该风电机故障穿越的能力。选取故障清除0.4 s后转子的转速ω作为聚类指标。

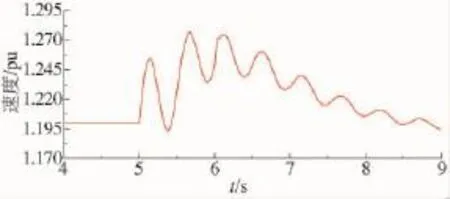
图2 双馈型风力发电机转子转速

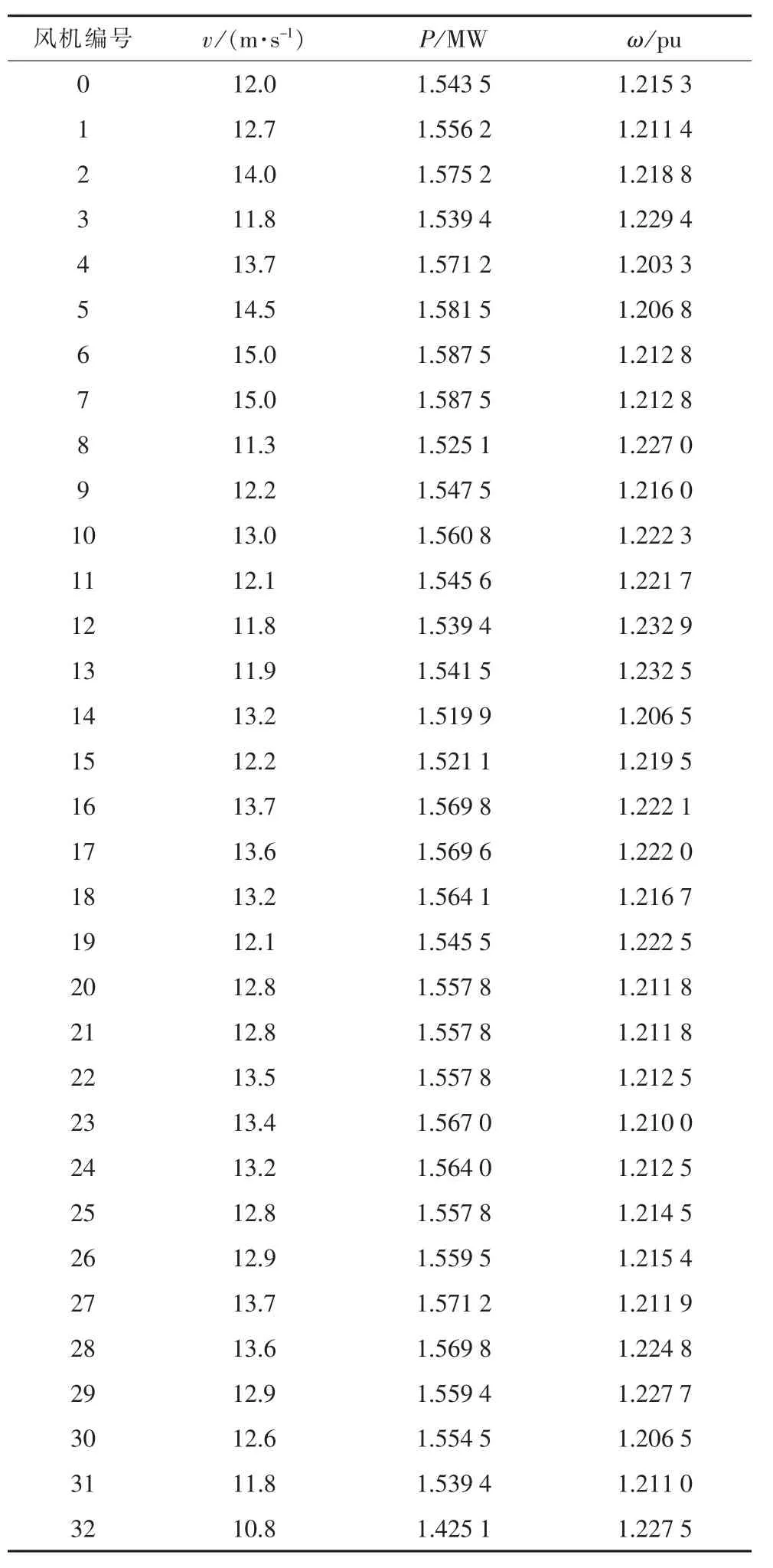
表1 风速、风机功率、转速

1.3 数据获取

传统的聚类指标一般选取风速、功率、转速等单一指标作为聚类标准，本文选取了东源风电场2017-04-02的风速数据， 并对 09∶00-10∶00的风速数据进行采样，采样间隔为10 min，并最后做均值处理，通过在Digsilent/Power Factory平台上搭建东源风电场的详细模型，v为嵌入风速数据，P为获取风力机功率，ω为短路故障清除后转子转速数据，具体数值如表1所示。

2 聚类算法对比分析

2.1 K-Means聚类算法

K-means聚类算法是一种“硬”聚类算法，根据数据性质严格地将其归在某类中，该方法在处理蝶形数据时有很大的缺陷，相同的数据，聚类中心的选取不同，在运行程序时会被归在不同的类别，容且易陷入局部最优解［8］，故本文放弃了传统的K-Means聚类算法。

2.2 FCM聚类算法

FCM是一种基于划分的聚类算法，又称为模糊C—均值算法，是一种“软”聚类。其原理是使划分到同一簇的相似度最大，不同簇的对象相似度最小，用隶属度确定某个对象隶属于某个簇的一种聚类算法，隶属度一般用u来表示，该聚类算法有模糊划分和很强的柔韧性特点。

FCM聚类算法是一种求目标函数极值的过程，设待聚类的风机有n台，每一台用xi表示，xi中包含了第台风机的风速、有功功率、转速。功率风机的需要将其聚成c类，那么我们就需要c个聚类中心，聚类中心用ci表示 （聚类中心可以不是确切的风机数据），uij表示第j台风机属于第i类的隶属度，其中0＜uij＜1，定义FCM的目标函数及约束函数为

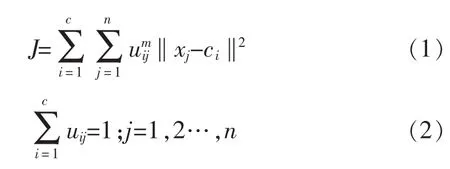
式中：m为加权指数，通常取1.5～2.5之间的数值，本文加权指数取2；‖xj-ci‖为第j个样本风机与第i个聚类中心的欧氏距离。为求得目标函数在有约束条件下的最小值，根据拉格朗日数乘法，构造一面的函数为

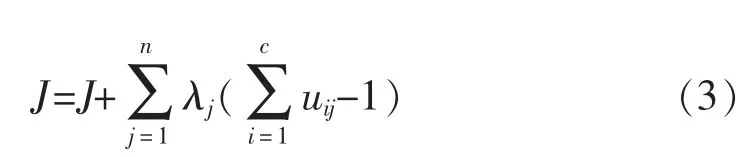
使得

可求得使（1）式取最小值时的必要条件为

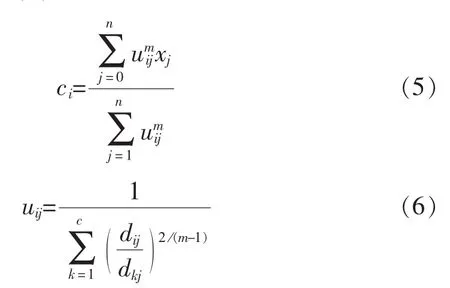
根据上述原理可知，模糊聚类即为不断更新不断迭代的过程，并根据

判断是否成立来决定迭代过程的结束，具体过程如图3所示。

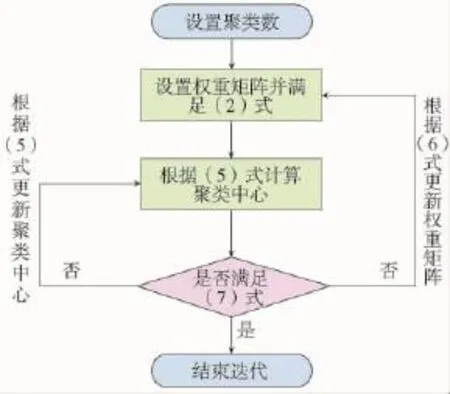
图3 FCM聚类过程

聚类前数据分布及聚类后结果如图4、图5所示。

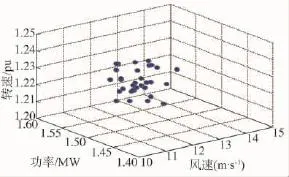
图4 聚类前数据点

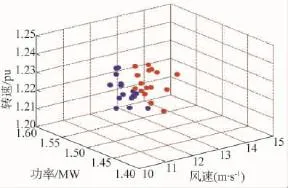
图5 FCM聚类结果

2.3 AP聚类算法

AP聚类算法全称仿射传播聚类算法（Affinity Propagation），是2007年在Science杂志上提出的一种新的聚类算法，具有很多其他算法望尘莫及的优势，包括聚类中心为确切的样本数据，不需事先指定类的个数，对初值的选取不敏感，对距离矩阵的对称性无要求等。

首先介绍此类算法中常用名词。Exemplar：聚类中心。Similarity：风机 i和风机 j的相似度，记为 s（i，j）。一般相似度 s（i，j）选取欧氏距离计算为

式中：vi为第i台风机获取的风速；Pi为第i台风机的输出功率；Vi为第i台风机转子转速。Preference：风机 i的参考度，记为 P（i）或 s（i，i），P（i）是指点作为聚类中心的参考度,s（i，i）一般取相似度值的中值。Responsibility：用来描述风机k适合作为风机i的聚类中心的程度，记为 r（i，k）。 Availability：用来描述风机i选择风机k作为其聚类中心的适合程度，记为a（i，k）。 Damping factor：阻尼系数，主要起收敛作用。

风机聚类为不断迭代的过程，迭代的过程主要更新两个矩阵，代表矩阵 R［r（i，k）］N×N和适选矩阵A［a（i，k）N×N］。 这两个矩阵通过不断的迭代才初始化为0，N为所有风机的数目。迭代更新公式为

迭代方法为

式中：λ为阻尼系数可以防止迭代震荡。聚类结果如图6所示。表2为两种聚类结果总结。

图6 AP聚类结果

表2 聚类结果

2.4 聚类方法选择

3种聚类算法在聚类之初都需要进行对数据进行除量纲化处理，即数据的标准化处理，一般选取标准差变换或者极差变换，本文选取的是极差变换，为

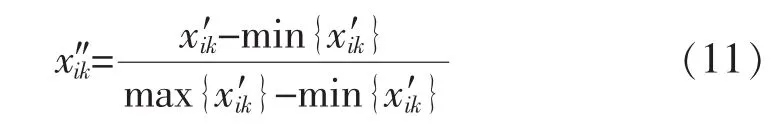
经过变换后保证所有数据都在［0，1］区间内，消除了量纲的影响。AP聚类算法不需要事前确定聚类的类数，自动求得最佳聚类数，但在本次聚类中发现，其聚类数过多，失去了建立风电场等效模型的意义，故采用FCM聚类算法更为合适。

3 等值模型的等效参数

3.1 风速等效

根据风力机输入风能相等的要求对该群等效风速设置为平均风速，在FCM聚类算法中风速分别为：机群一：v1-eq=11.4 m ／s；机群二：v2-eq=13.7 m ／s。

3.2 风力发电机及变压器等效

东源风电场有33台双馈型风力发电机，额定功率1.5MW，分布在3条馈线上，最后并于同一条35 kV母线上，并再次通过35／110 kV变压器并网。采取容量加权算法，将发电机与变压器等值为

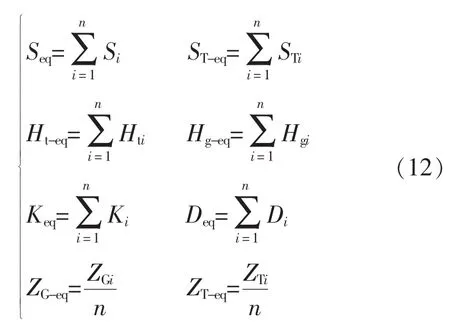
式中：Seq、ST-eq、Ht-eq、Hg-eq、Keq、Deq、ZG-eq、ZT-eq分别为风电场等效模型中的发电机额定容量、变压器额定容量、风力机惯性时间常数、发电机转子惯性系数、刚度系数、轴阻尼系数、发电机等效阻抗、变压器的等效阻抗；n为该等效机群的发电机台数；i为该机群的风机。

3.3 无功补偿装置及集电系统等效

风力发电厂均有无功补偿装置，一般采取集中补偿的方式，风力发电场的风机也都具有无功控制的能力，在机端都有无功补偿电容装置，能将功率因数控制在0.96以上，既要考虑单台无功调节能力又要考虑集中补偿装置的容量，最终采取等效其中C0为集中无功补偿装置的电容值。根据等值消耗功率法，集电系统的等效阻抗一般选取为

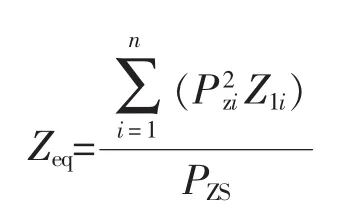
式中：Z1i为第i台风机所在线路支路的阻抗值；PZi为Z1i上消耗的电功率；PZS为流过等效阻抗的总功率；n为某风机群的台数。

4 仿真验证

东源风电场装机容量49.5 MW，由33台额定容量为1.5 MW的东汽双馈风电机组构成，场内共有3条35 kV集电线路。为验证该等效聚类算法的有效性，以东源风电场的详细模型作为标准模型，对等效模型的静态有功功率，故障状态下的无功反应及故障清除后有功恢复情况作了仿真研究，并与详细模型进行比较。功率的评价指标为

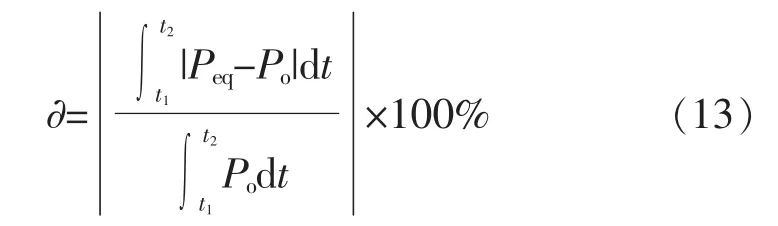
经过仿真，获取风电场有功功率与无功功率分别如图6~11所示。在风电场并网点10 s时刻设置持续1 s的三相短路故障，并网点电压跌落至0.3 pu避免风电机组脱机。对稳态和故障状态下的有功与无功进行了误差计算，误差计算结果如表3所示，根据FCM聚类算法建立的新模型风电场详细模型稳态有功输出误差只有0.02%，无功误差只有1.4%，故障恢复阶段分别为5%和1.8%，比传统单机模型的误差要小很多，能更准确反映风电场的稳态输出功率与故障特性，验证了模型的准确性。

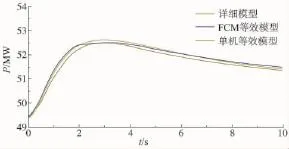
图7 有功功率0～10 s

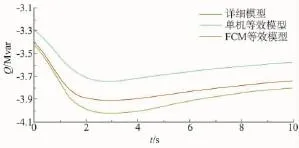
图9 无功功率1～10 s

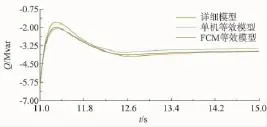
图10 无功功率11～15 s

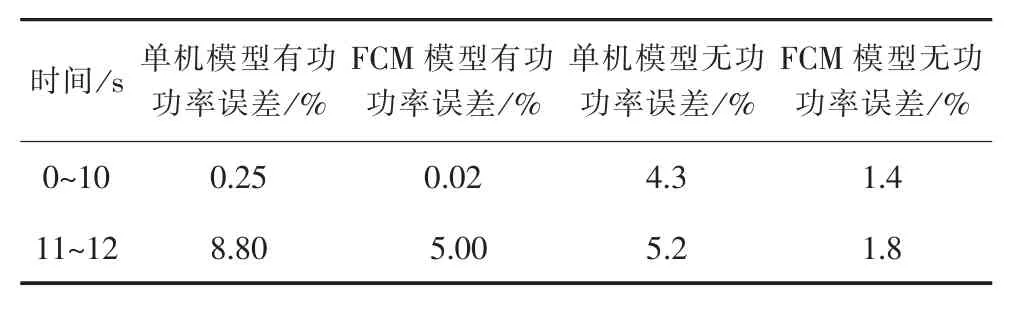
表3 模型误差分析

5 结语

对K-Means聚类、FCM聚类、AP聚类等算法进行了分析比较，最终选取了FCM算法作为聚类算法。提取了风速、风力机功率、转速向量作为聚类指标，并对聚类指标数据进行了除量纲处理。与传统的单机等效模型进行了比较，无论是稳态输出还是暂态输出，相应FCM聚类后的等效模型都更加准确、有效。本文避开了风电机组的低电压穿越能力，这也是本文的后续工作，即计及风电场低穿特性的风电场等效模型。

［1］朱乾龙，韩平平，丁明，等.基于聚类-判别分析的风电场概率等值建模研究［J］.中国电机工程学报，2014，34（28）：4 770-4 780.

［2］王钤，潘险险，陈迎，等.基于实测数据的风电场风速-功率模型的研究［J］.电力系统保护与控制，2014，42（2）：23-27.

［3］周明，葛江北，李庚银.基于云模型的DFIG型风电场动态电压等值方法［J］.中国电机工程学报，2015，35（5）：1 097-1 105.

［4］李辉，王荷生，史旭阳，等.基于遗传算法的风电场等值模型的研究［J］.电力系统保护与控制，2011，39（11）：1-8，16.

［5］严干贵，李鸿博，穆钢，等.基于等效风速的风电场等值建模［J］.东北电力大学学报，2011，31（3）：13-19.

［6］余洋，刘永光，董胜元.基于运行数据的风电场等效建模方法比较［J］.电网与清洁能源，2009，25（12）：79-83.

［7］陈树勇，王聪，申洪，等.基于聚类算法的风电场动态等值［J］.中国电机工程学报，2012，32（4）：11-19，24.

［8］FREY B J，DUECK D.Clustering by Passing Messages Between Data Points［J］.Science，2007，315（5814）：972-976.