基于最小熵解卷积的谱峭度法在行星齿轮箱故障诊断中的应用
2018-03-14
(南昌航空大学 航空制造工程学院,南昌 330063)
0 引言
Wiggins[3]提出最小熵解卷积(MED)的处理方法能获得接近原始脉冲冲击信号。文献[4]将MED应用于提高自回归滤波器的脉冲残余信号检测齿轮裂纹。文献[5]利用MED结合谱峭度(SK)提升了滚动轴承中的故障检测及诊断能力。文献[6]使用最小熵反褶积(MED)与包络谱相结合能够检测到滚动轴承疲劳的影响。这些论文都表明,最小熵解卷积被成功的应用于横向振动信号的旋转机械故障诊断中,但没有将最小熵解卷积应用于行星齿轮扭转振动信号中。文献[7]通过行星齿轮箱扭转振动信号的幅值调制和频率调制对齿轮箱太阳轮故障扭转振动信号进行傅里叶频谱及包络谱分析得出了故障齿轮的幅值和频率调制特征,但此方法在诊断齿轮故障时不能直接提取低频故障齿轮特征频率及倍频成份。因此,基于上述的考虑本文提出一种基于最小熵解卷积的谱峭度方法,并应用于行星齿轮故障诊断中的故障行星齿轮扭转振动信号特征提取。该方法通过最小熵解卷积对行星齿轮箱扭转振动信号进行预处理,然后利用谱峭度能够发现信号中不稳定性的存在及能够指示哪个频率边带不稳定的优点,对预处理后的信号选择最优的频带和带通滤波参数进行带通滤波。将滤波后的信号通过希尔伯特变换进行包络解调,使低频故障信号从高频信号中解调出来。通过仿真信号和行星齿轮箱输出轴分别在承受10N.m、20N.m、30N.m载荷状态下采集到的行星齿轮故障扭转振动信号分析表明基于最小熵解卷积的谱峭度法能够很好的提取故障特征。
1 相关理论
1.1 最小熵解卷积理论
Wiggins[3]首先提出最小熵解卷积(MED)技术并且成功的应用于地震信号处理中。MED的基本原理是找到一种最优反向滤波器滤波参数使得输出信号的峭度值达到最大。因为峭度指标能够很好的反应故障冲击特性,如果信号中的峭度值得到提升,这将有助于行星齿轮箱的故障诊断。
图1阐明了MED方法的原理,冲击信号e(t)通过结构化滤波器得到的信号与噪声n(t)混合得到测量输出信号x(t),这是一个冲击信号与共振响应卷积的过程。x(t)通过反向滤波器f后得到y(t)尽可能接近原始冲击信号e(t)。
反向滤波器f的模型可以看作一个FIR滤波器L的系数并且可以写为:

式中,f(l)卷积系统FIR中的h,表达式如下:

延时lm是由反向滤波器造成的,它将移置整个信号,但不会改变脉冲间隔。
文献[8]指出反向滤波器f由MED中的目标函数法实现。对于最大化的峭度输出信号y(t),目标函数法是一个优化过程设计。目标函数法的实现是通过改变滤波器f的系数t。峭度被看作为归一化的四阶矩可以写为:

根据以f(l)为目标的导数为零,最大峭度可以获得:
原托辊支架由左支板、右支板和下底板组成,将水平托辊和垂直托辊[2]固定,并分别通过螺栓连接在电动铲运机后尾架边板上,如图1所示。在使用和维修过程中,存在如下问题:
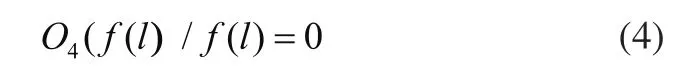
从上面的理论可以看出MED可以抑制原始信号的噪声干扰,使得输出冲击信号的峭度值达到最大。
1.2 谱峭度
文献[9]首次提出谱峭度(SK)并应用于声纳探测信号中。Antoni[10]首次将SK应用于轴承故障诊断中。这种基本方法是计算每一个频率线的峭度,从而发现隐藏的不稳定性的存在及指示哪一个频率边带不稳定。文献[10]正式的定义了非平稳信号的谱峭度,将任何零均值非平稳y(t)称为随机过程,给出了信号y(t)的表达式如下:

式中dZy(f)是一个标准正交的频谱增量,H(t,f)是y(t)在频率f处的复合包络。信号y(t)的谱峭度定义为四阶频谱积累,用如下公式表示:

式中Ky(f)为信号y(t)的谱峭度。
Antoni[11,12]提出两种方法计算谱峭度。第一种方法称为STFT寻找最优滤波器峭度图。第二种方法称为快速谱峭度法。文献[13]提升了谱峭度计算速度,提出快速谱峭度的计算方法。文献[14]指出谱峭度在信噪比较高的情况下对瞬态冲击信号的识别效果更好。因此本文将快速谱峭度应用于MED预处理后的信号进行寻找最优带通滤波参数。
2 诊断算法流程
第一步是MED预处理。通过MED对扭转振动信号进行预处理,降低信号中的噪声,使输出冲击信号的峭度值得到提升。
第二步是带通滤波。通过快速谱峭度图得出最优带通滤波参数,然后进行带通数字滤波。
第三步是包络解调。通过Hilbert变换对滤波后的信号进行包络解调,将信号中的低频特征信息从高频信号中解调出来。
第四步是得到包络谱。通过对低频信号进行傅利叶变换,得到包络谱。从低频信号包络谱中看故障特征频率及周期性故障冲击特性来判断齿轮的状态。
诊断流程如图2所示。
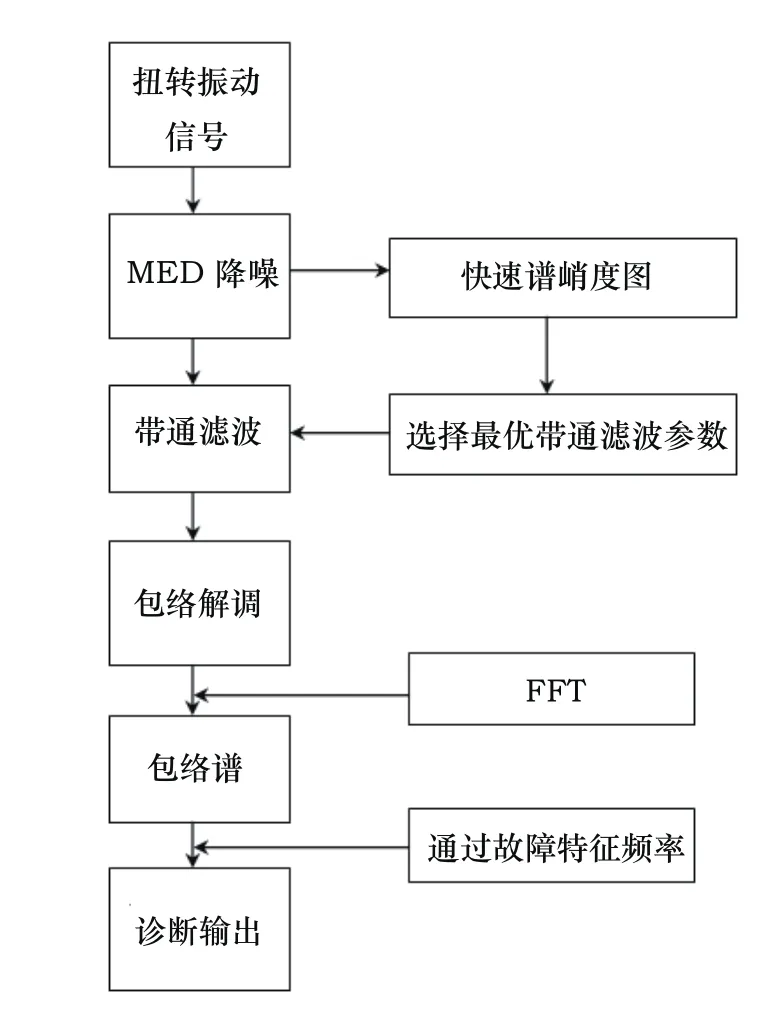
图2 行星齿轮故障诊断流程
3 试验设备及数据获取
试验设备为上海磊诺传动设备有限公司生产的PXDS115-4型单级行星齿轮箱,行星齿轮的基本参数如表1所示。行星齿轮箱相应的旋转频率及故障特征频率如表2所示。齿轮箱驱动电机参数由额定转速为1430r/min、额定功率为3.0kW的三相异步交流电动机驱动。试验平台的布置如图3所示,实验平台图解视图如图4所示。通过对实验平台中磁粉制动器激励电流大小的控制,可以使得行星齿轮箱承受不同扭矩大小的负荷。利用Labview虚拟仪器进行数据采集时,采样频率定为10000Hz,每个文件采集167583个点。通过对磁粉制动器激励电流大小的调节,分别采集故障行星齿轮在齿轮箱输出轴承受10N.m、20N.m、30N.m扭矩大小的扭转振动信号。行星齿轮箱行星轮中的3个行星齿轮及故障行星齿轮2如图5所示。

图3 实验平台

图4 实验平台图解视图

图5 故障行星齿轮2

表1 行星齿轮基本参数
4 仿真信号分析
仿真信号由噪声、谐波信号及脉冲信号三种信号复合而成。其表达式可写为如下:


表2 行星齿轮箱相应的旋转频率及故障特征频率

图6 仿真信号的时域图及频域图

图7 MED预处理后的信号时域图
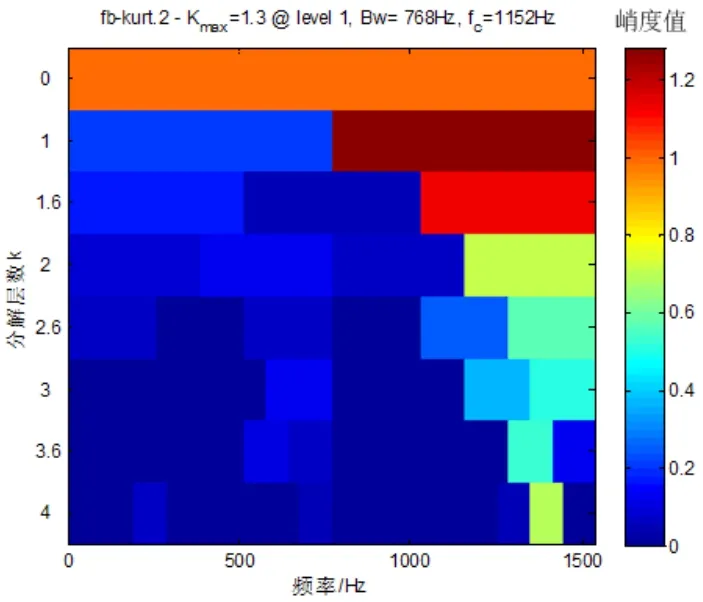
图8 MED预处理后的谱峭度图

图9 信号MED-SK方法和原始信号的包络谱
5 实际信号分析
1)对采集到的行星齿轮箱在输入轴的转速为1430r/min,输出轴承受10N.m扭矩的故障行星齿轮扭转振动信号进行分析。信号的时域图如图10(a)所示,频域波形如图10(b)所示。从原始信号频域图10(b)中看出行星齿轮故障特征频率17.87Hz被噪声淹没。MED预处理后的信号谱峭度如图11所示。从谱峭度图11中可以看出最大峭度处的峭度值为3.9,中心频率为1250Hz,带宽为2500Hz。进行带通滤波后,再使用包络谱分析得到包络谱如图12(a)所示。原始信号的包络谱如图12(b)所示。从图12(a)可以看出MED-SK方法的包络谱可以准确的识别接近行星齿轮故障特征频率17.87Hz的行星齿轮故障特征频率17.73Hz及以17.73Hz为周期的故障冲击倍频成份。而原始信号图12(b)的包络谱中只能看出行星齿轮故障频率及频率调制现象,但相应的以17.73Hz为频率间隔的故障冲击特性不易轻易看出。
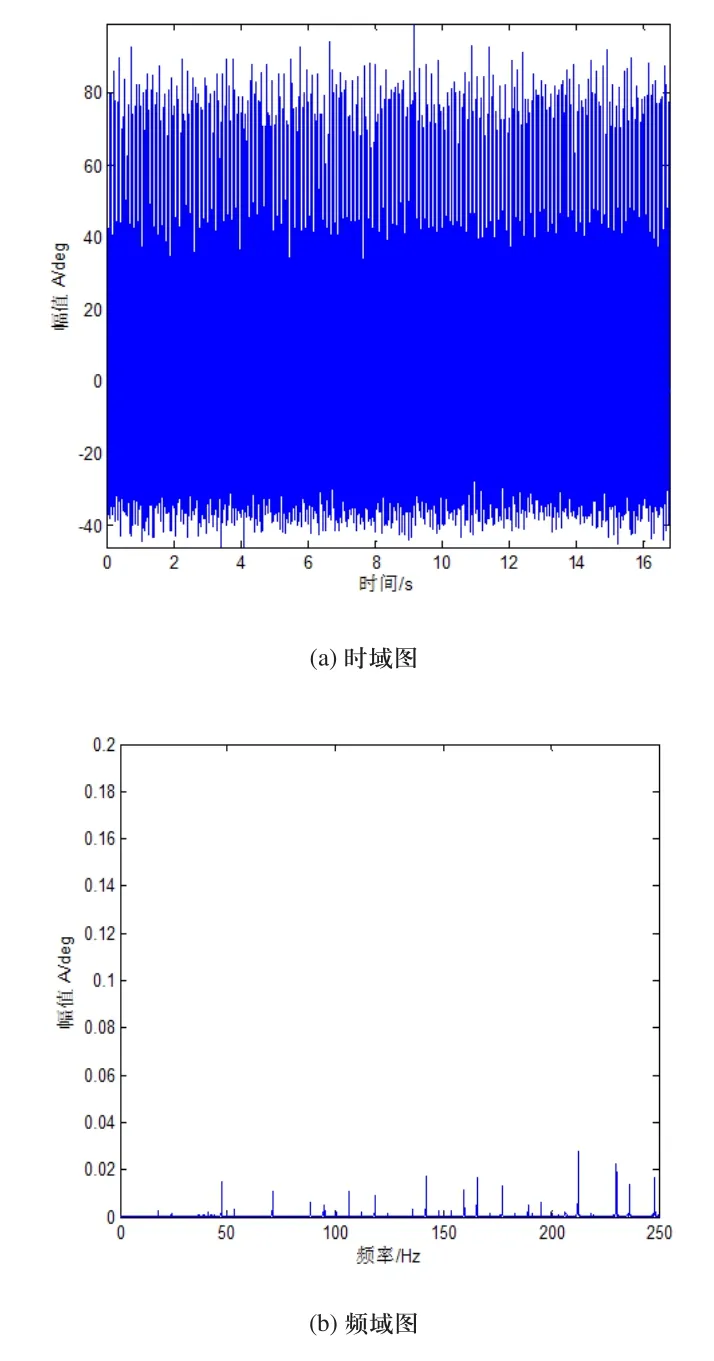
图10 输出轴承受10N.m时的时域图和频域图
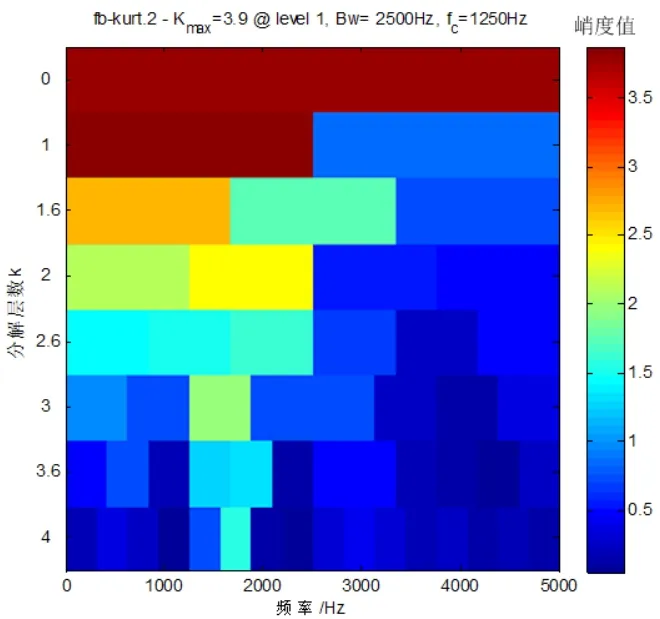
图11 MED预处理后的谱峭度图
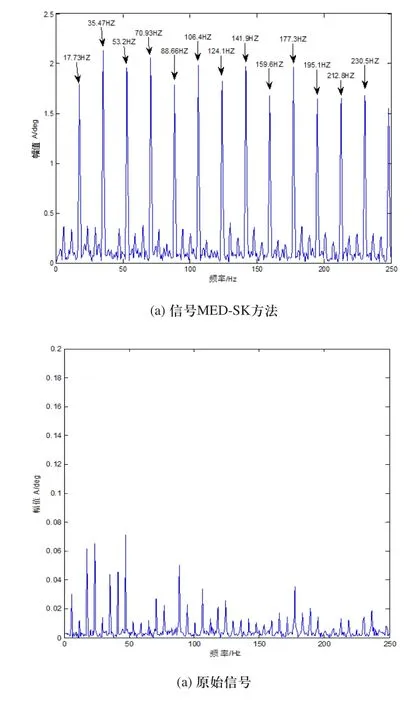
图12 信号MED-SK方法和原始信号的包络谱
2)对采集到的行星齿轮箱在输入轴的转速为1430r/min,输出轴承受20N.m扭矩的故障行星齿轮扭转振动信号进行分析。信号的时域图如图13(a)所示,频域波形如图13(b)所示。从原始信号频域图13(b)中看出行星齿轮故障特征频率17.87Hz不能被识别出来。MED预处理后的信号谱峭度如图14所示。从谱峭度图14中可以看出最大峭度处的峭度值为8.4,中心频率为1250Hz,带宽为2500Hz。进行带通滤波后,再使用包络谱分析得到包络谱如图15(a)所示。原始信号的包络谱如图15(b)所示。从图15(a)可以看出MED-SK方法的包络谱可以准确的识别接近行星齿轮故障特征频率17.87Hz的故障特征频率17.59Hz及以17.59Hz为周期的故障冲击倍频成份。而原始信号图15(b)的包络谱中只能看出故障频率及频率调制现象,但相应的以17.59Hz为频率间隔的故障冲击特性不易轻易看出,相比输出轴承受10N.m扭矩的故障行星齿轮原始信号包络谱可以看出输出轴在承受20N.m扭矩时的故障冲击特性更加明显。


图13 输出轴承受20N.m时的时域图和频域图
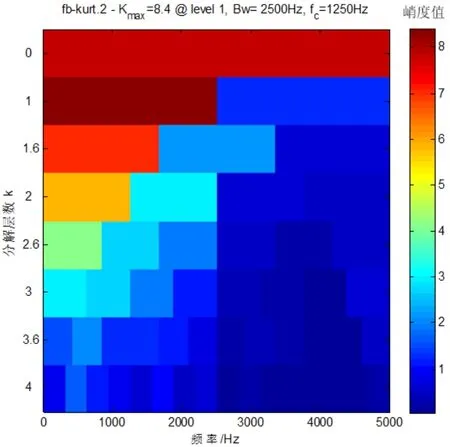
图14 MED预处理后的谱峭度图
3)对采集到的行星齿轮箱在输入轴的转速为1430r/min,输出轴承受30N.m扭矩的故障行星齿轮扭转振动信号进行分析。信号的时域图如图16(a)所示,频域波形如图16(b)所示。从原始信号频域图16(b)中看出行星齿轮故障特征频率17.87Hz不能被识别出来。MED预处理后的信号谱峭度如图17所示。从谱峭度图17中可以看出最大峭度处的峭度值为16.8,中心频率为2500Hz,带宽为5000Hz。进行带通滤波后,再使用包络谱分析得到包络谱如图18(a)所示。原始信号的包络谱如图18(b)所示。从图18(a)可以看出MED-SK方法的包络谱可以准确的识别接近行星齿轮故障特征频率17.87Hz的故障特征频率17.43Hz及以17.43Hz为周期的故障冲击倍频成份。而原始信号图18(b)的包络谱中只能看出故障频率及频率调制现象,但相应的以17.43Hz为频率间隔的故障冲击特性不易轻易看出,相比输出轴承受10N.m和20N.m扭矩的故障行星齿轮原始信号包络谱可以看出输出轴在承受30N.m扭矩时的故障冲击特性更加明显。
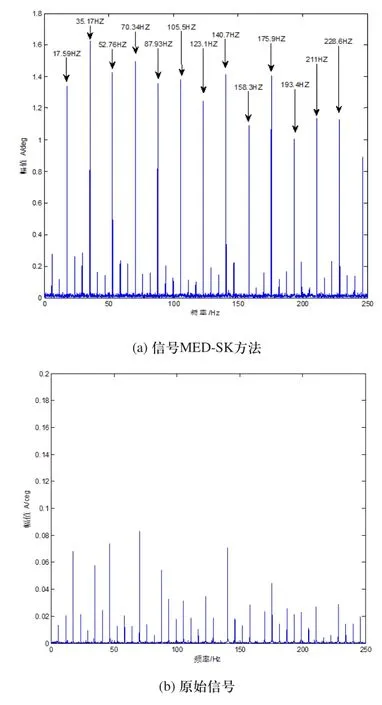
图15 信号MED-SK方法和原始信号的包络谱

图16 输出轴承受30N.m时的时域图和频域图

图17 MED预处理后的谱峭度图
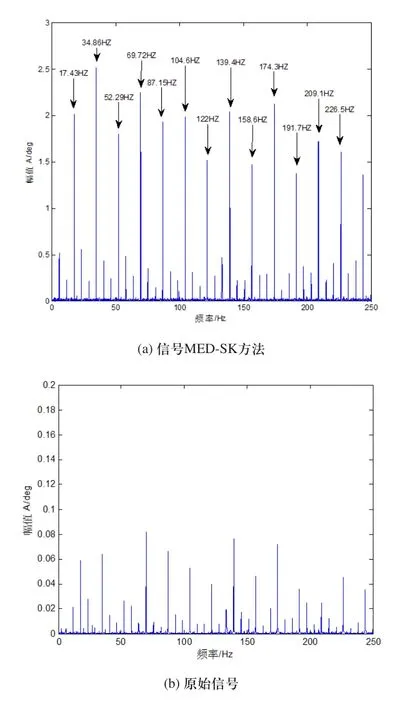
图18 信号MED-SK方法和原始信号的包络谱
6 结论
针对噪声干扰状态下行星齿轮箱故障诊断中的齿轮故障特征提取,从仿真信号和输出轴承受多种载荷状态下的实际行星齿轮箱行星齿轮故障扭转振动信号分析表明:通过最小熵解卷积对信号进行降噪预处理后,再对处理后的信号利用谱峭度图选择合理的带通滤波参数进行带通滤波后,最终得到MED-SK方法的包络谱能够准确的提取仿真信号中的脉冲频率冲击特征以及行星齿轮箱在承受多种载荷状态下的实际故障行星齿轮扭转振动信号中的故障冲击频率特征。与原始信号的包络谱进行比较可以看出,原始信号的包络谱除故障冲击频率成分被识别外,其他齿轮旋转频率对故障齿轮特征频率的调制现象也比较明显,没有重点突出故障冲击周期性特征。而本文提出的MED-SK方法的包络谱用于行星齿轮故障特征提取时能够重点突出行星齿轮故障特征频率及故障倍频周期性冲击成分。
[1]L.D. Jiang,S.Chang,G.H. Dai, Z.R.Zhu,Fault diagnosis and analysis for marine planetary gearbox[J].Key Engineering Materials.2010,419-420:149-152.
[2]F. Chaari, T. Fakhfakh, M. Haddar, Dynamic analysis of a planetary gear failure caused by tooth pitting and cracking[J].Journal of Failure Analysis and Prevention.2006,6:73-78.
[3]Ralph A Wiggins, Minimum entropy deconvolution[J].Geoexploration.1978,16:21-35.
[4]H. Endo, R. Randall, Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J].Mechanical Systems and Signal Processing.2007,21:906-919.
[5]N. Sawalhi, R. Randall, H. Endo, The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis[J].Mechanical Systems and Signal Processing.2007,21:2616-2633.
[6]R. Jiang, J.Chen,G.Dong, T. Liu, W. Xiao, The weak fault diagnosis and condition monitoring of rolling element bearing using minimum entropy deconvolution and envelope spectrum[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science.2013,227(5):1116-1129.
[7]冯志鹏,褚福磊.行星齿轮箱故障诊断的扭转振动信号分析方法[J].中国电机工程学报,2013,33(14):101-106.
[8]J.-Y. Lee, A. Nandi, Extraction of impacting signals using blind deconvolution[J].Journal of Sound and Vibration.2000,232:945-962.
[9]R. Dwyer, Detection of non-Gaussian signals by frequency domain kurtosis estimation[A].Acoustics,Speech,and Signal Processing,IEEE International Conference On ICASSP,Boston[C],1983,8:607-610.
[10]J. Antoni. The spectral kurtosis: a useful tool for characterising non-stationary signals[J].Mechanical Systems and Signal Processing.2006,20:282-307.
[11]J. Antoni, R.B. Randall, The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines[J],Mechanical Systems and Signal Processing. 2006, 20:308-331.
[12]J. Antoni, Fast computation of the kurtogram for the detection of transient faults[J].Mechanical Systems and Signal Processing.2007,21:108-124.
[13]McDonald G L,Zhan Qing, Zuo M J.Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection[J],Mechanical Systems and Signal Processing.2012,33:237-255.
[14]石林锁,张亚洲,米文鹏.基于WVD的谱峭度法在轴承故障诊断中的应用[J].振动、测试与诊断,2011,31(1):27-31.
