带中心孔的阶梯-圆锥型超声变幅杆优化设计

（泰州职业技术学院，泰州 225300）

0 引言

近年来，一些新型的硬脆材料如C/SiC、光学玻璃、蓝宝石、人造水晶、高温合金等在航空航天、汽车、能源等领域得到了越来越多的应用，而这些硬脆材料却不如传统材料容易加工，而采用传统机械加工方法时容易出现纤维丝裂、微裂纹、毛刺等缺陷，且道具磨损严重哦国内，效率低。超声振动加工技术被认为是最适合加工硬脆材料的加工方法之一，将在原有机械加工的刀具上施加超声振动，与传统加工相比，具有加工作用力小、加工温度低、排泄效果好、加工质量与加工效率高等优点[1～7]。

目前，国内外对变幅杆的设计，主要设计方法有解析法、机电等效法、表面弹观法、有限元法。其中有限元法是目前应用较广泛的数值分析技术之一，其求解基本思想是将问题的求解区域划分为一系列单元，各单元之间通过节点连接，由平衡关系或者能量关系建立节点间的方程组，通过边界条件即可求解，该方法能满足工程设计要求[8～14]。

本文设计一种高速旋转超声振动主轴，而变幅杆作为振动系统的一个重要部件，其结构直接影响高速旋转超声主轴的结构。本文基于超声理论，解析法和有限元法相结合，设计1/4波长，频率为20kHz，带中心孔的复合型变幅杆。首先进行变幅杆各部分尺寸理论计算，然后在此基础上进行有限元分析和优化设计，理论计算与优化设计相结合，指导变幅杆的制造，减少设计周期和设计成本。

1 纵向振动的波动方程

图1为一变截面杆，其对称轴为坐标轴x，作用在小体积元（x，x+dx）所限定的区间上的张应力为在对模型做必要的简化后，根据牛顿定律可以写出动力学方程[15]。

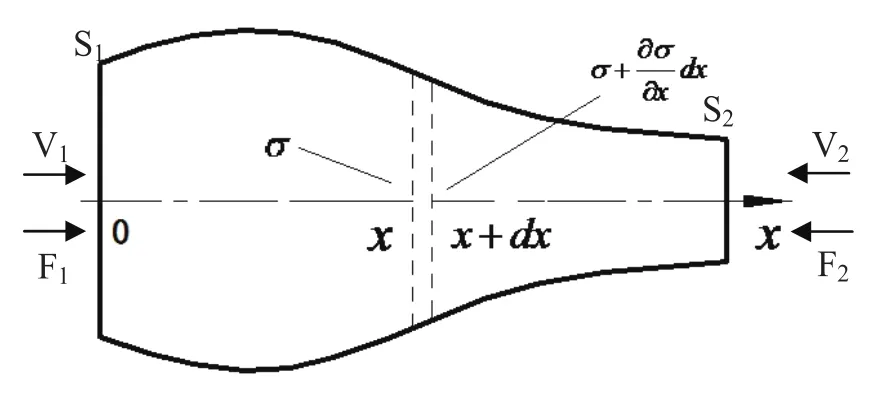
图1 变截面棒的纵振示意图

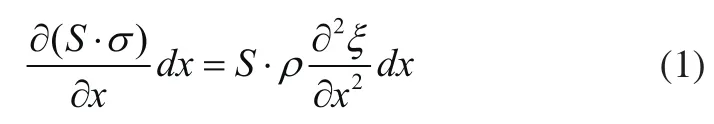
在简谐振动情况下，式(1)可以写为：

对等截面杆：

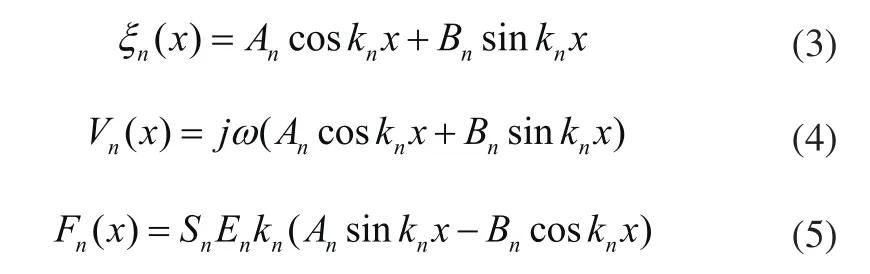
对圆锥形截面杆：

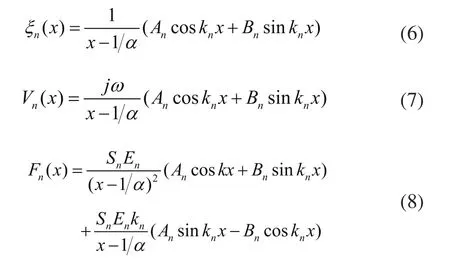
式中，An，Bn分别为待定常数，α为锥度系数，D2分别为圆锥变幅杆大端、小端的直径，l为其长度。

2 变幅杆的理论计算

常用的变幅杆有圆锥形、阶梯型、指数型等，其中，阶梯形变幅杆获得的放大系数较大，但存在应力集中的不足，圆锥形变幅杆的放大系数较小，但是其共振频率和放大系数受负载的影响相对较小，因而结合上述两种变幅杆的特点，设计圆锥阶梯复合形变幅杆。为提高变幅杆回转精度，减小体积，并便于加工制作和安装，设计图2所示的1/4波长复合型变幅杆，波长按λ=c/f计算，径向直径小于该波长的四分之一，并将变幅杆的节面位置在x=0处。

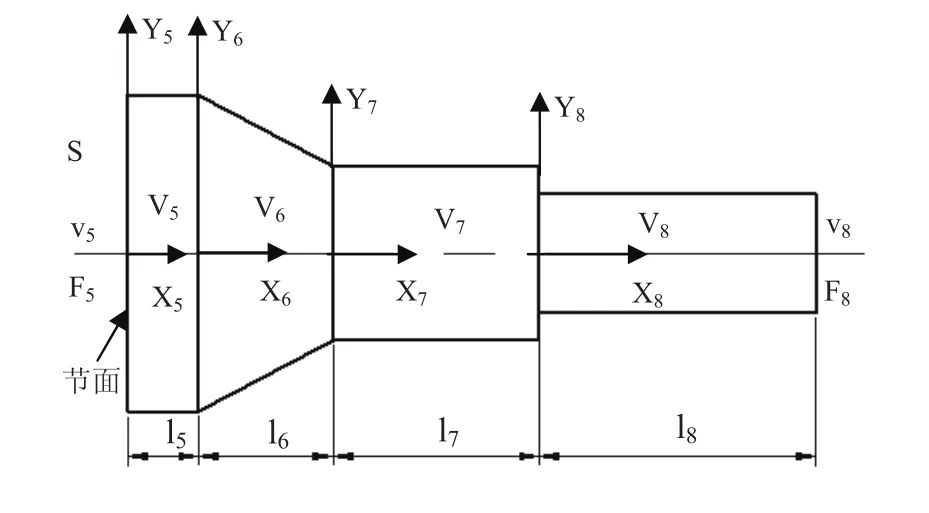
图2 变幅杆结构示意图

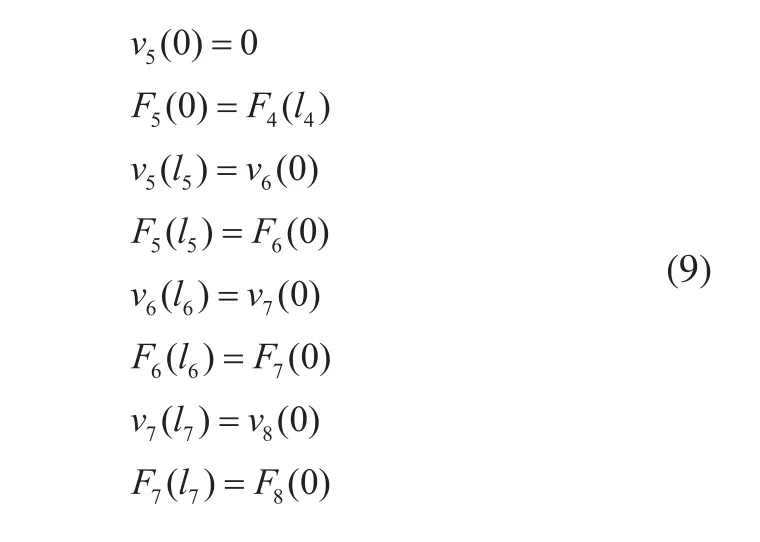
为了计算简便，分别对每个元件建立坐标系，在不考虑工具的影响下，变幅杆一端固定，一端自由，由等截面杆及圆锥界面杆的波动方程式(4)、式(5)、式(7)、式(8)以及函数在临界面处的连续性，可以得到方程组式(9)。

解方程组(9)可以得到关于l5、l6、l7和l8的等式，其中l6，l7，l8是要进行设计的值。所设计的是1/4波长变幅杆，l6，l7，l8的取值范围不能超过1/8波长。基于l6，l7的值便可求出相对应的l8的值，利用MATLAB进行求解[16]，结果如表1所示。

从表中数据分析可知，随着l6的增长，l8逐渐减小，而随着l7的增长，l8也是逐渐减小的，在两者变化当中，l7的增长对l8的减小比较明显，这为后续变幅杆有限元分析和优化设计的有限元模型的建立提供基础，并且在后续的变幅杆制作过程中，有关频率的调整、尺寸的调整提供指导。

3 超声变幅杆的有限元分析

在得到变幅杆的理论尺寸范围的前提下，可以直接对变幅杆进行优化设计，其有限元分析过程包括模态分析、谐响应分析与优化设计[17,18]。

3.1 超声变幅杆的模态分析

为了减小尺寸过大，质量过重给整个超声振动系统带来的不便，超声变幅杆尺寸尽可能的小。从表1中任意选取一组变幅杆的数据来进行分析，而在实际中，考虑到变幅杆将通过ER11螺母来连接工具，因此将仿真的几何模型尽可能逼近实际变幅杆模型，首先选取l6=16mm，l7=26mm，l8=28mm，为了方便变幅杆冷却，内部设置Ф5㎜通液流道，如图3所示，这里，l8=l'8+l9，而l5作为一个法兰盘厚度，取5mm。对变幅杆进行模态分析，得到变幅杆的纵向振动的频率以及位移分布，如图4所示。需要说明的问题是，在位移分布中，仅仅表征了位移沿纵向的分布情况。此时频率为21227Hz，接近所设计的频率2000Hz，可以作为优化目标进行后续分析，提取该频率，并设为F，为后续的变幅杆优化设计提供参数。

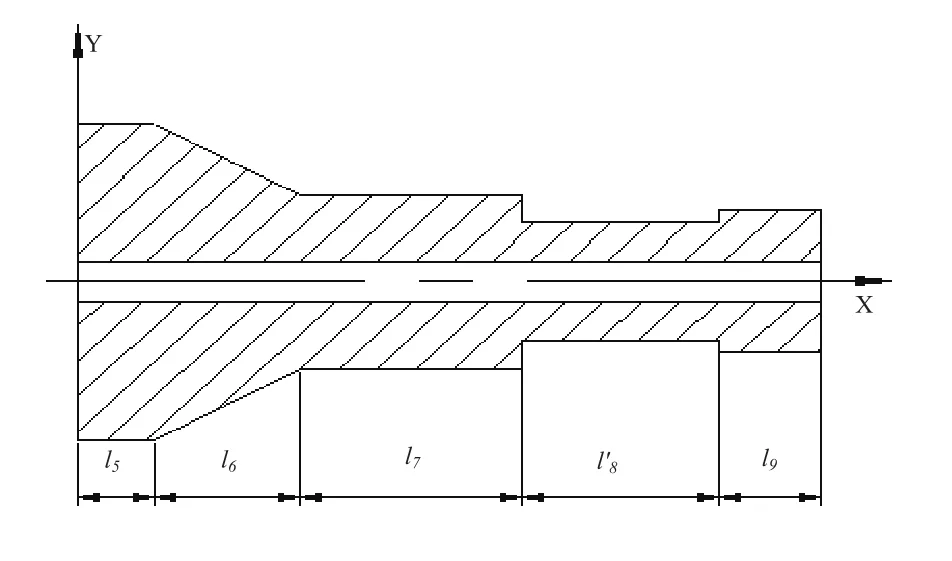
图3 变幅杆示意图

3.2 超声变幅杆的谐响应分析

变幅杆的谐响应分析的主要是针对变幅杆的固有频率在外加频率下的振幅和受力情况。在模态分析结果中，所得到的纵向振动频率为21227Hz，设置搜索频率区间为19227Hz～22227Hz，迭代步为10，变幅杆大端加载振幅为5μm的输入响应，得到变幅杆在有激励输入的情况下末端的振幅大小以及变幅杆的应力分布情况，如图5、图6所示。

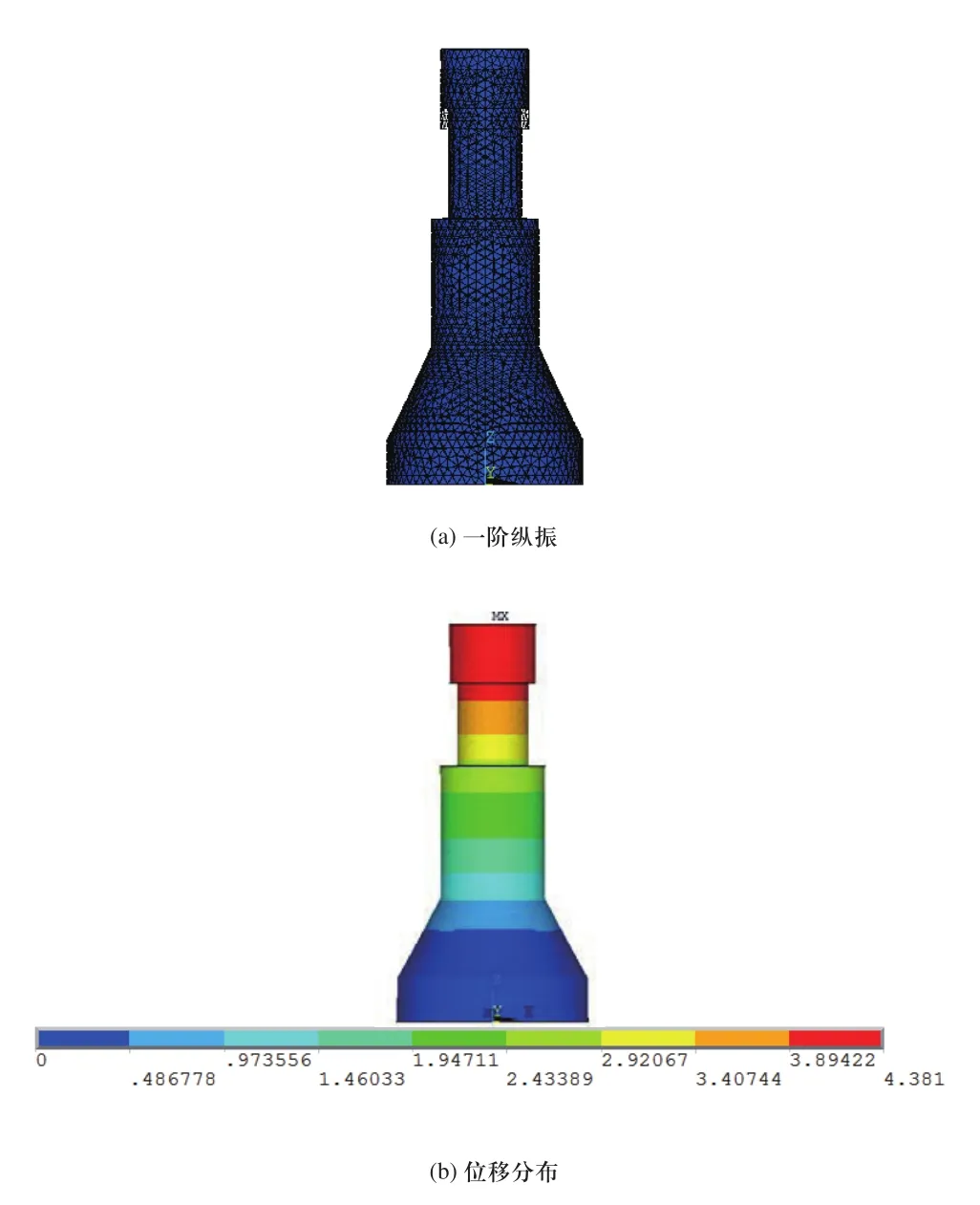
图4 超声变幅杆一阶纵向振动f=21227Hz

谐响应分析结果中，频率为19827Hz最靠近设计频率，更容易发生共振，故查看该频率下的振幅及应力分布云图，从图中可以看出，变幅杆小端处的振幅最大，为59μm，变幅杆截面突变处最大应力为286MPa。选取最大应力为参数Str_max，为后续的变幅杆优化设计提供参数。

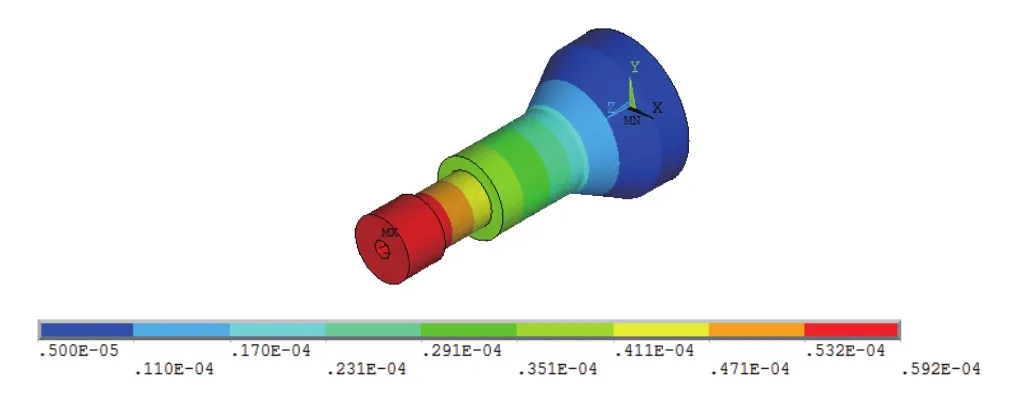
图5 19827Hz振幅分布云图

图6 19827Hz应力分布云图

3.3 超声变幅杆的优化设计

对所建立的模型分别进行模态分析和谐响应分析后，提取应力函数STRESS_MAX作为优化的状态变量（SV），以l6、l7和l8为设计变量（DV），而目标函数为频率函数，作为最优值，其评价指标是越接近20000Hz为最佳，因此，以设计频率与模态分析频率F之差的绝对值FREQ为目标函数（OBJ），进行优化设计，其优化结果如表2所示。

最后对优化所得到的长度进行圆整，并进行模态和谐响应分析，其仿真结果频率为19913Hz，该变幅杆轴向位移分布如图7所示，沿变幅杆轴向长度变化，振幅逐渐变大，输出端的位移为75μm。

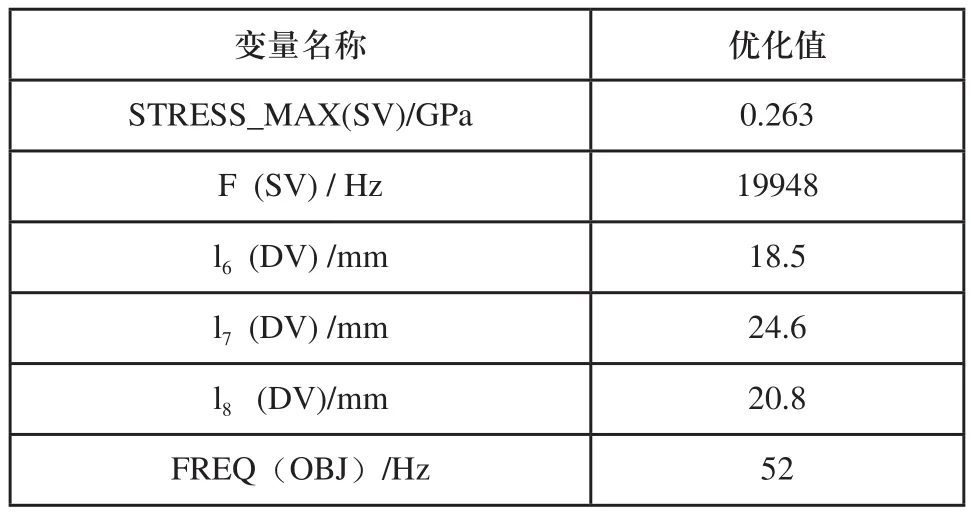
表2 变幅杆优化结果

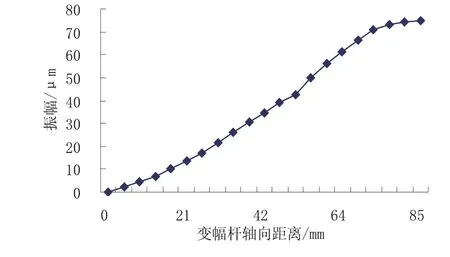
图7 变幅杆轴向位移分布图

最后根据理论计算结果的复合型变幅杆的各尺寸的分布情况以及变幅杆优化设计的结果进行了变幅杆的制作与调试，结果表明，通过优化设计能够快速的设计出变幅杆的基本模型，但该基本模型不一定能满足设计要求，因此，结合理论计算结果，调整变幅杆的各尺寸的大小，能快速的制作出满足设计要求的变幅杆，最后设计的变幅杆如图8所示。

图8 超声变幅杆实物图

4 结论

本文进行了高速旋转超声主轴中振动系统中变幅杆的开发。基于超声理论和有限元理论，优化设计了频率为20kHz，1/4波长复合型变幅杆。首先基于波动方程，进行了变幅杆的理论计算，得到了1/4波长变幅杆的最初几何模型的范围以及各尺寸的分布情况，在此基础上，利用有限元软件ANSYS对1/4波长变幅杆进行了模态分析，谐响应分析，最后基于以上的分析进行了优化设计，得到了变幅杆优化结果。但由于仿真所设置的参数与实际材料的参数具有一定的偏差以及ANSYS软件本身存在的误差，其仿真结果也会与实体频率有一定偏差，因而将理论分析与有限元分析之结果综合起来用于指导变幅杆的设计与制作，结果表明，这样能够减少变幅杆的设计与制作的时间和成本。

[1]郭景哲,贾宝贤,王冬生,等.微细深孔加工研究进展及关键技术分析[J].机械设计与制造,2009(10):257-258.

[2]高霁,曹国强.特种加工微小孔技术及其发展现状[J].机械设计与制造,2005(7):169-171.

【】【】

[3]郑书友,冯平法,吴志军,等.超声加工技术的发展及其在航空航天制造中的应用潜能[J].航空制造技术,2009(13):51-54.

[4]Ranko Tsuboi, Yasuhiro Kakinuma, Tojiro Aoyam，et al．Ultrasonic Vibration and Cavitation-aided Micromachining of Hard and Brittle Materials[J].Procedia CIRP 1(2012):342-346.

[5]高飞.微细旋转超声加工机理及相关技术研究[D].上海:上海交通大学,2013,2.

[6]W.L. Cong，Z.J. Pei,T.W. Deines,et al.Rotary ultrasonic machining of CFRP composites：A study on power consumption[J].Ultrasonics 52(2012):1030-1037.

[7]W.L. Cong,Z.J. Pei,X. Sun,et al.Rotary ultrasonic machining of CFRP:A mechanistic predictive model for cutting force[J].Ultrasonics 54(2014):663-675.

[8]温平方,顾晓波,吴晓峰.圆锥过渡段阶梯形复合变幅杆的模态分析及优化设计[J].现代制造工程,2008(11):111-113.

[9]李彬,李亚,孟鑫,等.超声变幅杆参数化优化设计研究[J].机械设计与制造,2013(11):60-63.

[10]王慧敏,鲍善惠,江长青.粗细端截面比对阶梯变幅杆谐振频率的影响[J].声学技术,2004,23(4):242-245.

[11]高洁.复合多段式变幅杆优化设计及声学特性分析[J].陕西师范大学学报,2006,34(4):44-46.

[12]刘战峰,李培繁,王天琦.超声复合变幅杆的设计与研究[J].现代制造工程,2008(2):102-105.

[13]张向慧.旋转超声加工振动系统设计及关键技术研究[D].北京:北京林业大学,2011.

[14]张云电.超声加工及其应用[M].北京:国防工业出版社,1995.

[15]林仲茂.超声变幅杆的原理和设计[M].北京:科学出版社,1987.

[16]陈杰.MATLAB宝典[M].北京:电子工业出版社,2007.

[17]张红松,胡仁喜,康士延,等.ANSYS12.0有限元分析入门到精通[M].北京:机械工业出版社,2010.

[18]莫喜平.ANSYS软件在模拟分析声学换能器中的应用[J].声学技术,2007,26(6):1279-1290.