阿白冲水库大坝静应力及变形计算分析
2018-03-13
(云南省红河州水利水电勘察设计研究院,云南 蒙自 661100)
1 工程概况
阿白冲水库地处石屏县红河二级支流阿白冲河中下游河段,是以农业灌溉为主的中型水利枢纽,水库总库容1538.0万m3,灌溉面积1940hm2,年供水总量1718.8万m3。工程等别为Ⅲ等,大坝为黏土心墙坝,坝顶高程1567.00m,坝顶长256.5m、宽10.0m,最大坝高89.4m。上游坝坡自上而下为1∶2.5、1∶2.75、1∶3.0。下游坝坡自上而下为:1∶2.0、1∶2.25、1∶2.75、1∶1.5,变坡处均设置宽2.5m的戗台。黏土防渗心墙顶部高程1566.00m,顶宽4m,上、下游边坡均为1∶0.2,底部高程1477.60m,心墙最大高度88.4m,最大底宽39.36m。坝体剖面如图1所示。
2 坝体静应力及变形计算
采用三维非线性有限元进行坝体应力及变形计算,采用比奥固结理论进行心墙及反滤料的有效应力应变分析,用总应力法进行上、下游坝壳的应力及应变分析。静力计算分析采用“南水”双屈服面弹塑性模型。
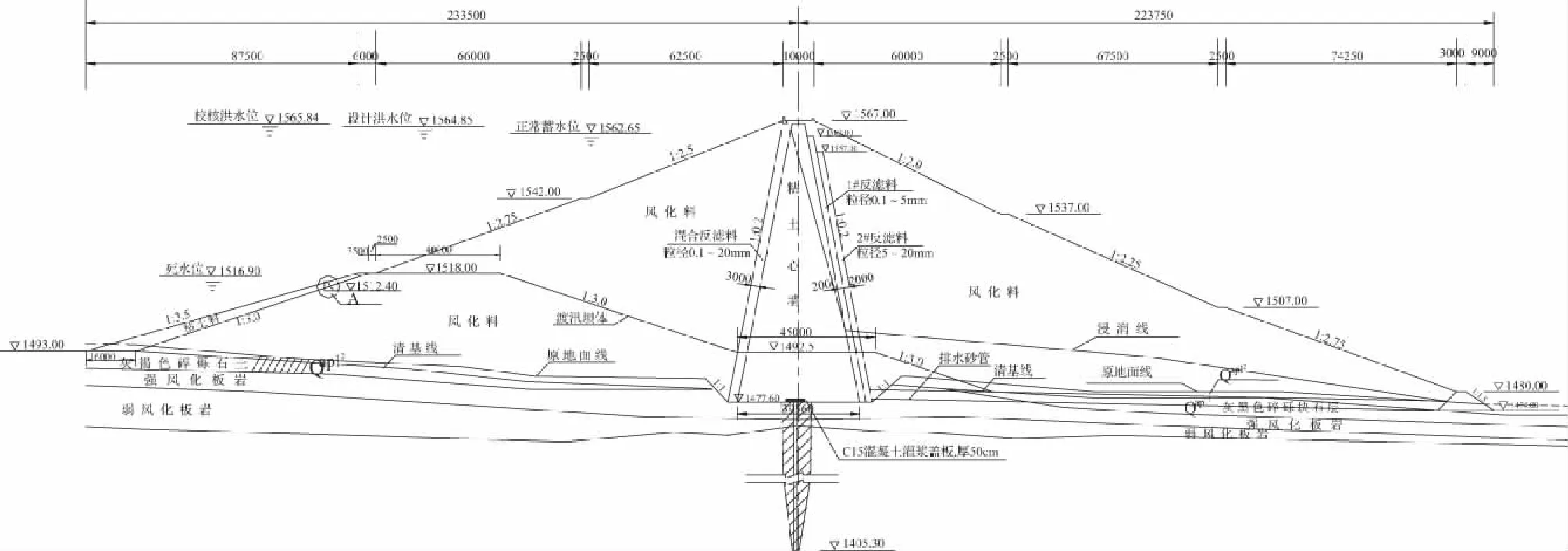
图1 坝体标准横剖面
2.1 Biot固结理论
三维问题的Biot固结方程表达式为:
(1)
(2)
(3)
(4)
式中,wx、wy、wz分别为三个方向的位移;u为孔隙水压力;G、ν分别为剪切模量和泊松比,且G=E/2(1+ν),E为杨氏模量;2为拉普拉斯算子。公式(1)、(2)、(3)为平衡方程,(4)为连续方程。由式(4)可知,孔隙水压力和变形密切相关,而且随时间变化。采用有限元对计算区域进行离散,并将时间划分成多个时段,对该组公式进行推导可得有限元计算的支配方程。
2.2 风化料及黏土料骨架静力本构模型
心墙土体及坝壳风化料的应力应变关系均采用“南水”模型模拟。增量型的应力应变关系为:
Δσ=[D]epΔε
(5)
其弹塑性模量矩阵:
[D]ep=[dij] (i,j=1~6)
(6)
双屈服面弹塑性模型由下列双屈服面组成:
(7)

模型的基本变量为切线杨氏模量Et和切线体积比μt,分别由式(8)、(9)求出:
(8)
式中,pa为标准大气压力值,Ei为初始切线模量。
(9)
式中,Rs=RfSl,而Sl为应力水平,有:
(10)
(σ1-σ3)f由莫尔—库伦(Mohr-Coulomb)准则确定:
(11)
式中,c、φ分别为有效应力强度指标的凝聚力和摩擦角。
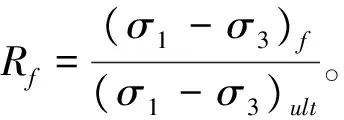
卸荷情况下,回弹模量按下式计算:
Eur=KurPa(σ3/Pa)n
(12)
9个计算参数K、Kur、n、c、φ、Rf、cd、nd和Rd,由三轴固结排水剪试验得出。南水双屈服面弹塑性模型亦可采用Duncan E-ν模型的参数进行计算,此时切线体积比μt按下式计算:
μt=1-2νt
(13)
式中,νt即为Duncan E-ν模型中的切线泊松比,表达式为:
(14)
对比式(9)和(14),采用Duncan E-ν模型的参数G、D、F来代替双屈服面弹塑性模型的参数cd、nd、Rd,仍然可以采用双屈服面弹塑性模型进行计算分析。
关于加卸荷准则,设
a.F1>(F1)max
b.F2>(F2)max
若a、b同时成立表示全加荷;若a、b同时不成立表示全卸荷;若其中之一成立、其中之一不成立则表示部分加荷。
风化料等粗颗粒材料的强度包线通常为非线性,按Duncan-zhang模型,取凝聚力c=0,内摩擦角φ按下式计算。
φ=φ1-Δφ·lg(σ3/Pa)
(15)
式中,φ1为σ3等于1个大气压时的φ角,Δφ是σ3增加10倍大气压时φ角的减少量。
2.3 心墙土孔隙流体模型
在对心墙土料进行基于Biot固结理论的有效应力变形分析中,土体中孔隙流体的流动假定服从Darcy定律,其压缩按如下模式考虑:假定孔隙气以气泡形式封闭或溶解于孔隙水中,把水气混合体当作可压缩的流体对待,其压缩系数cp按下式考虑:
(16)
其中ns为初始孔隙率,Sr为饱和度,co为无气水压缩系数,其值为4.7×10-6m2/t,Pw为孔隙水压力。
假定填筑时的初始饱和度为Sro,坝体填筑过程中随着上覆荷重的增大,土体所受孔隙压力逐步加大,孔隙气逐步溶解于水中,饱和度逐步增加,其变化规律如下:
(17)
其中Ch为Henry溶解系数,取值0.02。
2.4 计算参数
坝料静应力及变形模型计算参数根据室内试验成果及地质勘察报告,结合工程类比法确定,静力计算(南水模型)参数如表1所列。
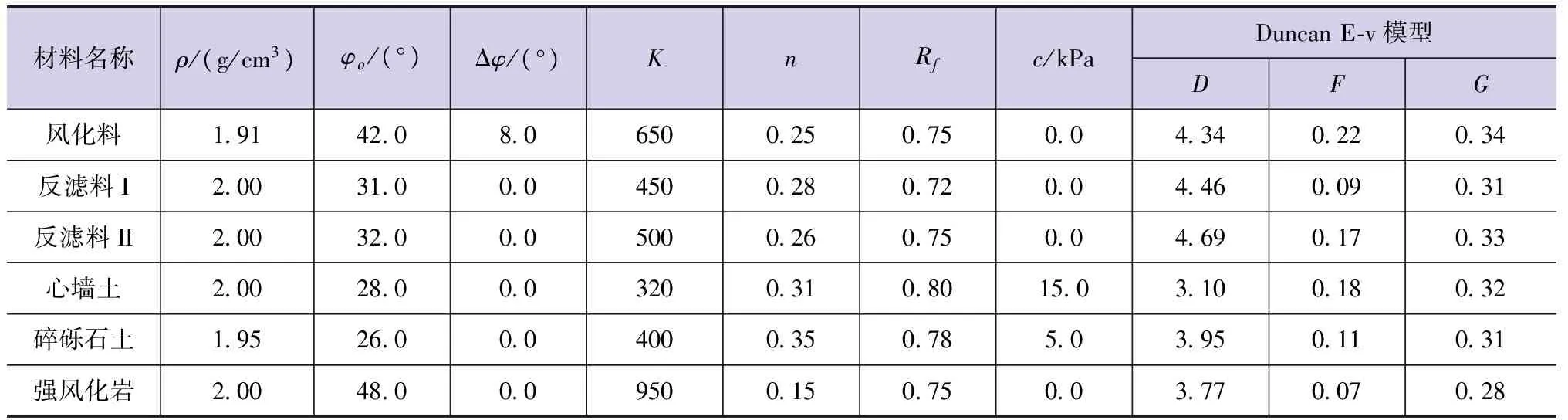
表1 计算参数
2.5 计算静力荷载
静力荷载包括坝体自重和蓄水期的水荷载。坝体自重通过模拟坝体施工填筑过程逐级施加,水荷载则通过模拟水库蓄水过程逐级施加。
2.6 网格剖分及模拟分级
2.6.1 施工顺序
静力计算全面模拟了坝体的施工填筑及水库的蓄水过程。该工程总施工期50个月,其中:第一年12月初—第二年11月底进行河床开挖;第二年12月初—第三年6月底进行度汛坝体填筑;第三年10月初—第五年11月底进行排水体、坝体及坝面工程施工。
2.6.2 三维网格
采用三维有限元网格剖分模拟坝体分级填筑过程,三维网格如图2所示。
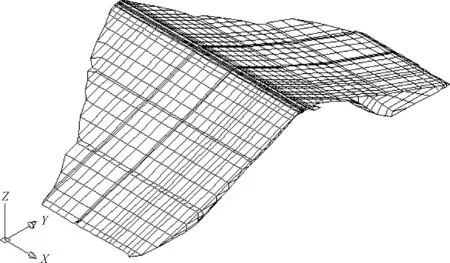
图2 三维网格
2.6.3 分级模拟
有限元模拟计算顺序为:坝基开挖→度汛坝体填筑→坝脚排水体、坝体及坝面工程施工→水库蓄水。模拟计算分45级进行,第1级模拟浇筑混凝土底板,第2~6级模拟度汛坝体填筑,第7级模拟停工3个月,第8级模拟排水体施工,第9~25级模拟坝体填筑至坝顶1567.00m,第26~30级模拟库水蓄至正常水位1562.62m,第31~45级模拟水库蓄水运行5年。
2.7 坝体静力应力及变形计算结果
2.7.1 最大剖面
图3和图4分别为竣工期和蓄水期坝体最大剖面内沉降及水平位移等值线。竣工期和蓄水期坝体最大沉降分别为59.7cm和63.7cm,最大沉降位于坝轴线上,位置在1/3坝高到1/2坝高之间。竣工期上、下游坝壳顺河向变形表现为向上、下游位移;蓄水期坝体大部分区域顺河向位移指向下游,上游向水平位移集中于上游坝脚附近区域。竣工期上、下游向水平位移最大值分别为11.2cm和16.4cm;蓄水期上、下游向水平位移最大值分别为4.3cm和17.1cm。受水荷载影响,心墙产生了较为明显的下游向位移,最大值为15.6cm,位于心墙上游面1/3坝高附近。
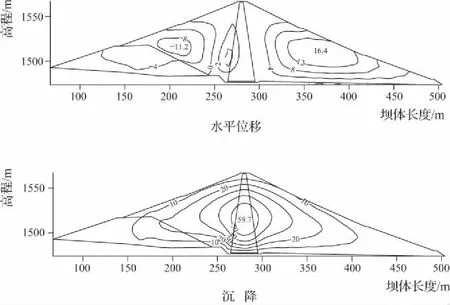
图3 竣工期坝体最大剖面沉降及水平位移等值线 (单位:cm)
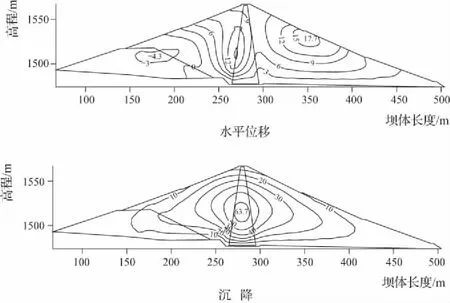
图4 蓄水期坝体最大剖面沉降及水平位移等值线 (单位:cm)
图5为蓄水期坝体最大剖面内大、小主应力等值线。

图5 蓄水期坝体最大剖面大、小主应力等值线(单位:MPa)
竣工期坝体最大剖面内大、小主应力最大值分别为1.61MPa和0.76MPa,蓄水期该剖面内大、小主应力最大值分别为1.65MPa和0.82MPa。蓄水期与竣工期相比,上游坝壳及心墙上游部位小主应力明显降低,下游坝壳及心墙下游部位大、小主应力均有所增加。从大、小主应力等值线图可看出,心墙存在一定的拱效应。
计算结果显示,施工期心墙内产生了一定的孔隙水压力,主要位于心墙中下部,最大超静孔隙水压力65.2kPa。在蓄水初期,心墙内孔隙水压力受库水压力的影响很小,心墙上游面的水压力远大于心墙内部孔隙水压力。随着运行时间的增长,超静孔隙水压力逐渐消散,心墙内稳定渗流逐渐形成。
图6为蓄水期坝体最大剖面内应力水平分布。由图可见蓄水期心墙向下游位移,心墙上游面附近坝壳中应力水平较高,最大值为0.7。坝体在竣工期和蓄水期都没有达到塑性极限状态的区域。
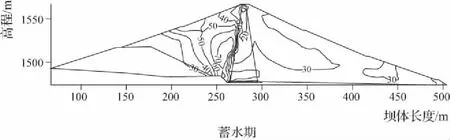
图6 最大剖面内应力水平分布 (单位:%)
2.7.2 坝轴线纵剖面
计算结果表明:坝轴纵剖面轴向位移表现为由两岸向河谷中间变形,竣工期向右岸和向左岸最大位移分别为6.3cm和6.5cm,蓄水期向右岸和向左岸最大位移分别为7.6cm和8.2cm。图7为坝轴纵剖面蓄水期的变形,蓄水期纵剖面内最大沉降为63.7cm。
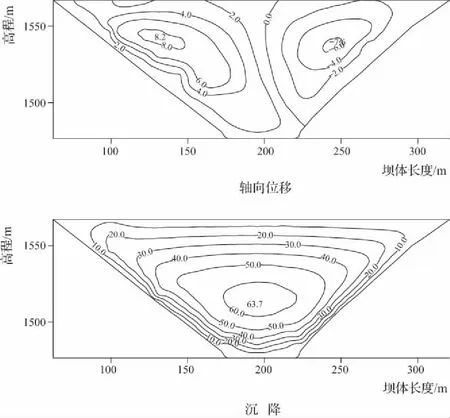
图7 蓄水期坝轴线纵剖面变形 (单位:cm)
坝轴线纵剖面在竣工期与蓄水期,岸坡附近应力水平相对较高,最大值为0.8左右。
坝轴线纵剖面竣工期、蓄水期和运行期的孔隙水压力计算结果表明:同一高程,岸坡附近孔隙水压力较河床部位高,原因为边界不透水。与竣工期相比,蓄水期孔隙水压力稍有增加,表明蓄水期心墙内部孔隙水压力受库水影响不大。但随水库运行时间的推移,心墙内超静孔隙水压力逐渐消散,稳定渗流逐渐形成,心墙内孔隙水压力主要受库水位影响。
2.7.3 心墙拱效应和水力劈裂特性
图8为心墙上游面σ1与上覆土柱应力γsH的关系曲线。计算结果显示,心墙上游面的σ1约为γsH的0.94,表明心墙虽有拱作用,但不明显,主要原因是坝壳风化料与心墙料的模量相差不大。
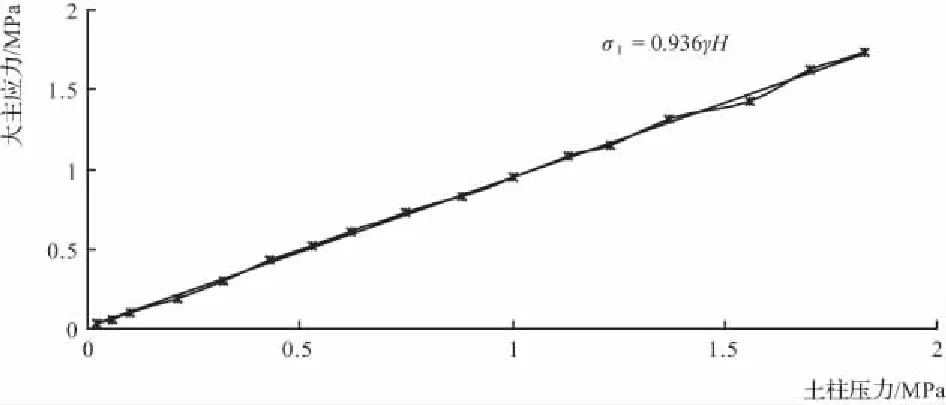
图8 心墙上游面σ1与上覆土柱应力γsH的关系曲线
心墙内的应力水平计算结果显示:心墙内应力水平总体较低,没有达到塑性极限状态的区域。心墙受坝壳拱作用的影响,蓄水期小主应力减小,但未出现拉应力区域,心墙不会产生裂缝,根据有效应力判据,蓄水后心墙不会产生水力劈裂。
3 大坝应力变形计算结果的运用
3.1 坝体心墙与两岸坡接触带的处理
坝轴线纵剖面在竣工期与蓄水期的应力水平分析结果表明,岸坡附近应力水平相对较高,最大值为0.8左右。为增加岸坡附近心墙与岸坡的变形协调性,在心墙与两岸坡接触部位填筑高塑性的黏土。
3.2 坝体沉降变形的处理
坝轴纵剖面竣工期与蓄水期的变形分析结果表明,竣工期坝体最大沉降59.7cm,蓄水期坝体最大沉降63.7cm,采取坝顶设置预留沉降高的方式进行处理,坝体各里程设置的坝顶预留沉降高如表2所列。

表2 坝顶预留沉降高
3.3 工程安全监测
为更好地监测大坝的渗流及变形,除常规观测设施外,还设置坝体变形、位移、孔隙压力、土体应变及应力、绕坝流流、岸坡地下水位观测和地震观测等。
4 结 语
阿白冲水库大坝静应力及变形计算成果表明,竣工期和蓄水期坝体最大沉降分别为59.7cm和63.7cm。竣工期水平位移最大值16.4cm;蓄水期水平位移最大值17.1cm。竣工期心墙下游向水平位移最大值15.6cm,坝轴向最大位移6.5cm;蓄水期心墙沿坝轴向最大位移8.2cm。在施工期与蓄水期的各阶段,坝体心墙内应力水平总体较低,没有达到塑性极限状态的区域,心墙虽受坝壳拱作用的影响,但其表面的三向应力均大于库水压力,均未出现拉应力区域,心墙不会发生塑性破坏和水力劈裂。将此计算成果运用于后续工程设计,采取了设置坝体预留沉降高、心墙与岸坡接触部位填筑高塑性黏土等措施,较好地保护了大坝的安全。
