基于自适应步长OBFGS算法的快速时间域全波形反演

张天泽， 韩立国， 张 盼， 胡 勇， 毛 博

(吉林大学 地球探测科学与技术学院，长春 130012)

0 前言

全波形反演利用观测地震记录的波形信息来估计地下介质的物性参数(如密度，速度和各向异性参数等)，在油气勘探，开发和地球动力学等领域有着很广阔的应用前景[1]。随着地下介质和大规模科学计算能力的提升，全波形反演的研究越来越受到重视，人们对反演所需要的优化算法也有着越来越深入地研究。

20世纪80年代，TARANTOLA[2]提出了时间域全波形反演，并指出目标函数对参数模型的梯度可以通过计算残差反传波场与正传波场的互相关得到,该方法被称为伴随状态法，它有效地避免了Jacobi矩阵的计算。PRATT等[3-4]经过推导得到FWI中的近似Hessian矩阵和精确Hessian矩阵，指出全波形反演可以利用基于Hessian矩阵的高斯-牛顿类优化算法来进行反演。但当反演较大数据体时，高斯-牛顿类优化算法的计算量很大，对存储内存的要求很高，当Hessian矩阵高度病态或非正定时，反演存在不收敛的可能性。BROSSIER等[5]将l-BFGS算法应用到弹性波反演中。l-BFGS算法通过存储固定数目的模型信息和梯度信息来计算Hessian矩阵，避免了高斯-牛顿类优化算法需要求解Hessian矩阵逆的过程[6-8]，在各类优化问题中得到了广泛地应用。以上描述的优化算法都要求在每次迭代中通过一定的步长搜索准则求解当前迭代所需要的步长，如Wolfe准则和Armijo准则等。在全波形反演的每次迭代中，这些准则要求程序不断的试探步长[9]。当步长满足特定的条件后才能进行模型的更新，而这些特定的条件通常要计算正演和求解梯度，所以依照准则的步长求解是全波形反演计算量大的重要原因之一。为了避免求解步长，王希云[10]提出了带有固定步长的基于信赖域算法的步长计算公式。J.Sun,、X.D.Chen、Narushiama等[11-14]提出了梯度类优化算法中的固定步长计算公式。马巍和胡勇[15-16]提出了基于超记忆梯度优化算法的固定步长计算公式。以上步长计算公式要求在反演的全过程固定步长进行模型迭代。在一般情况下，这些步长公式并不满足全波形反演的要求。

为提高全波形反演的精度和计算效率，笔者将OBFGS(Online-BFGS)算法应用到时间域全波形反演。OBFGS算法不要求利用准则搜索步长，避免了求取步长时的梯度和目标函数计算。这里还提出了适合全波形反演的自适应步长计算公式，该计算公式避免了利用准则进行步长的搜索，简化了步长求取的过程，能加快反演速率。笔者将这种自适应步长方法与OBFGS算法结合，应用到全波形反演中。通过数值反演，证明了基于自适应步长OBFGS优化算法的全波形反演可以提高反演精度而且可以缩短反演所需要的时间，提高反演的计算效率。

1 方法以及原理

1.1 基于高斯-牛顿算法的全波形反演基本理论

时间域波动方程的离散形式为：

A(m)d=S

(1)

式中：d和S分别为波场和震源；m表示模型的速度参数；A(m)为正演矩阵。

二维时间域全波形反演的目标函数可以表示为：

(2)

式中：dcal为数值正演得到地震数据；dobs为实际观测数据；‖g‖2表示L2范数。本文中的正演数据用时间二阶空间八阶有限差分算法计算得到[17-22]。

一般情况下全波形反演的模型更新公式定义为：

mt+1=mt+ηtpt

(3)

式中：t为迭代次数；pt和ηt分别为第次t迭代的更新方向和步长。对目标函数(式(2))进行二阶泰勒展开:

(4)

上标T表示矩阵转置，将式(4)进行最小化，可以得到高斯-牛顿法的更新方向所满足的方程：

H(m1)pt=-gt

(5)

式中:gt表示目标函数对模型的一阶导数，即梯度：

(6)

笔者利用正传波场和残差反传波场的互相关求取梯度[2]。式(5)中H(mt)是目标函数对模型参数的二阶导数，即Hessian矩阵：

(7)

所以更新方向可以表示为：

pt=-H(mt)-1gt

(8)

拓展到一般情况，模型的更新公式为：

mt+1=mt-αtH(mt)-1gt

(9)

式(9)为基于高斯-牛顿法的全波形反演模型迭代公式。

1.2 标准BFGS算法

由于对显式Hessian矩阵及其逆矩阵的计算会消耗巨大内存。在反演时，为了避免直接计算Hessian矩阵及其逆矩阵，可以用一个近似矩阵来代替真实的Hessian矩阵。拟牛顿法就是应用了这种思想。在拟牛顿法中，通常用一个矩阵Bt来代替真实Hessian矩阵(t代表迭代次数)。

标准BFGS算法是目前最流行，也是最有效的优化算法之一。该算法由Broyden、Fletcher、Goldfarb和Shanno各自独立提出[15]，隶属于拟牛顿算法。标准BFGS算法的步骤如算法1(Algorithm1)所示。

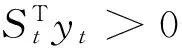
1.3 步长搜索准则

在全波形反演的每次迭代中，求取正确的步长很关键。在传统的全波形反演中通常依靠一定的步长搜索准则求取步长，这些准则通过逐步的试探步长求取最终步长。在得到一个步长之后，准则要求衡量目标函数和梯度以这个步长更新模型后，有没有一个满意的下降效果，若满足这个下降效果，则用这个步长对模型进行更新，否则就把步长按照某种比率压缩到满足要求为止。

以Wolfe准则为例，Wolfe准则要求步长满足以下条件：

(10)

式中:ρ∈(0,0.5);σ∈(ρ,1);ηt为当前步长。式(10)中第一个不等式判断目标函数的下降情况，第二个不等式判断梯度的下降情况。由式(10)可以看出，为确定合适的步长，每次算法都需要进行正演和梯度计算，这种依赖准则的步长搜索方法是全波形反演的计算量大的重要原因之一。

Algorithm1: Standard BFGS Method

Given:

·Current gradientgt)

·Line search line obeying Wolfe conditions

·Convergence tolerance ε>0

1.t:=0

2.B0=I

3. while ‖gt‖>ε

(a)pt=-Btf(m)

(b)ηt=line(f,m,pt)

(c)St=ηtpt

(d)mt+1=mt+St

(e)yt=f(mt+1)-f(mt+1)

(i)t:=t+1

4. return

--------------------------------------------Algorithm 2：Online BFGS Method

Given:

·Parameters 00

·Current gradientgt

·Sequence of step sizesηt>0

1.t:=0

2.Bo=ϖI

3. while not converged

(a)pt=-Btgt

(b)(no line search)

(c)St=(ηtpt)/c

(d)mt+1)=mt+St

(e)yt=gt+1-gt+λst

(i)t:=t+1

4. return

1.4 l-BFGS算法

l-BFGS算法同样基于对真实海森矩阵进行代替的思想，l-BFGS算法利用前n次迭代过程中的梯度变化量和模型变化量去近似海森矩阵。在l-BFGS算法中 的更迭方程为：

(11)

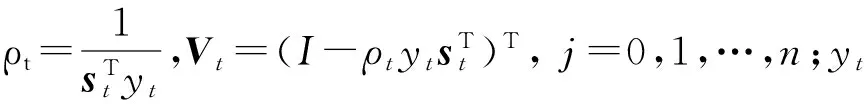
l-BFGS算法可以在只存储n+1个向量组的情况下，计算近似海森矩阵，可以加快反演的效率，但是l-BFGS算法牺牲了海森矩阵的精度。n的大小决定了在l-BFGS算法中近似海森矩阵B(n)的大小和精度[8]，因此n值的选取在一定程度上影响着l-BFGS 算法的最终反演精确度。此外，l-BFGS算法要求为海森矩阵提供一个近似的初始矩阵，初始矩阵的选择同样与l-BFGS算法的收敛性能紧密相关[6]。同BFGS算法一样，基于Wolfe准则的l-BFGS算法依旧在选择步长时需要进行梯度和目标函数的计算。这种依赖准则的步长求取方法会占用大量的内存，是传统全波形反演计算量大而且占用内存多的重要原因之一。

1.5 OBFGS算法

OBFGS对标准BFGS算法中Bt的更新公式进行了修正，并在算法中引入了新的参数，达到了使算法不依赖准则搜索步长的效果。同时OBFGS算法引入了新的参数c、λ、ϖ使得算法收敛，确保了Bt的正定性。OBFGS算法可以在合理选择固定步长的前提下，使反演在这三个参数的控制下收敛。Nicol N. Schraudolph等[11]给出了这三个参数在OBFGS算法中的取值范围，三个新参数的取值范围已在算法2(Algorithm2)中表明，OBFGS算法和标准BFGS算法的区别已经用横线画出。

在OBFGS算法中，如果ϖ=1，λ=0，c=1，OBFGS算法中矩阵Bt的更新规则就会变成标准BFGS算法的更新法则。可以看出OBFGS算法没有依照准则进行步长的搜索，避免了在确定步长的过程中计算正演和梯度，因此可以提高反演效率。在本文的数值实验中，新引入的三个参数的值为： ϖ=1，λ=1，c=1。

1.6 自适应步长设置策略

在本文中只有在目标函数不下降的情况下才会缩短步长，并以缩短后的步长直接进行模型更新进入下一次迭代，否则步长不变。

基于OBFGS算法的自适应步长全波形反演的步长设置：

1)设置步长的取值范围：ηt∈ηmin,1)。

2)自适应步长迭代公式：

(12)

κ∈[0.5,1],κ为步长缩进因子。

限制步长小于“1”是为了防止步长过大使得算法不收敛。限定最小步长是因为在反演末期，如果采用过小的步长进行反演会使得反演进展得极为缓慢。将自适应步长公式带入算法2的3(b)中就是基于自适应步长的OBFGS算法。

1.7 对比总结

通过以上对自适应步长OBFGS算法和BFGS算法的对比可以看出，自适应步长OBFGS算法不依赖步长收敛准则，可以避免在求取步长时计算梯度和目标函数，能降低反演的计算量，加快反演的计算效率。通过对自适应步长OBFGS算法和l-BFGS算法的对比可以看出，自适应步长OBFGS的海森矩阵精度更高，而且收敛效率不依赖初始海森矩阵，可以提高反演的精度。

2 数值实验

2.1 Marmousi模型反演

笔者利用Marmousi模型进行反演测试，分别用OBFGS算法和l-BFGS算法进行对比实验，突出本文算法的优势。真实模型如图1(a)所示，初始模型由真实模型的线性平滑得到，如图1(b)所示。模型的大小为50×200，网格的大小设置为40 m×40 m。震源函数为8 Hz主频的雷克子波，设置20个炮点均匀的分布在模型的顶端，接收时间为1.9 s，采样间隔为0.001 s，最大迭代次数为500次。

用基于l-BFGS算法的全波形反演进行对比，l-BFGS算法中的步长搜索方法为Wolfe准则(初始步长0.85)，OBFGS算法用自适应步长进行步长设置(初始步长设置为0.85，步长缩进因子设置为0.75)。两种优化算法反演的结果如图2所示，由图2可以看出，在不依赖准则搜索步长的情况下，在一定的误差允许的范围内，利用OBFGS算法得了更精确的反演结果。通过对比图2中的黑色箭头处的反演结果，可以看出OBFGS算法的反演结果更精确。图3展示了反演结果第90道和100道处的速度反演曲线。从图3中可以看出，基于OBFGS算法的全波形反演结果更接近真实速度。

2.2 反演效率

表1列出了可以评价算法效率的几个参数[16]：(1)迭代次数；(2)进行全波形反演所需要的计算时间；(3)CPU平均使用率；(4)计算所需的最大内存；(5)最终的反演误差。本文的反演在同一台机器上

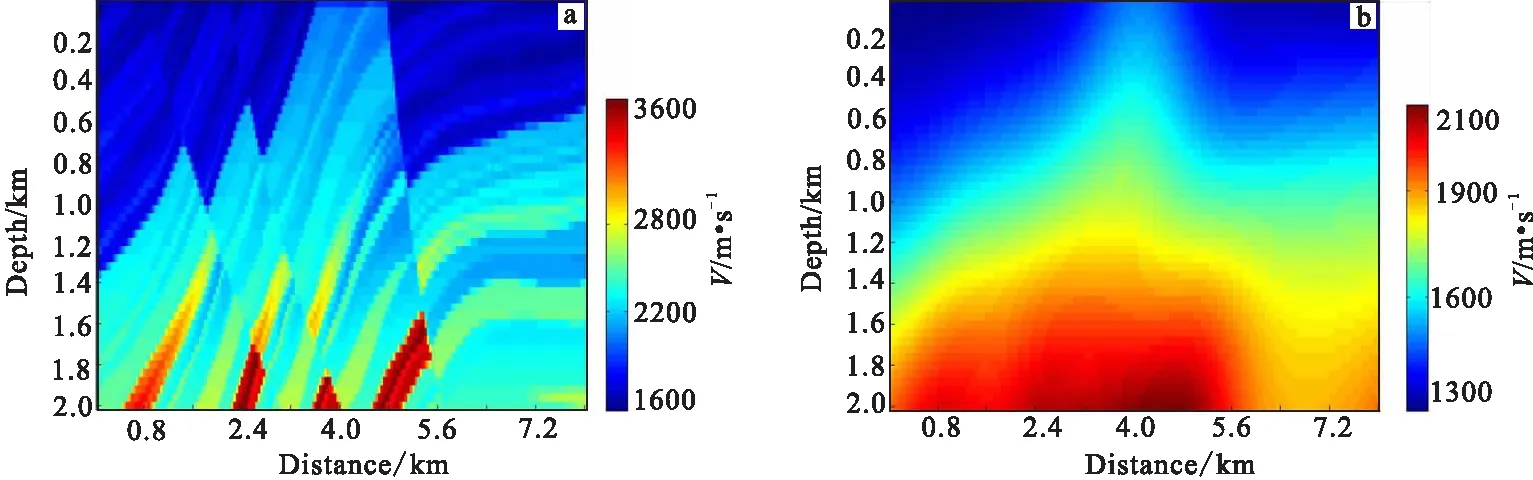
图1 模拟实验所用速度模型Fig.1 Model ased in numerical simulation test(a)真实模型；(b)初始模型

进行计算(32G内存，CORETMi3，4核处理器Ubuntu系统)，程序用MATLAB进行编译。

从对Marmousi模型进行反演的参数比较，可以看出当反演误差为1.02%时，l-BFGS和OBFGS算法分别用时71 562 s和45 629 s(初始步长均为0.85)。OBFGS算法耗时更短，提高了反演的效率。

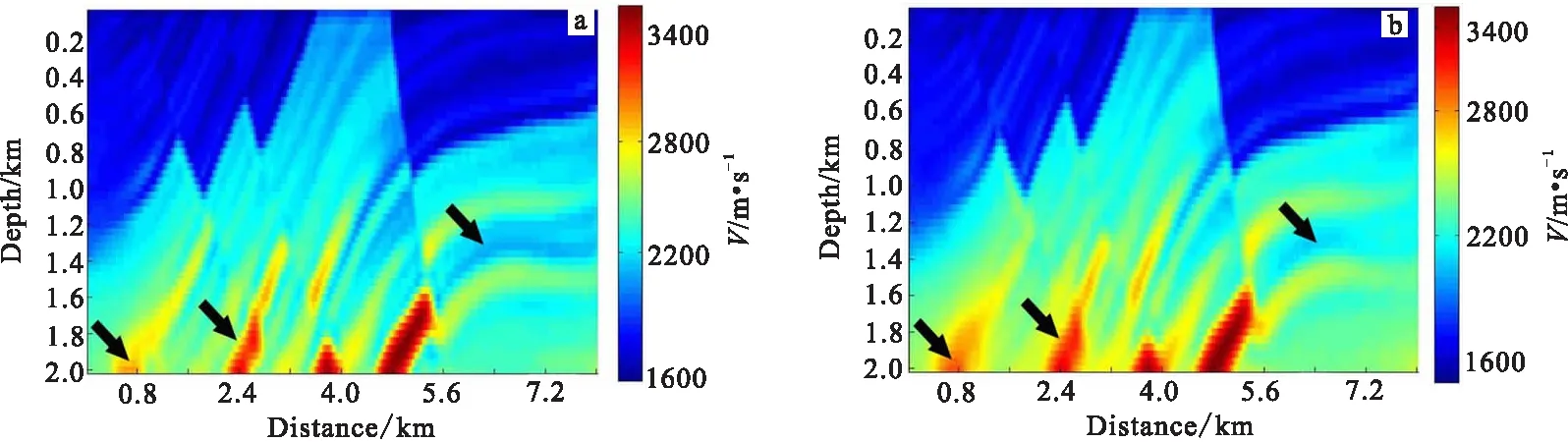
图2 基于OBFGS和l-BFGS算法的全波形反演结果Fig.2 Full waveform inversion based on OBFGS methocl and L-BFGS method(a)基于OBFGS算法的全波形反演结果；(b)基于l-BFGS算法的全波形反演结果

图3 基于OBFGS算法全波形反演和基于l-BFGS算法的全波形速度反演结果Fig.3 Velocity inversion result based on OBFGS and l-BFGS method(a)第90道；(b)第100道

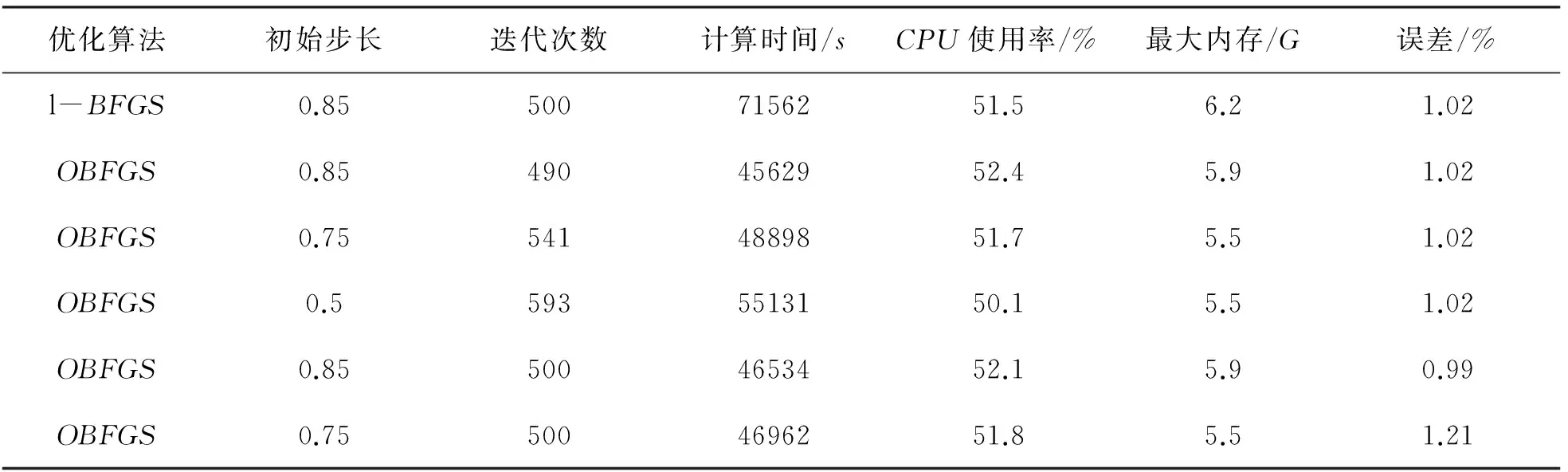
优化算法初始步长迭代次数计算时间/sCPU使用率/%最大内存/G误差/%l-BFGS0.855007156251.56.21.02OBFGS0.854904562952.45.91.02OBFGS0.755414889851.75.51.02OBFGS0.55935513150.15.51.02OBFGS0.855004653452.15.90.99OBFGS0.755004696251.85.51.21

模型更新误差计算公式为(|反演结果-真实模型|/真实模型)

从表1可以看出，在利用OBFGS算法进行反演时，如果固定反演的迭代次数，随着初始步长的变小，最终的误差会变大。利用不同初始步长进行基于OBFGS算法的全波形反演结果如图4所示。由图4可以看出，当初始步长设置较小时，最终得不到特别满意的反演效果。这是因为在相同的迭代次数相同的前提下，初始步长设置太小模型将更新缓慢，从而使反演达不到理想的效果。

图5展示了利用不同初始步长的基于OBFGS算法的全波形反演残差曲线变化图。由图5可以看出，如果用不同的初始步长进行反演，残差曲线在反演初期会呈现不同的下降趋势。相对较大的步长残差下降的更快，而小步长让曲线下降的趋势变慢。从图5中可以看出，利用基于自适应步长OBFGS算法的全波形反演策略，可以使500次迭代反演全部收敛，是一种有效的反演算法。

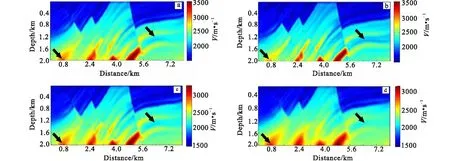
图4 不同初始步长反演结果Fig.4 Inversion result with different initial step(a)l-BFGS算法的反演结果；(b)初始步长设置为0.85的Marmousi模型反演结果;(c)初始步长设置为0.75的Marmousi模型反演结果；(d)初始步长设置为0. 5的Marmousi模型反演结果

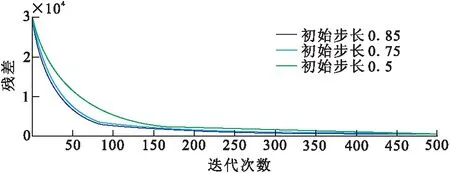
图5 基于不同初始步长的OBFGS算法的全波形反演残差曲线Fig.5 The residual of FWI based on OBFGS with different initial step size

3 结论与讨论

1)通过对OBFGS算法和l-BFGS与BFGS算法的理论对比可以看出，自适应步长OBFGS算法有着更高反演精度和计算效率。

2)通过Marmousi模型反演的结果分析表明，基于自适应步长的OBFGS算法的反演得到了更高精度的结果，提高了全波形反演的精度。

3)计算效率的对比结果表明，基于自适应步长的OBFGS算法计算效率更高。由于算法不依赖步长搜索准则进行步长求取，而是自适应的去计算步长，简化了全波形反演中的步长求取过程，提高了反演的计算效率。

从表1可以看出，步长的设置过小会使反演进行的缓慢，所以初始步长会影响最终的反演结果。如何确定全波形反演优化算法的众多参数的取值范围，从而使得反演的效率达到最高，依旧要进一步地研究。

[1] 刘国峰, 刘洪, 孟小红,等. 频率域波形反演中与频率相关的影响因素分析[J].地球物理学报，2012, 55(4)：1345-1353. LIU G F, LIU H,MENG X H,et al. Frequency-related factors analysis in frequency domain waveform inversion [J]. Chinese Journal Geophysics, 2012, 55(4): 1345-1353.(In Chinese)

[2] TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation [J]. Geophysics, 1984, 49(8):1259-1266.

[3] PRATT R G, SHIN C, HICKS. Gauss-newton and full newton methods in frequency-space seismic waveform inversion[J]. Geophysics. J. Int，1998(133): 341-362.

[4] PRATT R G. Inverse theory applied to multi-source cross-hole tomography I: acoustic wave-equation method [J]. Geophysics Prospecting, 1990, 38(3):287-310.

[5] BROSSIER R, OPERTOS, VIREUX J. Seismic imagine of complex onshore structures by 2D elastic frequency-domain full-waveform inversion [J]. Geophysics, 2009, 74(6):WCC105-WCC118.

[6] 王义,董良国. L-BFGS法时间域全波形反演中初始矩阵的选择方法[J]. 石油物探, 2014, 53(5): 545-555. WANG Y, DONG L G. Selection strategy of the initial matrix for L-BFGS method in time domain full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 545-555.(In Chinese)

[7] 王义, 董良国.基于截断牛顿法的VTI介质声波多参数全波形反演[J]. 地球物理学报, 2015,58(8): 2873-2885. WANG YI, DONG Liang-Guo.Multi-Parameter full waveform inversion foe acoustic VTI media using the truncated Newton method[J]. Chinese Journal Geophysics,2015,58(8):2873-2885.(In Chinese)

[8] 苗永康. 基于L-BFGS算法的时间域全波形反演[J]. 石油地球物理勘探, 2015, 50(3):469-474. MIAO Y K.Full waveform inversion in time domain based o limited-memory BFGS algorithm [J]. OGP,2015, 50(3):469-474.(In Chinese)

[9] KELLEY C T. Iterative methods for optimization [M]. New York: SIAM, 1999.

[10]王希云,仝建.带有固定步长的非单调自适应信赖域算法[J].应用数学,2009,22(03):496-500. WANG X Y, TONG J.A nonmonotone adaptive trust region algorithm with fixed stepsize for unconstrained optimization problems[J]. Mathematica Applicata. 2009,22(03):496-500. (In Chinese)

[11]SCHRAUDOLPH N N, YU J, GÜNTER S. A stochastic Quasi-newton method for online convex optimization [J]. Journal of Machine Learning Research, 2007(2):436-443.

[12]CHEN X, SUN J. Global convergence of a two-parameter family of conjugate gradient methods without line search[J]. Journal of Computational & Applied Mathematics, 2002, 146(1):37-45.

[13]YU Z. Global convergence of a memory gradient method without line search[J]. Journal of Applied Mathematics & Computing, 2008, 26(1-2):545-553.

[14]NARUSHIMA Y. A memory gradient method without line search for unconstrained optimization[J]. Sut J Math, 2006(42):191-206.

[15]马巍. 无约束优化问题的超记忆梯度法的若干研究 [D]. 海口：海南大学，2013. MA W. Unconstrained optimization problem of super memory gradient method of research[D]. Haikou: Hainan University, 2013. (In Chinese)

[16]胡勇,韩立国,张盼,等. 混合超记忆梯度法多尺度全波形反演[J]. 石油物探, 2016, 55(4): 559-567. HU Y, HAN L G, ZHANG P, et al. Multi-scale full waveform inversion with hybrid super memory gradient method[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 559-567. (In Chinese)

[17]MOCZO P, KRISTEK J, GLIS M. The finite-difference modelling of earthquake motions. Waves and ruptures [J]. Cambridge Univ Pr, 2014:1-365.

[18]GAZDAG J. Modeling of the acoustic wave equation with transform methods[J]. Geophysics, 1981, 46(6): 854-859.

[19]KOSLOFF D, BAYSAL E. Forward modeling by a Fourier method [J]. Geophysics, 1982, 47(10): 1402-1412.

[20]RESHEF M, KOSLOFF D, EDWARDS M, et al. Three-dimensional elastic modeling by the Fourier method [J]. Geophysics, 1988, 53(9): 1184-1193.

[21]FORNBERG B. The pseudo spectral method; comparisons with finite differences for the elastic wave equation [J]. Geophysics, 1987, 52(4): 483-501.

[22]FORNBERG B. The pseudo spectral method; accurate representation of interfaces in elastic wave calculations [J]. Geophysics, 1988, 53(5): 625-637.