基于密度峰值优化的Canopy-Kmeans并行算法*

李 琪，张 欣，张平康，张 航

0 引 言

聚类分析作为统计学的一个分支，已经被广泛研究和使用了多年。它是数据挖掘中非常重要的一部分，是从数据中发现有用信息的一种有效手段。聚类基于“相似同类，相异不同”的思想，将数据对象分组为若干类或簇，使得在同一个簇中的对象之间具有较高的相似度，而不同簇中的对象差别很大[1]。通过聚类，人们可以了解数据的分布情况，也可能会发现数据内事先未知的群组。

K-means算法是聚类分析中的经典算法，自20世纪60年代提出，已成为目前应用最广泛的聚类方法之一。K-means算法具有理论思想可靠、算法数学思想简单且易于实现、收敛速度快等优点，但算法本身存在缺陷，需要预先确定聚类数目K的值，且随机选取的K个初始中心点可能会使聚类结果产生局部最优解，算法效果受噪声点影响大。针对K-means算法存在的缺点，学者们从不同角度提出了改进方法。文献[2]提出一种优化初始中心点的算法，采用密度敏感的相似性度量来计算对象密度。文献[3]提出运用Canopy[4]算法和K-means算法结合，解决初始中心点选择问题，但Canopy算法初始参数的确定也需依靠人工选取，因此效果并不稳定。文献[5]提出了用最大距离法选取初始簇中心的K。文献[6]提出一种基于最大最小化准则的Canopy-Kmeans算法。

在学者们对传统K-means算法进行改进的同时，互联网不断发展，数据规模呈现爆炸式增长，传统的串行聚类算法已经无法满足当前处理海量数据的需求。而基于Spark与Hadoop等的开源分布式云计算平台的出现，为解决这一问题提供了很好的方案。Spark是一款基于内存的分布式计算框架，计算中通过将上一个任务的处理结果缓存在内存中，大大节省了反复读写HDFS花费的时间。

为了进一步提高K-means聚类的准确率和聚类速度，基于以上算法的优缺点，结合Spark计算框架，本文提出一种基于密度峰值的Canopy-Kmeans并行算法。利用密度峰值[7]的思想和最大最小准则，结合Canopy-Kmeans算法，降低了选取初始聚类中心时离群点对算法的干扰和陷入局部最优的概率，提高了聚类的准确性，并利用Spark框架将算法并行化，减少了聚类所花费的时间。

1 相关概念

1.1 Canopy-Kmeans算法

Canopy-Kmeans算法是一种改进的K-means算法，其算法思想分为两个阶段。第一阶段利用Canopy算法对数据集合进行预处理，快速将距离较近的数据分到一个子集中，这个子集称作Canopy。通过计算将得到多个Canopy，数据集中的所有对象均会落在Canopy的覆盖内，且Canopy之间可以重叠。第二阶段利用得到的Canopy中心点作为K-means算法的初始聚类中心点和K值，在Canopy内使用K-means算法直至算法收敛。如果两个数据对象不属于同一个Canopy，那么它们就不属于同一个簇。所以，在迭代过程中，对象只需计算与其在同一个Canopy下的K-means中心点的距离。

定义1（Canopy集合）：给定数据集合S={si|i=1,2,…,n}，对于∀xi∈S，若满cj||≤T1,cj∈ S,i≠ j}，则称Pc是以 cj为中心点、以T1为半径的Canopy集合。

定义2（Canopy中心点）：给定数据集合S={si|i=1,2,…,n}，对于Sxi∈∀，若Qm||≤ T2,T2＜T1,Qm∈ S,i≠m}， 则 称 Qm为 非Canopy候选中心点集合。其中，T1、T2为距离阈值，是预设的参数值，可以通过交叉检验得出。

1.2 局部密度

针对K-means对孤立点敏感的问题，提出一种假设。对于一个数据集，若类簇中的一个点由一些相对其局部密度较低的点围绕，那么这个点为此类簇的密度峰值点[7]。定义为：设待聚类的数据集 S={x1,x2,…,xn}，相应的指标集为 Is={1,2,…,n}，dij=dist(xi,xj)为数据点xi和xj之间的距离，当数据点为离散值时，局部密度ρi为：

式中：j与i不相等且都属于Is，函数χ(x)为：

其中dc＞0表示截断距离，根据所有点与点之间的欧氏距离小于dc值占总样本数的k来确定[8]，一般在2%～5%；dij为欧式距离。

1.3 最大最小化准则

在集合S中随机选取一个点作为种子点A，然后计算A点与集合S中所有剩余点的距离；距离最大的点选为种子点B，计算A点和B点与集合S中所有剩余点的距离，得出距离两个种子点最近的距离da与db；选取da、db中最大值的点作为下一个种子点C，可表示为：

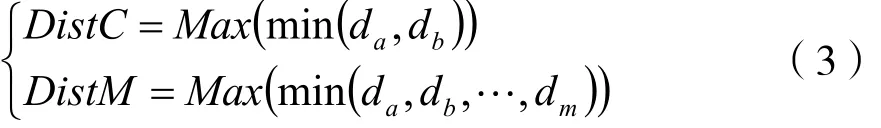
按照式（3）一直迭代至无法满足条件，即可选取出全部的种子点。

2 基于密度峰值的算法改进

随机选取的Canopy-Kmeans算法，通过初期Canopy算法对数据集的快速预聚类，解决了K-means算法的K个中心点选取问题，同时优化了算法复杂度。但是，由于距离阈值T1、T2的选取需要通过多次运行算法求出最优距离，耗费了大量时间。文献[9]对此问题进行了优化，避免了人为选取距离阈值T1、T2及Canopy初始中心点的随机选取，但并未解决选取的初始中心点可能为噪声点，从而影响算法的聚类效果。本文引入密度峰值的概念，在选取Canopy中心点前先计算数据集中密度相对较大的点，剔除低密度区域的噪声点，得到一个高密度点集合W，同时利用“最大最小化原则”使Canopy初始中心点的距离尽可能大，使算法不易陷入局部最优。

“最大最小化准则”选取的Canopy中心点呈现以下规律：当Canopy中心点个数迫近或等于集合的聚类真实值时会产生较大波动，而少于或超过聚类真实值时相对平稳[10]。同时，参考Hearst M A文本自动分段算法中的边界思想，定义[11]为：

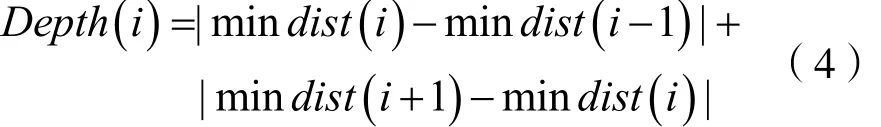
当值Depth(i)最大时，Canopy取得最优初始中心点个数，并令Canopy的T1=min dist(i)。因为已经计算出Canopy中心点，所以不再需要计算T2。综上所述，算法的实现流程图如图1所示。

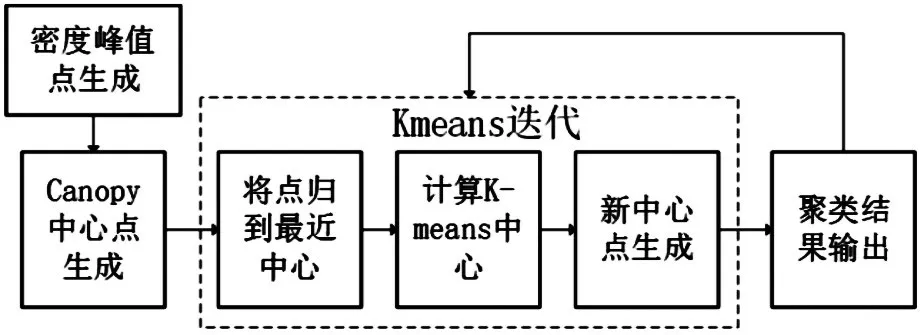
图1 基于密度峰值优化的Canopy-Kmeans流程

具体实现步骤如下：

（1）对于数据集S={x1,x2,…,xn}，通过上文中局部密度的定义，在集合S中算出每个对象的局部密度，将局部密度低的点剔除后，把剩余的点放入集合W中，并标注每个点的局部密度。

（2）将集合W中局部密度最高的密度峰值点记作初始点A，在集合W中选取距离A最远的对象记作第二个初始点B；利用最大最小准则在集合W中计算第三个点C，C的取值满足DistC=Max(min(da,db))，并求出剩余M个点，M满足 DistM=Max(min(da,db,…,dm))，且M＜（聚类个数K＜[12]）。

（3）计算Depth(i)，将M个点中的前i个对象赋值给集合U，得到Canopy中心点集合U=(u1,u2,…,ui),同时令T1=min dist(i)；

（4）输入Canopy的中心点数据集U=(u1,u2,…,ui)，将集合S中的所有点与Canopy中心点进行距离比较；小于T1的，标注该对象属于对应的Canopy，最后生成i个可相互重叠的Canopy；

（5）在Canopy中应用K-means算法进行迭代，其中初始中心点为i个Canopy中心点；迭代过程中，对象只需计算与其在同一个Canopy下的K-means中心点的距离，直至算法收敛。

3 基于Spark的改进算法并行化

Spark[13]是一个开源的基于内存的集群运算框架，在2009年由美国加州大学伯克利分校AMP实验室开发。由于Hadoop的MapReduce在运算过程中会将中间结果写入硬盘，而频繁的读写硬盘会大大增加运算时间。Spark使用内存运算技术，将中间结果写入内存，所以基于Spark的算法运算速度相比于Hadoop MapReduce大大提升。基于以上优点，本文采用Spark框架进行算法的并行化计算，流程如图2所示。

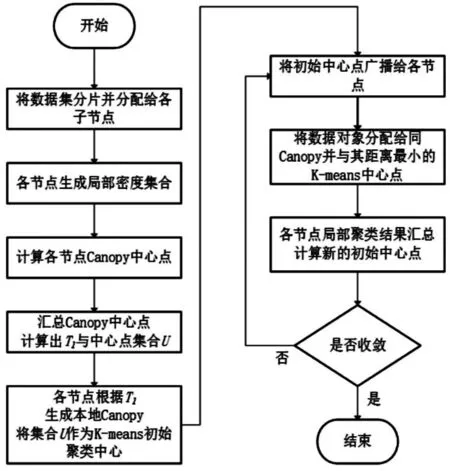
图2 算法并行流程

并行化过程中会使用Map进行局部密度点集合的求取、Canopy中心点的求取和K-means聚类。然后，使用Redcue或reduceByKey实现全局聚类，再对配置好的Spark参数后初始化环境，读取存放在HDFS上的数据集生成弹性数据集RDD并将数据向量化。对RDD使用map操作，求取两两对象间的距离，得出局部密度集合和密度峰值点。使用最大最小化准则，在局部密度集合中点求取M个初始值点。汇总各节点中的初值点到主节点，计算深度值Depth(i)得到T1，并将Canopy中心点集合赋值为K-means的Cluster中心点。对RDD执行map操作，在子节点中将距离小于T1的点划入同一Canopy。在各节点上运行K-means迭代，只需计算与中心点属于同一Canopy的点距离。综上所述，算法主要可分为以下三部分。

算法1：利用密度峰值计算局部密度集合

input：节点数据集L=(l1,l2,…,ln)

output：节点局部密度集合 W=(w1,w2,…,wm)，密度峰值点A

令集合W为空//设置初始局部密度集合

计算集合L中两两对象的距离dij；

利用dij求取dc，其中k取2%；

求出每个点的局部密度ρi；

if ρi＞ 1

将对应的点加入到集合W中；

end if

将ρ值最大的点定义为密度峰值点A。

算法2：Canopy本地中心点生成

Input：局部密度集合W，密度峰值点A，当前节点数据集规模N

output：Canopy中心点集合P=( p1,p2,…,pn)

将A点赋值给p1；

if 集合P中对象数为1

计算数据集W中距离p1最远的点B；

else

计算数据集W中数据点与集合P中所有数据点的距离，选最小值中最大者，结果放于集合P；

end if

end while

算法3：Canopy全局中心点生成

input：子节点的Canopy中心点集合P=( p1,p2,…,pn)

output：中心点集合U与T1

求取子节点汇总后集合的数据总量N

求取数据集中数据之间最小距离的最大者，将其保存到集合P'

end while

将P'中对象数赋值给k；

while j＜k

计算集合P'中的最大值并输出T1，并令集合U的值为集合P'的前i个对象

end while

算法4：K-Means迭代

input：中心点集合U=(u1,u2,…,ui)

output：K-means中心点集合U '

令U '=U；

判断U '是否改变

若U '改变，则将数据对象分配给同Canopy与它距离最小的K-means中心点；

将属于同一中心点的对象汇总，计算新的初始中心点；

输出新的聚类中心点。

4 实验结果与分析

4.1 实验环境与数据

本文实验是在Hadoop2.7.2的YARN基础上部署的Spark框架，Spark版本为2.02。实验由5台PC机组成，机器内存4 GB，CPU为Intel Core i5处理器，主频2.5 GHz，硬盘大小160 GB，操作系统版本为CentOS7。

实验一共选用五个数据集，其中4个来自UCI机器学习库，分别为Iris、Wine、Waveform和Pima Indians Diabetes，各数据集属性如表1所示；另一个来自搜狗实验室的开源分类数据库，在其中选取文化、财经和体育三个类别的文档，各选10 000篇。

表1 UCI数据集属性

4.2 结果分析

首先用传统K-means算法、文献[6]中的Canopy-Kmeans算法（下简称CK-means算法）以及本文利用密度峰值思想改进后的算法（下简称M-CKmeans算法），对前4个UCI数据集进行多次计算后求平均准确率，以对比算法的准确率，结果如图3所示。然后，再用以上几个算法对搜狗数据集的数据进行运算，结果如图4所示。

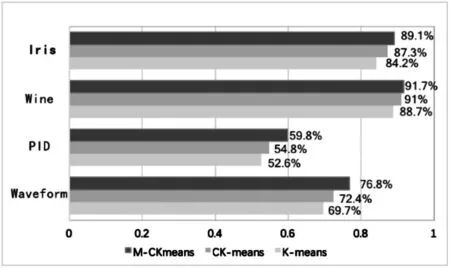
图3 UCI数据集聚类准确率

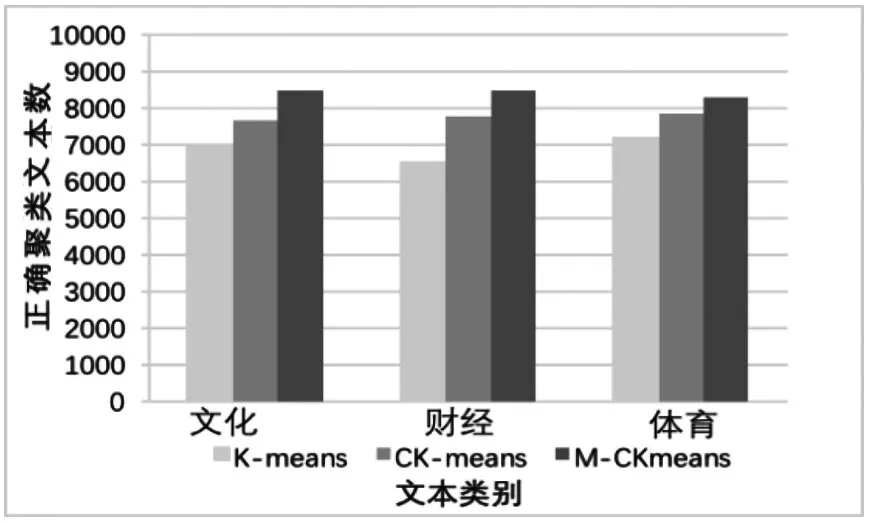
图4 文本聚类

从图3、图4可以看出，本文提出的M-CKmeans算法相比于CK-means算法和传统K-means算法，在准确率上均有一定提高，验证了基于密度峰值思想改进的Canopy-Kmeans算法的有效性。

加速比是常用来衡量程序执行并行化的重要指标[14]，本文用其来衡量算法在Spark平台下的性能。针对同一算法，用单机运行时间除以并行运行时间，就可以得到并行算法的加速比。本文将搜狗的开源数据集用CK-means与M-CKmeans算法多次运行后取平均时间，计算两种算法的加速比，结果如图5所示；再利用Iris数据集构造成60维度，不同大小的数据集（500 MB，1 GB，2 GB）对改进后的算法进行加速比对比，结果如图6所示。

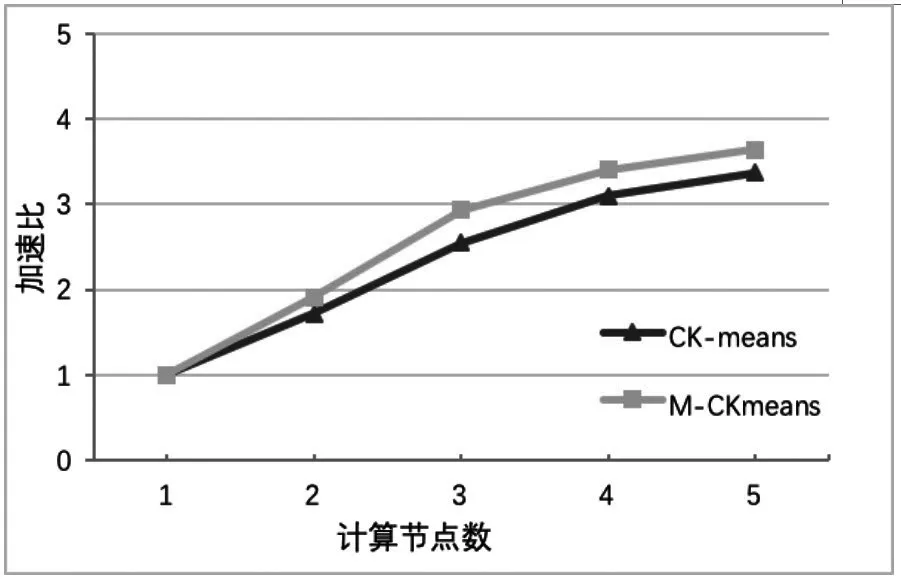
图5 相同数据集不同算法加速比

图6 不同数据大小M-CKmeans加速比

从图5可以看出，本文的M-CKmeans算法在同一数据集下，相同节点的执行效率高于CK-means算法。这主要是因为算法优化了CK-means算法的初始中心点的选取，减少了后续算法需要迭代的次数。在保持相同的数据规模下，随着数据节点数目的增加，虽然每个节点所需处理的数据量减小，但因为节点的增加还会导致节点间的通信开销增大，所以加速比的增长速度放缓。从图6可以看出，随着数据集的增加，并行后的M-CKmeans算法具有良好的加速比。综上结果证明，本文算法在Spark环境下具有较好的加速比，且并行化性能更高。

5 结 语

文中主要利用密度峰值的思想，先求出各点的局部密度，然后结合最大最小准则，优化Canopy初始中心点的选择，同时利用Spark框架改进算法并行化。实验结果表明：改进后算法在抗噪性、准确度上有明显提高，且基于Spark的改进算法能够很好地应付大量数据，具有可观的加速比。

[1] Jain A K,Murty.Data Clustering:A Review[J].Acm Computing Surveys,1999,31(03):264-323.

[2] 汪中,刘贵全,陈恩红.一种优化初始中心点的K-means算法[J].模式识别与人工智能,2009,22(02):299-304.WANG Zhong,LIU Gui-quan,CHEN En-hong.A K-means Algorithm Based on Optimized Initial Center Points[J].Pattern Recognition and Artificial Intelligence,2009,22(02):299-304.

[3] 邱荣太.基于Canopy的K-means多核算法[J].微计算机信息,2012(09):486-487.QIU Rong-tai.Canopy for K-Means on Multi-core[J].Microcomputer Information,2012(09):486-487.

[4] Rong C.Using Mahout for Clustering Wikipedia's Latest Articles:A Comparison between K-means and Fuzzy C-means in the Cloud[C].IEEE Third International Conference on Cloud Computing Technology and Science,IEEE Computer Society,2011:565-569.

[5] 翟东海,鱼江,高飞等.最大距离法选取初始簇中心的K-means文本聚类算法的研究[J].计算机应用研究,2014,31(03):713-715.ZHAI Dong-hai,YU Jiang,GAO Fei,et al.K-means Text Clustering Algorithm Based on Initial Cluster Centers Selection According to Maximum Distance[J].Application Research of Computers,2014,31(03):713-715.

[6] 毛典辉.基于MapReduce的Canopy-Kmeans改进算法[J].计算机工程与应用,2012,48(27):22-26.MAO Dian-hui.Improved Canopy-Kmeans Algorithm Based on MapReduce[J].Computer Engineering &Applications,2012,48(27):22-26.

[7] Rodriguez A,Laio A.Machine learning Clustering by Fast Search and Find of Density Peaks[J].Science,2014,344(6191):1492.

[8] 张嘉琪,张红云.拐点估计的改进谱聚类算法[J].小型微型计算机系统,2017,38(05):1049-1053.ZHANG Jia-qi,ZHANG Hong-yun.Improved Spectral Clustering Based on Inflexion Point Estimate[J].Journal of Chinese Computer Systems,2017,38(05):1049-1053.

[9] 程堃.基于云平台的聚类算法并行化研究[D].南京:南京邮电大学,2015.KUN Cheng.Parallelized Clustering Algorithm Based on the Cloud Platform[D].Nanjing:Nanjing University of Posts and Telecommunications,2015.

[10] 刘远超,王晓龙,刘秉权.一种改进的k-means文档聚类初值选择算法[J].高技术通讯,2006,16(01):11-15.LIU Yuan-chao,WANG Xiao-long,LIU Bing-quan.An Adapted Algorithm of Choosing Initial Values for k-means Document Clustering[J].Chinese High Technology Letters,2006,16(01):11-15.

[11] Hearst M A.TextTiling:Segmenting Text into Multiparagraph Subtopic Passages[M].MIT Press,1997.

[12] 岑咏华,王晓蓉,吉雍慧.一种基于改进K-means的文档聚类算法的实现研究[J].现代图书情报技术,2008,24(12):73-79.CEN Yong-Hua,WANG Xiao-rong,JI Yong-hui.Algorithm and Experiment Research of Textual Document Clustering Based on Improved K-means[J].New Technology of Library and Information Service,2008,24(12):73-79.

[13] 丁文超,冷冰,许杰等.大数据环境下的安全审计系统框架[J].通信技术,2016,49(07):909-914.DING Wen-chao,LENG Bing,XU Jie,et al.Security Audit System Framework in Big Data Environment[J].Communications Technology,2016,49(07):909-914.

[14] 陈爱平.基于Hadoop的聚类算法并行化分析及应用研究[D].成都:电子科技大学,2012.CHEN Ai-ping.Parallelized Clustering Algorithm Analysis and Application Based on Hadoop Platform[D].Chengdu:University Of Electronic Science and Technology of China,2012.