DeepPrimitive:Image decomposition by layered primitive detection

Jiahui Huang(),Jun Gao,Vignesh Ganapathi-Subramanian,Hao Su,Yin Liu,Chengcheng Tang,and Leonidas J.Guibas

Abstract The perception of the visual world through basic building blocks,such as cubes,spheres,and cones,gives human beings a parsimonious understanding of the visual world.Thus,efforts to find primitive-based geometric interpretations of visual data date back to 1970s studies of visual media.However,due to the difficulty of primitive fitting in the pre-deep learning age,this research approach faded from the main stage,and the vision community turned primarily to semantic image understanding. In this paper,we revisit the classical problem of building geometric interpretations of images,using supervised deep learning tools.We build a framework to detect primitives from images in a layered manner by modifying the YOLO network;an RNN with a novel loss function is then used to equip this network with the capability to predict primitives with a variable number of parameters.We compare our pipeline to traditional and other baseline learning methods,demonstrating that our layered detection model has higher accuracy and performs better reconstruction.

Keywords layered image decomposition;primitive detection;biologically inspired vision;deep learning

1 Introduction

The computer vision community has been interested in performing detection tasks on images for a long time.The success of object detection techniques has been a shot-in-the-arm for better image understanding.The potent combination of deep learning techniques with traditional techniques[1,2]has yielded state-of-the-art techniques which focus on detecting objects in an image through bounding box proposals.While this works well for tasks that require strong object localization,other applications in robotics and autonomic systems require a more detailed understanding of the objects in the image.Thus,another well-studied task in visual media processing is that of instance segmentation,where a per-pixel class label is assigned to an input image.Such dense labeling schemes are too redundant,and an intermediate representation needs to be developed.

Understanding images or shapes in terms of basic primitives is a very natural human abstraction.The parsimonious nature of primitive-based descriptions,especially when the task at hand does not require fine-grained knowledge of the image,makes them easy to use and a good choice.This has been explored extensively in the realms of both computer vision and graphics.Various traditional approaches exist for modeling images and objects,such as blocks world[3],generalized cylinders[4],and geons[5].While primitive-based modeling generally uses classical techniques,using machine learning techniques to extract these primitives can help us to attack more complex images,with multiple layers of information in them.Basic primitive elements such as rectangles,circles,triangles,and spline curves are usually the building blocks of objects in images,and in combination,provide simple,yet extremely informative representations of complex images.Labeling image pixels with high-level primitive information also aids in vectorizing rasterized images.

Complex images have multiple layers of information embedded in them.It is shown in Ref.[6],that human analysis of an image is always performed in a top—down manner.For example,when given an image of a room,the biggest objects such as desks,beds,chairs,etc.,are observed.Then the focus shifts to specific objects,e.g.,objects on the desk such as books and monitor;this analysis is performed recursively.When analyzing an image of a window,humans tend to focus on the border of the window if rst;the inner structure within the window and decorations are considered later.However,original object detection networks neglect this layered search and treat objects from different information layers the same.Layered detection has added value when there are internal occlusions in the image,which make traditional object detection more difficult to perform.In this work,we attempt to generate a deep network that separates multiple information layers as in Fig.1,and is able to detect the positions of the primitives in each layer as well as estimating their parameters(e.g.,the width,height,and orientation of a rectangle or the number and positions of control points of a spline).The proposed method is shown to be more accurate than traditional methods and other learning-based approaches.

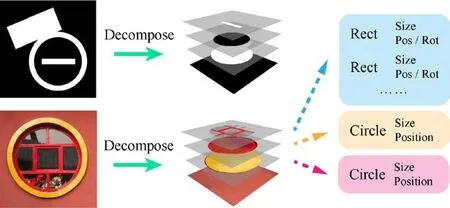
Fig.1 Motivation:given an image composed of abstract shapes,our framework can decompose overlapping primitives into multiple layers and estimate their parameters.

This paper is organized as follows.We consider related work in Section 2,and provide an analysis of the novelty of our work.Then,in Section 3,we propose a framework based on the traditional YOLOv2 network[2],to provide parameters that are fully interpretable and high-level.We also tackle the problem of regressing parameters for primitives with a variable number of unknowns.Then,we propose a layered architecture in Section 4,which can learn to separate different information layers of the image and regress parameters in each layer separately.In Section 6,we give experiments used to evaluate the performance of our network against existing traditional state-of-the-art techniques,and in Section 7,we show how this framework could be applied to image editing and recognition by components.We also discuss the limitations of our framework.Finally,in Section 9,we attempt to envisage how the framework provided in this work would help to solve the important problem of primitive-based representations,which has applications that lie at the intersection of vision,AI,and robotics.

To sum up,our contributions in this paper include:

·A framework based on the YOLOv2 network that enables class-wise parameter regression for different primitives.

·An RNN model to estimate a sequence of a variable number of control points representing a closed spline curve in a single 2D image.

·A layered primitive detection model to extract relationship information from an image.

2 Related work

Our task of decomposing an input image into layers of correlated and possibly overlapping geometric primitives is inherently linked to three categories of problems,which have been treated and studied independently in the traditional setting. Object detection and high-level vision,regression and reconstruction of geometric components such as splines and primitives,and finally,understanding relationships and layout of objects and entities are problems that provide information at different scales,all of great importance to the computer vision and graphics communities.After considering these three categories of applications,we conclude the discussion of related work with relevant machine learning methodologies,with a focus on recurrent neural networks.

2.1 Object detection and high-level vision

Among the traditional model-driven approaches to object detection, the generalized Hough transform[7]is a classical technique applicable to detecting particular classes of shapes up to rigid transformations.Variability of shapes as well as input nuances are tackled by deep-learning based techniques;faster-RCNN[8]utilizes region proposal networks(RPN)to locate objects and fast-RCNN to determine the semantic class of each object.Recent works like YOLO[1,2]and SSD[9]formulate the task of detection as a regression problem and propose end-to-end trainable solutions.We use the detection framework of the efficient YOLOv2[2]as the backbone of our framework.However,unlike YOLO or YOLOv2,as well as providing bounding boxes and class labels,our framework also regresses geometric parameters and handles the problem of occlusion,in layered fashion.

To construct high-level objects using simple primitives,Biederman[5]introduced the idea of visual composition.Recently,SCAN[10]tries to compose visual primitives in a hierarchical way and learn an implicit hierarchy of concepts as well as their logical relations using aβ-VAE network.While they build their hierarchy over concepts,our work is based on visual containment relationships for different shapes.Lake et al.[11]proposed a probabilistic program induction scheme to parse hand-writing images into several strokes and sub-strokes using a few images as training data,but their method is limited to the specific domain of hand-written characters.

2.2 Spline fitting and vectorization

Primitives and splines are widely used for representing geometry or images due to their succinctness and precision.Thus,recovering them by fitting input data is a long-standing problem in graphics.The idea of iteratively minimizing a distance metric[12—14],serving as a foundation of many studies,has been improved by either more effective distance metrics[15]or more efficient optimization techniques[16].However,most previous works fail due to lack of decent initialization,which is overcome by a learningbased algorithm in our case.It is worth noting that vectorizing rasterized images[17,18]also aims to solve a related problem.However,since previous works do not decompose an image into assemblies of clean primitives,there is a loss of high-level information about shape and layering.

2.3 Layered object detection

Multiple works have of late attempted to introduce composable layers into the process of object detection.Liu et al.[9]attempt to use feature hierarchies and detect objects based on different feature maps.Lin et al.[19]further improve this elegant idea by adding top—down convolutional layers and skip connections.However,these works only focus on how to combine features at different scales regardless of the relationships between objects and the associated layers composing the original image. The work by Bellver et al.[6]formulates detection as a reinforcement learning problem and represents an image as a predefined hierarchical tree,leaving the agent to iteratively select subsequent parts to look at.The work most relevant to ours is CSGNet[20],a recursive neural network model which generates a structured program defining the relationships between a sparse set of primitives.However,the possible positions and sizes of the primitives are limited to the size of a finite action space. In contrast,our work allows more detailed transformations of primitives,and our layered representation is less prone to redundancy.

2.4 Recurrent neural networks

The recurrent neural network(RNN)(and its variants LSTM[21],GRU[22])is a common model widely used in natural language processing which has recently been applied to computer vision tasks.One key inspiration for our work is polygon-RNN[23],in which a sequence of vertices forming a polygon is predicted in a recurrent manner.One of the key differences in our work is that we aim to abstract the simplest types of representation on different layers,based on general splines instead of polylines,or interpolating cubic Bézier curves as in the polygon-RNN.

The discussion above only samples the studies most relevant to our work.There are many other relevant areas such as image parsing,dense captioning,structure-aware geometry processing,and more.Despite richness of relevant works across a wide range which manifest the importance of the topic,we believe that the problem of understanding images as abstract compositions is underexplored.

3 Basic model

In this section,we propose a framework based on a standard modification of the YOLOv2 model[2],inspired by Ref.[24],to perform parameter regression.The parameters regressed by the model,as opposed to those in Ref.[24],are fully interpretable and highlevel.

3.1 Adapting YOLO for parameter regression

The primary idea of this model is to extend the architecture of the state-of-the-art object detector YOLOv2 to detect primitives in an image,and in addition,to estimate the parameters of each primitive.The deep neural network architecture is capable of extracting more detailed descriptors of detected objects,as well as the bounding box location.Providing additional structural information about the object to the YOLOv2 architecture aids in augmenting the learned features.

The YOLOv2 network in the original paper consumes an entire image and segments it into a grid of sizeS×S.Each square in the grid can contain multiple primitives.The networks model this multiplicity by containing up toBpossible anchors(primitives in this case).Thus,traditional YOLOv2 networks learnS×S×B×(K+5)different parameters;theK+5 term arises since,in addition to the class labels for theKdifferent primitive classes,the network also predicts 1 object probability value and 4 bounding-box related values[2].While regressing parameters for the bounding boxes,the regressor needs to predictMextra variables for each bounding box being predicted.TheMvariables are the total number of possible parameters from all different primitive categories.This increases the number of parameters predicted by the network to S×S×B×(5+K+M).

To achieve this end,a new loss term is added to the loss function previously proposed in Ref.[24].The new term,Lp,feeds information about the primitive parameters into the network.This term is defined as

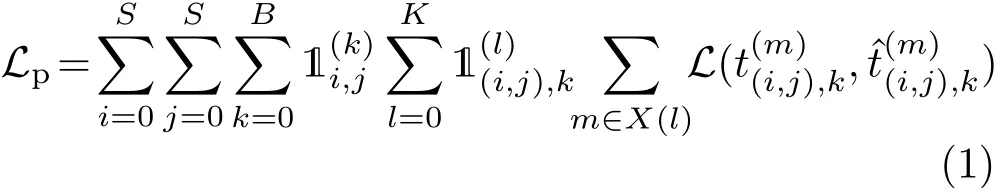
3.2 De finition of primitive parameters

Primitives with fixed number of parameters.Simple primitives like rectangles or circles have fixed numbers of parameters,and so the values of these parameters can be used directly as ground truth for training.For parameters lying within[0,1],we can further increase the network training stability by applying a sigmoid function to the network output to constrain the estimated parameters.Readers are referred to Section S1 in the Electronic Supplementary Material(ESM)for detailed definitions of primitive parameters.

Primitives with variable number of parameters.Some of the primitives discussed in this paper,including closed B-spline curves,have a variable number of control points.This permits primitives to represent different kinds of shapes,but it is not compatible with the previously defined model.This incompatibility is solved by learning a fixed-length embedding of the control point positions.In addition,a recurrent neural network(RNN)is appended to the model,to serve as a decoder to output the control points in a sequential manner.At time stepi,the model predicts the position of the ithcontrol pointci,and a stop probabilitypi∈[0,1],that indicates the end of the curve.We apply crossentropy life loss to the stop probability while training the RNN.

The loss functions for the RNN-based model must be designed with care. Naively,one can use a simple mean-squared error(MSE)loss for control point position prediction and a cross entropy loss for probability prediction.However,this only handles the situation where the sequence of control points is fixed and well-defined.Note that every point in the control point sequenceC=(c1,...,cN)of a closed spline curve can be viewed as the starting point of the sequence.Thus,in order to predict a control point sequence invariant to the position of starting point,a circular loss similar to that used in Ref.[23]is defined as follows:

whereLis the MSE loss,Gkis the ground truth control point sequence rotated by k places,i.e.,if gidenotes theithcontrol point in the ground truth,then Gkis the sequence(gk,···,gN,g1,···,gk-1)andis the inverse sequence ofGk.In this way,the ground truth sequence that leads to minimum MSE loss is considered to be the target sequence,making the loss function rotation-invariant.Also note that the introduction ofguarantees the loss to be invariant to clockwise and anti-clockwise sequencing.

4 Layered detection model

4.1 Layered detection

We use a layered model to capture the nested structure of primitives in an image.The idea is inspired by two observations.Our first observation is from how multiple layers in design tools,such as Adobe Photoshop and Illustrator,can help create a vector graphics image.With layers,artists can plan the arrangement of items in the space in a top—down manner.This fact that all vector icon images can be decomposed into multiple layers,as shown in Fig.1,serves as inspiration to extend the model proposed in Section 3 to include layered detection.Secondly,for the detection of each layer,it allows one to focus on a specific part of the image,instead of working on the entire image.For example in Fig.1,the white rectangle in the lower-right of the image is completely inside the black disk:one can focus in the interior of the disk where the only accessible primitive is the rectangle.

However,training separate networks for different levels of detection is a redundant and time-consuming process,since intuitively,the parameters regressed by these networks are likely to be related.Therefore,we propose a layered detection model to perform this regression task,thereby making the training process both faster and cognizant of previous learning.We perform region of interest(RoI)pooling[25]on the intermediate output of our network.This enables us to extract regions in the image to focus on,to perform detection at the next level.

4.2 Architecture

After an image is forwarded through the backbone network,simple post-processing steps including thresholdingand non-maximalsuppression are performed to obtain the final prediction results.The backbone network is the previously discussed YOLO network with modified loss;the difference lies in that the backbone network is intended to only predict primitives in the top layer,i.e.,the outermost primitives in the image.Following this,the coordinates of the bounding boxes of detected primitives are fed into an RoI pooling layer.The RoI pooling layers consume the intermediate output of the network and pool it into a uniform sized feature map for detection following the layering.Figure 2 illustrates this model.

Specifically,the architecture of the backbone network can be treated as multiple consecutive modules,which contain several convolution layers with ReLU activation;each module is combined with pooling layers.We denote the modules byf1,···,fM(from shallow layers to deep layers).The deepest layer fMhas outputJ1that is processed by the detection blockd1.Subsequent detection blocksdiprocess the output of convolutional layerfM-i+1.We do not use the whole feature mapJias the input todi,but instead,we crop the feature map using the prediction results fromdi-1and resize it to a uniform size.In this way,the layering is represented explicitly by cropping within the interior of an image.This model can be expressed as

Fig.2 The detection process in our layered model.Cuboids denote input images or feature maps.Dark blue arrows,dark green arrows,and dark purple arrows represent conv layers,RoI pooling layers,and detection blocks,respectively;notation is consistent with that in the text.The final output of our network is a layered primitive tree containing both shape information and layer information.

whereR[J;B(i)]represents feature mapJcropped using bounding box information fromB(i)which is fed to an RoI pooling layer to obtain a uniform size output for future processing.

Lower level feature maps are employed for deeper layer detection since deeper layer primitives are usually smaller in size and thus clearer feature maps are required to perform accurate detection. For consistency within different regions in image,we perform training using local coordinates within the parent bounding box as the ground truth forB(i).For example,consider an image with a rectangle inside a circle.Then,the ground truth coordinates for the rectangle should lie within the local coordinate system with respect to the circle.Therefore,predicted coordinates are transformed before calculating the loss functions.These local coordinates are used for ground truth since RoI pooling is known to capture partial information in the image,as testified by faster-RCNN[8]. Meanwhile,since there are multiple layers of convolutional operations,the feature map can encode some information outside the bounding box,thus providing the model with the capability to correct mistakes made in outer layers,by considering both local and global information while making detections in inner layers.

It is worth noting that the information passed from higher to lower layers is not simply restricted to the explicit bounding box position.The feature map in shallower convolutional layers is used to predict both higher and lower level primitives(e.g.,in Fig.2,J2affects bothB(1)andB(2)).Although we only pass the bounding box information explicitly,knowledge from higher layers can be passed implicitly via these related feature maps.

5 Implementation

In this section,we present our implementation details.

5.1 Primitive and parameter selection

Four types of primitives are used in our experiments:rectangles,triangles,ellipses,and closed spline curves.We observed that the predicted bounding box position is usually more accurate than the regressed parameters.Hence,a local parameter with respect to the bounding box is defined for each primitive so as to be able to perform better reconstruction.Readers are referred to Section S1 in the ESM for detailed descriptions of the parameters used.

5.2 Network architecture

Our code is adapted from an open source PyTorch implementation①https://github.com/longcw/yolo2-pytorch.The backbone network uses the Darknet-19 architecture configured as in Redmon and Farhadi[2].We set the depth of our layered detection model to 3,using three detection blocks.Detailed configuration of detection blockdi(i=1,2,3)is provided in Section S2 of the ESM.

5.3 Training

The entire hierarchical model can be trained fully endto-end.Additionally,we adopt a method similar to scheduled sampling[26]to enhance training stability and testing performance.The predicted information B(i-1)from level i-1,which is fed into level i,is substituted by the ground truth value for leveli-1 with probabilityp.The value ofpis set to 0.9 in the first 10 epochs and is subsequently decreased by 0.05 every 2 epochs.

An RNN decoder model is pre-trained separately to regress a fixed length embedding for control point positions.While training this RNN model,the grid numberSis set to 1 in the YOLOv2 detection framework and the features of closed spline curve images are extracted with our backbone Darknet-19 network.The pre-trained RNN decoder learns to decode the fixed length embedding and output positions of control points sequentially.When the layered model is being trained,the value of the embedding is used as direct supervision. In the first 5 epochs,the embedding is supervised and in subsequent epochs,the network is trained with the positions of control points instead.Note that the RNNs share the same weights across different levels of the hierarchy.

5.4 Data synthesis

Following previous works[10,27],we use synthetic datasets due to the lack of annotated datasets.The hierarchical model was trained with 150,000 synthetic pictures of size 416×416.When we generated the training data,we kept the containment relationships across layers;there may be multiple primitives in each layer.The number of primitives in a single image is restricted to 8,the maximum number of layers to 3,and the number of control points of closed spline curves varies from 5 to 7.In order to test the robustness of our method,noise was added to the shapes of the primitives,as well as hatching patterns for primitives and some skewing of the image itself.Selected dataset images are shown in Fig.3.

6 Experiments and results

6.1 Ablation study for circular loss

During the pretraining process for the RNN decoder to predict control point positions,we compare the training and validation losses using two different loss functions,i.e.,the previously definedLcircand a simple MSE loss.As shown in Table 1,training with circular loss leads to better convergence loss and thus better prediction results.Figure 4 shows two examples comparing the prediction results given the same curve image as input.We found that using circular loss eliminates the ambiguity of starting point and clock direction in the training data,and leads to more accurate fitting results.

Table 1 Error and accuracy measures during training and testing with two different loss functions.Loss denotes the MSE distance between the ground truth and predicted positions of control points(distances are normalized to lie in the unit interval).#Point Acc.denotes the frequency of predicting the number of control points correctly

6.2 Comparisons to other methods

Although our model detects primitives in a layered manner,simple object detection measurements including precision and recall rate(or mAP for methods with confidence score output)can be applied to test model accuracy.Meanwhile,we define our reconstruction loss as the pixel-wise RMSE between the input picture and the re-rendered picture using the predicted results from the network.There are multiple approaches to shape detection;we set up 5 independent baselines for comparison.The first two baselines are traditional methods while the last three are learning-based approaches:

·Contour method.In this method,edge detection is first applied to the input image; each independent contour is separated. A postprocessing approximation step is then employed to replace almost collinear segments with a single line segment with a parameterqcontrolling the strength of approximation.The type of shape is determined by counting the number of line segments(i.e.,its number of edges).This method is implemented usingfindContoursandapproxPolyDPfunctions of OpenCV[28].

·Hough transform[29].This is widely used to find imperfect shape instances in images by a voting procedure in parameter space.For rectangles and triangles,whose edges are straight line segments,we first use Hough line transform to detect all possible lines and then recover the parameters of the primitives by solving a set of linear equations.For ellipses,we use the method described in Ref.[30].

Fig.3 Examples drawn from our synthetic training dataset.For the Pure dataset,we synthesized simple binary images for training.The Pure+Noise dataset modified the Pure dataset by adding noise and random affine transformations to each image.The Tex.(short for“Textured”)dataset allows testing of the robustness of shape detection methods by adding hatching patterns to the shapes.The Textured+Noise dataset imitates real world hand drawn shape pictures.The Natural dataset imitates colored versions of real world images.

Fig.4 Two closed spline curve fitting cases using circular loss and MSE loss.

·CSGNet[20].In 2D,this takes a single image as input and generates a program defining the shapes presented.This model allows for more complex Boolean operations between shapes but the sizes and positions of the primitives are highly discretized.We use the post-processed(optimized)top-1 prediction as the output of this algorithm.

·Flat model.This method uses a learning approach trained using the YOLOv2 architecture. The ground truth of the detector is directly set to all primitives in the canvas,regardless of their hierarchical information.

·Recursive model.We train only one detector to detect the primitive in the first hierarchy(i.e.,the outermost primitive at the current level).Once the detector successfully detects some primitives in the current level,we crop the detected region,resize the cropped region to the network input size,and feed the image into the same network again.

Results from these different models are compared in Table 2(precision—recall—reconstruction comparison)and Table 3(primitive—reconstruction comparison).Some of the prediction results from different methods are shown in Fig.5 using the same input in each case.

The contour method with smallqvalue traces the pixels on the contour precisely but ignores the high-level shape information of the shape boundary,leading to a high reconstruction performance but low precision and recall accuracy in shape classification tasks.Using a greaterqvalue simply approximates continuous curves with polygons,leading to poor reconstruction performance.It is also observed that the contour method cannot separate overlapping primitives since it only attempts to detect boundaries in images.The Hough transform-based method for line segment detection and circle detection requires a careful choice of parameters;it generally leads to higher recall values than the contour method.This method partially solves the overlap problem by extending detected line segments and finding intersections,but cannot effectively distinguish extremely short line segments and segments of a circle.

The above problems can be overcome by learningbased models.Learning-based models generally have better performance across all different datasets and the gap in performance widens as we add more noise to our dataset,which is partially due to the fact that the learned features extracted from the image using our data-driven method are more effective and representative in comparison to hand-crafted features of traditional methods.Despite the feature improvement,the absence of effective shape and relationship representations can be fatal to the final detection results.Using CSGNet[20],the possible locations and sizes of primitives are restricted due to the size limitation of the action space.In order to compose the target shape,redundant shapes and expressions are generated.

Table 2 Precision,recall,and reconstruction loss measures using various methods as described in Fig.3.Prec and Recall denote the precision and recall values as percentages respectively while Recon measures the RMSE loss between the original picture and the reconstructed picture using the layered prediction results

Table 3 Average precision(AP)measures of learning-based shape detection methods.Values are presented in percentage

Fig.5 Detection results examples.Shapes detected at different levels are marked in different colors:level 1,pink;level 2,orange;level 3,blue.For the flat model,there is no predicted layer information,so all shapes are marked in green.

Other learning-based baselines fix this with simple containment representations but problems still occur due to lack of layering or incorrect layering.The flat model detects almost all primitives regardless of their layer.However,in cases where two primitives of the same kind(e.g.,concentric circles forming an annulus)overlap,the post-processing step(nonmaxima suppression)eliminates one of them and predicts the median result,which is undesirable.It is also difficult to reconstruct the original image using the detected primitives due to the loss of layering information.In the recursive model,the layering information is preserved,but if the detection in an outer layer is not accurate enough,the error snowballs and the inner layer primitives cannot be well-reconstructed.Unlike the baselines,our method can extract high-level shape information as well as containment relationships.Our model outperforms the others both quantitatively and qualitatively,except for the reconstruction loss.However,after appending a simple local optimizer to our model,denoted Our model(optimized)in Table 2,the reconstruction loss is further decreased.

The trained model was applied directly to Google Material icons[31](lines 1—4 of Fig.6,using Pure model)and a small real world dataset containing 150 images selected from the PASCAL VOC2012 dataset[32]and the Internet(lines 5—8 of Fig.6,using Natural model).To the best of our knowledge,no public dataset exists that provides ground truth annotations at geometric primitive level.So we have manually annotated the 150 images from this small real world dataset.Testing using our trained model reached an mAP(the metric used in all experiments)of 54.5%.Readers are referred to Sections S3 and S4 in the ESM for further results.

Fig.6 Selected test results for our layered detection model.In each pair of columns,the left picture shows the original input image as well as the detection result while the right picture reconstructs the input image using the detection result(different instances of primitives within the same hierarchy vary slightly in color for clarity).More test results are available in Sections S3 and S4 in the ESM.

While DeepPrimitive manages to decompose the real world images into relevant primitives,it is to be remembered that this is not the primary focus of our work.Our current model is trained only on synthetic images,but adapting synthetic images to real images with domain adaptation techniques is one trend in the vision community.A few recent vision papers have been trained and tested on purely synthetic datasets(e.g.,Ref.[27]).

7 Applications

Once an image has been decomposed into several layersand high-levelparametersdefining the primitives in the image acquired,one can utilize this information for a variety of applications.In this paper,we demonstrate the use of these parameters in two example applications.

The first application we present is image editing.It is usually very difficult for an artist to modify the shapes in a rasterized image directly.With a low reconstruction loss,our model can decompose an image into several manipulable components with high fidelity and flexibility.For example,in Fig.7,it is easy for an icon designer to modify parameters of the shapes,changing the angle between the hands of the clock,or tweaking the shape of the paint brush head.For real world images in Fig.8,we can directly manage the position of the parts in an image using high-level editing tools(e.g.,as in Ref.[33]).

Fig.7 Image editing on a rasterized image at a primitive level.Primitive detection is performed on the image,followed by editing of the primitives.

Another potential application is recognition-bycomponents[5].Usually,state-of-the-art classifiers based on deep networks need very much data for training,and its lack hampers accuracy. Once primitives in an image have been recognized,one can easily define classification rules using the layered information obtained.Additional training data is not needed and only a single shape detection model has to be trained.The idea is illustrated in Fig.9.Given an image,pre-processing steps such as denoising and thresholding are performed to extract the borders of shapes.The proposed model is then applied to detect the primitives and generate a shape parsing tree(in XML format in the figure for demonstration purposes),with which a handcrafted classifier could easily predict the class of an object in the image by top—down traversal of the tree.

8 Limitations

As an explorative study aiming to understand and reconstruct images as primitives composed layer-wise,there are several limitations left to be resolved in future work.For images with highly-overlapping primitives within the same layer,our model cannot distinguish between them:the output will either be a single primitive or misclassified primitives.Our model discovers only containment relationships:if one higher-level primitive intersects multiple lowerlevel primitives,duplicate detections of the higherlevel primitive are possible.The last two images of line 4 in Fig.6 demonstrate such failures.These limitations restrict the layer decomposability of our model.Meanwhile,only synthetic images are used for training.Annotated real world data would make the model more generalizable.

Fig.8 High-level image editing of real world images based on detected primitives.The first two columns of each group show the original image and its layered decomposition while the last two columns of each group show manipulated results.

Fig.9 Recognition-by-components demonstration using our proposed hierarchical primitive detection model.

9 Conclusions

This paper demonstrates a data-driven approach to layered detection of primitives in images,and subsequent 2D reconstruction.As noted,abstraction of objects into primitives is a very natural way for humans to understand objects. As artificial intelligence moves towards performing tasks in human-like fashion,there is value in trying to perform these tasks in the way a human would.

Such tasks often also fall in the intersection of robotics and computer vision,e.g.,in the cases of autonomous driving and robotics.In such tasks,building in environment-awareness into cars or robots based on their field of vision is key,and primitivelevel reconstruction would be useful. Primitivelevel understanding would also help in understanding physical interactions with objects in manipulation tasks.While there are many such avenues where this understanding could be applied,there is a lack of open datasets for training on real world data.A good direction for future study would involve learning tasks of an unsupervised or self-supervised kind.

Acknowledgements

Chengcheng Tang would like to acknowledge NSF grant IIS-1528025,a Google Focused Research award,a gift from the Adobe Corporation,and a gift from the NVIDIA Corporation.

Electronic Supplementary MaterialSupplementary material with detailed experimental configuration and results is available in the online version of this article athttps://doi.org/10.1007/s41059-018-0128-6.