Acquiring non-parametric scattering phase function from a single image

Yuki Minetomo,Hiroyuki Kubo(),Takuya Funatomi,Mikio Shinya,and Yasuhiro Mukaigawa

Abstract Acquiring accurate scattering properties is important for rendering translucent materials. In particular,the phase function,which determines the distribution of scattering directions,plays a significant role in the appearance of a material.We propose a distinctive scattering theory that approximates the effect of single scattering to acquire the non-parametric phase function from a single image.Furthermore,in various experiments,we measured the phase functions from several real diluted media and rendered images of these materials to evaluate the effectiveness of our theory.

Keywords scattering;phase function;measurement;rendering

1 Introduction

Achieving realism is one of the main goals in the field of computer graphics(CG).An effective way to create realistic CG is to reproduce the optical properties of materials,such as reflection and scattering.Reflection effects are represented using the bidirectional reflectance distribution function(BRDF)which describes the distribution of reflected light with respect to incident light.For translucent materials,scattering effects are also significant in representing their appearance when rendering[1,2]and editing[3,4]them.Scattering effects are represented using three parameters:the extinction coefficient,the scattering coefficient,and the scattering phase function.The extinction coefficient describes the ratio of light attenuation due to scattering or absorption in translucent materials.The scattering coefficient describes the ratio of scattering of the attenuating light.The scattering phase function describes the angular distribution of scattered light.In creating realistic CG,it is important to acquire the optical properties of real materials.

In previous work,many methods have been proposed to acquire the BRDF.In regard to parametric models,the work of Phong[5],Ward[6],Lafortune et al.[7],and He et al.[8]are well known in the field of CG.These parametric models represent the BRDF using a few parameters.However,none are versatile enough to represent real objects,so other methods have been studied to measure BRDF and represent it using a non-parametric model.A gonioreflectometer is a well-known device for acquiring non-parametric BRDF.It makes direct measurement possible by changing the light position and observation point.Müller et al.[9]and Ben-Ezra et al.[10]developed measurement systems with multiple light sources and sensors.Marschner et al.[11]and Matusik et al.[12]measured the non-parametric BRDF using an object with uniform reflection properties.Mukaigawa et al.[13]and Ghosh et al.[14]developed measurement systems using a projector and mirror.

There is also much research on acquiring scattering properties.Donner and Jensen[15],Jensen et al.[1],Papas et al.[16],and Munoz et al.[17]estimated scattering properties based on the diffusion approximation;this approximation assumes an optically dense medium for which high-order scattering is dominant.It can describe complex scattering effects very simply,and therefore,many studies employ this approximation.Gu et al.[18]estimated scattering properties based on the single scattering approximation.This approximation considers optically thin media for which single scattering is dominant,as for example in a dilute medium.It enables direct measurement of scattering properties.Khungurn et al.[19]estimated scattering properties based on appearance matching.Other approaches assume specific scattering effects such as high-order or single scattering.However,this method allows the estimation of scattering effects to all orders including high-order and first-order.While most researchers are more interested in measuring scattering properties,there is scant research focusing on the phase function.According to previous research[20],the phase function is wellknown to be significant in reproducing material appearance in CG.Like the phase function,the BRDF also describes the distribution of out-going light and has a significant role in the appearance of materials.Although recent studies on measuring BRDF have adopted a non-parametric representation,phase function measurements are usually not undertaken,or alternatively parametric models such as the Henyey—Greenstein(HG)phase function[21]are adopted in many instances.The parametric model,in an approximate sense,can easily reproduce phenomena from a small number of parameters.However,it sacrifices physical plausibility and there are limitations in its ability to generate correctly a realistic appearance of actual media.Mie scattering is a well-known scattering phenomenon and is known to have numerous peaks in amplitude.Parametric models cannot represent such complex scattering.There are however only a few methods for acquiring the non-parametric scattering phase function.Here,we propose a method for acquiring the nonparametric phase function of a real medium from a single image.Our method is based on a distinctive formulation of the relationship between the single scattered field and the phase function.To validate our method,we used a projector—camera optical system enabling the phase function to be measured from a single image captured with simple equipment.In summary,the contributions of this paper are as follows:

·A formulation of single scattering fields is proposed.

· A simple method is proposed to measure the non-parametric phase function from just a single image.

· Experiments using simple equipment have been performed demonstrating the technique.

2 Related work

In this section,we consider related work from the viewpoint of the phase function.Jensen et al.[1]obtained scattering properties using the diffusion approximation.The method assumes that multiple scattering is occurring within an optically dense medium,so that certain characteristics of the medium can be estimated from scattering properties.Some studies adopt this approximation to acquire scattering properties.However,in this approximation,the phase function can be directly measured by the method.Therefore,the phase function is not mentioned by the above paper.Despite not using the diffusion approximation,there are several other studies that have not considered the phase function.Fuchs et al.[22]proposed a method for acquiring scattering properties from time-varying participating media such as smoke using a line scanning system.They consider the phase function as isotropic.

In other research,a basic parametric model such as the HG function is used to represent the shape of the phase function.In this way,it represents a variety of scattering distributions using a single parameter.Narasimhan et al.[23]measured scattering properties using the single scattering approximation.Their method estimates scattering properties by minimizing an error function for an image formulation model from a single scattering observation.They used the HG function in their image formulation model.Mukaigawa et al.[24]analyzed the scattering light transport in translucent media.For this purpose,they separated scattering at each bounce and recursively estimated the scattering light transport for each bounce based on a forward-rendering process.In forward rendering,they used the HG function.However,the HG function is unsatisfactory when it comes to reproducing the properties of actual media[20].

Other research demonstrates moreflexible parametric models than the HG function.Kattewar et al.[25]proposed the developmental HG function using the linear combination of two HG lobes.It can represent scattering of a type in which both forward and backward scattering are mixed.Gkioulekas et al.[26]proposed to represent the phase function as a convex combination of a tent function and a weight factor.This function is moreflexible than the HG phase function.To ensure estimation is accurate,it needs many observations using a special optical system that requires a complex calibration process.However,to reproduce the appearance of real objects,a non-parametric model is more suitable than a parametric model.

Whereas the above methods adopted a parametric model for representing the phase function,other methods adopt a non-parametric approach.Hawkins et al.[27]measured scattering properties by developing a laser-scanning system.Because there is no model for the phase function,their system directly measures the phase function from a wide range of directions.To realize the measurement,they built special equipment with a conical mirror,which is complicated and not easy to reproduce.In addition,scattering from some directions could not be measured,specifically at scattering angles≈0 andπof the phase function.In these instances,an optical element used in the measurement blocks the path of the ray.Moreover,it is not easy to split the measurement into scattering and direct components.

3 Formulation of scattering field

In this section,we propose an alternative formulation of the scattering field that allows acquisition of the non-parametric scattering phase function in a oneshot measurement.The main symbols used in the equations are listed in Table 1.Consider the situation shown in Fig.1;a perpendicular incident ray scatters in a uniform participating medium.For simplicity of formulation,let us assume:

· the medium is optically thin,and therefore single scattering is dominant,

· the medium produces forward scattering,and

· the phase function of the medium is axially symmetric,depending only on the angle between the directions of incident and scattered light.

The first assumption allows the single-scattering approximation to be imposed.This can be satisfied by controlling the density of the medium during measurements.If the medium is optically thin,the density of particles in the medium is low,so theprobability of scattering is low and single scattering can be assumed.From the second assumption,angleθ between the scattered light and the ray axis ž can be regarded as small,and its cosine can be approximated as

Table 1 Symbols used in equations

Fig.1 Coordinate system.

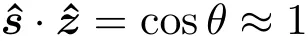
As noted in previous works[23,26],most participating media are predominantly forward-scattering,and therefore comply with this assumption.The third assumption relates to the symmetry of scattering and is commonly made in both measurements and image generation,without significant loss of generality.

The direct lightI0measured at positionr,depth z,in the direction s is given by

whereδ()denotes the Dirac delta function.Note that I0(z,r,s)≠0 wherer=0ands=0,which is along the incident light direction.The single scattering fieldI1is then calculated by a line integral along a viewing ray denoted by

Therefore,

where Ω represents a unit sphere,and the phase function p(|s-s′|)is normalized to 4π.

Let us consider the observation through an integrator. The total flux Ψ1is obtained by integrating Eq.(4)over s:

whereu=1/tandu′=|r|u.Note that the flux Ψ1depends on the distance from the axis,|r|,and is constant on a circle|r|=constant.To remove the apparent singularity from the factor 1/|r|,we integrate Ψ1over the circle and obtain:

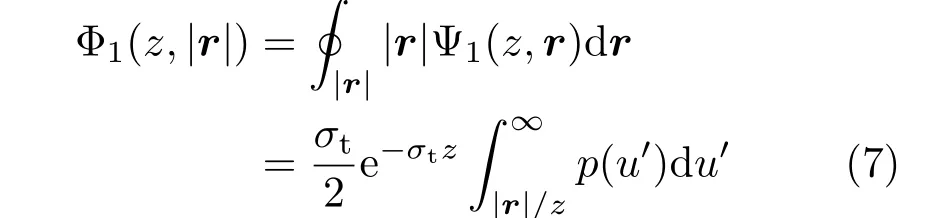
which statesthe importantfactthatΦ1is proportional to an integral of the phase function.By taking the derivative with respect to|r|on both sides,we obtain:

Note that|r|/zrepresents the scattering angle.The above equation indicates that the derivative is proportional to the scattering phase function,which is normalized to 4π.Therefore,the proportionality constant can be easily calculated.As a result,we acquire the non-parametric scattering phase function.

The flux integral expressed by Eq.(6)can be optically realized by use of a diffusing screen.Therefore,Eq.(8)suggests the following method for simple oneshot measurement of the phase function:

1) Place a diffusing screen that works as an integrator at the boundary of the medium.

2) Place a camera on the incident ray axis and capture the scattering field Ψ1.

3) Calculate the circular integral(Eq.(7))from the image.

4) Calculate its derivatives.

4 Simulation

In this section,we verify our proposed formulation through simulation.We simulate the scattering that occurs in the participating medium and create synthetic data.By applying the formulation to the synthetic data,we confirm whether a value proportional to the phase function can be acquired.In the formulation,we assume only forward scattering.We also verify the range over which the formulation is valid by simulating changes in the distribution of the phase function.

4.1 Simulation setup

Our simulation is based on the photon tracing algorithm.As shown in Fig.1,the light source emits a narrow beam entering the medium perpendicularly to the medium surface.When a photon collides with a particle in the medium,the scattering albedo determines the probability with which the photon is scattered or absorbed.When photons are scattered,the direction of propagation changes and their directions follow the phase function.For the phase function in this simulation,we use the HG function,which is represented in the form:

whereθrepresents the scattering angle andgan average cosine,which determines the distribution of scattering.The range ofgis-1 to 1,negative values indicating back scattering and positive values indicating forward scattering;the largerg,the greater the anisotropy of scattering becomes.When a photon goes out from either the lower or upper surface,we record its direction and position.We apply the formulation given in Section 3 to the recorded photon.We then evaluate the derivative.To confirm that the derivativeisproportionaltothephasefunction,weperform fitting between the derivative and the HG function:

whereαis a constant of proportionality. The scattering angleθis given bytan-1(r/z).The depth of the medium is 200 mm and the extinction coefficient is 1.9×10-2mm-1.We do not consider absorption and hence the scattering coefficient is equal to the extinction coefficient.

4.2 Simulation resu lt

Fig.2 Simulation result.Red line:HG function.Blue line:derivative of Φ1.

The simulation result is shown in Fig.2.Wheng is equal to 0.7 or higher,the derivative of Φ1and the HG function coincide.Thus,our theory holds for forward scattering.However,whengis equal to 0.5 or less,our formulation does not work as well and the derivative of Φ1and the HG function do not match.In conclusion,when the scattering phase function corresponds to strong forward scattering,withg≥0.7,our formulation can be applied and works well.

5 Experiments

In this section,we describe the experimental setup that we devised based on the formulation proposed for measuring the non-parametric phase function of real media.

5.1 Experimental setup

Fig.3 Experimental setup.

Figure 3 presents a schematic diagram and a photograph of the experimental setup. In the formulation,the incident ray is considered to be a narrow beam.To ensure this requirement,we used an LED projector(Optoma ML750)and two pinholes of the same size(0.4 mm).We set up the projector to direct a beam of white light through both pinholes and mounted them over a water tank ensuring that the beam was incident normal to the surface of the participating medium.A diffuse screen was placed under the tank to integrate the flux of scattered light.A DSLR camera(NIKON D5300)was placed under the screen to image the scattered light.In total,our method requires only a projector,a camera,a diffuse screen,a tank,two pinholes,and holders for each of them.Preparing the setup is very easy compared to setups used in previous studies measuring the nonparametric scattering phase function.

We confirmed that the setup functioned correctly by testing several media(milk,apple juice,and Chardonnay wine)representing different types of characteristics(optically dense and optically sparse).To comply with the assumption that single scattering is dominant,the medium was diluted with water.The diluted medium was poured into the tank to a depth of 50 mm.

5.2 Extracting non-parametric scattering phase function

The work flow to obtain non-parametric scattering phase function is shown in Fig.4.Firstly,using the above setup(Fig.3),the scattering field(a)is acquired as a captured image which represents the distribution of the scattering effect.The scattering field is expressed in polar coordinates Ψ1(r,θ).Then,we calculate the circular integrals Φ1of the scattering field Ψ1(r,θ)on circles of varying radiusr.According to Eq.(8),the scattering phase function is proportional to the derivative ∂Φ1/∂r,which we now compute.Note that the scaling factor can be determined by assuming that the total phase function is normalized by 4π.

Fig.4 Work flow for measuring the non-parametric phase function.Illustration of(a)observation from lower angle,(b)obtained scattering distribution,(c)Φ1,and(d)Ψ1which is proportional to the scattering function.

5.3 Experimental results

Experimental results are presented for different media in Fig.5(milk),Fig.6(apple juice),and Fig.7(wine).The scattered light spreads out around the incident beam.Each scattering field has a different distribution.We calculated the phase function in each case.

In calculating the phase function,the RGB color channels of the captured image are independently used for calculating the phase function.The measured phase functions are different for each medium;the differences arising from the color for one medium are relatively small but still cannot be ignored.While all indicate strong forward scattering,the shape of the phase function is different for each medium.Indeed,we acquired different types of phase function.

The acquired phase function has unnatural features such as the second and third peaks.Such peaks seem reasonable as the characteristics of Mie scattering;however,they could also be artifacts caused by the setup such as diffraction at the pinholes.Validations of correctness remain as future work.

Fig.5 Experimental result for milk.(a)Scattering field captured through screen at bottom.(b)Pseudo-color of captured scattering field.(c)Measured phase function versus scattering angle.(d)Polar plot of phase function.The incident direction is from left to right and intensity is given on a log scale.

Fig.6 Experimental result for apple juice.(a)Scattering field captured through screen at bottom.(b)Pseudo-color of captured scattering field.(c)Measured phase function versus scattering angle.(d)Polar plot of phase function.The incident direction is from left to right and intensity is given on a log scale.

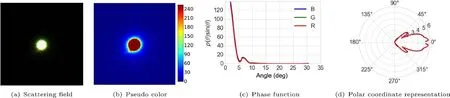
Fig.7 Experimental result for wine.(a)Scattering field captured through screen at bottom.(b)Pseudo-color of captured scattering field.(c)Measured phase function versus scattering angle.(d)Polar plot of phase function.The incident direction is from left to right and intensity is given on a log scale.

The major limitation inherent in our method is that,as with other methods,it is difficult to measure the phase function at scattering angles≈0.In real settings,direct light is much stronger than scattered light.Therefore,the light scattered at small angles cannot be measured.

5.4 Rendering

Figure 8 presents rendered images of the measured media(milk,apple juice,and wine)in a glass.We used a physics-based path tracing algorithm for rendering.The image size is 1024×1024 pixels,and we traced 20,000 ray samples for each pixel.Rendering used the measured non-parametric phase function as tabulated data.The scattering and extinction coefficients were manually determined.Furthermore,because we cannot measure all directions,we filled in missing values of the phase function to allow complete rendering.

6 Conclusions

We have proposed a method that acquires the nonparametric phase function from a single image.Our setup for the measurement requires neither special equipment nor complicated calibration.Also,we have presented rendered images of several different media using measured phase functions.Our proposed model still has a few limitations.Because we ignored the effect of higher-order scattering,we diluted the media to decrease the scattering of light.We also assumed that the scattering distribution is concentrated in the forward direction so that the part of the phase function corresponding to back scattering need not be measured.While we can now measure the phase functions of a wide range of media,in rendering the image,it is necessary nevertheless to measure other scattering characteristics such as the coefficients of extinction and scattering. Our scattering model presumes these coefficients are known,to allow rendering of the measured materials.The ultimate objective,which remains as an open problem,is to measure the scattering properties of a wide range of media and to summarize them all in a single data set.

Fig.8 Rendered images using a physics-based path tracing algorithm.Scattering parameters were manually determined.Left:milk,σt=(0.21,0.21,0.21),σs=(0.16,0.15,0.15).Center:apple juice,σt=(0.016,0.027,0.015),σs=(0.013,0.015,0.041).Right:wine,σt=(0.015,0.027,0.076),σs=(0.015,0.021,0.041).Units:mm-1.Gamma curves and exposures of all images were adjusted for clarity.

Appendix A Derivation of formulae

For completeness of this paper,we present in detail the derivation of formulae given in Section 3.The single scattering fieldI1,Eq.(4),is calculated by a line integral along a viewing ray:

The total flux Ψ1,Eq.(6),is obtained by integrating Eq.(4)over s:

Acknowledgements

This work was partly supported by JSPS KAKENHI JP15K16027,JP26700013,and JP15H005918.