Deforming generalized cylinders without self-intersection by means of a parametric center curve

Ruibin Ma(),Qingyu Zhao,Rui Wang,James Damon,Julian Rosenman3,,and Stephen Pizer,3

Abstract Large-scale deformations of a tubular object,or generalized cylinder,are often defined by a target shape for its center curve,typically using a parametric target curve.This task is non-trivial for free-form deformations or direct manipulation methods because it is hard to manually control the centerline by adjusting control points.Most skeleton-based methods are no better,again due to the small number of manually adjusted control points.In this paper,we propose a method to deform a generalized cylinder based on its skeleton composed of a centerline and orthogonal cross sections. Although we are not the first to use such a skeleton,we propose a novel skeletonization method that tries to minimize the number of intersections between neighboring cross sections by means of a relative curvature condition to detect intersections.The mesh deformation is first defined geometrically by deforming the centerline and mapping the cross sections.Rotation minimizing frames are used during mapping to control twisting.Secondly,given displacements on the cross sections,the deformation is decomposed into finely subdivided regions.We limit distortion at these vertices by minimizing an elastic thin shell bending energy,in linear time.Our method can handle complicated generalized cylinders such as the human colon.

Keywords generalized cylinder;deformation;skeleton;self-intersection

1 Introduction

The generalized cylinder(GC),or quasi-tube,is a widely used model in computer graphics[1].The mathematical definition of a GC consists of a centerline(or medial axis,skeletal curve,etc.)and a set of orthogonal cross sections(CS)[2].Accordingly,3D models of GCs can be constructed by spline-based methods[3—6].In this paper,however,we consider a discretized representation for GCs,i.e.,a triangle mesh(usually of high resolution),which is a more typical representation in computer graphics.

Deformation of GCs is a common and important problem in computer graphics:see Fig.1.Compared with free-form deformation[7]that uses enveloping control points,direct manipulation[8]can be more intuitive,as the user moves control vertices on the surface.Thus,several large-mesh deformation methods have been proposed using direct manipulation[9—17].Furthermore,skeleton-based methods,or skinning methods[18,19],have the advantage of imposing prior knowledge,via efficient control of the object's skeleton.Joints and edges are commonly adopted to deform 3D character meshes[20].Such skeletons are either manually given[21]or computed by methods based on the Voronoi diagram[22]or harmonic skeleton[23].

Fig.1 Centerline-guided generalized cylinder deformation. A generalized cylinder is deformed in large scale while maintaining its local curvature patterns.

In this paper,however,we focus on the common practice of driving GC deformation by the shape of its centerline.We consider GCs with a clear tubular structure(so essentially one outstanding dimension).The centerline of a GC is densely sampled and represented as a parametric spatial curve which can be deformed into a new target shape.In this situation,deforming GCs via direct manipulation becomes challenging,especially for highly curved centerlines because it is difficult to manually impose accurate control of the centerline curvature.This difficulty also arises for cage-based free-form deformation or skeleton-driven approaches that use very sparse skeletal control points.

Closely following the mathematical definition of a GC[2],we use a centerline and discrete profile CSs as the skeleton.Skeletonization methods have been proposed to extract centerlines[24],CSs[25],or both[26]. However,none of these methods considered how to prevent surface folding resulting from intersections between the extracted CSs.To address this problem,our proposed approach extracts CSs and tries to minimize their intersections before deformation. A tentative centerline is extracted[24]and modified based on a relative curvature condition[27]that detects intersection.The modified centerline and its respective CSs are then used as the canonical skeleton for the subsequent deformation.Given the target centerline as a parametric 3D curve,all orthogonal CSs are mapped using rotation minimizing frames[28].Next,because our densely sampled centerline and CSs divide the mesh into small regions,the displacements in each region can be determined efficiently by minimizing a quadratic thin shell bending energy[29,30],using the displacements on the CSs as constraints. The output of our algorithm is a GC whose geometry follows the target centerline shape while preserving local curvature patterns.

Our main contributions include:(i)a skeletonization method based on a relative curvature condition that minimizes intersections between CSs,enabling large-scale geometrical deformation,(ii)efficient determination of fine-scale(vertex-wise)deformations based on a thin shellmodelthatusesthe displacements on the CSs(the results of geometrical deformation)as constraints,and(iii)a strategy to control twisting using rotation minimizing frames.In the first contribution,our method does not guarantee to exclude all CS intersections,but tries to minimize them.

This paper is an extended version of a previous short paper[31].In Section 2 we review methods of skeleton-driven deformation and skeletonization especially relevant to GCs.In Section 3 we brie fly introduce the algorithm pipeline.Details of skeleton extraction,and deformation of the skeleton and boundary mesh are introduced in Sections 4 and 5 respectively.Section 6 shows deformation results for a variety of GCs.We show shape morphing for several objects whose centerline parameters are continually changing,and in particular,we show an example application of colon visualization.Finally,in Section 7,we summarise our findings and consider limitations and future work.

2 Related work

2.1 Skeleton-driven deformation

Yoshizawa et al.[22,32]used a Voronoi-based medial surface as the skeleton and performed freeform deformation on it. Kho and Garland[21]used a reference curve to drive mesh deformation.Shi et al.[33]proposed a mesh puppetry method that uses high-level user-defined constraints in conjunction with sparse control-point-like skeletons.In Ref.[18],Kavan et al.used dual quaternions to eliminate artifacts arising in standard skeletal subspace deformations.Example-based deformations,like pose space deformation[34]and context-aware skeleton shape deformation[35],took advantage of known shape examples to make more reasonable interpolations.Wei and Rossignac[36]proposed a spine-driven method to preserve volume while deforming a mesh.The work by Angelidis and Singh[37]preserves volume and prevents foldings using kinodynamic skinning.Rohmer et al.[20]expanded the idea to local sub-volume preservation and also prevented foldings.Kavan and Sorkine[19]used elastic models.Vaillant et al.[38]proposed a geometrical post-processing method to deal with skin contact.Their methods are close to ours in motivation,but they did not consider how to extract the skeleton,especially for structures like a human colon that have highly curved sections.

2.2 Skeletonization

Verroust and Lazarus[39]extracted skeletal curves from a point cloud by connecting centroids of level sets computed from a neighborhood graph.Mortara and Patan`e[40] first detected high curvature regions and computed topological rings by growing spherical bubbles from each region;the skeleton was computed by connecting the centroids of the rings.Chuang et al.[41]proposed a potential- field-based skeletonization method.Their method produces small branches to capture small local geometric details such as corners.Aujay et al.[23]proposed use of anatomic information to extract skeletons,based on a harmonic function which captures joints of characters more realistically.The method proposed by Antiga et al.[24,42,43] finds a centerline on the Voronoi diagram of the triangle mesh by maximizing distance to the boundary.Their method has more similar goals to our work but still does not minimize intersections between CSs.

2.3 Centerline and cross sections

Wang et al.[44]proposed a soft-straightening method using a centerline and CSs. They prevented intersection of CSs by simulating electrical charges on the centerline and used deflected electrical force lines to sample the CSs. The CSs are stacked to form the straightened surface. However,two problems remained unsolved in their work: firstly,how to geometrically prevent intersections,i.e.,how to have a centerline and strictly planar CSs while minimizing intersections,and secondly,based on the deformation of the skeleton,how to compute a point-wise displacement field without sampling or interpolation,in such a way as to maintain local curvature patterns on the surface. The work of Zhang et al.[17]combined the skeleton(a centerline and CSs)with the “as-rigid-as-possible” method[14].They showed the approximately-volume-preserving benefit of utilizing the skeleton,but their initial centerline shape is restricted to being straight and thus is inapplicable to long tubular meshes of the kind we consider.In Ref.[25],level-sets computed by conformal mapping provide an alternative to CSs,but these contours are not planar and there is no centerline associated with them as a basis for skeletal manipulation.

3 Algorithm pipeline

For an input triangle mesh representing a GC,our method outputs a mesh whose centerline follows a pre-specified target geometry such as a straight line or some other 3D parametric curve.Specifically,the method produces a vertex-wise mapping.See Fig.2.To compute this mapping,we use a discrete skeleton to perform the deformation.We densely and uniformly sample discrete points on a centerline,and we compute a CS at each point.The whole process thus comprises a skeleton extraction step and a deformation step.

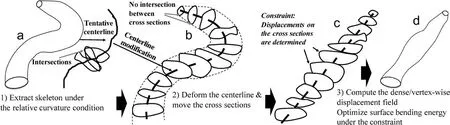
Fig.2 Pipeline of skeleton-based GC deformation with relative curvature preservation.Input:a GC,and a target centerline shape.Output:a deformed version of the GC.

In the skeleton extraction step,we find a centerline for which the discrete CSs do not intersect by incorporating a relative curvature condition.In the deformation step,we reshape the centerline to the target parametric shape. The cross sections are then mapped accordingly using rotation minimizing frames.Under the constraint that the displacements on the CSs are determined and fixed,we solve for the displacements of all the other inter-cross-sectional regions by minimizing thin shell bending energy.

4 Skeleton extraction

4.1 Mathematics of generalized cylinders

A generalized cylinder(GC),as defined in Ref.[2],is“a solid whose axis is a 3D space curve and at any point on the axis a closed cross section is defined”.Usually the cross sections are restricted to be normal to the axis,or centerline;this is a space curve:c(s)=(x(s),y(s),z(s)).In Ref.[24],it is defined as a curve inside the GC that maximizes the distance from the boundary.We define a cross section(CS)at a centerline point to be the intersection between the surface and the plane orthogonal to the centerline at that point.If the intersection has multiple connected components,the profile of the one closest to the centerline point is taken as the CS.Two CSs intersect when their planes intersect within the two connected components bounded by the two CSs.During deformation,we impose a constraint on the skeleton that is further used to modify the centerline(see Section 4.3):the CSs should not intersect.

At each point on the centerline,a frame can be defined locally:(t,u,v).For example,a well-known choice is the Frenet frame(tangent,normal,binormal). In this frame,the(u,v)plane is orthogonal to the curve.

4.2 Initial centerline and cross sections

As noted in Section 4.1,the method in Ref.[24]minimizes the following energy by finding a path between two user-given points p0 and p1:

where Fis a function which has smaller values for more internal positions(see Ref.[24]).The function is minimized on the Voronoi diagram of the GC mesh[24,42,43].

We adopt this method to extract a tentative centerlinectlinitialthat is represented as a series of discrete points. Points onctlinitialare uniformly sampled. At each point,we compute a CS as explained in Section 4.1;it is explicitly represented by a set of discrete points and edges.An important property we want the skeleton to have is for there to be no intersections between CSs,which may be violated when centerline curvatures are high,as shown in Fig.3(left).

4.3 Centerline modification based on the relative curvature condition

The CSs ofctlinitialcannot be used as the skeleton because cross-sectional intersections lead to surface folding:see Fig.4.In Ref.[27],Damon presented a relative curvature condition(RCC)for non-singularity of a generalized cylinder;it can be used to detect crosssectional intersections in the continuous situation.Accordingly,an algorithm based on this condition,and smoothing,is performed onctlinitialto avoid intersection.The algorithm and its mathematical basis are now explained.

The relative curvature condition is illustrated in Fig.5.A cross section is locally orthogonal to the centerline.The(Frenet)normal direction lies in this orthogonal plane.Each point on the cross section can be represented by a vector based at the corresponding centerline point.We represent the angle between the vector and the normal direction byθand the length of the vector byr.For a non-intersecting cross section,all boundary points must satisfy:

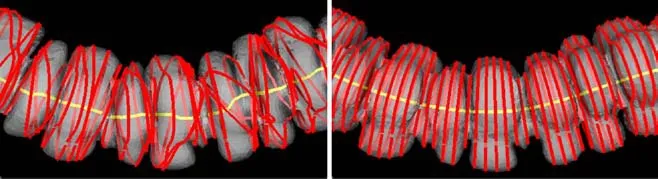
Fig.3 Yellow curve:centerline.Red curves:cross sections.The GC surface is a human colon segmented from CT.Left:centerline computed by Refs.[24,42,43],with large and discontinuous curvatures,leading to intersections.Right:centerline modified according to the relative curvature condition,without intersections between cross sections.

Fig.4 Self-intersections between cross sections result in surface self-intersections.(a)Straight tube before bending;(b)tube bent using intersecting cross sections;(c)tube bent using non-intersecting cross sections.

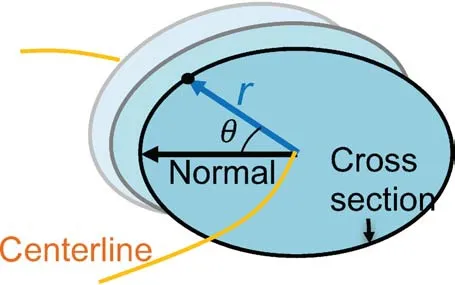
Fig.5 Relative curvature condition.

whereκ(s)is the local curvature of the centerline.The relative curvature condition only constrains the points on the side of the normal withcos(θ)＞ 0.The term κ(s)cos(θ)is the so-called relative curvature.The condition suggests that regions with larger relative curvatures should have smaller radii,which is consistent with intuition.The relative curvature condition detects intersections between CSs in the continuous situation.If each point on all CSs satis fies this condition,no CS will intersect any other CS.

In our discretized implementation,each CS is represented by a number of points,and we only deal with those points.We require the inequality condition to hold for all points on the CSs,but it may be violated for regions ofctlinitialwith large centerline curvatures.We thus modifyctlinitialby smoothing:see Algorithm 1.The CSs are updated based on the modified centerline ctlmodified.

Algorithm 1 has two stages.We first perform iterative Gaussian smoothing and centerline adjustment according to local curvatures,trying to satisfy the relative curvature condition for each CS.Secondly,for CSs with large radii for which it is difficult to satisfy the relative curvature condition,we perform interpolation between neighboring satisfactory crosssectional planes to compute the CS:see Fig.6.Interpolation ensures uniform change of orientations of the interpolated planes.It is done in a Lorentzian metric space[45]. Orthogonality can be slightly relaxed for the interpolated planes; this nonorthogonality is preserved during the mapping procedure in Section 5.1.Details can be found in the pseudo-code.The resulting skeleton can be regarded as a swept procedure along the centerline.Although orthogonality is relaxed in some parts of the centerline,the normal and interpolated planes can be together regarded as a continuous Lorentzian vector if eld.

?

The resulting skeleton and its associated CSs have no intersections.ctlmodifiedmust then be deformed.The right-hand side of of Fig.3 shows an example ofctlmodifiedand the non-intersecting CSs computed from real data(a human colon).

Fig.6 Replacing intersecting CSs with interpolated ones.

5 Deformation

The deformation step consistsofa skeleton(geometrical)deformation step(see Section 5.1)and fine-scale thin shell deformations in subdivided regions(see Section 5.2).The skeleton deformation step deformsthe centerline into the desired parametric curve.Relative rotation between CSs is controllable;if no artificial twisting is desired,we minimize relative rotation between CSs using rotation minimizing frames[28]. The mesh deformation step takes the deformation of the skeleton as input and computes vertex-wise displacement vectors by minimizing bending energy.

5.1 Skeleton deformation

We design the surface deformation by specifying how the centerline and the position of each CS change.Because we only consider shape change for the centerline,the shapes of the cross-sectional curves remain unchanged during the process.They move along with the centerline.

5.1.1 Detail

1.ctlmodifiedis taken to be a discrete curve with each point assigned a location with respect to to arc length.The target centerline is a parametric space curve sampled uniformly using the same number of points as ctlmodified.

2.At each point onctlmodified,we compute a rotation minimizing frame(denoted by RMF).Its tangent direction is constrained to be the tangent to the centerline. The other two directions are orthogonal.Rotations between neighboring frames are minimized following[28].

3.The target centerline is defined as a parametric curve and is sampled uniformly using the same number of points asctlmodified.The total length of the curve(point spacing)can change if stretching is desired.

4.At each point on the target centerline,we construct a new frame(denoted by NEWF)whose tangent direction is also the centerline tangent. The other two orthogonal directions are set according to user-defined consistency.For example,in a straightening task,no twisting(see Fig.7(b))is desired,resulting in all NEWFs in the same direction. If twisting is wanted,the twisting amounts can be parameterized(see Fig.7(c)).

5.Finally,we map(via a rigid transform)each CS according to its RMF and NEWF.(Any slight non-orthogonality in Algorithm 1 is preserved.)

A parametric curve provides a powerful way to form shapes that can not be easily achieved by direct manipulation,such as a helix with chosen radius and vertical spacing.It allows continuous shape variations of the GC with shape parameters gradually changing or moving along a path in a shape space.We can perform all kinds of manipulation on the centerline as long as the CSs preserve their local positions relative to the centerline and the relative curvature condition is not violated.For example,the three schemes in Fig.7 show manipulations of straightening,twisting,and bending.

5.1.2 Why not use the Frenet frame?

The Frenet frame comprises the local tangent direction of the curve,its normal direction,and the binormal direction.The normal is in the derivative direction of the tangent,and the binormal is in the derivative direction of the normal.In comparison,rotation minimizing frames also use the tangent direction,but the two other orthogonal directions are computed consecutively from end to end so that the rotation between any two neighboring frames is minimal.

Although normal directions are used in the relative curvature condition,we do not use Frenet frames in step 2.Because of twisting caused by torsion of the centerline[6],it is hard to maintain or adjust relative orientation of neighboring CSs during deformation.Orientation consistency between NEWFs becomes intuitive for users if the source frames already have minimal rotation between each other.For example,in Fig.7(b),to straighten a GC without twisting,we can simply set each pair of adjacent frames to be identical so that they also have minimum rotation between each other.It is hard to determine appropriate orientations needed to produce Fig.7(b)if the orientations in Fig.7(a)are not rotation minimizing frames.

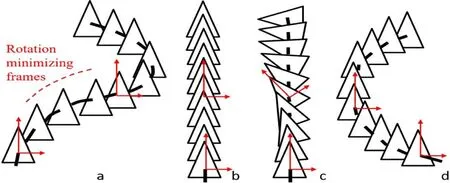
Fig.7 Three examples showing the process of deforming the centerline and moving the CSs.(a)A centerline&CSs computed using the relative curvature condition.There is no intersection between cross-sectional curves inside the GC.For each CS,two directions are calculated using rotation minimizing frames.(b)Target centerline shape:straight,without twisting.(c)Target centerline shape:straight,with artificial twisting.(d)Target centerline shape:semicircle.

Notice that our skeleton approach is compatible with traditional free-form deformation.Using control points,the centerline can be easily modeled as a spline for use in our current skeleton deformation scheme.If the centerline is bent too much and the relative curvature condition is violated,self-intersection can occur,in which case we prohibit that deformation.While our method cannot handle such a case,it can identify when and where problematic bending occurs.

5.2 Mesh deformation

Skeletal deformation implies underlying surface deformation. Our final objective is to compute the deformation of the whole surface:the result should be in the form of displacement vectors of each vertex on the surface. The deformation of the centerline precisely gives the displacements on the cross-sectional curves.Because these curves are calculated by intersecting the surface with planes,they do not necessarily pass through any vertex on the surface,so instead we first determine the displacements of vertices that are close to the CSs(we use a distance threshold∈=0.1× the centerline point spacing)and also satisfy the relative curvature condition.These vertices are then mapped by the method in Section 5.2.1.

After fixing the displacements of the vertices close to CSs,the remaining problem becomes:given the constraint of the fixed displacements of a subgroup of vertices(Vfixed), find the displacements for all other vertices(Vunknown)on the surface such that local curvature patterns are preserved.We solve this problem by minimizing a bending energy defined on the triangle mesh under the constraint that the displacement of Vfixedremains unchanged.

5.2.1 Constraint: fixed displacements

The set of verticesVfixedis selected as those whose distance to any cross-sectional curve is smaller than a threshold and also satisfying the relative curvature condition. For each of such vertex,we can find its positional parameter(s)along the centerline by finding its closest point on the interpolated polynomial curve of the centerline between the two bounding CSs.Givens,we can compute the local rotation minimizing frame RMF(s)and the target new frame NEWF(s),allowing this vertex to be mapped accordingly.

We do this only for theVfixedvertices for two reasons.Firstly,not all vertices satisfy the relative curvature condition in practice,especially those outside an∈-neighborhood of the CSs,but we still desire to find their displacements under the constraint that the displacements of the others are optimum in the sense of a bending energy(see next section).Secondly,the two bounding CSs for the other vertices can be hard to determine.Without this information,thesparameter can be ambiguous because a vertex's closest point on the whole centerline may not be the correct corresponding centerline point.This is especially common for surfaces with great local geometric detail,or so-called topological noise[46—48]like small handles.

5.2.2 Minimizing surface bending energy

The displacements of the verticesVunknownare calculated by minimizing the thin shell bending energy[29,30,49,50],which can be approximated as the squared Laplacian[29,30]of the displacement function defined on the mesh,(Δf)2.It essentially characterizes the change of mean curvature in a local surface patch,which serves as a proxy for measuring local elastic bending of the structure(considered as a thin shell).This requires the definition of a discrete Laplace—Beltrami operator on the triangle mesh[51,52]:

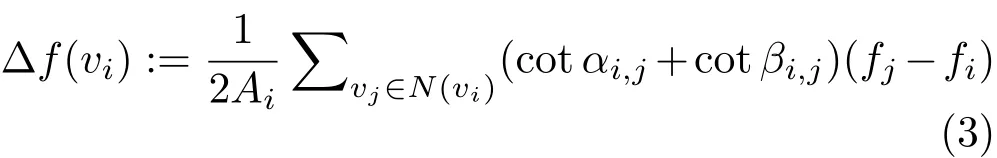
In this equation,fis any function defined on the mesh,vstands for the vertices on the mesh,andα andβstand for the two opposing angles in the two triangles that share edge(i,j).Airepresents the area of the mixed Voronoi cell[51]of vertexvi.N(vi)is the set of neighbors of vertex vi.

In practice,as our centerline is densely sampled(with up to 1000 sample points for long tubes like colons),the mesh is divided byVfixedinto many small regions.For each of these regions,the boundary is composed of certain vertices inVfixedwhose displacements are fixed. These boundary displacements provide a constraint when solving for the unknown displacements inside this region.We initialize the displacements ofVunknownwith a rigid transformation,a global transformation that does not produce a local elastic bending energy and thus does not affect the final optimization.This rigid transformation is initialized to best fit the fixed displacements forVfixedin terms of summed squared error.The process is now explained in detail.

In the following,we denote vertices/regions in their original positions using the subscripto,those rigidly transformed by the subscriptr,and in the target byt.Formally,letRobe a region composed ofandon the original mesh.are the target positions of.Tis the rigid transformation defined byandsuch that the sum of squared distances betweenandis minimised.The vertices after transformation are denoted byand,respectively:

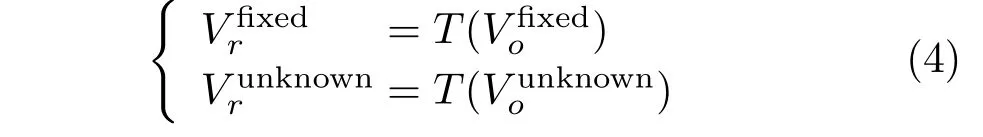
Let the transformed region be.Our target is to computeRt,composed ofand.Letfbe the displacement function from RotoRtandgbe the displacement function fromRrtoRt.Again,part ofgis known as.Assumingand,the thin shell bending energy of g is

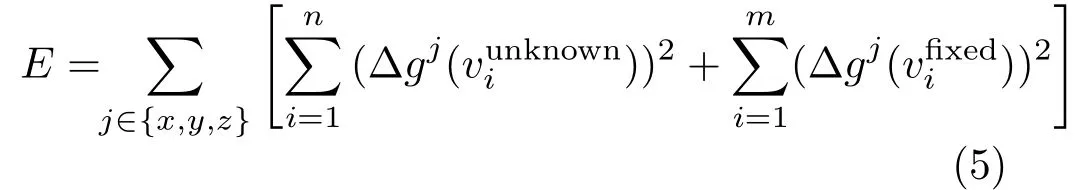
Note the integral domain includes the fixed vertices because the Laplace—Beltrami operator may involve their neighboring vertices whose displacements are unknown.This energy can be cast into a quadratic form and minimised efficiently.

Finally,havingg,we can solve forffor:

We do this for each region separately. As a result,we get a displacement vector for each vertex.Theoretically,this linear solution does not guarantee a non-intersecting solution.However,as our method decomposes the overall large deformation into many small inter-cross-sectional deformations using relatively dense CSs,and the geometry of each piece of sub-surface is quite simple,we have not encountered intersection in practice.

6 Results

Depending on the complexity of the input meshes,the number of cross sections used varies from 200 to 400.Computation time varies from 15 to 60 s using a single thread on an Intel i7 CPU.The most timeconsuming step is calculating cross sections,which is readily parallelizable.

In Section 6.1 we show examples of deformation of five meshes as a proof-of-concept.In Section 6.2 we show an example to illustrate the ability to deal with high curvature regions and local geometrical details.In Section 6.3 we show examples of shape variations controlled by skeletons whose parameters are continuously changing.In Section 6.4 we show an application of our method to human colon visualization.In Section 6.5,we show a failure case.

6.1 Deformation examples

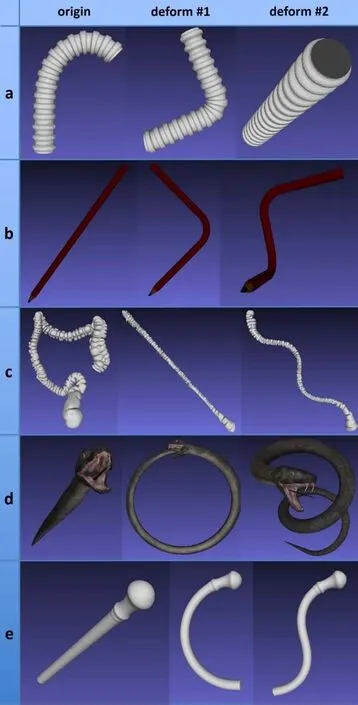
Fig.8 Five examples of GC deformation.Left:original GC.Middle,right:deformed shapes;the target centerline shapes are parametric curves.(a)Flexible tube,(b)pencil,(c)human colon,(d)snake,(e)cane.

As a proof-of-concept(see Fig.8),we demonstrate our method on five generalized cylindrical objects:a lf exible tube,a pencil,a human colon,a snake,and a cane.For each object,we show two deformation results with different target centerline shapes given as parametric space curves.Our geometrical(skeleton)deformation efficiently deformed the objects on a large scale to the target centerline shape,giving precise control of the centerline curvature.Crosssectional intersection was avoided in these examples.Additionally,thanks to the use of the thin shell model,our method does not introduce unnecessary distortion,and local curvature patterns are preserved.

6.2 High curvature regions

Figures 9 and 10 show two parts of a colon with high curvature.While straightening the colon,allowing visualization of its interior at-a-glance(see Section 6.4),our method prevents skeleton-level intersection and keeps local curvature patterns.Moreover,our method does not need to treat so-called topological noise[46,47]or small handles as special cases.

6.3 Parametric mesh morphing

A parametric curve is an efficient tool to guide the deformation of a generalized cylinder because the target skeleton is inherently consistent with the skeleton of a generalized cylinder.Moreover,defining the target mathematically enables us to control the centerline curvature precisely,which can be hard for direct manipulation methods.To address this point,we show some examples whose shapes are morphed according to underlying skeleton parameters.Figure 11 shows shape variations of a snake whose centerline is bent into a helix whose parameter is continually changing.Figure 12 shows shape variations of a colon mesh whose centerline is parameterized as a sine curve of varying frequency.In Section 5.1 we mentioned the ability to control twisting:this is illustrated in Fig.13.The orienta-tions of the new frames on the target curve are parameterized.In these examples the target curve is of the same length as thectlmodified.However,we can change the spacing of the points on the target curve,as shown in Fig.14 where we stretch a flexible tube to different lengths.

Fig.9 Deformation(left to right)of a human colon.The blue disks show corresponding positions of a high curvature region.Crosssectional intersections are prevented,and local curvature patterns are preserved.

Fig.10 Multiple components.The red arrows indicate two small handles.Our method is robust to topological noise.In this situation there may be locally more than one connected component in the cross-sectional plane.We keep the one closest to the centerline as the cross section in practice.

Fig.11 A snake deformed into helices with different parameters.The densely-sampled centerline lies precisely on a mathematical helix.It is easy to impose precise curvature control using our method.

Fig.12 The centerline of a colon mesh following sine curves of different frequencies.

6.4 Colon visualization

Fig.13 Twisting.(a)A cuboid mesh.(b)-(d)Twisting is applied to the cuboid.The resulting mesh changes as the twisting degree is increased.Although the points on the centerline stay static in this example,the relative rotations of the cross sections changes.

Fig.14 A flexible tube stretched to different lengths.This is done by changing the point spacing on the target parametric curve.

Our method is applicable to colon visualization.Colon visualization has been an important research area in medical image analysis.Due to the highlycurved nature of the colon's surface,it is very difficult for physicians to examine the complete surface of a colon during colonoscopy or using virtual colonoscopy based on modalities like CT.Therefore,unfolding approaches have been proposed to help physicians view a colon at-a-glance.One popular category of unfolding methods is conformal mapping[25,46,47,53—57].Conformal mapping maps a surface of tubular topology to a plane.The resulting 2D surface is colored by curvature information or volume rendering intensities.However,traditional conformal mapping eliminates 3D geometry and only keeps it as intensities.As noted in Refs.[54,55],this can hide important diagnostic information;there have been efforts to improve conformal mapping by preserving more geometric context.Based on conformal mapping,Nadeem et al.[54]proposed a shape-preserving mapping that enlarges the examined surface area in virtual colonoscopy,by conformal deformation of local regions of interest. Their resulting mesh is still tubular in 3D,and is applicable to any arbitrary genus surface and topology.Wang et al.[55]also proposed so-called 2.5D mapping by assigning heights to planar pixels by computing distances to local fitted cylinders.Marino et al.[56,57]proposed a context-preserving mapping that maps a tubular surface to a plane according to its projected 2D skeleton.This approach keeps very high-level geometry context for a tubular or treestructured object like a skeleton in order to stretch the generalized cylinder.

As an alternative to conformal mapping approaches,we have applied our method on colon visualization.The colon surface is first straightened while keeping its tubular structure and local curvature patterns.Straightening is one of the simplest applications of our method.The straightened colon is then slit open longitudinally.We then simply map the quasitube from a cylinder to a semi-cylinder,allowing the interior of the colon surface to be displayed succinctly.This process is shown in Figs.15(a)—15(c).A rectangle produced by conformal mapping[53]is shown in Fig.15(d).

Compared with conformal mapping,our method has the following three advantages: firstly,the area distortion is considerably less in our method.Our method uses geometrical deformation as the constraint,keeping the shapes of the cross sections and also the length of the centerline.Local curvature patterns are preserved by minimizing the thin shell bending energy.This guarantees that no unnecessary distortion is introduced in addition to the target deformation.Secondly,our method keeps geometric context in 3D rather than flattening the surface.The surface can be colored with additional texture such as the texture extracted from colonoscopic videos[30](illustrated in Fig.16 with a synthetic texture).This idea is similar to the approaches in Refs.[54,55],but our method has a more explicit geometric constraint.Thirdly,our method does not need special processing of topological noise[56,57].We illustrate these advantages in Figs.15—17.Figure 17 compares our semi- flattening with conformal flattening of a colon section.The four pictures on the right are four slightly different views(rolled back and forth,left and right).Keeping local geometry makes the visualization more intuitive because it is in 3D.

Fig.15 Visualization results.(a)Original colon mesh.(b)Colon straightened by our method.(c)Slit-open colon.(d)Conformal flattening colored with Fiedler information[53].

Fig.16 Visualization of the interior of a straightened colon.Geometry and synthesized texture are displayed together.

Fig.17 Above left:a semi- flattened colon section from the proposed method,also with top view(above center),bottom view(below center),right view(above right),and left view(below right).Below left:the same section from conformal flattening[53].

On the other hand,the advantage of conformal mapping approaches lies in their robustness.Because there is no skeletonization step,these methods do not rely on quality of the centerline and are more robust to differing mesh resolutions.The slit-open operation in our current approach is a simple cylinder to semicylinder mapping.However,a straight longitudinal slitting line may not be the best choice as it can break the geometry of haustral folds(especially through highly curved regions,or flexures).A better strategy for finding the slitting line was proposed in Ref.[53],which could be incorporated in future. Another choice of slitting line is based on the taenia coli(a longitudinal muscle along the colon),which matches colon anatomy better.

6.5 Failures

Our method fails when the target centerline bends too much(relative to the tube radius)so that the relative curvature condition is violated in the deformed skeleton even if the condition is not violated in the initial skeleton.In such a case,surface folding will happen.In the example shown in Fig.18,a human stomach mesh is bent sharply in a region with large radius.The three zoomed-in figures show how the cross sections intersect.Techniques dealing with mesh contact[22,38]could be incorporated to solve this large bending problem.Our method permits fast detection of possible intersection regions.

7 Conclusions and discussion

7.1Summary

This paper has proposed a skeleton-driven generalized cylinder deformation approach. The skeleton is composed of a centerline and its cross sections.The target is specified as a parametric space curve.Relative rotation between neighboring cross sections can also be specified.Given a triangle mesh representing a generalized cylinder,we first skeletonize it by extracting a centerline and cross sections orthogonal to it.A relative curvature condition is incorporated to avoid intersections between cross sections,to prevent surface folding.The resulting centerline is deformed into the target shape,and the cross sections are mapped using rotation minimizing frames.This geometrical deformation fixes the displacements on the cross sections that are used as constraints for the following fine-scale deformation problem.The subdivided regions are determined by minimizing a thin shell bending energy in linear time.Accurate large-scale deformation is achieved while keeping local curvature patterns.Additionally,twisting is controllable during the deformation.

Fig.18 Above:a human stomach mesh is bent through 135°which leads to surface folding.Below:close-ups of the problematic region after deformation.Cross sections:white,centerline:yellow.

Our contribution is threefold:firstly,the relative curvature condition[27]was proposed to detect singularities in polar swept surfaces in continuous situations.We are the first to apply it in a deformation problem. Our proposed skeletonization approach resists cross-sectional intersections. Secondly,we are the first to use rotation minimizing frames[28]to control twisting.Thirdly,we cast a large-scale deformation problem as a geometrical deformation and a group of fine-scale optimization problems,which can be solved efficiently.We heuristically use geometrical deformation to provide boundary conditions for a physical thin shell model.

Our method is useful when the target center curve is specified mathematically,as for visualizing the geodesic path in a shape space between two shapes for the same tubular object.Using a densely sampled centerline,our method can impose accurate control on centerline curvature.Traditional cage-based freeform deformation and direct manipulation methods are not as convenient. We have also illustrated the applicability of our method to human colon visualization,promising a good alternative to 2D conformal approaches.

7.2 Limitations and future work

Possible improvements to our method include the following:

1.Although our current method can handle quite complicated generalized cylinders such as the human colon,we lack a proof that our approach prevents intersections in all cases. When the surface deviates from a smooth generalized cylinder,e.g.,it has a protrusion on the side of the Frenet normal,it becomes more difficult to find a satisfactory centerline by smoothing.We currently use interpolation as a heuristic approach.

2.Our method is not applicable to tree-structured tubular objects.It would be useful to extend our skeleton representation to branching tubular structures like blood vessels. Xu et al.[58]proposed a method based on electrical field theory to model a branching generalized cylinder.Zhou et al.[26]proposed a generalized cylinder decomposition method which allows handling of objects composed of multiple GCs.Mortara et al.in Ref.[59]proposed a method to decompose a mesh into shape features and more specifically in Ref.[60]proposed an algorithm to decompose a mesh into tubular primitives. The special challenge in applying our method to this case,to be solved in future,is how to represent the branch point and how the cross sections come together there.

3.The centerline may lie outside the input mesh as a result of smoothing.This is why we set a maximum iteration count and use Lorentzian interpolation to deal with remaining regions that violate the relative curvature condition.Although the current method suffices for the examples shown,even for high curvature regions,a better smoothing algorithm such as the free-knot-spline method[61]could be used instead.

4.Deformations with more abundant detail and better realism have been achieved by exampledriven approaches[14,62,63]. In Ref.[62],Wampler proposed the “as-multi-rigid-as-possible”method that used spatially localized weights to blend artist-designed models.In Ref.[63],Gao et al. proposed a data-driven method that achieved smooth and complex shape morphing using very sparse control points.Our deformation strategy leverages geometric deformation in the early stage,and the shapes of cross sections are not changed,which could limit the capability for detailed deformation.While for certain objects,shape examples can be difficult to acquire,e.g.,human colon surfaces,for those with abundant shape examples,our extracted centerline could serve as an efficient geometric constraint.

5.For colon visualization,we can incorporate the method in Ref.[53]or find the taenia coli to provide a better slitting line.

Acknowledgements

We gratefully thank Dr.Saad Nadeem and Dr.Arie Kaufman from Stony Brook University and Dr.Sarah McGill from UNC Medical School for sharing their results,data,and suggestions.This work was supported by National Institutes of Health grant R01 CA158925.