FusionMLS:Highly dynamic 3D reconstruction with consumergrade RGB-D cameras

Siim Meerits(),Diego Thomas,Vincent Nozick,and Hideo Saito

Abstract Multi-view dynamic three-dimensional reconstruction has typically required the use of custom shutter-synchronized camera rigs in order to capture scenes containing rapid movements or complex topology changes.In this paper,we demonstrate that multiple unsynchronized low-cost RGB-D cameras can be used for the same purpose.To alleviate issues caused by unsynchronized shutters,we propose a novel depth frame interpolation technique that allows synchronized data capture from highly dynamic 3D scenes. To manage the resulting huge number of input depth images,we also introduce an efficient moving least squares-based volumetric reconstruction method that generates triangle meshes of the scene.Our approach does not store the reconstruction volume in memory,making it memory-efficient and scalable to large scenes.Our implementation is completely GPU based and works in real time.The results shown herein,obtained with real data,demonstrate the effectiveness of our proposed method and its advantages compared to stateof-the-art approaches.

Keywords 3D reconstruction;RGB-D cameras;motion capture;GPU

1 Introduction

Three-dimensional reconstruction has found many applications in various fields such as archaeology[1],design[2],and architecture[3].In the digitization and preservation of cultural heritage,for example,3D models of ancient artifacts can be built onsite using existing automated tools such as RGB-D SLAM that do not require experts.In contrast,for applications in mixed reality in which real data can be mixed with virtual content[4],it is still difficult to reconstruct accurate 3D models in real time when objects are moving rapidly or when the scene is large.

As the multi-view reconstruction of static scenes has matured,the research focus has shifted to multiview reconstruction of dynamic scenes containing moving objects.Such 3D reconstruction remains a challenging problem and well-studied topic in the fields of computer vision,virtual reality,and robotics.The advent of consumer-grade RGB-D cameras that can capture both depth and color information has motivated a wave of research on dynamic 3D scene reconstruction in the last few years.We may divide most existing techniques for dynamic scene reconstruction using RGB-D devices into two main categories:(a)fusion-based methods that track the motions of objects in the scene,and accumulate captured data into a canonical representation of the scene,and(b)frame-based methods that reconstruct a 3D model independently for each set of images taken at the same time.Both strategies have several advantages and limitations.

While fusion-based methods allow reconstruction of visually appealing 3D models with smooth surfaces,smooth motion,and high levels of detail,they generally fail to reconstruct fast-moving①It is difficult to quantify fast movement,but empirically we consider position change of 40 pixels or more per frame to be fast.objects.Indeed,tracking fast-moving objects is extremely difficult,and the slightest error may corrupt the canonical 3D representation of the scene. This can initiate a vicious feedback circle of tracking errors,eventually leading to completely inaccurate model reconstruction.Furthermore,using deformable models or object templates causes issues when handling large and complex scene topology changes[5—7]. Moreover,focusing only on either human reconstruction[8]or foreground objects[6,7,9—11]restricts applicability of reconstruction approaches.Most fusion-based methods use truncated signed distance field volumes for fusing depth data.This has high memory consumption,limiting the size of the scenes that can be reconstructed.Memory reduction strategies[12]exist,but they tend to considerably increase the algorithmic complexity of reconstruction.

Frame-based methods reconstruct a 3D model of the scene from a set of RGB-D camera images taken at a single moment in time;reconstruction is done independently for each frame.In contrast to fusionbased methods,as long as the input RGB-D images are well synchronized in time,there is no need to track the deformation of the constructed 3D model.This also guarantees that rapid movements can be correctly reconstructed.However,using only a single frame of data is a drawback that generally results in poorer 3D model details than from fusion-based methods.

In this paper,we follow the frame-based strategy and present a 3D reconstruction method designed to be utilized with commodity RGB-D camera hardware.Thus,in our approach,the whole 3D scene is reconstructed from scratch on each frame.This trades some loss of 3D model precision for increased resistance to topological changes. Our method does not require a template,can reconstruct scene backgrounds,and has a small memory footprint.In addition to providing real-time reconstruction,our method allows very flexible playback of recorded data.This includes synthetic 3D slow motion based on interpolation between camera frames.The technical contributions of this work are(1)a new robust and accurate time calibration method for consumer RGB-D cameras,(2)a fast depth map interpolation method to synthesize scene point clouds at arbitrary time,and(3)a real-time moving least squaresbased volumetric reconstruction method with a small memory footprint.

2 Related work

3D reconstruction research initially focused on off-line reconstruction of static scenes.Gradually the focus has shifted to dynamic scenes and achieving real-time processing speeds.In this paper,we divide related works into two main categories,fusion-based methods and frame-based methods.A comprehensive review of reconstruction algorithms can be found in Ref.[13].

2.1 Fusion-based methods

Fusion-based methods track the motions of objects in the scene over time and accumulate the captured data into a canonical representation of the scene.Following this strategy,parametric reconstruction methods display impressive results by deforming models of objects known a priori.Performance capture systems track motion by deforming a model of a human[8,14].Zollhöfer et al.[5]presented a way to scan any 3D object template,which can then be deformed in real time.The obvious drawback of fixed templates and parameterized models is their inability to deal with unexpected scene topology changes or the appearance of unknown objects in the scene.Wang et al.[15]proposed a templateless reconstruction method that can efficiently track non-rigid motions.However,the method does not work in real time and complex topology changes may not correctly be tracked.

Truncated signed distancefunction (TSDF)volumes[16]have been at the forefront of non-rigid 3D reconstruction research.TSDF volumes allow accumulation of scene details over multiple frames to achieve high-quality reconstruction,but they also require accurate tracking of object movements to avoid corrupting geometry.Newcombe et al.[6]introduced DynamicFusion,wherein depth data is accumulated into a canonical model of a scene,which is subsequently deformed using a warp field to match scene changes in real time. Innmann et al.[7]improved DynamicFusion by estimating a more dense warping field,and Guo et al.[17]made use of albedo information in motion tracking.Zhang and Xu[18]added an option to reconstruct scene backgrounds by segmenting dynamic and static content.While the reconstruction quality is high,these methods can fail when scene topology changes considerably from that of the initially estimated model.Moreover,these methods were designed to be used with a single RGBD camera.Dou et al.[10]proposed resetting the deformed model periodically to allow more extensive scene topology changes. The method relies on multiple custom-built capture devices.Follow-up work[11]has improved the reconstruction and motion estimation accuracy via machine learning techniques but retains a similar hardware setup.

2.2 Frame-based methods

Frame-based methods reconstruct a 3D model independently for each set of simultaneously-taken images.Therefore they do not require tracking of the motions of objects in the scene.Poisson surface reconstruction,proposed by Kazhdan and Hoppe[19],is a popular choice for generating high-quality 3D models from point clouds.The method considers the full structure of the scene to produce watertight meshes.An adaptation of the method for dynamic scenes together with a multi-camera capture setup was put forward by Collet et al.[9].While the reconstruction has very impressive quality,the high computational cost and custom camera setup requirement have made the method far from real-time and hard to use.Wang et al.[20]proposed another Poisson reconstruction-based system that utilizes a much simpler camera setup,but it fails under rapid motion.Alexiadis et al.[21,22]used Fourier transform-based reconstruction together with an a priori human model.The methods use consumer RGB-D devices and generate high-quality models,but they are restricted to capturing human movement.

Reconstruction methods based on moving least squares(MLS)use local fitting of point clouds to obtain a re fined set of points on surfaces.Kuster et al.[23]showed near-real-time multi-camera reconstruction by rendering MLS-processed points using point splatting. In applications,however,triangle mesh models are preferred over points.Meerits et al.[24]used a method inspired by mesh zippering[25]to generate triangle meshes for MLS surfaces.The drawback of this work is that when using many cameras,mesh density becomes unnecessarily high and the mesh joints can present some ambiguities.

3 Proposed method

The major components of our proposed system are outlined in Fig.1.We use multiple consumer-grade RGB-D devices(such as the Microsoft Kinect 2)to capture the scene to be reconstructed.Cameras are connected to small computers,termed clients.In turn,the clients are connected over a network to a single server machine.The server decompresses and buffers the received data,which is later forwarded to a GPU for reconstruction.The reconstruction process is generally divided into two parts,(1)motion estimation and(2)geometric surface estimation,ending with a visualization of the results.

We use volumetric 3D reconstruction with a hierarchical spatial structure:a volume of space to be reconstructed consists of blocks that in turn consist of voxels.This structure speeds up reconstruction as we can quickly determine whether a block contains any surfaces or not.The geometric surface is estimated using an MLS approach that assigns a signed distance function value to each voxel.A triangle mesh is extracted from the volume using the marching cubes algorithm.Finally,the reconstructed 3D model is rendered.

Fig.1 FusionMLS pipeline.

For accurate 3D reconstruction,the input images must be temporally consistent.This means that the depth maps should appear as if they were captured at exactly the same time from all cameras.Consumer RGB-D devices,however,typically lack shutter synchronization,so the captured frames are temporally inconsistent.To tackle this issue,we developed a depth interpolation scheme that generates a new temporally consistent set of images from raw RGB-D camera data.This works by(1)calibrating the clocks of all cameras so that accurate timestamps can be assigned to all captured frames,(2)estimating scene flow between each pair of consecutive depth maps for each camera separately,and(3)warping depth maps to the desired point in time using scene flow vectors.Scene flow is computed by estimating the non-rigid transformation between depth maps.

4 System setup

4.1 Hardware topology

The RGB-D devices can be placed in various configurations.When capturing small scale activity,the cameras are usually placed around objects as shown in Fig.2 to maximize view coverage.

Fig.2 Example camera setup.Four RGB-D cameras,shown with infrared images,capture a point cloud of a sample scene.The colors of the points indicate capture by different cameras.

All recent consumer-level RGB-D devices are USB connected,which imposes strict limits on cable length.By attaching a small client computer to each RGB-D camera,every client can be connected over a much moreflexible Ethernet network to a server machine,thus avoiding the constraint of RGB-D camera cable length.

The clients compress all depth maps,infrared images,and color images received from the RGBD cameras and send the data over a custom network protocol to the server.The server decompresses and buffers the images for reconstruction.Network transfers and image compression and decompression can incur variable latency.We therefore perform reconstruction at a defined point in time 500 ms after the actual time.In other words,3D reconstruction is delayed half a second to accommodate pipeline latency.

The data received from the clients can also be recorded for later playback. When using off-line reconstruction,the user is free to specify any playback speed.Because our proposed method can interpolate between frames,we can simulate slow motion playback of the scene.

All scene reconstruction takes place on the GPU to achieve highly parallel processing.At the start of reconstruction,the necessary image frames are buffered and uploaded to the GPU memory.Because the reconstruction process requires at least two consecutive camera frames from each camera,we can achieve further speedup by buffering pairs of frames on the GPU for each camera.

4.2 Time calibration

Consumer-level RGB-D cameras have timing-related drawbacks that must be addressed,including the fact that the shutters of multiple cameras cannot be synchronized and that devices lack time calibration functionality. Because we are unable to force synchronization of image capture by the RGB-D cameras,we must compensate for object movement depending on image capture time.Such motion compensation requires precise timestamps for all captured frames.This brings us to the second RGBD camera drawback:the camera clocks must be calibrated despite difficulties.

Alexiadis et al.[22]proposed solving the clock synchronization issue by recording audio using the camera's built-in microphone.The audio can then be used to align the video streams of different cameras in post-processing.We follow another route and propose an online method with high calibration accuracy that works with any RGB-D camera by assigning accurate timestamps to image frames.In the following,the reported results and constants are for the Microsoft Kinect 2 device that was used in our experiments.

The time calibration starts by setting the clocks of all computers using Network Time Protocol(NTP).As is typical for hierarchical networks,the server if rst obtains the time from a nearby stratum 2 clock and the clients in turn calibrate their clocks by querying the time from the server.Because the network adapters of all machines support hardware timestamping,we can achieve sub-microsecond clock accuracy within the local network. The time synchronization software consistently reported measured offsets below 1 µs with respect to the local timeserver.

Next,we calibrate the client computer clocks with the connected RGB-D cameras.Each camera is assumed to have a precise internal clock that starts during device initialization.Unfortunately,there is no straightforward way to synchronize this clock to computer time.The time is exposed in the data packets sent from the camera to client.These packets include a timestamp with a precision of 125µs.On the client,we record the arrival time of each USB packet from the camera.Although the USB protocol has variable speed and latency,we can correlate the device and computer clocks over a large enough sample of timestamps.

Lettcandtdbe the computer and the camera device time,respectively.We model the relation between these timers as

wheresdis the clock skew,odis the offset between the timers,andcdcis the average time between image capture and delivery of the image to the computer.We can recoversdandodusing a linear least squares regression analysis.The constantcdc,however,is dependent on the hardware and software being used.Because our capture setup consists of homogeneous hardware,we assume that this time delay is constant across devices.Hence,the relative timestamps of any captured frames remain valid.

From a sample of 3000 timestamps captured over 100 seconds,we found a significant time skewsdof-179.2±0.4 PPM(confidence level of 95%).If the time calibration is repeated after every 100 seconds,we get time uncertainty of±40 µs from skew.The timer offsetodhas a confidence interval of±23 µs.We can conclude that the Kinect 2 RGB-D camera has a reliable internal timer that can be calibrated to sub-millisecond precision.However,the calibration should be repeated periodically,for instance,every 100 seconds,to reduce the time uncertainty from clock skew estimation error.

4.3 Camera setup and calibration

Our 3D reconstruction method requires precise intrinsic and extrinsic camera calibration.

Time-of- flight-based RGB-D cameras such as the Kinect 2 typically have one depth sensor and one color imaging sensor at different viewpoints.Intrinsic parameters for both are calibrated in-factory and are readable from the device.Extrinsic parameters for converting coordinates between sensors are also typically available. In the case of the Kinect 2,the extrinsic transformation is given in a custom high-degree polynomial format.We convert it to a more convenient Euclidean rotation and translation transformation.

Extrinsic calibration between RGB-D cameras is done using color images.Initially,one camera is fixed to the global coordinate system origin.Next,a classical checkerboard-pattern with a known size is used to determine the transformation between initially fixed and other cameras.It is possible that all cameras cannot simultaneously see the checkerboard.In that scenario checkerboard is moved to get a chain of transformations linking all cameras.As the cameras in our experiments are in fixed positions,we can repeat the extrinsic calibration a number of times.With the use of quaternions we can average multiple transformation estimates to achieve more precise results.It also allows measuring standard error of rotation and translation parameters to determine the accuracy of extrinsic calibration.

5 Motion estimation

As detailed in Section 4.2,all image frames received from the cameras are assigned precise timestamps.Due to the consumer-oriented nature of the hardware,we are unable to control shutter trigger time.The result is that the cameras capture fast moving objects at different time.A naive 3D reconstruction of such data would result in one object appearing at slightly different locations simultaneously.

Our solution is to generate new synthetic camera framessuch thatitappearsasifthescene were captured at the same time by all RGB-D devices.Essentially,we interpolate images between consecutive camera frames.Since the interpolation method is continuous,we are free to generate data for any point in time.This also leads to interesting applications such as generating synthetic slow motion videos.

The basic strategy for interpolating depth data from cameras is to estimate scene flow for every camera separately.The depth can then be warped to an interpolated time by applying scaled scene flow vectors to depth points.For an overview of scene flow estimation methods please refer to Yan and Xiang[26].

Unfortunately,the available methods tend to be computationally too expensive to be practical for estimating multiple flow maps in real time.Therefore,we designed our own scene flow estimation method,which trades some estimation quality for speed.In a nutshell,scene flow is estimated by finding correspondences in consecutive depth maps.We generate a mesh of depth points in one frame and warp it iteratively to the closest points on the second depth map frame.Regularization is achieved by imposing some local rigidity constraints on the mesh.

5.1 Scene flow

Scene flow estimation takes as input two consecutive depth maps D and D′from a single RGB-D camera.For the first depth map,D,we generate a dense meshMfrom the depth pixels.Essentially,all neighboring depth points with distance less than a user-set thresholdmtare connected by an edge.Our aim is to warp this mesh so that it matches depth map D′.The warped mesh is denotedM′.The scene flow vectors for depth points then equal the displacements of vertices between meshes M and M′.

To reduce the computational cost of finding correspondences betweenMandD′,we generate multiple mesh and depth scales,{M0,...,Mn}and{,...,},respectively.A mesh scaleMiis found by downscalingMi-1to half size.Downscaling works by removing every second vertex in horizontal and vertical directions.Vertices inMiare joined by edges only if a path of edges exists with length two or less connecting corresponding vertices in mesh Mi-1.The mesh warping strategy begins at the highest scale meshMn,which is iteratively matched to target depth map.The warping parameters are then propagated down to the next mesh scale Mn-1.We store correspondences between vertices at levelsnandn-1 when downsampling.Hence we can simply copy flow data for vertices which exist on both levels.The data for vertices that only exist on leveln-1 can be generated by averaging flow vectors of neighboring edge connected vertices with already copied data.The warp estimation and propagation procedure is repeated at each scale until we reach mesh M0.

The mesh warping procedure works in two steps.First,for all vertices inMiwe find the closest points inusing a grid search and store the new vertex positions in.Since warping is carried out at multiple scales,a fairly small search window of 5×5 suffices for finding good correspondences.Secondly we need to regularize the found correspondences to get more accurate flow vectors.This is done by imposing local rigidity constraints on the meshes.Given corresponding verticesv∈Miandv′∈,we minimize the energy function:

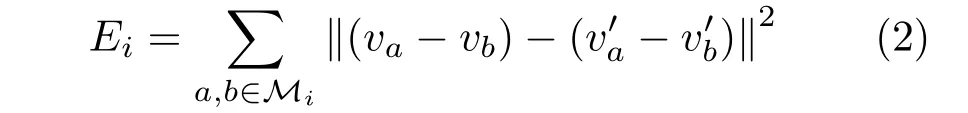
where the sum is over all pairs of vertices connected by edges in the mesh.We carry out energy optimization by gradient descent due to its simplicity.In practice,each gradient descent iteration makes the mesh more rigid.Hence,we can easily tune the mesh rigidity via the number of iterations.

A single warping pass on each mesh level is typically sufficient for slowly moving objects.In the case of rapidly moving objects,the depth has to be warped a long distance from its original location.Since the point correspondence search just selects closest points,many initial matches can be inaccurate.Regularization cannot completely fix bad initial correspondences.Hence it is best to repeat warping a few times,using the last warping result to increase quality.The major steps of flow estimation are shown in Fig.3.

5.2 Depth warping

The final step of motion estimation is to interpolate the depth frames based on the depth map meshes calculated in the previous subsection.

Fig.3 Scene flow estimation using a rapidly moving spherical object.MeshM0is generated from inputDand is transformed through a series of steps,resulting in mesh ,which closely matches the second input depth map D′.

Our system runs at a constant frame rate determined by the user:the reconstruction time is not in fluenced by RGB-D camera frame timestamps.Let the reconstruction time bet. In that case,for each camera separately,we find the consecutive depth framesDandD′from the buffers at timet1andt2,respectively,such thatt1≤t＜t2.The interpolation ratio between those depth frames is then r=(t2-t)/(t2-t1).

Next we generate a new meshM′′by interpolating the vertex positions of meshesM0andM′0.Given the corresponding verticesv ∈ M0andv′∈,the new vertex position for meshM′′is(1-r)v+rv′.The resulting meshM′′can effectively be rendered using standard computer graphics tools to produce a new interpolated depth map.Figure 4 shows an example of interpolation at three different time points using real data.

Fig.4 Depth interpolation.Three interpolated depth maps with interpolation ratios of 0.25,0.50,and 0.75 are generated from input depth maps D and D′.

6 Volumetric reconstruction

3D reconstruction of the collected images requires as input multiple RGB-D camera depth maps,with a common timestamp,taken from different cameras.These images are fused into a triangle mesh model of the scene.Our proposed method is designed to reconstruct the whole scene from scratch on each frame(one frame consists of a set of multiple RGBD images with the same timestamp).That is,no reconstruction data is stored for use in reconstruction of other frames.This approach prevents corruption of the 3D reconstruction by incorrect model tracking.

The reconstruction starts by filtering the depth maps for noisy object edges and estimating the initial surface normals.Next,a block occupancy process if nds regions of space that are likely to contain surfaces,in order to reduce the reconstruction cost.Finally,the surface geometry is estimated and a surface mesh is generated in the main reconstruction process.

6.1 Preprocessing

The input to our reconstruction method consists of depth maps generated from the process presented in Section 5.1.We start with simple filtering of the depth maps and estimation of the initial surface normals.

Depending on the type of RGB-D camera used,the depth maps can contain various types of noise.While our reconstruction method can handle per-pixel measurement noise,completely incorrect surfaces should be avoided.A typical issue with RGB-D cameras is that object edges in depth maps can be noisy or incorrect.Such areas are best avoided,and we alleviate this problem by eroding by one pixel the depth map on object edges.These object edges are found by looking for neighboring depth points separated by a distance greater than a threshold valuemt,also used in Section 5.1. Note that simultaneous use of multiple time-of- flight RGB-D cameras,operating at the same frequency,can cause interference.Most commonly,this interference can make the pixel values periodically vibrate around their true value.In our experiments,the effect was not pronounced,and no specific filter was used to remove such potential artifacts. Details of timeof- flight camera interference are discussed by Li et al.[27],who also proposed a filtering strategy.

The initial surface normals should be estimated at each depth map point location.It is best to calculate the normals for each depth map separately as multiple depth maps may not be perfectly aligned,which may distort the normal estimates.Normal estimation starts by calculating gradients:

and

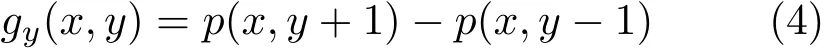
at all depth pixel coordinates. Herep(x,y)is a 3D point corresponding to a depth map pixel at coordinates(x,y).Next,we calculate temporary normals as

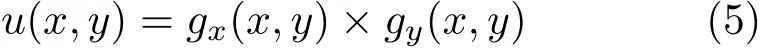
Finally,the initial normals are calculated as a spatially weighted sum over a small window around(x,y)as

wherew(·)represents spatial weighting.We follow Guennebaud and Gross[28]and define the weight function as

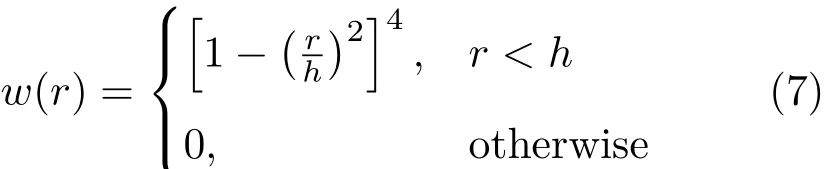
wherehis a constant spatial smoothing factor.The window size for normal calculation can be derived from the spatial smoothing factorhand RGBD camera parameters dynamically for each point.However,in terms of GPU code optimization,we found it best to use a hardcoded 7×7 pixel window for our test scenes.

6.2 Volume hierarchy

Our method is a volumetric reconstruction approach;the reconstructed scene area is defined as the reconstruction volume.This volume can be specified by the user or calculated from the camera positions and their parameters.The smallest volume elements are voxels,arranged in a grid-like fashion.We also define a block as a sub-volume of voxels of fixed size.A block has a uniform number of voxels in all dimensions,for instance,8×8×8.

There are two major reasons for dividing the total volume into blocks.The first reason is that a spatial hierarchy allows us to determine the occupied volume regions,which need to be reconstructed.In other words,we eliminate the need for expensive voxel calculations in areas where there are no depth map points and hence no surfaces.This method is simpler than using octrees ork-d trees and can be computed quickly.The second reason concerns storing voxel values.We prefer not to store voxel data in the GPU main memory as it is expensive and we have no use for this data when reconstructing the next frame.Our method is more light-weight than other proposed volume memory reduction schemes[29,30].However,it is important to note that we do need voxel values to generate the mesh.The size of a block of voxels is low enough to permit its temporary storage.Furthermore,we can utilize modern GPU features in this scenario to speed up the processing.

Modern GPUs have multiple types of memory with different characteristics.Global memory is plentiful and is persistent from allocation to deallocation but has slow access time.Shared memory,on the other hand,has limited availability of just tens of kilobytes,and the data is not persistent during program execution,but it has much faster access time.According to GPU manufacturer documentation,recent GPUs such as those in the Nvidia GeForce range have roughly 100 times lower shared memory latency than for uncached global memory.We leverage this to greatly accelerate 3D reconstruction.Typical volumetric reconstruction methods store per-voxel data in GPU global memory.This data needs to be read and written when estimating surfaces.Furthermore,mesh generation also requires multiple lookups of the voxel values.In contrast,our method is designed to use only shared memory to store voxel data.

Using the shared memory comes with certain restrictions.Most importantly,the data is stored only for the duration of GPU thread group execution.This means that after any voxel value calculation,we must immediately run mesh generation on the same voxels.As the amount of shared memory is very limited,this limits maximum block size.

Our mesh generation method,which uses the marching cubes algorithm,can only generate triangles between neighboring voxels. Essentially,every possible 2×2×2 voxel sub-volume is processed to yield zero or more triangles.We can run marching cubes inside a block of voxels but not at block edges.However,using the shared memory for block voxel storage means that we cannot look up the voxel values of neighboring blocks.We solve the problem similarly to Ref.[30]and make all blocks overlap each other by one voxel in each direction.As an example,if a block consists of 8×8×8 voxels,then all blocks are laid out with spacing of seven voxels on all axes.

Because the voxel blocks overlap,some voxels are processed several times as parts of different blocks.We can calculate the theoretical worst-case overhead ass3/(s-1)3,wheresis the size of the block in voxels.In the case of an 8×8×8 voxel block,we get 49%processing overhead.While the extra processing might seem considerable,the savings from not having to store and load voxels in global memory is greater.However,the block sizesshould be chosen with the balance of shared memory usage and processing overhead in mind.

6.3 Block occupancy

To determine which blocks of voxels are likely to contain surfaces,we count the number of points found in each block.A three-dimensional array of integers is allocated with one entry per block in the reconstruction volume.Assuming we are using a GPU that supports atomic operations,we project all depth map points to the reconstruction volume.Atomic addition,ATOMICADD(m,n),which adds the valuento some array locationm,is used to sum the number of points in each block in parallel.Note that because the blocks overlap by one voxel on each side,we must detect when points are on edges and add them to other block counts as well.The procedure is summarized in Algorithm 1.An example of finding the number of points inside the blocks is depicted in Fig.5.

?

Next we need to find a list of non-empty blocks so that they can be reconstructed.We iterate over all blocks to determine whether the point count exceeds a constant thresholdbt.This threshold acts as a coarse point cloud filter.In practice,however,blocks tend to have relevant surfaces even at quite low point counts and hence settingbt=1 is recommended.Again we utilize the atomic add operation to create a list of occupied block coordinates.Details are given in Algorithm 2.

Fig.5 Visualization of blocks to be reconstructed.Left side shows the input point cloud and the right side shows the corresponding non-empty blocks.

?

6.4 Reconstruction

The main part of scene reconstruction consists of estimating the surface geometry and generating the respective triangle meshes.The surfaces are defined implicitly using a signed distance function(SDF).The meshing algorithm can then find a zero-level set of SDF and output triangles.

We estimate SDF for each voxel by sampling nearby points from all RGB-D cameras.State-of-the-art dynamic scene reconstructions using signed distance functions(e.g.,Refs.[6,7])typically use only one depth map point per camera to update single voxel values.This method works well only if the SDF is updated over multiple frames.Because our volume is not stored between reconstructions,this approach does not suit our needs.We choose to estimate the local surfaces using MLS,which samples many points in the neighborhood of the voxel.

To estimate the local surface,we first need to retrieve depth pointspiand the corresponding initial surface normalsnifrom the neighborhood of a given voxel positionp.Following Kuster et al.[23],we projectpto each RGB-D depth map and retrieve a u×usquare block of depth pointspiand normals niaround the projected point.

For the actual surface estimation,we follow the moving least squares formulation put forward in Ref.[31].Given a voxel positionp,some corresponding pointspi,and some normalsni,we can calculate a new weighted position:

and weighted normal:

?

wherew(r)is the spatial weighting function previously defined in Eq.(7)for use in normal estimation.

We also define a voxel confidence value simply as

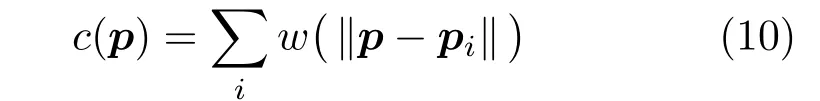
Finally,the implicit surface distance function is given as

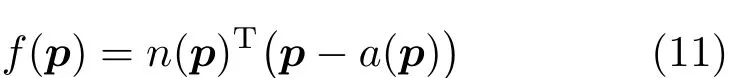
In cases where the confidence valuec(p)is below a constant user-specified thresholdct,we markf(p)as invalid.This effectively removes surfaces that do not have enough points for an accurate estimation.We store the SDF valuef(p),the normaln(p),and the confidence valuec(p)for each voxel.The normal is stored so that there is no need to estimate the surface normal again during meshing.Also the confidence value can be used to generate smooth object edges during rendering.

To generate the mesh,we use marching cubes triangulation[32].Every possible 2×2×2 voxel sub-volume of the block is passed to triangulation.The marching cubes method decides which triangles to create between each voxel based on SDF values.If any valuesf(p)are found marked as invalid,then no triangles are output.All valid triangles are written to a global buffer and include a point locationp,a normaln(p),and a confidencec(p)attribute for each vertex.

Both surface estimation and mesh generation are summarized in Algorithm 3.The major steps of reconstruction are also visualized in Fig.6.

Fig.6 Reconstruction of an 8×8×8 voxel block using real-world data.(a)Input point cloud data;colors mark different RGB-D cameras;(b)MLS voxel values(only negative voxel values are visualized);(c)meshing result after marching cubes triangulation.Note that the outlier points on the left side of the block are successfully excluded from the final result.

6.5 Rendering

The reconstructed scene is rendered solely using triangles generated by the process described in the previous subsection.The included normals can be used to shade the 3D model under lighting.

The 3D mesh can contain discontinuities at edges of thin objects or due to limited depth map coverage of the scene.A naive rendering of such areas will result in jagged edges.This is because marching cubes has no native way of handling discontinuities.However,we can use the confidence valuec(p)of the vertices to smoothly cut offtriangles at a user-defined thresholdcr.Optionally,the edges can be smoothly made transparent using alpha blending together with an order-independent transparency technique such as depth peeling[33].Different ways of handling edge rendering are visualized in Fig.7.

Fig.7 Edge rendering methods.(a)The mesh is rendered;(b)mesh triangles are cut offat a user-defined confidence value;and(c)mesh triangles smoothly transition from opaque to transparent based on confidence value.

7 Results

All of our experiments were conducted on a server with an Intel i7-5930K CPU,32 GB of RAM,and an Nvidia GeForce GTX 1080 Ti graphics card.The client computers were Intel NUC7i3 machines with an Intel i3-7100U CPU and 16 GB of RAM.For RGBD cameras,we exclusively used Microsoft Kinect 2 devices.

The system performance characteristics for a typical scene recorded with four RGB-D cameras can be seen in Table 1.Because our pipeline is completely executed on the GPU,precise statistics for each process step can be obtained by OpenGL timer queries.We used the system parameters given in Table 2,which were tuned to obtain maximum reconstruction quality while retaining a real-time frame rate.

An important aspect of our reconstruction system is the ability to handle scenes with significant dynamic content.This includes fast-moving objects as well as changing scene topology.Figure 8 showsthe effectiveness of the approach.A selection of challenging situations is shown in Fig.9 and in the Electronic Supplementary Material(ESM).Rapid movements of objects are correctly reconstructed thanks to our depth frame interpolation method.

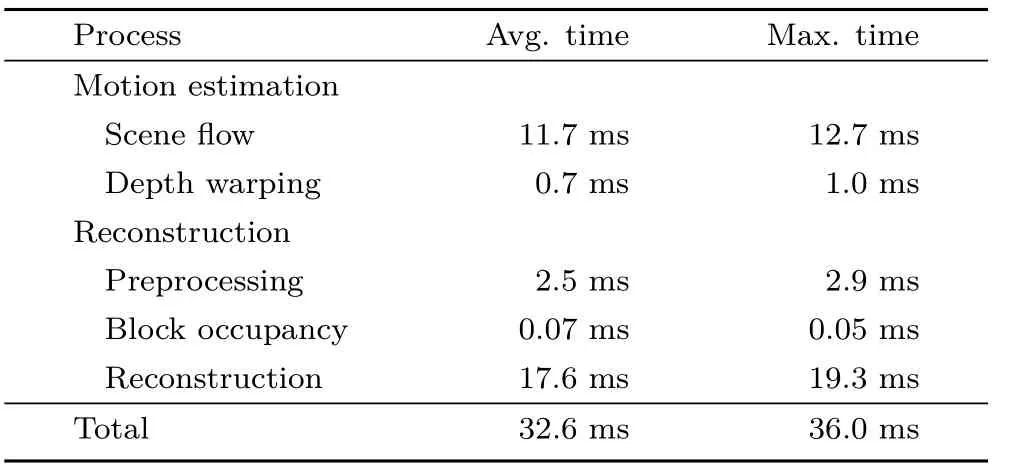
Table 1 Performance

Table 2 Recommended parameters

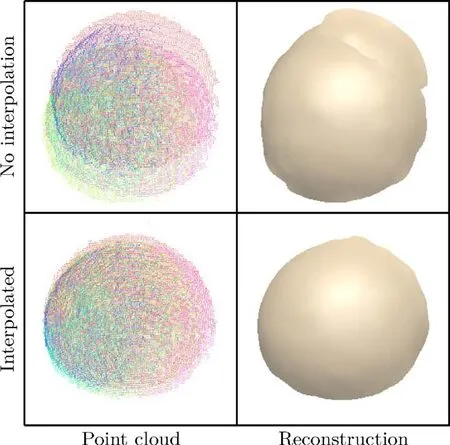
Fig.8 Frame interpolation using a fast-moving spherical object.Without interpolation(above),the point clouds from the different cameras are not aligned.Using interpolation(below),the point clouds are aligned and the object is correctly reconstructed.

Human actor reconstruction can be seen in Fig.10 and in the accompanying video in the ESM.Source data was taken from a publicly available dataset,courtesy of Alexiadis et al.[21].The resulting model has good quality where visibility from cameras is good.However,as our method is designed to be very general,we do not use human templates to fill missing surface areas.

Large scenes can also be reconstructed with our method in real time.Figure 11 shows a room of size 10 m×3 m×3 m.Movements can more clearly be seen in the supplementary video in the ESM.The scene can be reconstructed in real time mostly because of the block occupancy test,which avoids the need to reconstruct empty spaces.Moreover,because we do not store the reconstruction volume,the memory cost is low.For a volume with 2×107voxels,we only need to store block occupancy,taking 153KB,and block index data,taking up to 457KBof memory.The rest of the memory usage is related to input depth maps and normals,and the output triangle mesh.

The number of systems to which we can compare our method is limited. Recent dynamic scene reconstruction methods,especially ones that utilize truncated signed distance volumes,require fusing depth data over multiple frames and are not designed to handle cameras with unsynchronized shutters.In addition,we are restricted in choosing comparative methods as our scenes contain backgrounds and highly non-rigid objects,such as cloth,for which template generation is very difficult.

We compared our 3D reconstruction method with another MLS method that uses mesh zippering[24]and with Poisson surface reconstruction[19].Some results for highly dynamic and large scenes are shown in Fig.11 and Fig.12,respectively.These methods were chosen for their ability to reconstruct entire scenes from only one depth frame per RGB-D camera.In terms of quality,mesh zippering tends to have rough edges at surface discontinuities.Additionally,joining meshes can fail in some areas with complex geometry,resulting in small holes in the meshes or incorrectly generated triangles protruding from surfaces.The Poisson method works off-line,taking between 2 and 4 s to reconstruct the scenes in Fig.11 and Fig.12 when the reconstruction depth parameter is set to 8.This method has the ability to complete a surface even when point cloud data is missing from some scene areas.While this feature can be beneficial in repairing some areas of the generated mesh,it also has drawbacks.Firstly,real-world scenes tend to be topologically open and have many boundaries.These areas are incorrectly reconstructed by the Poisson method.Secondly,repairing surfaces is an underdetermined problem and holes in geometry can be filled in various ways.This results in temporally inconsistent surfaces.

Fig.9 Reconstructing highly dynamic scenes:(a)a ball is thrown at a cloth curtain;(b)a cloth is shaken;(c)a ball bounces offthe ground;and(d)a large piece of paper is torn apart.

Fig.10 Reconstruction of human actors in various poses.Capture data is courtesy of Alexiadis et al.[21].Above:part of“Alexandros” scene.Below:part of“Apostolakis1” scene.In general,the models are correctly reconstructed.However,some smaller details are missing due to lack of visibility from cameras.

Fig.11 Reconstructing a fast ball throw in a large scene with five RGB-D cameras:(a)shows our method together with camera positions,(b)uses MLS-based mesh zippering[24],and(c)shows Poisson reconstruction method[19].

Fig.12 Comparison of 3D reconstruction methods:(a)shows our method,(b)uses MLS-based mesh zippering[24],and(c)shows the Poisson reconstruction method[19].Zippering shows bad edge quality and occasionally has incorrect triangles protruding from surfaces.The Poisson method tends to over-smooth areas and incorrectly handles open scenes.

8 Conclusions

In thispaperwedemonstrated anovel3D reconstruction system that can reconstruct highly dynamic,large scenes in real time.We solve the problem of combining data from multiple consumer RGB-D cameras lacking synchronized shutters.Our reconstruction method is designed to be memory efficient and provides real-time performance.

Theproposed method may haveusesin teleconferencing,virtual reality,or free-viewpoint television applications.It allows the use of consumer RGB-D devices for scene capture rather than requiring custom-made camera rigs.Finally,the synthetic slow-motion playback could be useful in performance-capture applications.

Electronic Supplementary MaterialSupplementary material demonstrating our method in both highly dynamic and large scenes is available in the online version of this article at https://doi.org/10.1007/s41095-018-0121-0.