含新能源接入的配电网中储能系统协调控制策略

孙 舟，田贺平，王伟贤，潘鸣宇，张 禄

(国网北京电力科学研究院，北京 100075)

0 引 言

随着化石能源的日益枯竭，光能、风能等可再生能源发展迅速，其发电比例正逐渐增加。储能技术被认为是解决目前和将来电网中新能源穿透率持续增加等问题的可行方案[1]，电池储能因其独特的性能已成为优先发展方向之一[2]。

配电网中的电池储能系统(battery energy storage system，BESS)可以减小由于新能源接入带来的波动性，平滑负荷，并且可以通过在电价高峰期放电，在电价低谷期充电来获得一定收益。对于配电网中的电池储能系统，研究多集中于容量配置上。文献[3]考虑了超级电容和蓄电池的混合储能系统在配电网中的容量配置问题。文献[4]综合考虑储能与光伏出力、负荷间时序的配合，进行储能系统的选址和定容。文献[5]使用改进多目标粒子群算法求解储能系统在配电网中选址定容的多目标优化问题，但是文章对储能系统具体的运行控制策略并未有太多说明。文献[6]研究了主动配电网背景下储能系统的优化配置方法，分别以削峰填谷、改善电压质量为目标，建立了相应的数学模型，用改进的粒子群算法进行求解，但是并未考虑储能系统的运行和投资成本。关于配电网中储能系统的优化控制策略，相关研究不多，主要集中在单目标优化问题上，文献[7]考虑了配电网中储能系统实现降低网损的功能，提出了一种基于锥优化理论的求解方法，求解出储能系统最优出力。文献[8]考虑了储能电站接入配电网对网损和负荷曲线的影响，建立了电池储能站优化模型，利用遗传算法求解储能电站的最优出力。关于多目标优化问题，常用的方法有多目标进化算法、多目标粒子群算法、多目标遗传算法等[9-11]，关于配电网中储能系统的多目标优化问题，相关研究较少，文献[12]考虑了电池储能系统对配电网负荷曲线和网损变化的影响，以网损最小和削峰填谷效果最好为目标构建储能电池双目标优化运行模型，但是仅考虑了储能系统对负荷削峰填谷，并未考虑新能源的接入。

本文对含新能源的配电网电池储能系统的协调控制策略进行研究，针对配电网有功功率波动、新能源接入点电压波动建立了多目标优化模型，将储能系统的出力作为控制变量，使用NSGA-II算法求解其Pareto非支配解集，实现多个储能系统的协调控制。最后，通过IEEE14节点的算例分析，表明本文策略的有效性。

1 配电网运行多目标优化模型

随着新能源发电比例的逐渐增加，风电、光伏等具有间歇性和波动性的电源接入会对配电网的稳定运行带来不利影响。在新能源渗透率较高时，配电网入口处有功功率会出现大幅波动，对区域电网的电压和频率稳定带来冲击；另外，在配电网中，新能源接入节点的电压会因为其波动性和间歇性受到影响，影响该节点所供负荷的电能质量，因此可以选择配电网有功功率波动和新能源接入点电压波动作为优化目标。储能是提高电网对新能源接纳能力的有效手段，通过对储能系统的合理控制，可以减小新能源间歇性和波动性给电网带来的不利影响。一般情况下，储能系统都是和风电场或光伏电站配合，实现平抑波动，跟踪调度等功能，但是不同储能电站之间是孤立的，仅仅根据自己所配合的风/光电源进行控制，随着智能电网的发展，不同风电场或光伏电站的电池储能系统的相互配合及协调控制成为可能，因此选择储能电站的出力作为控制变量。

1.1 目标函数

1.1.1 配电网有功功率波动优化

研究配电网功率波动时，认为大电网是稳定的，只考虑功率变化对配电网内部节点的影响，将配电网入口母线作为平衡节点进行潮流计算，则配电网整体功率即为平衡节点输出功率。由于新能源出力具有不确定性且无法准确预测，所以直接考虑一个调度周期内功率的波动是不易的，故可以用滤波算法设定参考值，用实际值和参考值的差值实时表征功率波动情况，如下所示：

(1)

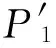
(2)

minF(t)=|P1(t)-P1，ref(t)|

(3)

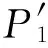
1.1.2 新能源接入节点电压波动优化

新能源接入节点受其输出功率波动的影响最为直接，这些节点的电压波动程度可以用下式综合表示：

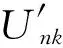
(4)

(5)

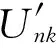
1.2 约束条件

1.2.1 有功功率平衡约束

配电网的运行满足有功功率平衡的约束，即

P1+∑Pnew+∑PBESS=∑Pload+∑Ploss

(6)

式中:Pnew表示配电网中新能源出力；PBESS表示配电网中储能系统的出力，其值大于0表示放电，小于0表示充电；Pload表示负荷消耗的有功功率；Ploss表示线路上损失的有功功率。

1.2.2 储能系统功率上下限约束

储能系统充放电功率是有限制的，要满足上下限约束，即

-PBlim≤PBESS≤PBlim

(7)

式中:PBlim表示储能系统允许的充放电最大功率，一般为额定功率，单位为MW。

1.2.3 储能系统荷电状态约束

对于储能系统来说，荷电状态(state of charge，SOC)表示剩余电量百分比，过度充电和过度放电会严重影响电池循环寿命，所以需要对储能电池的SOC进行限制，其计算方式和约束条件如下：

(8)

SOCmin≤SOC(t)≤SOCmax

(9)

式中:E表示储能系统的容量，单位为MWh；SOCmin和SOCmax分别表示储能荷电状态合理区间的上限和下限，一般可取SOCmin为10%，SOCmax为90%。

1.3 储能系统的SOC反馈控制

由于新能源出力的不确定性，在一个完整调度周期内考虑储能系统的出力计划是不易的，故需要对储能系统的出力附加SOC反馈，在SOC较低的时候减少放电，在SOC较高的时候减少充电，使得储能电池的荷电状态维持在合理的区间内，以完成整个调度周期内的工作。具体控制策略如下所示：

(10)

式中:PSOC,BESS为经过附加SOC反馈后储能系统的出力值；λ和η为控制系数，取值和SOC有关，如图1所示。

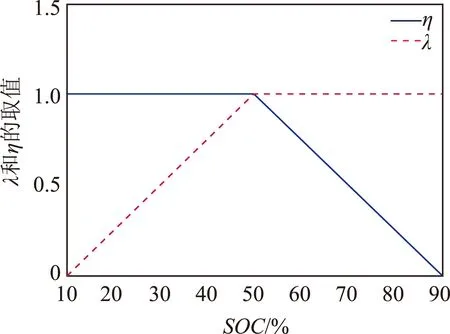
图1 λ和η的取值

图1表示，在SOC值超过50%时，储能系统的充电功率随着SOC值的增大在原给定出力的基础上缩减，放电功率则和给定功率一致；在SOC值低于50%时，储能系统的放电功率随着SOC值的减少而上缩减，充电功率则和给定功率一致，这样使得储能电池的SOC值可以一直维持在合理的区间内。

2 多目标优化问题求解

2.1 Pareto最优

Pareto最优指的是资源分配的一种理想状态，一般情况下，多目标优化模型的各目标函数之间在最优化方向上存在冲突，难以得到绝对最优解，但通常存在一个 Pareto 最优解集[13]。如果对于某组解，在试图改进任何目标函数的同时必然会削弱其他目标函数，则该组解就被称为Pareto非支配解，反之，则称为支配解，而Pareto最优解集就是Pareto非支配解的集合，又称Pareto前沿。一个两目标优化的Pareto前沿如图2所示。

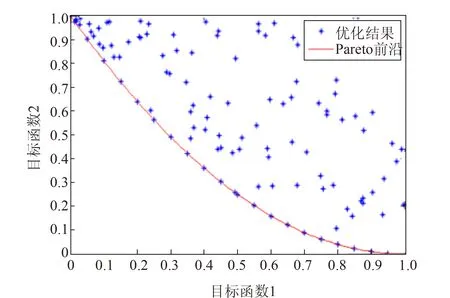
图2 两目标优化的Pareto前沿

在图2中，Pareto前沿上的解无法使目标函数1和2同时减小，若使某个目标函数减小，必然伴随着另一个目标函数的增大，属于非支配解。而在Pareto前沿上方区域的解，是支配解，可以在某个目标函数不增大的情况下，使另一个目标函数继续减小。

2.2 NSGA-II算法

非支配排序遗传算法(non-dominated sorting genetic algorithm，NSGA)是一种基于 Pareto最优概念的遗传算法，NSGA 与基本遗传算法的最大区别在于，NSGA 算法在进行选择、交叉、变异等操作之前，对种群中个体之的支配关系进行了分层，通过这种方法，能够选择较优的个体[14]。NSGA-II算法NSGA的改进，通过增加精英保留策略、计算拥挤距离值作为密度估计策略和快速非支配排序策略，解决了NSGA算法参数选取难和运行效率低等缺点[15]，是多目标进化算法中应用最为广泛的算法。

2.3 求解流程

针对配电网有功功率波动、新能源接入点电压波动两目标优化问题，使用NSGA-II算法优化储能系统出力的流程图如图3所示。

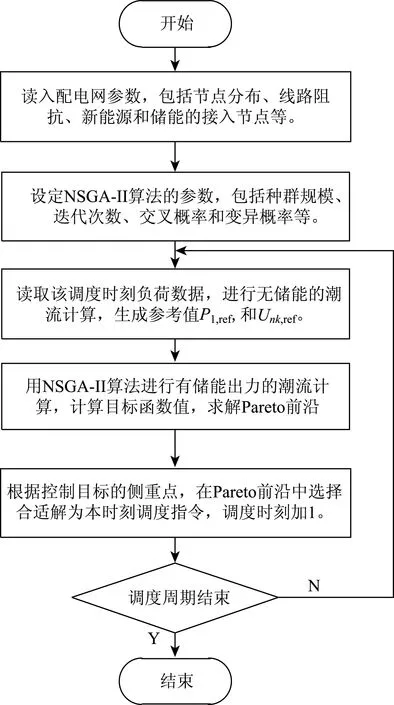
图3 求解储能系统出力流程图

如上图所示，首先设定初始数据，即配电网和NSGA-II算法的各种参数；之后读取该时刻负荷数据，在假定无储能出力的情形下，计算配网的潮流，以获得配电网有功功率波动、新能源接入点电压波动两个控制目标的参考值；接着用NSGA-II算法求解不同储能出力时的潮流，计算目标函数值，获得Pareto前沿；最后根据控制目标的侧重点，在Pareto前沿中选择合适的解作为该时刻储能的出力，完成本时刻储能系统的调度。

3 算例分析

本文选取IEEE14节点配电网进行分析，结构如图4所示。该配电网电压等级为23kV，1为平衡节点，其电压标幺值为1.05∠0°，总负荷为28.7+j7.75MVA，归算到以100MVA为基底的线路参数和额定负荷数据如表1和表2所示。在节点2和节点8接入新能源，其中节点2接入光伏和储能，光伏功率为6MWp，BESS1的额定功率为2MW，容量为6MWh；节点8接入风电和储能，风电功率为10MW，BESS2的额定功率为3MW，容量为9MWh。一个完整调度周期为一天，调度时间间隔为15min，共分为96个调度时刻，储能系统SOC初始状态为50%，主要负责削峰填谷，当新能源发电超过本节点负荷的时候充电，反之则放电。

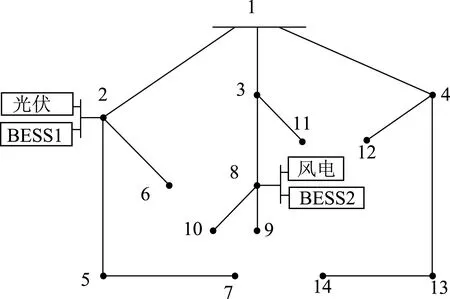
图4 IEEE14节点配网图

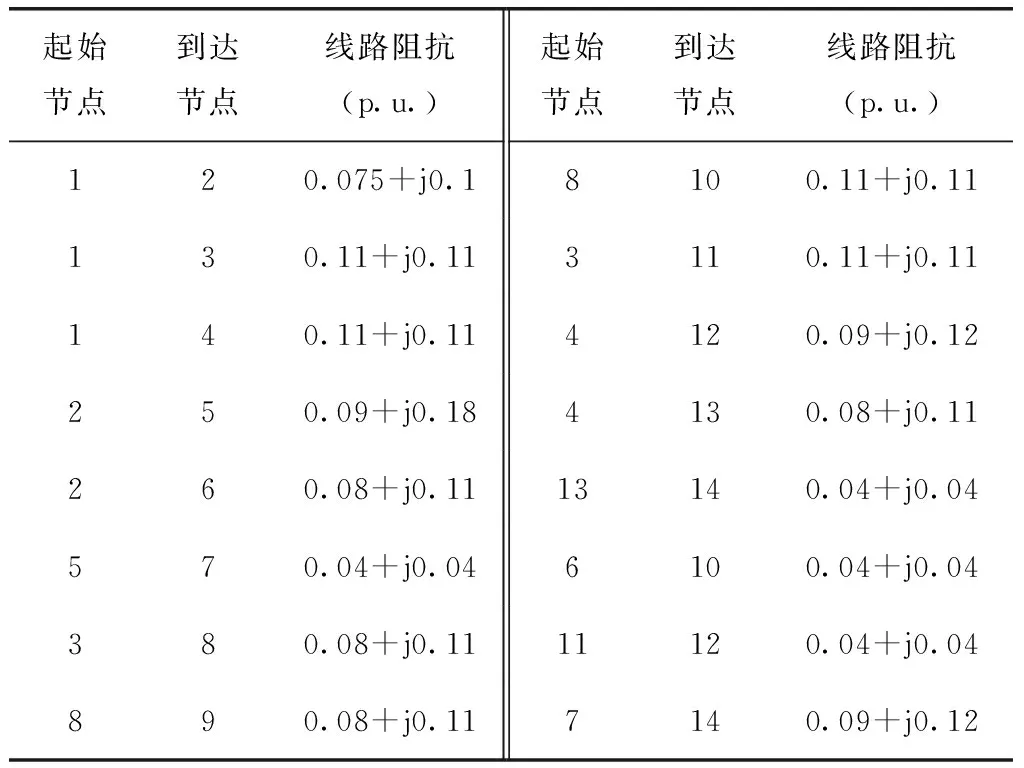
起始节点到达节点线路阻抗(p.u.)起始节点到达节点线路阻抗(p.u.)120.075+j0.18100.11+j0.11130.11+j0.113110.11+j0.11140.11+j0.114120.09+j0.12250.09+j0.184130.08+j0.11260.08+j0.1113140.04+j0.04570.04+j0.046100.04+j0.04380.08+j0.1111120.04+j0.04890.08+j0.117140.09+j0.12

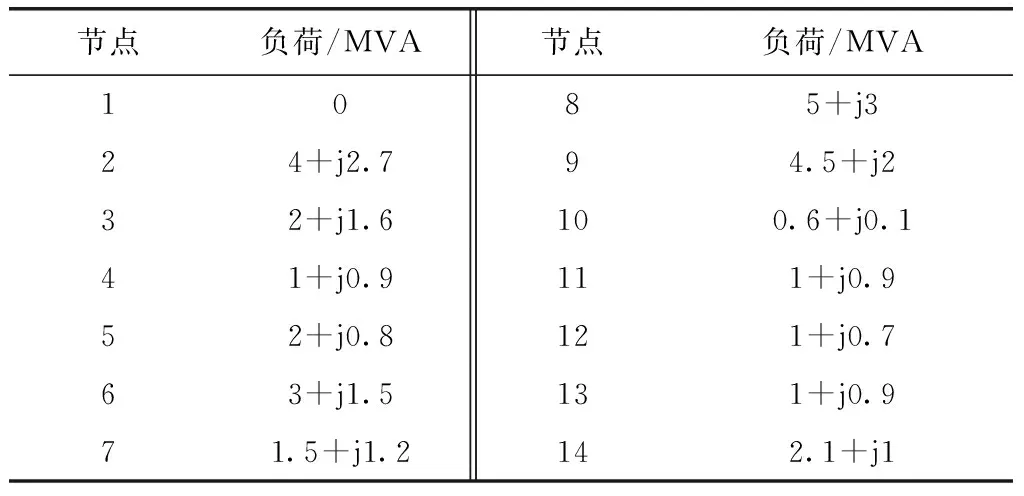
表2 负荷数据

配电网典型负荷曲线如图5所示，光伏出力曲线和风电出力曲线分别如图6和图7所示。

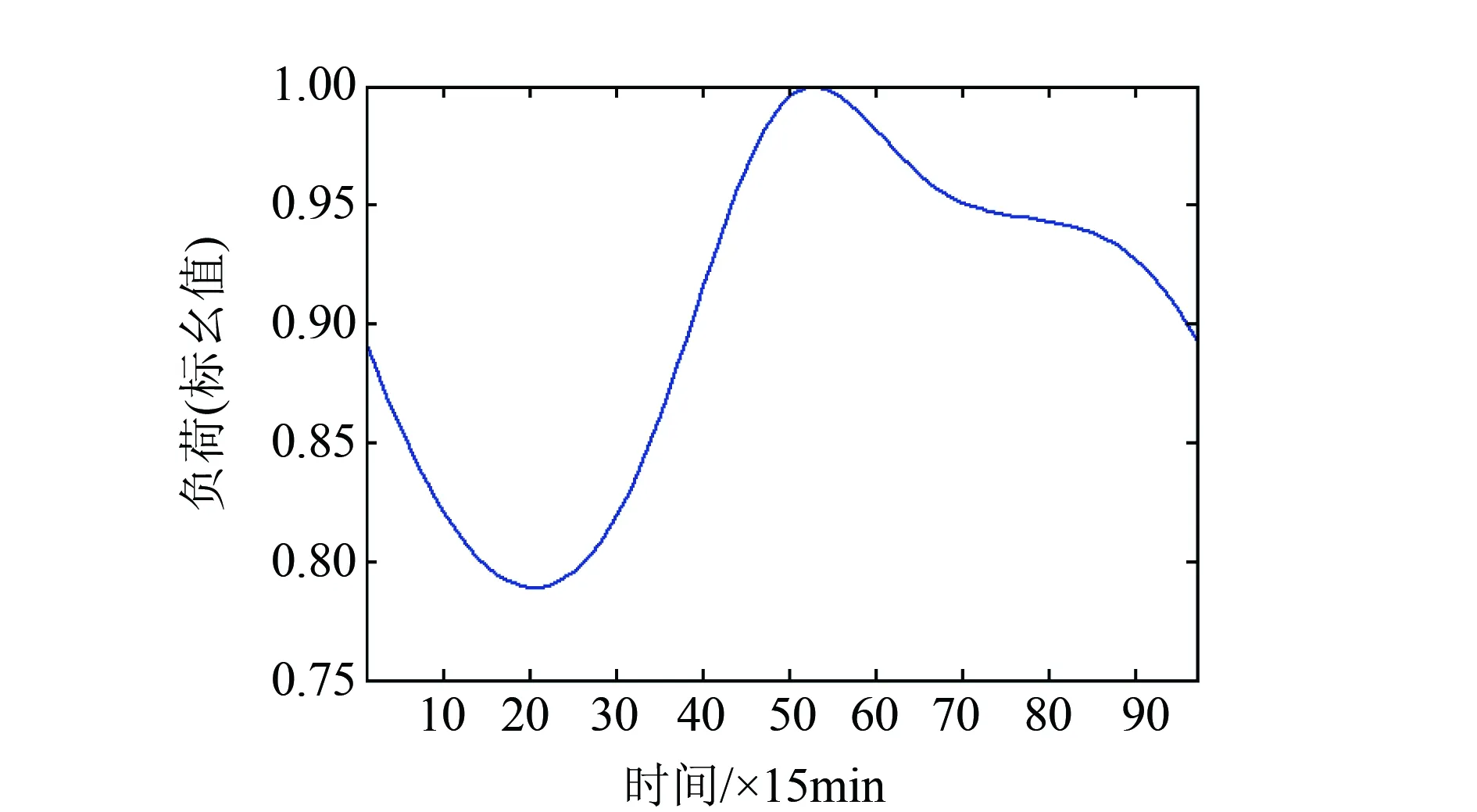
图5 配电网典型负荷曲线

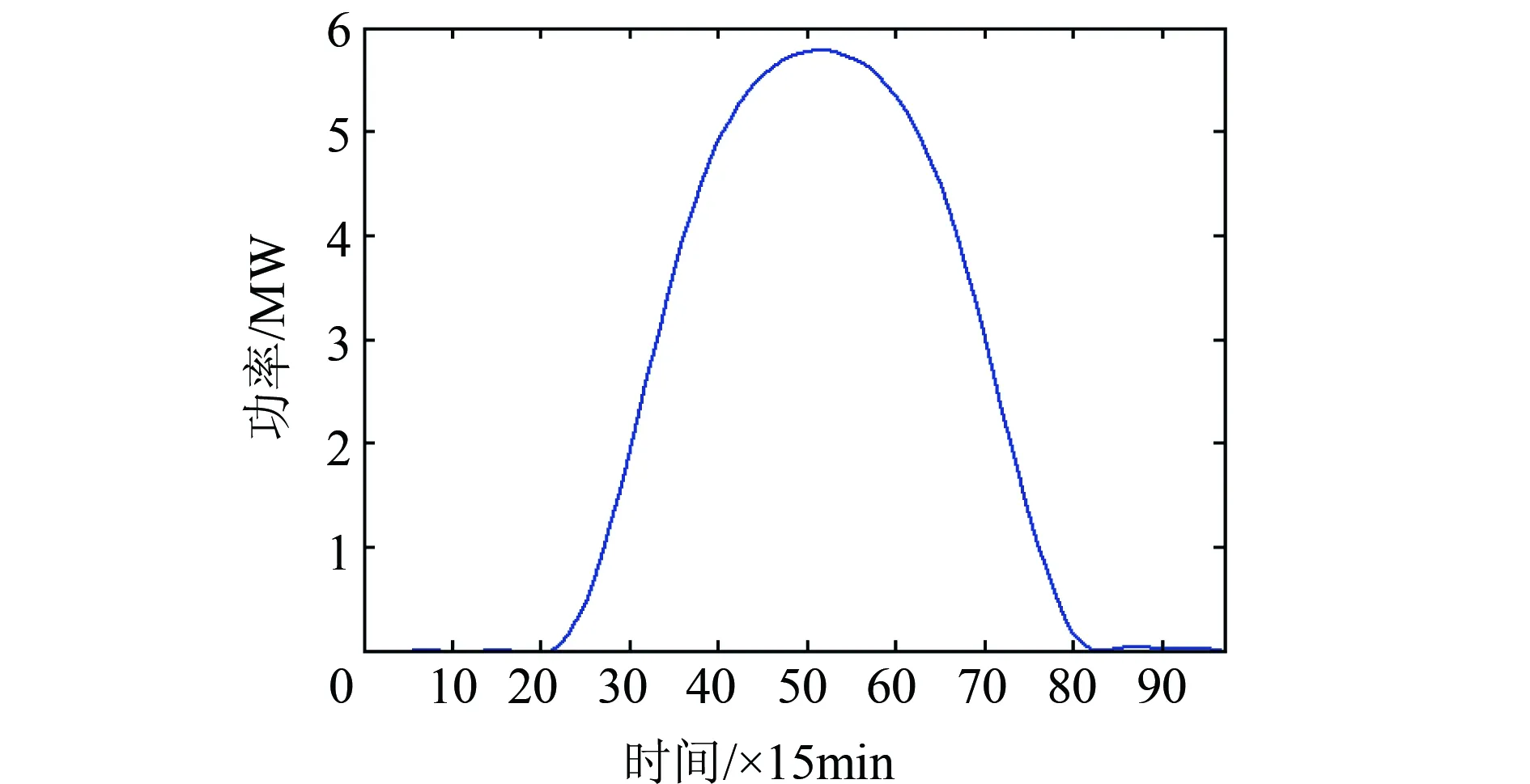
图6 光伏出力曲线

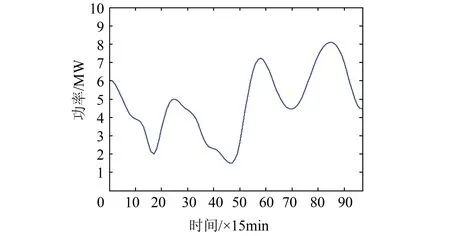
图7 风电出力曲线

3.1 储能系统不出力

先分析该算例储能系统不出力时的情况，进行潮流计算，一个完整调度周期内配电网有功功率波动和新能源接入节点电压波动结果如图8和图9所示。

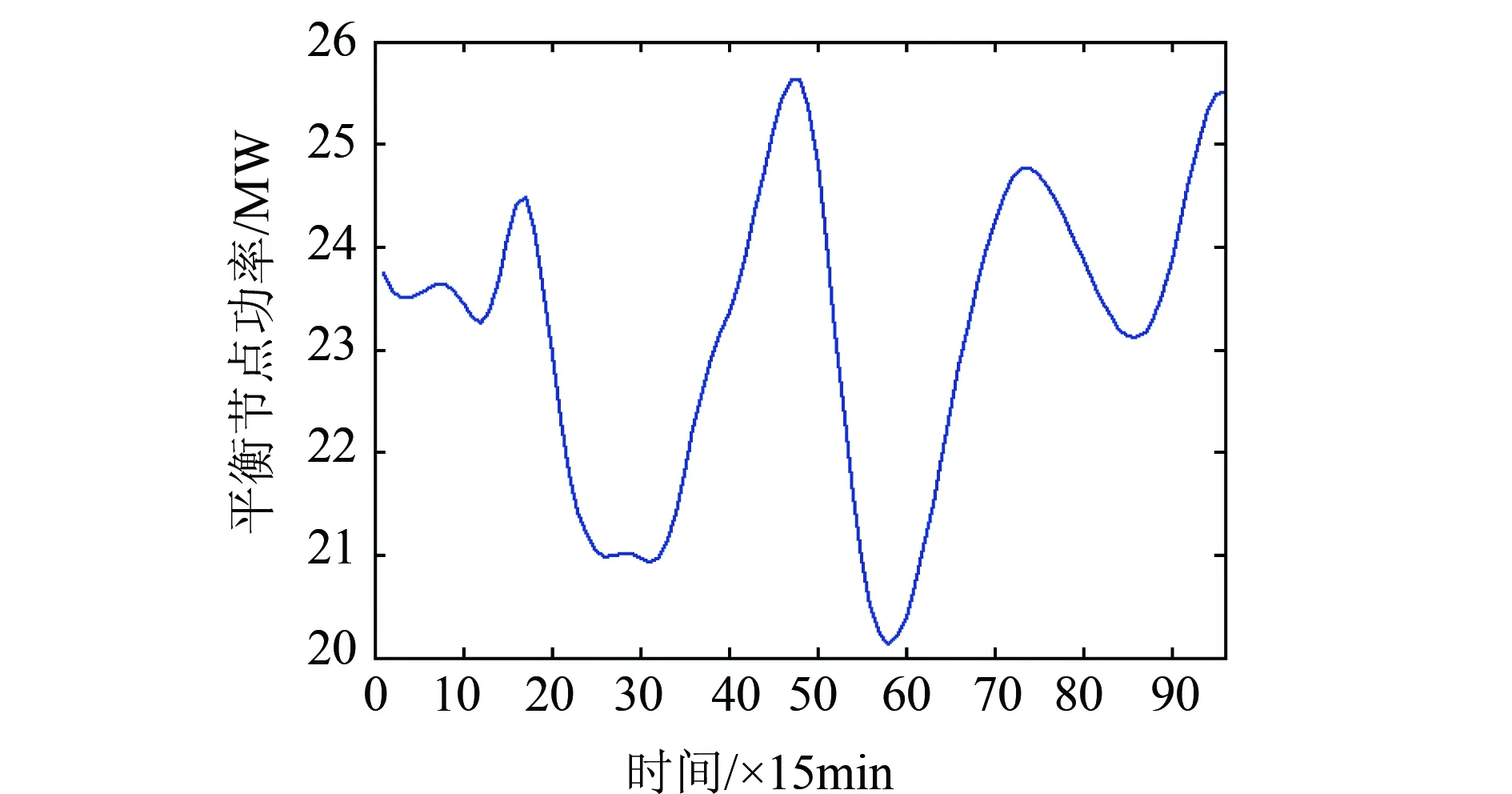
图8 无储能时配电网有功功率

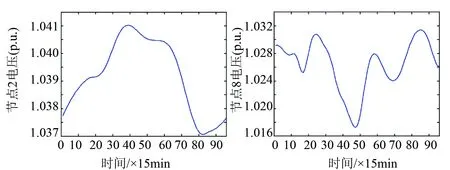
图9 无储能时新能源接入节点电压

由图8可以看出，受新能源接入的影响，配电网有功功率波动幅度较大，如果电网中新能源渗透率较高，含新能源的配电网均存在功率大幅波动的情况，会对电网的稳定性造成冲击。由图9可以看出，因为光伏和风电发出的功率仅为有功功率，功率因数为1，在本算例中，新能源接入节点的电压波动幅度不大，节点2和节点8电压的极差均未超过额定电压的2%。

3.2 储能系统孤立控制

当BESS1和BESS2只负责各自节点削峰填谷的时候，配电网有功功率波动和新能源接入节点电压波动分别如图10和图11所示，BESS1和BESS2的SOC变化情况如图12所示。

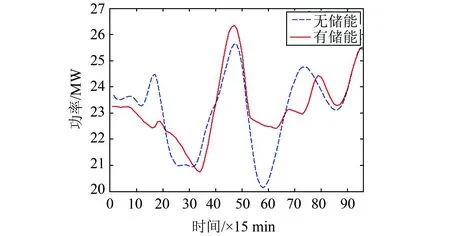
图10 孤立控制时配电网有功功率

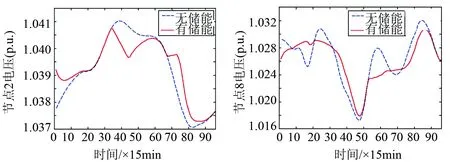
图11 孤立控制时新能源接入节点电压

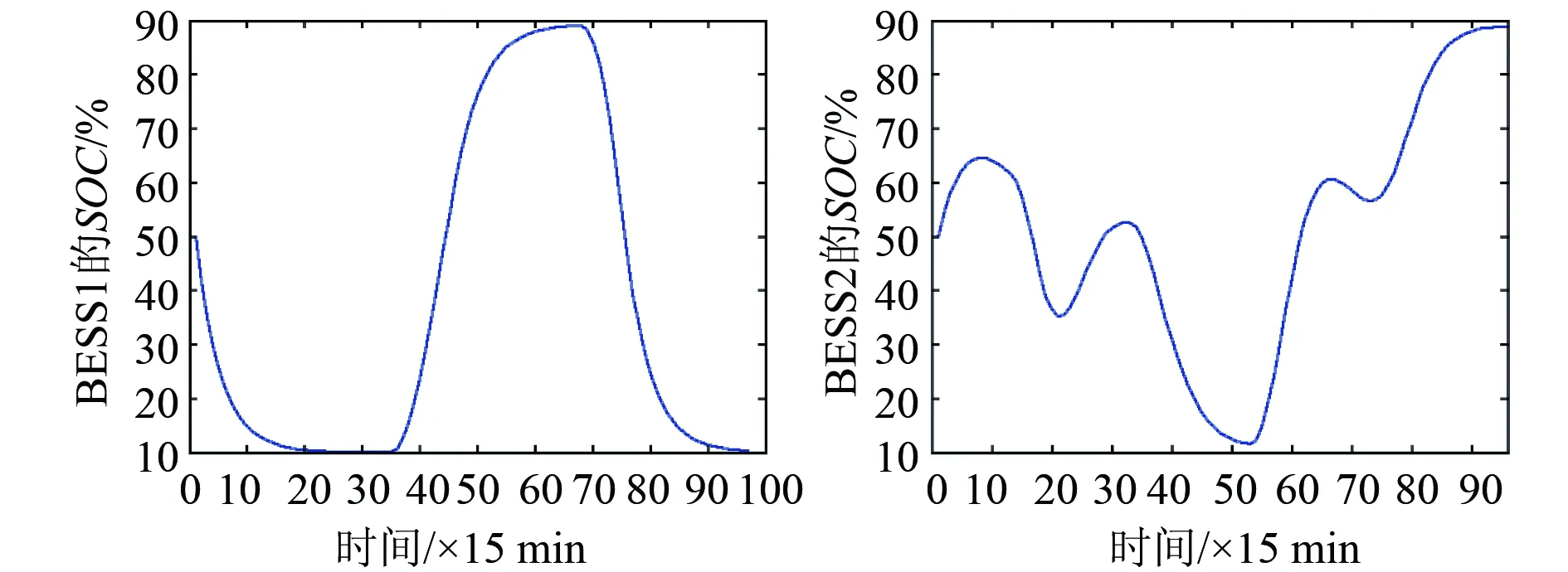
图12 孤立控制时储能系统SOC变化情况

可以看出，孤立控制的储能系统在一定程度上可以减小功率波动和电压波动，但是效果并不明显，甚至有时会放大波动程度。

3.3 储能系统协调控制

设定NSGA-II算法的种群规模为30，迭代次数为50，交叉概率为0.8，变异概率为0.3，取滤波系数α和β均为0.05，对于某一调度时刻，可以求出其Pareto前沿，例如调度时刻为96时求解的Pareto前沿如图13所示。求解出Pareto前沿后，可以根据不同的侧重点，选取储能的协调控制方案。

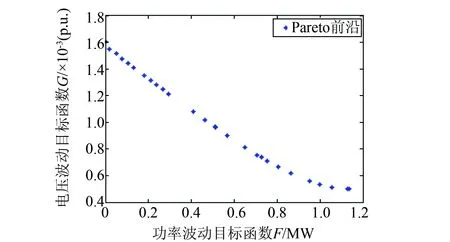
图13 调度时刻为96时所求Pareto前沿

由3.1节可知，对于本算例而言，配电网有功功率波动较大，而新能源接入节点的电压波动幅度较小，因此选择优化配电网有功功率波动作为首要控制目标，在Pareto前沿中选择使配电网功率波动目标函数最小的储能出力，配电网有功功率波动和新能源接入节点电压波动分别如图14和图15所示，SOC变化情况如图16所示。

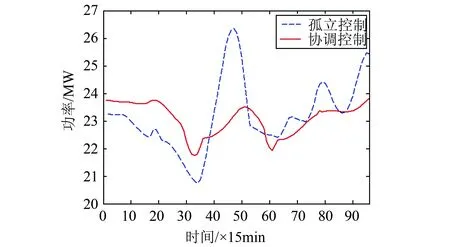
图14 协调控制时配电网有功功率

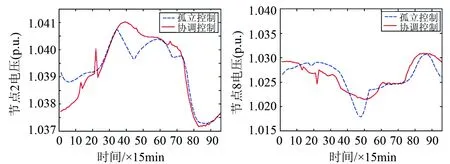
图15 协调控制时新能源接入节点电压

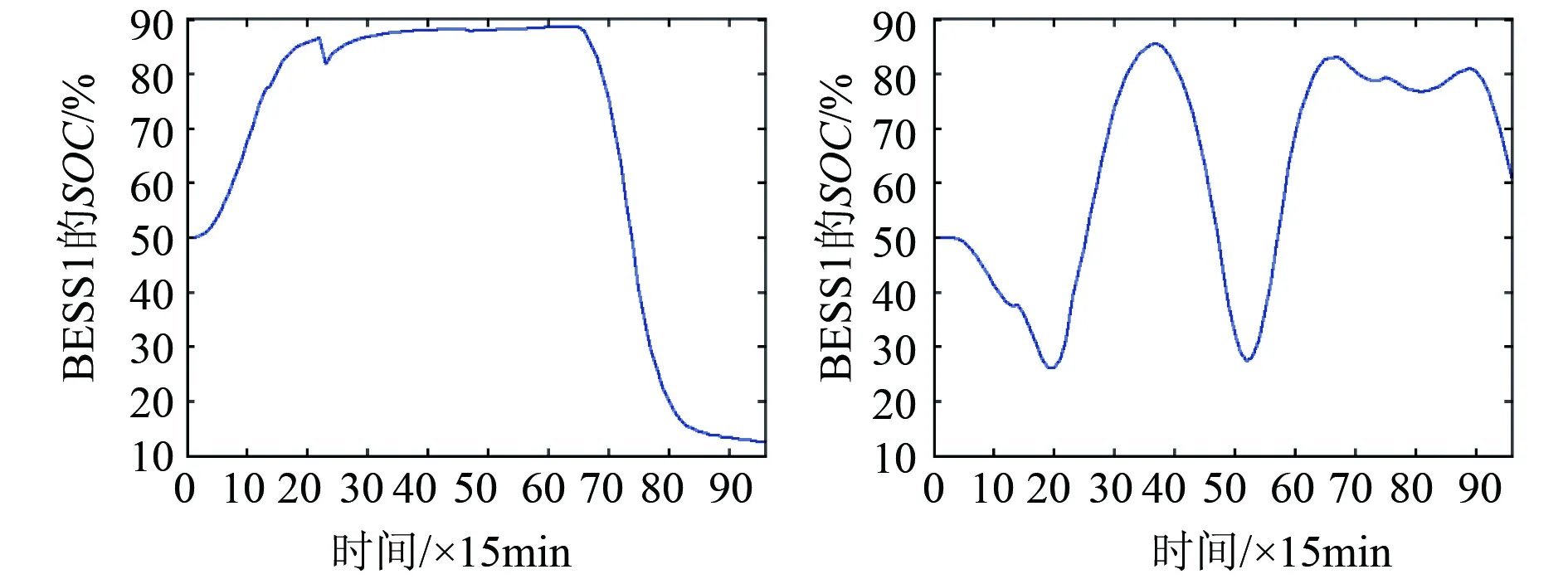
图16 协调控制时储能系统SOC变化情况

从图14看出，相对于孤立控制的储能系统而言，本节控制策略对配电网有功功率波动的平抑明显效果较好，可以减小配电网入口功率波动对电网的影响。从图15可以看出，在侧重优化功率波动的控制策略下，虽然节点8的电压波动相对于孤立控制的情形有所减小，但是节点2的电压波动却并未有明显优化。为了直观比较无储能、孤立控制和协调控制之间的差别，定义综合衡量电压波动的参数如下：

(11)

式中:SU为衡量节点2和节点8电压波动的综合指标；SU2为节点2电压的标准差，SU8为节点8电压的标准差。分别计算有功功率标准差SP，及SU2、SU8、SU如表3所示。

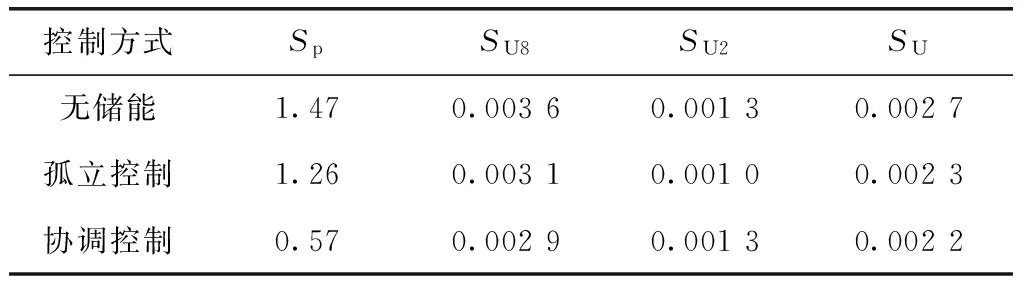
表3 3种控制方式效果对比

从表3可以看出，虽然协调控制策略并未使节点2电压的标准减小，但是对有功功率波动的平抑效果明显优于孤立控制，且综合衡量电压波动的指标SU也较小，表明本文控制策略具有较好的效果。本文算例分析考虑的是侧重于优化有功功率波动的控制目标，如果无储能接入时，配电网接入节点电压波动较大，则可以考虑在Pareto前沿中选择使节点电压波动目标函数较小的点或者折中解作为控制目标。

4 结束语

① 以配电网有功功率波动、新能源接入点电压波动为目标，建立了基于低通滤波的配电网多储能系统多目标协调控制优化模型，并且考虑了完整调度周期内储能系统的SOC约束，提出储能系统基于SOC反馈的控制策略，使SOC在一个完整调度周期内一直处在合理区间中。

② 使用NSGA-II算法对本文提出的多目标优化模型进行求解，可以获得优化模型的Pareto最优解集，根据优化目标的侧重点，在Pareto前沿上选择合适的解作为控制目标。

③ 对IEEE14节点配电网进行了算例分析，其中接入光伏6MWp，接入风电10MW。首先分析无储能时配电网有功功率波动和新能源接入节点电压波动，选择了优化功率波动作为优先控制目标，之后对无储能、储能孤立控制和储能协调控制3种情况的结果进行对比分析，表明了本文协调控制策略的有效性。

[1] 艾欣,董春发. 储能技术在新能源电力系统中的研究综述[J]. 现代电力,2015,32(5):1-9.

[2] 李建林,靳文涛,惠东,等. 大规模储能在可再生能源发电中典型应用及技术走向[J]. 电器与能效管理技术,2016,14:9-14.

[3] 胡荣,钟勇,符杨,等. 混合储能在配电网中的优化配置[J]. 现代电力,2015,32(3):49-53.

[4] 陶琼,桑丙玉,叶季蕾,等. 高光伏渗透率配电网中分布式储能系统的优化配置方法[J]. 高电压技术,2016(7):2158-2165.

[5] 吴小刚,刘宗歧,田立亭,等. 基于改进多目标粒子群算法的配电网储能选址定容[J]. 电网技术,2014,38(12):3405-3411.

[6] 尤毅,刘东,钟清,等. 主动配电网储能系统的多目标优化配置[J]. 电力系统自动化,2014,38(18):46-52.

[7] 赵金利,于莹莹,李鹏,等. 基于锥优化的储能系统参与配电网运行调节快速计算方法[J]. 电力系统自动化,2016,39(2):30-35,48.

[8] 章美丹,宋晓喆,辛焕海,等. 计及网损的配电网电池储能站优化运行策略[J]. 电网技术,2013,37(8):2123-2128.

[9] Antunes C H, Pires D F, Barrico C, et al. A multi-objective evolutionary algorithm for reactive power compensation in distribution networks[J]. Applied Energy, 2009, 86(7-8):977-984.

[10]Coello C A C, Pulido G T, Lechuga M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3):256-279.

[11]Ramirez-Rosado I J, Dominguez-Navarro J A. New multiobjective tabu search algorithm for fuzzy optimal planning of power distribution systems[J]. IEEE Transactions on Power Systems, 2006,21(1):224-233.

[12]熊超,马瑞. 考虑降损和平抑峰谷的配电网储能电池Pareto优化模型[J]. 电力建设,2015,36(8):34-40.

[13]孙伟卿,王承民,张焰,等. 基于Pareto最优的电力系统有功—无功综合优化[J]. 电力系统自动化,2009,33(10):38-42.

[14]阴皓. 基于云计算和改进NSGA-II的无功优化算法研究[D].北京：华北电力大学,2015.

[15]陈婕,熊盛武,林婉如. NSGA-II算法的改进策略研究[J]. 计算机工程与应用,2011(19):42-45.