有向图中网络Euler-Lagrange系统无需相对速度信息的群一致性

曹然 梅杰

在过去10多年里,关于多智能体系统的协同控制问题受到了国内外的广泛关注,例如编队问题[1]、聚集问题[2]、一致性问题[3]等.系统的一致性要求系统内所有智能体收敛于同一值.而在实际中,面对复杂任务时,常常需要系统的各部分分工合作,这就常常要求不同的部分收敛于不同值.群一致性问题将系统中的所有智能体分为几组,并要求同一组的所有智能体收敛于同一值,而组与组之间则可以不同,这使得群一致性在处理一些复杂问题时更加适用.

在系统动力学模型采用线性常微分方程以及拓扑结构为无向图的情况下,Wu等[4]使用牵制控制法[5]设计线性负反馈控制器使得系统实现群一致性,在此方法下实现群一致需要组间连接强度足够大.Xu等[6]使用牵制控制法设计分布式自适应控制器,并在假设拓扑图的Laplacian矩阵中的每个子块均行和列和为零的情况下实现了群一致性.基于有向拓扑结构,Xia和Cao[7]给出了三种情况下实现群一致性的条件:1)采用的动态模型不同;2)连接存在时滞因素影响;3)组与组之间存在竞争关系.与使用牵制控制法的情况类似的是这两种方法均需要可以得到系统的精确解,故对于强非线性的Euler-Lagrange系统不能直接使用.在Yu等[8]提出的入度平衡条件前提下,Qin等[9]放宽了实现群一致性的代数条件,并提出了分组时无环分割的概念,设计了分布式反馈控制器使得不同组的智能体最终收敛于不同的轨迹.Wen等[10]在智能体被分为两组且它们的动力学分别为一阶和二阶积分器的情况下,设计了一种使用邻居信息的分布式控制器,给出了在固定拓扑和切换拓扑下实现群一致性的充分条件.另外一些研究采用的多智能体系统的动力学是Euler-Lagrange方程,该系统在实际中有着大量的应用[11],例如无人机、工业机器人、走路机器人等.因此,网络Euler-Lagrange系统中的分布式协调控制也引起了广泛关注.研究内容包括一致性问题[12−13]、跟踪问题[14−15]、包含控制问题[16−17]等.在关于此类系统群一致性方面的现有研究中,Hu等[18]从两个组的情况出发,设计了控制器使得系统在固定拓扑和切换拓扑的结构下分别实现了群一致性,并推广到多个组的情况,然而其提出的代数条件较难实现.Liu等[19−20]运用了一种新的分解方法来得到Laplacian矩阵的特殊形式,并结合输入状态稳定来解决群一致性问题.在上述的研究中,所设计的控制器均使用了相对速度信息,而实际中相对速度信息较难精确得到.

结合之前的研究结果,本文在拓扑结构为有向图的情形下研究网络Euler-Lagrange系统的群一致性,组的分割方式与文献[9],文献[19−20]中普遍采用的无环分割方式相同,设计了无需相对速度信息的分布式算法,并在最后给出了仿真模拟来验证研究结论.

与文献[4−10]中考虑的线性多智能体动力学相比,本文采用的动力学模型是非线性的Euler-Lagrange方程. 与文献 [18−20]中研究的网络Euler-Lagrange系统群一致性相比,本文考虑到智能体间相对速度信息难以直接测量的实际情形,提出了无需相对速度信息的群一致性算法.与文献[13,17,21]中研究的网络Euler-Lagrange系统的一致性相比,本文研究的是系统的群一致性问题.在文献[21]中,智能体间信息传输权重均为正,而本文中不同组间智能体的信息传输权重可正可负.上述特点导致文献[21]中Lii,i=2,···,d,均为非奇异的M–矩阵,而在本文中,由入度平衡条件可知,Lii,i=2,···,d,均含有零特征值.这使得本文中的证明过程也与文献[22]不同.

1 数学背景与问题描述

在本文中,智能体采用的动力学模型是Euler-Lagrange方程

其中,qi∈Rp是广义坐标向量,Mi(qi)∈Rp×p是对称正定惯量矩阵,是Corios力和偏心力,gi(qi)为广义有势力,τi∈Rp表示作用在第i个智能体上的广义控制力.每个智能体的动力学模型有以下三个性质[23]:

性质 1.有界性:对于任意i,存在正常数使得

性质2.反对称性:是反对称的.

性质3.参数线性化:对于任意向量x,y∈Rp都成立,这里是回归矩阵,是智能体i的常值未知参数.

假设有n个智能体,智能体间的拓扑关系用有向图G=(V,E,A)表示[24].其中V={1,2,···,n}表示图中所有顶点组成的点集.E⊆V×V表示图中所有边组成的集合,一条边(i,j)∈E表示智能体j可以从智能体i中单向获得信息,我们称点j是点i的父节点,点i是点j的子节点.A=[aij]∈Rn×n表示图的带权邻接矩阵,当(j,i)∈E时有aij＞0,否则aij=0.一般我们假设一个节点不能连接自身,即aii=0.图G的Laplacian矩阵LA=[lij]∈Rn×n被定义为且有lij=−aij,i/=j.在有向图中,一条有向路径是一个边序列(i1,i2),(i2,i3),···,(ik−1,ik),其中任意一条边(im,im+1)∈E.如果至少存在一个节点(称为根节点),其到任意其他节点都有有向路径,则称该有向图具有有向生成树.如果一个图中任意两个不同节点间都存在一条有向路径,则称这个图是强连通的.如果一个有向图无法从任意节点出发经过若干条边回到该点,则称这个图是一个有向无环图.对有向图的Laplacian矩阵,有如下结论:

引理 1[25−26].G是一个n阶的有向图,LA∈Rn×n是与其对应的Laplacian矩阵.有以下两点成立:

1)如果有向图G包含一个有向生成树,则其Laplacian矩阵LA有一个单零特征值并且其余特征值均拥有正实部.

2)如果有向图G是强连通的,那么存在一个向量ξ=[ξ1,···,ξn]T∈Rn,其中,0,对于∀i=1,···,n,则有ξTLA=0成立.

引理2[22].G是一个n阶的有向图且是强连通的.定义矩阵其中Ξ=diag{ξ1,···,ξn},其中ξi如引理1中定义所示.则B是一个无向图的对称Laplacian矩阵.对任意向量ς∈Rn,有如下的不等式成立

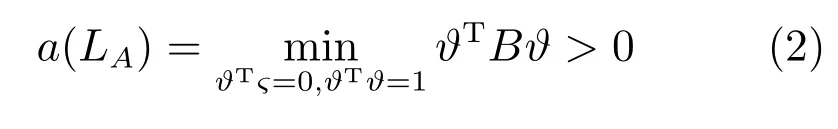
本文中所有智能体被分成d个组,如果将每个组视为一个点,其所构成的图G是有向无环图,我们则称原图G是可以无环分割的.{V1,V2,···,Vd}是点集V={1,2,···,n}的无环分割,其中Vi表示包含ni个点的一个组且有以及分属不同组的两个节点间可以存在竞争关系即aij＜0或合作关系即aij＞0,其中i∈Vk1,j∈Vk2,k1/=k2.

这里有如下结论:

引理3[18].对于任意可以无环分割的有向图G,假设其无环分割后的点集为{V1,V2,···,Vd},那么可以通过重新对所有顶点标号,使得G的Laplacian矩阵有如下的形式

其中,Lii为与Gi相关的矩阵,Lij表示从Gj到Gi的信息传输,i,j=1,2,···,d.

这里我们给出群一致性的定义:

定义 1.我们称被分成d个组的n个智能体在控制器τi的控制作用下可以实现群一致性当且仅当所有智能体的状态满足

注1.由定义1可知,本文的群一致性要求组内各智能体的状态都达到一致,而组与组之间各智能体的状态则可以不同.

2 控制律设计

在本文中,我们有如下假设:

假设1.图G是一个可以无环分割的有向图.

假设2.每一个组Vi对应的子图Gi都是强连通的.

假设3.组与组之间满足入度平衡条件[8],即对于任意两个不同组Gm与Gn有:

注2.具体地,假设1首先由Qin和Yu[9]在解决有向图下一般线性多智能体系统的群一致性问题中提出,是对系统内智能体进行分组的一个前提条件.假设2用来保证组内智能体能达到一致性.假设3则可以保证系统达到群一致性之后组外智能体的状态不对组内智能体的状态产生影响.在假设1下,不失一般性,可以将图G的Laplacian矩阵写成式(3)的形式.假设2是研究一致性问题中的常有要求,也是引理1和引理2的前提条件.根据假设3,当一个组达到平衡时,其接收到的其他组的信息输入总和为零,从而可以保持平衡状态.结合假设1和假设3以及引理3,可以得到式(3)中每个Lij的行和为零,且Lii为Gi对应的Laplacian矩阵.

首先,定义以下辅助变量[17,21]

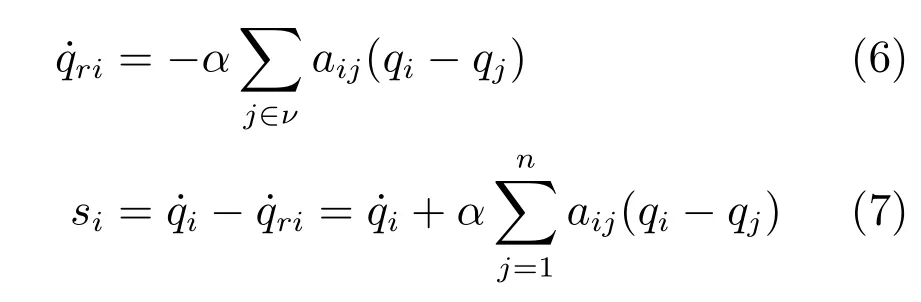
其中,α是一个正常数,aij代表邻接矩阵A的第i行第j列元素.

不使用智能体间的相对速度信息,设计如下所示的分布式自适应控制算法

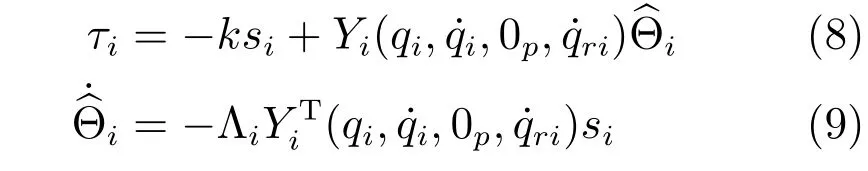
其中,k是一个正常数,是未知参数Θi的估计值, Λi是对称正定矩阵,如性质3中定义所示.定义将式(8)代入系统式(1)中可得

为了之后的收敛性分析,这里介绍一个特殊的(n−1)×n矩阵Q[27].

引理4[28].如果有向图G具有有向生成树,那么矩阵的特征值均有正实部,这里LA是图G的Laplacian矩阵.

显然在假设2的情况下,对于每一个子图Gi,都有对应的矩阵Qi.

对于多Lagrange系统的群一致性,有如下结论.

定理1.在假设1∼3成立的情况下,将控制算法(8)作用于系统(1),选择适当的控制增益k,系统将最终达到群一致性.

证明.首先考虑第1组的一致性问题.由假设2和式(3)可知,L11对应的子图G1是强连通的.那么由引理1可知,存在ξ1i＞0,i=1,···,n1,使得其中ζ1为ξ1i的列堆栈向量.定义参考向量d.令令X为qi的列堆栈向量,i=1,···,n.并有其中Xj为第j组所有智能体的状态变量的列堆栈向量,j=1,···,d.令为的列堆栈向量,i=1,···,n1.

选择如下的Lyapunov方程:

定义M(X1)=diag{M1(q1),···,Mn1(qn1)}, Ξ1=diag{ξ11,···,ξ1n1}.令S1和Xr1为si和qri的列堆栈向量,i=1,···,n1.由式(6)和式(7)可以得到

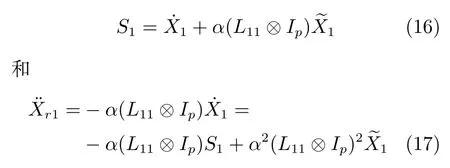
对式(15)求导,并考虑式(10)和性质2,可以得到

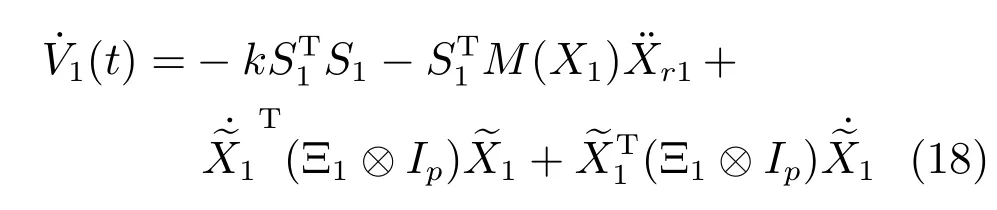
对于向量x,y以及恰当维数的矩阵P,有xTPy≤σmax(P)‖x‖‖y‖.根据此不等式,可以得到

注意到有

将式(20)和式(21)代入式(18)中可得

其中,B1=Ξ1L11+LT11Ξ1.注意到有(ζT1⊗Ip)=0p且子图G1是强连通的,根据引理2,有

将式(19),(23),(24)代入式(22)可得

显然,如果选择

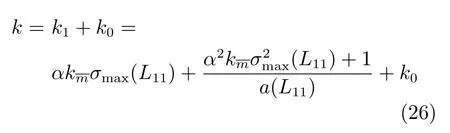
其中,k0是一个正常数,那么可以得到

接下来考虑第2组的一致性问题.由假设3可知,L22的行和为零,那么L22为子图G2的Laplacian矩阵.由假设2和引理1可知,存在ξ2i＞0,使得其中ζ2为ξ2i的列堆栈向量.与前文类似,选择如下的Lyapunov方程:

定义 Ξ2=diag{ξ21,···,ξ2n2},M(X2)= diag{Mn1+1(qn1+1),···,Mn1+n2(qn1+n2)}. 令S2,和qri的列堆栈向量,i=n1+1,···,n1+n2.由式(6)和式(7)可以得到

对式(28)求导,并考虑式(10)和性质2,可以得到

仿照第1组中情况,有

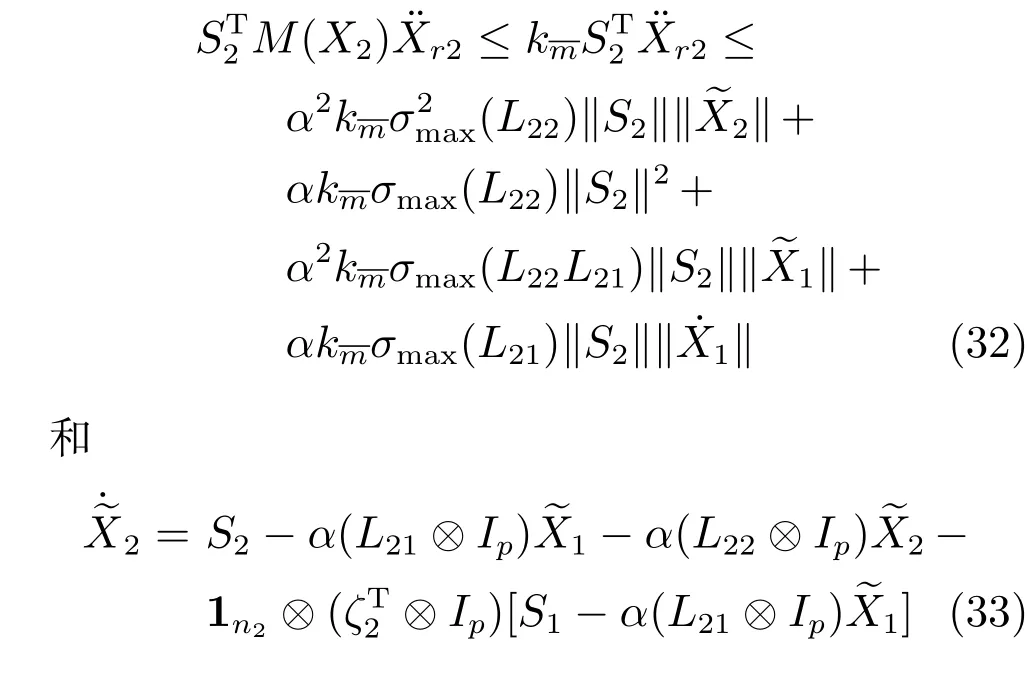
将式(32)和式(33),式(29)代入式(31)可得

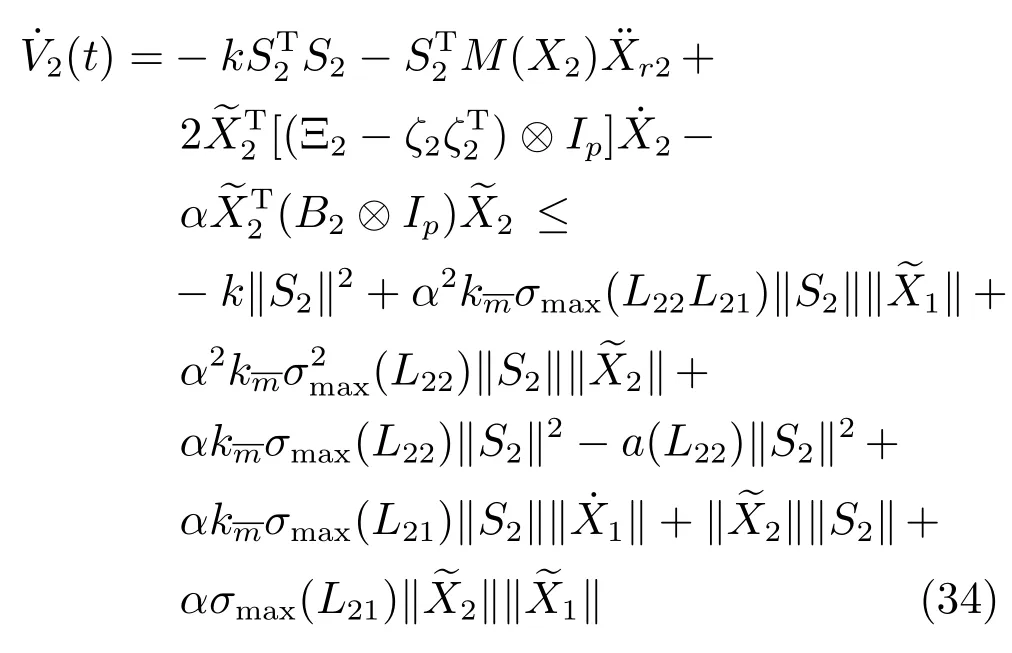
其中,B2=Ξ2L22+LT22Ξ2.注意到有

选择k=k2+k0,可以得到

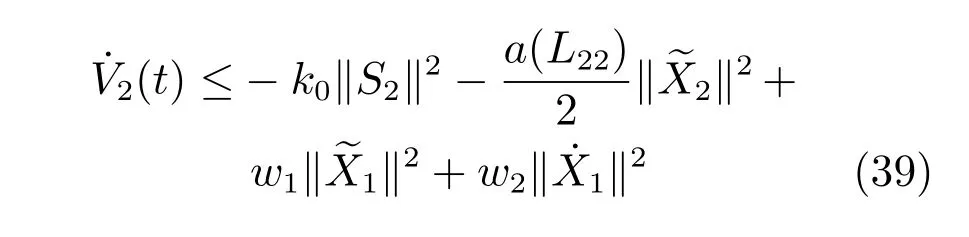
在式(39)两边同时积分可得

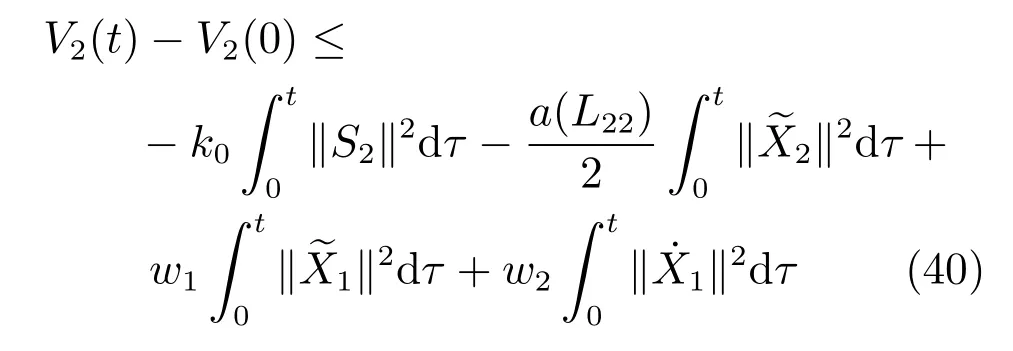
类似于前两组的情况,对于任意第i组智能体,当

令S为si的列堆栈向量,i=1,···,n.令注意此时的仍然满足式(12)和式(13),而由式(14)可知定义其中X已在证明开始时给出定义.

由式(7)可得

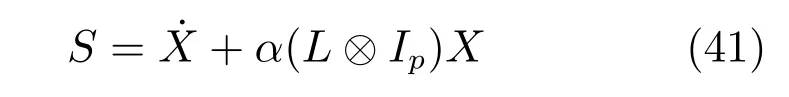
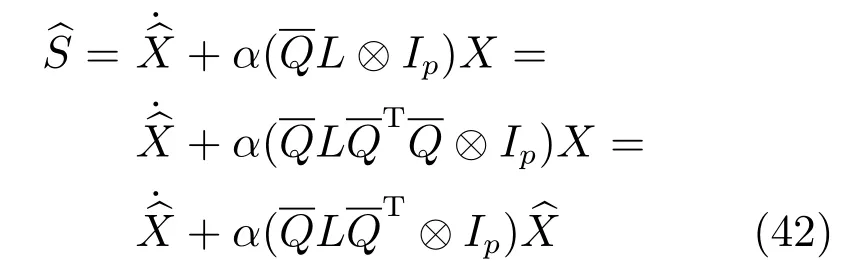
3 仿真分析

本节通过仿真验证设计的控制算法的有效性.

考虑5个二连杆转动机械臂所组成的系统,所有机械臂的动力学均为相同的Euler-Lagrange方程,关于方程的具体形式可参考文献[30].在仿真实验中,所采用的二连杆机械臂的各杆质量分别为m1=2.5kg和m2=1.8kg,各杆长度分别为l1= 1.0m和l2=0.6m,各杆连接点到质心的距离分别为lc1=0.5m和lc2=0.3m,各杆转动惯量分别为J1=0.2083kg·m2和J2=0.0540kg·m2,重力加速度为g=9.8m/s2.

各智能体的初始转动角度分别为[−2.0,1.0]T, [0.0,1.5]T,[1.0,2.0]T,[−1.0,−1.0]T,[0.0,−2.5]T,初始转动角速度分别为 [−1.25,0.25]T,[−0.25 0.75]T,[3.00,2.00]T,[−2.50,−0.75]T,[0.00,−1.50]T.控制参数我们选择k=8,α=1,Λi=5,∀i=1,···,5.

智能体间的拓扑关系如图1所示,机械臂的转角变化如图2所示,转动角速度变化如图3所示.可以看出两组智能体在所设计的控制算法的作用下,分别收敛于两个不同值,实现了群一致性的要求.

图1 智能体间的拓扑关系Fig.1 The networked topology associated with the agents

图2 有向拓扑图下智能体位置状态信息Fig.2 The position state of agents under the directed interaction graph

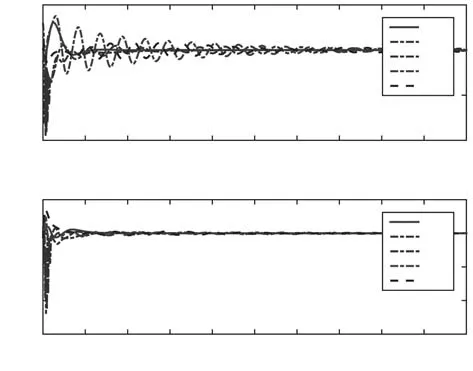
图3 有向拓扑图下智能体速度信息Fig.3 The velocities of agents under the directed interaction graph

4 结论

本文主要研究了当系统拓扑结构为有向图时网络Euler-Lagrange系统的群一致性问题.在系统参数不确定时,通过引入辅助变量构建状态方程,设计了无需相对速度信息的分布式自适应控制律,从而避免了实际中相对速度信息精度难以保证的情形.在所设计的控制律的控制作用下,系统中每一组的智能体的状态信息均可以收敛于同一点,而组与组之间的收敛点可以不同,从而实现了群一致性.最后通过仿真验证了所提算法的有效性.

1 Oh K K,Park M C,Ahn H S.A survey of multi-agent formation control.Automatica,2015,53:424−440

2 Su H S,Wang X F,Lin Z L.Flocking of multi-agents with a virtual leader.IEEE Transactions on Automatic Control, 2009,54(2):293−307

3 Yu H,Xia X H.Adaptive consensus of multi-agents in networks with jointly connected topologies.Automatica,2012, 48(8):1783−1790

4 Wu W,Zhou W J,Chen T P.Cluster synchronization of linearly coupled complex networks under pinning control.IEEE Transactions on Circuits and Systems I:Regular Papers,2009,56(4):829−839

5 Chen T P,Liu X W,Lu W L.Pinning complex networks by a single controller.IEEE Transactions on Circuits and Systems I:Regular Papers,2007,54(6):1317−1326

6 Xu C J,Zheng Y,Su H S,Chen M Z Q,Zhang C F.Cluster consensus for second-order mobile multi-agent systems via distributed adaptive pinning control under directed topology.Nonlinear Dynamics,2016,83(4):1975−1985.

7 Xia W G,Cao M.Clustering in diあusively coupled networks.Automatica,2011,47(11):2395−2405

8 Yu J Y,Wang L.Group consensus in multi-agent systems with switching topologies and communication delays.Systems and Control Letters,2010,59(6):340−348

9 Qin J H,Yu C B.Cluster consensus control of generic linear multi-agent systems under directed topology with acyclic partition.Automatica,2013,49(9):2898−2905

10 Wen G G,Huang J,Wang C Y,Chen Z,Peng Z X.Group consensus control for heterogeneous multi-agent systems with fi xed and switching topologies.International Journal of Control,2016,89(2):259−269

11 Min Hai-Bo,Liu Yuan,Wang Shi-Cheng,Sun Fu-Chun.An overview on coordination control problem of multi-agent system.Acta Automatica Sinica,2012,3810:1557−1570 (闵海波,刘源,王仕成,孙富春.多个体协调控制问题综述.自动化学报,2012,38(10):1557−1570)

12 Cheng L,Hou Z G,Tan M.Decentralized adaptive consensus control for multi-manipulator system with uncertain dynamics.In:Proceedings of the 2008 IEEE International Conference on Systems,Man,and Cybernetics.Singapore: IEEE,2008.2712−2717

13 Ren W.Distributed leaderless consensus algorithms for networked Euler-Lagrange systems.International Journal of Control,2009,82(11):2137−2149

14 Mei Jie,Zhang Hai-Bo,Ma Guang-Fu.Adaptive coordinated tracking for networked Euler-Lagrange systems under a directed graph.Acta Automatica Sinica,2011,375:596−603 (梅杰,张海博,马广富.有向图中网络Euler-Lagrange系统的自适应协调跟踪.自动化学报,2011,37(5):596−603)

15 Mei J,Ren W,Ma G F.Distributed coordinated tracking with a dynamic leader for multiple Euler-Lagrange systems.IEEE Transactions on Automatic Control,2011,56(6): 1415−1421

16 Meng Z Y,Ren W,You Z.Distributed fi nite-time attitude containment control for multiple rigid bodies.Automatica, 2010,46(12):2092−2099

17 Mei J,Ren W,Ma G F.Distributed containment control for Lagrangian networks with parametric uncertainties under a directed graph.Automatica,2012,48(4):653−659

18 Hu H X,Zhang Z,Yu L,Yu W W,Xie G M.Group consensus for multiple networked Euler-Lagrange systems with parametric uncertainties.Journal of Systems Science and Complexity,2014,27(4):632−649

19 Liu J,Xiang L,Zhao L Y,Zhou J.Group consensus in uncertain networked Euler-Lagrange systems with acyclic interaction topology.In:Proceedings of the 34th Chinese Control Conference.Hangzhou,China:IEEE,2015.835−840

20 Liu J,Ji J C,Zhou J,Xiang L,Zhao L Y.Adaptive group consensus in uncertain networked Euler-Lagrange systems under directed topology.Nonlinear Dynamics,2015,82(3): 1145−1157

21 Mei J,Ren W,Chen J,Ma G F.Distributed adaptive coordination for multiple Lagrangian systems under a directed graph without using neighbors′velocity information.Automatica,2013,49(6):1723−1731

22 Mei J,Ren W,Chen J.Distributed consensus of secondorder multi-agent systems with heterogeneous unknown inertias and control gains under a directed graph.IEEE Transactions on Automatic Control,2016,61(8):2019−2034

23 Spong M W,Hutchinson S,Vidyasagar M.Robot Modeling and Control.New Jersey,USA:John Wiley and Sons,2006.

24 Mesbahi M,Egerstedt M.Graph Theoretic Methods in Multiagent Networks.New Jersey,USA:Princeton University Press,2010.

25 Ren W,Beard R W.Distributed Consensus in Multi-Vehicle Cooperative Control.London,Britain: Springer-Verlag, 2008.

26 Yu W W,Chen G R,Gao M,Kurths J.Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics.IEEE Transactions on Systems,Man,and Cybernetics,Part B(Cybernetics),2010,40(3):881−891

27 Scardovi L,Arcak M,Sontag E D.Synchronization of interconnected systems with applications to biochemical networks:an input-output approach.IEEE Transactions on Automatic Control,2010,55(6):1367−1379

28 Mei J.Weighted consensus for multiple Lagrangian systems under a directed graph.In:Proceedings of the 2015 Chinese Automation Congress(CAC).Wuhan,China:IEEE,2015. 1064−1068

29 Horn R A,Johnson C R.Matrix Analysis.New York,USA: Cambridge University Press,1985.

30 Kelly R,S´a˜ntibanez V,Lor´ıa A.Control of Robot Manipulators in Joint Space.London,Britain:Springer,2005.