几何画板是数学发现的望远镜*
——对观摩研讨课一道例题的课后探索
2018-03-09
●
(明港中学,浙江 宁波 315806)
最近,笔者参加了一次同课异构的观摩研讨课活动,两位教师都重点讲了同一道课本例题:
例1已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这边所对边长的一半.
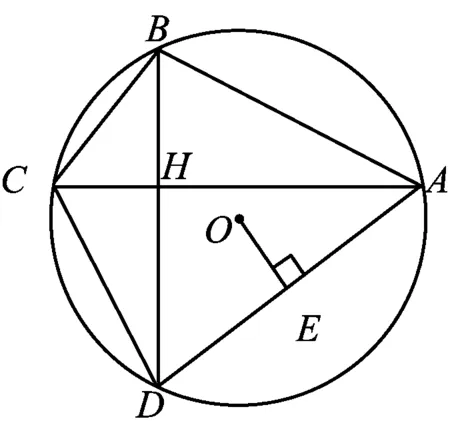
图1

两位教师教态自然,着眼于培养学生的数学核心素养,对比讲解笛卡尔的解析法和欧几里得的几何法,启发学生积极回答和变式练习.例1的教学片段是这两节同课异构的预设难点和实际亮点,赢得了听课教师的赞赏.
课后,我们对照两位教师的教案,运用几何画板动态演示例1的示意图,首先发现一个有关平行四边形的新猜想:
猜想1在图1的基础上,取BC的中点F(如图2所示),则顺次连接点O,F,H,E构成平行四边形.

图2 图3
复验以图2中直线CA,DB分别为x轴、y轴,建立如图3所示的直角坐标系xHy.设点A(a,0),B(0,b),C(c,0),D(0,d),则

从而
同理可得|OE|=|FH|.
要验证顺次连接点O,F,H,E构成平行四边形,|OF|=|EH|且|OE|=|FH|是必要条件,还要考虑点O,F,H,E不共线的特殊情形和点O,H不重合的退化情形.
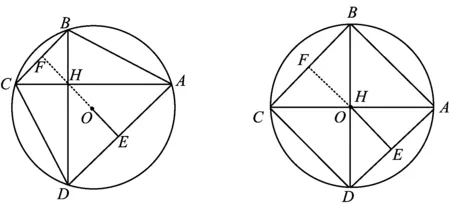
图4 图5
实际上,在已有的条件下,当|HA|=|HD|≠|HB|时,点O,F,H,E共线(如图4所示);当|HA|=|HB|=|HC|=|HD|时,点O与点H重合(如图5所示).总之,猜想1不正确.
猜想1虽然有差错,但复验过程所蕴含的正确因素是极其宝贵的,从中能够去伪存真地得到:

图6
定理1如图6,⊙O的内接四边形ABCD的两条对角线互相垂直,垂足H不重合于圆心O.
1)取边AD的中点E,取边BC的中点F,则当HA≠HD时,四边形OFHE是平行四边形;
2)取边AB的中点M,取边CD的中点N,则当HA≠HB时,四边形ONHM是平行四边形.
圆经过压缩变换就变成了椭圆,其中的两条直线平行保持不变性,多点共线保持不变性,线段中点保持不变性,于是就容易顿悟到:
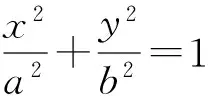
演示1运用几何画板可检验度量:
|OE|=|FH|, |OF|=|EH|,
|OM|=|NH|, |ON|=|MH|.
如图7所示,符合结论.

图7
演示2运用几何画板,依次选点O,E通过变换窗口标记向量,再把点F通过变换窗口按标记向量平移,恰好重合于点H;依次选点O,M通过变换窗口标记向量,再把点N通过变换窗口按标记向量平移,恰好重合于点H.
证明依题意,设A(acosα,bsinα),B(acosβ,bsinβ),则H(acosβ,bsinα),C(-acosα,bsinα),D(acosβ,-bsinβ),可得

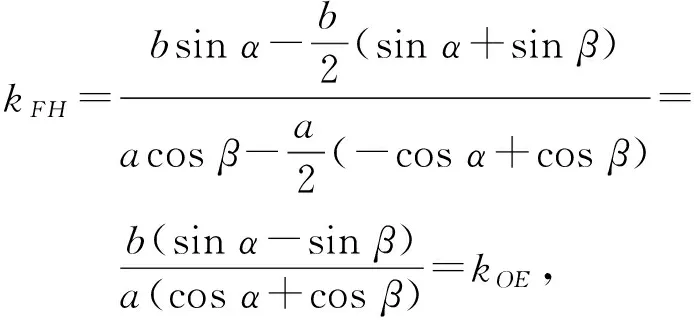
同理可证
kEH=kOF.
综上所述,当AD与BC不平行时,四边形OFHE是平行四边形;同理可证,当AB与CD不平行时,四边形ONHM是平行四边形.
补充说明1)在定理2的先决条件下,当AD∥BC时,点O,F,H,E共线;当AB∥CD时,点O,N,H,M共线.
2)经过几何画板的操作试验,假如将定理2中“两条弦AC,BD分别垂直于y轴、x轴”推广替换为“两条弦AC,BD互相垂直”,如图8所示,则相应结论错误.

图8 图9
3)经过几何画板的操作试验,假如将定理2中“两条弦AC,BD分别垂直于y轴、x轴,垂足H在椭圆内”类比替换为“两条弦AC,BD所在直线分别垂直于y轴、x轴,垂足H在椭圆外”,如图9所示,则相应结论仍然正确.
4)回眸定理1中的圆,可作类似于上述3)的几何画板操作试验(可用标记向量进行平移的快捷途径),也可得到相应正确结论(示意图略).
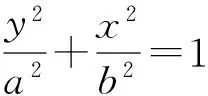


把定理3中的椭圆类比到双曲线中去思考,经过几何画板演示(如图10和图11)后,可得到一个类比结论:
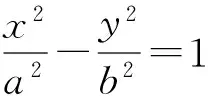

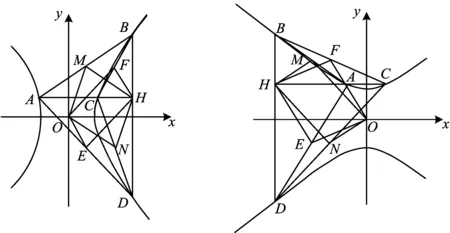
图10 图11
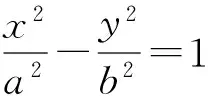
从而
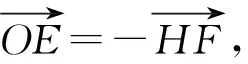
xE+xF=xH,
(1)
和yE+yF=yH.
(2)
事实上,
同理可得
yE+yF=yH.
于是,式(1)和式(2)成立,因此



提炼上述4个定理的共性,可以高度抽象出一个更加统一的大团圆结论:
定理5如果有心二次曲线Ω(圆或椭圆或双曲线)的两条弦AC,BD所在的直线分别垂直于该曲线Ω的两条互相垂直的对称轴,直线AC与直线BD的垂足H不在该曲线Ω上,取弦AD,BC,AB,CD的中点依次为E,F,M,N,那么有向量等式

补充说明在定理5中,假如直线AC与直线BD的垂足H在该曲线Ω上(前面的条件都不变),那么弦AC和弦BD必然各有一个端点都重合于垂足H,不妨设点C和点B都重合于点H,那么“极限化的中点”F也重合于垂足H,而中点E重合于曲线Ω的中心,于是借用零向量也可以使该定理结论的4个向量等式仍然成立.
上面层层递进的一串探索流程,既有对教材内涵的挖掘,又有对教法学法的指导,可以选作几何画板辅助探究性学习的课题设计.
笔者余兴未尽,最后谈两点启示:
启示1例1选自课本例题,平时我们对这道题熟视无睹,似乎没有挖掘价值,其实不然.如果我们平时能像展示课的例题教学那样对待课本的许多例习题,充分激活个体的创新潜质,充分营造群体的合作氛围,把外界激励自觉转化为内心驱动,进行匠心探索和细心品味,那么就可以发现许多数学新奥秘.
启示2在把一道例题逐步抽象升华为5个定理的探索过程中,几何画板的动态演示起到了不证先知的作用.美国数学史家克莱因说过:“数学的最大进步是由具有杰出的直觉能力的人所推动的,而不是由具有构造严格证明能力的人所推动的”.现在看来,几何画板可以促使我们的数学直觉能力显性化、快捷化,是我们一目了然地发现数学新奥秘的望远镜.
[1] 陈咸存.用几何画板探究、猜想与验证[J].数学通报,2016(4):26-28.
[2] 甘大旺.运用几何画板画圆锥曲线的三种方法[J].中学数学,2007(8):23-26.
