间歇式俯仰转动扑翼的自主推进
2018-03-09戴龙珍中国科学院力学研究所北京100190中国科学院大学工程科学学院北京100049
戴龙珍, 张 星,*(1. 中国科学院力学研究所, 北京 100190; 2. 中国科学院大学 工程科学学院, 北京 100049)
0 引 言
很多生物在飞行和游动中均采用主动驱动和被动滑行交替(flap-and-glide/burst-and-coast)的间歇式推进[1-9]。一些已有的研究表明,在移动同样距离的条件下,间歇式驱动的游动可以有效地节省能量消耗[2,3,6,10-15]。间歇式驱动的飞行与游动问题又可细分为两大子类,它们的节能机理也不尽相同。
第一类问题中动物的身体密度大于所处的流体介质(如鸟类和一些水生哺乳动物)。动物采用间歇式驱动和上下起伏的运动轨迹,可以有效地利用重力势能来增大水平移动的距离[1-2]。第二类问题中动物的身体密度和所处的流体介质接近(如某些鱼类)。这类间歇式驱动的节能机理则包括黏性和无黏两种。
黏性机理又称为Bone-Lighthill 边界层薄化假设,即主动游动比滑行时的边界层变薄,因此摩擦阻力更大[3-4,6,16]。无黏机理又称为Garrick机理,即间歇式驱动改变了产生推力的附加质量力与产生诱导阻力的环量力之比值[13]。
目前,绝大多数关于仿生扑翼推进的流体力学研究主要针对连续式的垂直振荡(plunging)和俯仰旋转 (pitching) 两种驱动方式。近期,一些学者受到生物间歇式驱动的启发,开始研究间歇式驱动扑翼的推进问题。Floryan 等[14]通过水槽实验,测量了不同占空比(duty cycle) 条件下间歇式俯仰旋转驱动扑翼的平均推力和平均输出功率。他们的研究表明,间歇式驱动普遍比连续式驱动在能效利用率方面占优。同时,他们还发现占空比的改变基本不影响一个完整驱动周期内产生的涡的位置与强度。Moored等[15]针对间歇式俯仰旋转驱动的扑翼推进问题,开展了无黏和有黏的数值模拟。无黏的数值模拟结果表明,在相同推进速度的条件下,间歇式驱动在能效方面占优。有黏的数值模拟结果表明,在一定的速度范围内,间歇式驱动在能效方面占优。上述实验和数值研究的主要目标是比较连续式和间歇时驱动的推进性能,对于间歇式驱动的流场结构研究较少,也缺少详细的描述。
本文通过Navier-Stokes方程和牛顿方程的耦合求解,开展连续式和间歇式俯仰旋转扑翼自主推进问题的有黏数值模拟。研究目标是考查一定雷诺数范围内间歇式驱动能否提高能效,同时对间歇式驱动和连续式驱动产生的流场结构进行对比分析。
1 计算模型
1.1 问题描述与控制方程
我们考虑一个俯仰旋转驱动薄板翼的自主推进问题。扑翼的弦长为L,旋转角度随时间的变化规律可以采用如下的分段函数描述(如图1所示):

(1)

(2)
其中θ0为转角幅值,f为扑动频率。Tcyc为一个包含主动扑动与被动滑行的完整周期,Tb=1/f为一个完整周期中主动扑动的时间,DC=Tb/Tcyc为占空比。Tr(t)为主动驱动和被动滑行之间的光滑过渡函数(为文献[15]中过渡函数的平方),其中m是过渡区长短的控制参数。

图1 俯仰旋转扑翼的自主推进问题Fig.1 Self-propulsion of a pitching foil
我们假设流动为二维层流。流动可以由如下无量纲形式的不可压缩Navier-Stokes方程描述:

(3)
(4)
其中u和p代表流体的速度和压力。本研究采用浸入边界方法求解流体方程,即通过引入适当的体积力源项f间接地实现扑翼表面的无滑移边界条件。因此,f同时代表了扑翼和流体间的相互作用力。无量纲化的参考长度、参考速度和参考时间分别为L、fL和1/f。雷诺数的定义为:Ref=fL2/ν,这里ν是流体的运动学黏性系数。
薄板翼可以在水平方向上自主推进(竖直方向的位移通过俯仰旋转指定)。薄板翼在水平方向的运动可以由如下无量纲形式的牛顿第二定律描述:

(5)
其中β=(ρsδ)/(ρfL)为质量比,这里ρs和ρf分别代表扑翼和流体的密度,δ为扑翼的厚度。Fx代表沿扑翼表面分布的(无量纲)拉格朗日力水平分量,Δs为拉格朗日网格的无量纲宽度(与求解流体方程欧拉网格的无量纲宽度相等)。在浸入边界方法中,沿物面分布的拉格朗日力与出现在流体动量方程中的体积力源项可以通过适当的插值方法相互转换。
1.2 计算方法与计算网格
我们采用直接加力的浸入边界方法处理运动边界,采用离散流函数方法求解不可压NS方程[17]。我们采用欧拉方法离散时间牛顿方程中的时间导数项,并且采用松耦合方法实现流体和动力学方程的耦合。我们在前期工作中,已经通过大量的标准算例,对该求解器进行了严格的验证[17-18]。
本研究采用多块拼接的直角坐标网格(如图2所示),以运动翼周围的矩形区域为网格最密的中心块,围绕它向外增加环形块;每增加一块,网格的几何尺寸加倍。该文中总计算区域为[-23L,23L]×[-6L,6L],网格总数为85万,一共用了5个块。其中,中心块所占区域为[-15L,15L]×[-L,L],网格尺寸为0.01L。
1.3 控制参数
为了在相同推进速度的条件下对比连续式驱动和间歇式驱动的推进效率。我们模拟了在基准频率f0驱动下,占空比为0.2-0.9的间歇式驱动的自主推进问题。同时,我们还模拟了0.3-0.9倍基准频率下连续式驱动(占空比为1.0)的自主推进问题。模拟采用的驱动频率和占空比如表1所示。数值模拟采用的其它参数(雷诺数、质量比、转角幅值和过渡区控制参数)如表2所示。

表2 模拟所用的其它控制参数Table 2 Other parameters used in the simulations
2 结果与讨论
2.1 瞬时推进速度
图3对比了连续式驱动(f=0.7f0)和间歇式驱动(DC=0.5)条件下(两者的平均推进速度相同),头部的水平速度随时间的变化规律。由图可见, 间歇式驱动的主动段存在两段加速和两段减速的复杂历程,完全不同于连续式驱动的简协振荡规律。间歇式驱动的滑行段是一个速度单调下降的减速段。

图3 一个周期内头部水平速度随时间的变化(左右分别对应f=0.7f0的连续式驱动和DC=0.5的间歇式驱动,T=1/f为连续性运动的周期)Fig.3 Horizontal velocity of the head as a function of time (left and right plots correspond to the continuous actuation with f=0.7 f0 and the intermittent actuation with DC=0.5 respectively)
2.2 水平力与侧向力
图4对比了连续式驱动(f=0.7f0)和间歇式驱动(DC=0.5)条件下(两者的平均推进速度相同),水平合力随时间的变化规律。如图可见,间歇式驱动产生的水平合力在主动段出现了三个波峰和两个波谷,完全偏离了连续式驱动对应的(近似)简协振荡规律。进入被动段后,水平合力表现为缓慢下降的阻力。
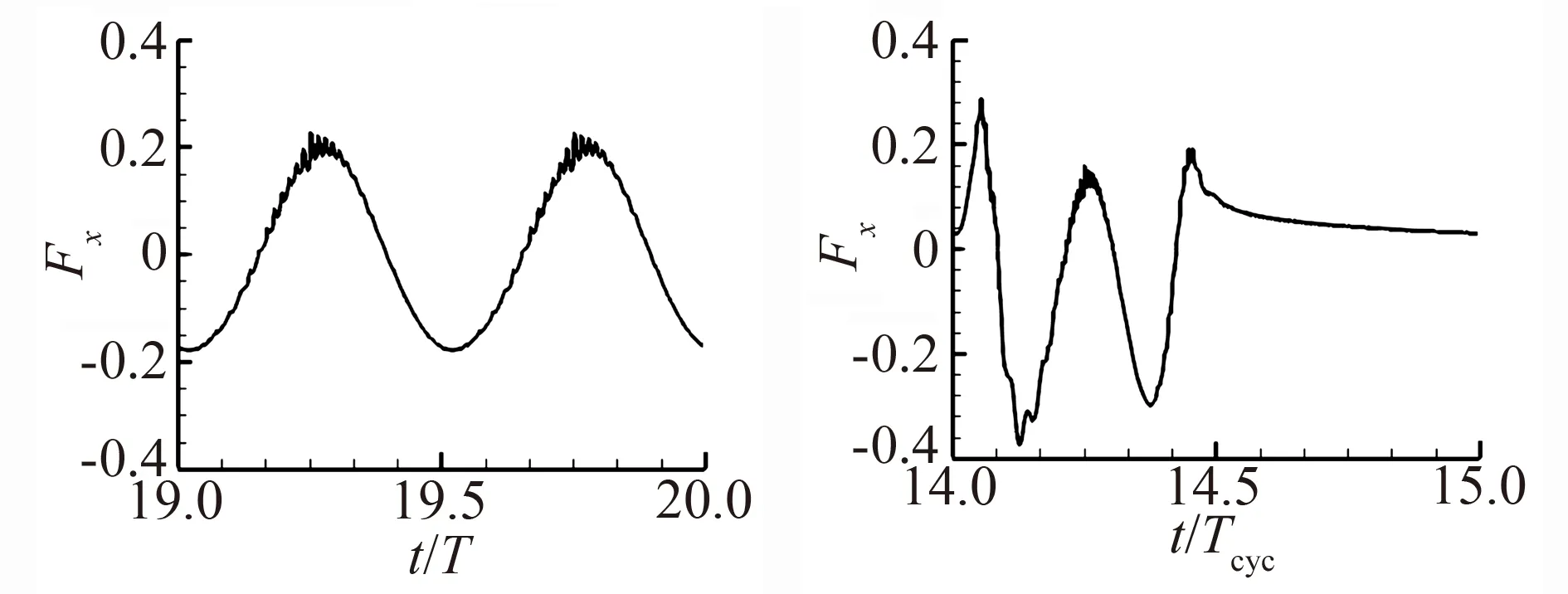
图4 一个周期内水平合力随时间的变化(左右分别对应连续式驱动f=0.7 f0和DC=0.5的间歇式驱动,T=1/f为连续性运动的周期)Fig.4 Resultant horizontal force as a function of time (left and right plots correspond to the continuous actuation with f=0.7 f0 and the intermittent actuation with DC=0.5 respectively)
图5对比了连续式驱动(f=0.7f0)和间歇式驱动(DC=0.5)条件下,侧向合力随时间的变化规律。间歇式驱动产生的侧向合力在主动段出现两个波峰和两个波谷,同样完全偏离了(近似)简谐振荡的规律。在进入被动段后,侧向合力出现了一段时间的高频振荡,然后才逐渐衰减到零。

图5 一个周期内侧向合力随时间的变化(左右分别对应连续式驱动f=0.7f0和DC=0.5的间歇式驱动,T=1/f为连续性运动的周期)Fig.5 Resultant lateral force as a function of time (left and right plots correspond to the continuous actuation with f=0.7 f0 and the intermittent actuation with DC=0.5 respectively)
2.3 运动能耗
我们首先定义两个衡量推进性能的重要指标,即平均推进速度和平均单位质量的输入功率:
(6)

(7)
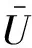
我们用单位质量单位距离的能耗(COT)来衡量推进效率,COT的定义为:

(8)

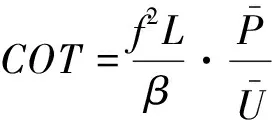
(9)
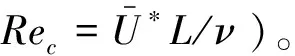
在Moored等的有黏数值模拟中,雷诺数的范围是2500至7500,比本文雷诺数大约高一个量级。他们观察到的COT随推进速度的变化规律和本文的结果在定性上基本一致[15]。

图6 COT随推进速度的变化Fig.6 Variation of COT with the cruising velocity
2.4 流场结构
连续式和间歇式推进得到的流场结构如图7所示,这里以推进速度定义的雷诺数为340(对应于图6中的COT趋势转变点)。
如图7所示,在连续式推进中,一个扑动周期内有两个涡从尾缘脱落。脱落的涡在尾迹中以反卡门涡街的形式水平排列。因此,流场的平均速度剖面可以保持上下对称。在间歇式推进中,一个完整的周期(括主动驱动和被动滑行)内有三个涡从尾缘脱落。其中,逆时针旋转的涡(红色代表的涡)由于涡之间的相互作用被撕裂为两部分,并且和顺时针旋转的涡(蓝色代表的涡)组成上下两排涡对。由于上面一排涡对的强度明显低于下面一排流场的,平均速度剖面上下对称性被打破。可以推断,间歇式驱动将会带来平均侧向力不为零的问题。这也是在仿生水下航行器的设计中需要考虑的问题。
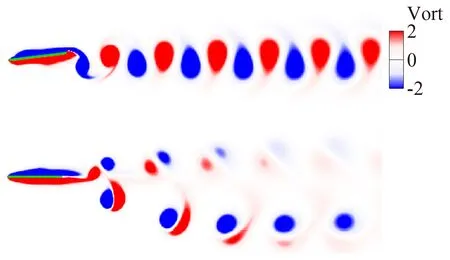
图7 连续式驱动(上)和间歇式驱动(下)的流场结构对比Fig.7 Comparison of the flow structures in continuous (upper) and intermittent (lower) propulsions
3 结 论
我们通过数值模拟研究了连续式和间歇式俯仰转动驱动的扑翼自主推进问题。研究表明,在同样推进速度的前提下,如果推进速度较低,连续式推进所需能耗较低;如果推进速度较高,则间歇式推进所需能耗较低。研究还发现,间歇式驱动产生的流场结构呈现明显的上下不对称性,因此会产生一定的平均侧向力。本研究得到的结果对于仿生水下航行器的设计有一定的参考价值。
致谢:感谢国家超级计算天津中心提供的计算机机时。
[1]Haury L, Weihs D. Energetically efficient swimming behavior of negatively buoyant zooplankton[J]. Limnology and Oceanography, 1976, 21(6): 797-803
[2]Gleiss A C, Jorgensen, S J, Liebsch N, et al. Convergent evolution in locomotory patterns of flying and swimming animals[J]. Nature Communications, 2011, 2(1): 2555-2559
[3]Weihs D. Energetic advantages of burst swimming of fish[J]. Jounal of Theoretical Biology, 1974, 48(1): 215-229
[4]Weihs D. Energetic significance of changes in swimming modes during growth of larval anchovy[J]. Fishery Bulletin, 1980, 77(3): 597-604
[5]Videler J J. Swimming movements, body structure and propulsion in cod Gadus morhua[J]. Symposia of the Zoological Society of London, 1981, 48: 1-27
[6]Videler J J, Weihs D. Energetic advantages of burst-and-coast swimming of fish at high speeds[J]. Journal of Experimental Biology, 1982, 97(4): 169-178
[7]Blake R W. Functional design and burst-and-coast swimming in fishes[J]. Canadian Journal of Zoology, 1983, 61(11): 2491-2494
[8]Muller U K, Stamhuis E J, Videler J J. Hydrodynamics of unsteady fish swimming and the effect of body size: comparing the flow fields of fish larvae and adults[J]. Journal of Experimental Biology, 2000, 203(2): 193-206
[9]Fish F E, Fegely J F, Xanthopoulos C J. Burst-and-coast swimming in schooling fish (Notemigonus Crysoleucas) with implications for energy economy[J]. Comparative Biochemistry & Physiology Part A Physiology, 1991, 100(3): 633-637
[10]Wu G H, Yang Y, Zeng L J. Kinematics, hydrodynamics and energetic advantages of burst-and-coast swimming of koi carps (Cyprinus carpio koi)[J]. Journal of Experimental Biology, 2007, 210(12): 2181-2191
[11]Yang Y, Wu G H, Yu Y L, et al. A study on flow physics of burst-and-coast swimming of koi carp (Cyprinus carpio koi) based on measurements and numerical simulations[J]. Journal of Aero Aqua Bio-mechanisms, 2010, 1(1): 30-38
[12]Chung M H. On burst-and-coast swimming performance in fish-like locomotion[J]. Bioinspiration & Biomimetics, 2009, 4(3): 036001
[13]Akoz E, Moored K W. Unsteady propulsion by an intermittent swimming gait[J]. Journal of Fluid Mechanics, 2018, 834: 149-172
[14]Floryan D, Van Buren T, Smits A J. Forces and energetics of intermittent swimming[J]. Acta Mechanica Sinica, 2017, 33(4): 725-732
[15]Moored K, Akoz E, Liu G, et al. Disentangling the inviscid and viscous energy saving mechanisms of intermittent swimming[C]//47th AIAA Fluid Dynamics Conference, 2017
[16]Lighthilll M J. Large-amplitude elongated-body theory of fish locomotion[J]. Proceedings of the Royal Society of London B: Biological Sciences, 1971, 179(1005): 125-138
[17]Wang S Z, Zhang X. An immersed boundary method based on discrete stream function formulation for two- and three-dimensional incompressible flows[J]. Journal of Computational Physics, 2011, 230: 3479-99
[18]Zhu X J, He G W, Zhang X. Numerical study on hydrodynamic effect of flexibility in a self-propelled plunging foil[J]. Computers & Fluids, 2014, 97(6): 1-20.
