城市路网交通流的数学模型及仿真
2018-03-08钟建新王照生
钟建新,王照生
(赣州师范高等专科学校,江西 赣州 341000)
社会经济的发展和城市化水平的不断提高,对城市交通提出了越来越高的要求。目前,城市交通拥挤和交通事故频发严重地困扰着交通管理部门和出行者,解决这些问题成为缓解城市交通压力的迫切需要,也是加快城市化进程需要研究的一个重要课题。近年来,电子通信技术的飞速发展及智能运输系统的产生得到世界各国的普遍关注,借助这些技术,开发城市汽车导航系统,实现路网信息的集成与共享,对改善路网拥挤与提高道路通行能力卓有成效。
目前,全球定位技术和双向信息传递技术已经趋向成熟,只需进行相应的改进和有机结合,就可以实现车辆定位和各种信息的传送和转化。因此,在汽车导航系统中,尚未解决的是导航依据和方法问题,即为用户选择怎样的出行路径才能满足用户的不同出行目的和需要,并且达到避免拥挤、提高整个路网使用效率的目的。如何在短时间内获取路网和用户信息,以及如何根据这些信息快速确定出最优出行路径。这是运输领域的一个前沿理论问题,即“动态路径选择”问题,其优劣将直接影响汽车导航系统进而整个系统的造价和功能。
近年来,世界各国在这个领域进行了深入地研究,取得了比较可观的成果,但所建模型普遍存在着约束条件苛刻、计算量大、优化时间长等问题。最早的分配模型是以起讫点间路径的长短来选择最短路径的,这种方法显然不符合复杂多变的城市交通流,传统的动态分配模型是根据已知路网系统的OD交通量预测出各路段的交通流量,这种模型也不能解决交通流随时可能发生变化这一问题实际;路径选择问题是一个NP难问题,随着求解问题规模的扩大,现有的智能算法,例如蚁群算法在求解这类问题的时候,难免会碰到陷入局部最优解和收敛速度慢的问题。因此,现有的求解模型和算法都难以满足实际汽车导航的需要,而蜂群智能算法因为其快速的收敛速度很适合用来解决这类问题。基于这点,本文提出了一种城市道路汽车导航算法,建立了城市汽车导航系统路径选择分配模型,并且采用蜂群智能算法求解了该模型,仿真结果表明了算法的有效性和实用性。
一、城市汽车导航路径选择模型
(一)汽车导航系统控制影响因素分析
城市交通流复杂多变,交通密度差别很大,以路径长短为唯一参变量进行研究具有很大的局限性。因此,具有实际应用价值的汽车导航系统必须综合考虑复杂的交通影响因素。出行者根据道路交通实时情况,会对出行时间和出行路线进行调整,以减少路上时间的消耗;起讫点间的最优路径将随着交通流的实时变化而发生改变;高峰时段的交通流造成的交通拥堵在时空上具有不稳定性。通过大量的文献研究和调查,影响城市出行者出行时间的最主要因素不是路径的长短,而是起讫点间各路段的综合通行能力。本文为了便于研究又不失一般性,选取两个最主要的影响因素,即路径长短和交通拥挤程度进行对比研究,给出模型并进行仿真,得到了比较满意的结果。
(二)模型建立
城市交通流状况错综复杂,并且始终都在变化。出行车辆根据出发时刻动态交通网络各条边的权值来计算从第一个节点到终点的最佳路径,到达第二个节点前,交通网络里的各条边的权值随时间和交通流信息而发生了变化,相应地,出行车辆的最优路径也会发生变化,因此,出行车辆在此时此刻以第二个节点为起点,重新组合优化网络,来计算从该节点到终点的最佳路径,以决定车辆到达第二个节点时应该向哪一条道路转向,以此类推,在这种情况下,车辆到达终点时遍历的路径是最优路径。
模型中以出行时间为优化目标函数,将路段的拥挤程度分级,并对路段通行能力,即车流大小进行赋权。把动态交通网络图规范成为一个平面图,研究时取东南西北四个方位,模型每一路段用坐标表示。模型将出行者要到达目的地所经过的路段分为三种,由信息搜集系统读取当前路段的位置(Cx,Cy)与当前路段类型值N,根据路段类型值判断该路段类型:当N=0时,当前路段为较为拥挤路段;当N=1时,当前路段为正常通行路段;当N=2时,当前路段为交通事故路段或施工禁行路段。一般用户出行优先级P=0,为低优先级分组;军用以及其他一些高优先级用户P=1。
(三)算法实现步骤
1.蜂群智能算法
蜂群算法是一种新型的元启发式仿生算法。它是模仿蜜蜂行为提出的一种优化方法,是集群智能思想的一个具体应用,它的主要特点是不需要了解问题的特殊信息,只需要对问题进行优劣的比较,通过各人工蜂个体的局部寻优行为,最终在群体中使全局最优值突现出来,有着较快的收敛速度。将蜂群算法做一改进,运用到本模型中,提高了全局搜索能力,具有较快的收敛速度。
2.蜂群算法实现步骤
(1)读取当前路段的坐标(Cx,Cy)与当前路段类型值N;
(2)读取用户目的路段坐标(Dx,Dy)与该用户的优先级值P;根据该优先级值判断分组优先级:当P=0时,分组为低优先级分组,当P=1时,分组为高优先级分组;
(3)根据当前路段坐标(Cx,Cy)、目的路段坐标(Dx,Dy)、当前路段类型和分组优先级确定最短路径输出端口集合:O={o|o⊂(东,南,西,北,本地)}:
a.如果 Cx=Dx且 Cy=Dy,则 O={本地},执行步骤(5),否则执行步骤b;
b.如果 N=0,当时 P=0,执行步骤 c;当 P=1 时,执行步骤d;
c.如果N=2,为了模型普遍适用性,这里假设禁行路段附近不能通行的所有路段为一个禁行路段群。选取禁行路段群东北角路段坐标(Rx,Ry)和西南角路段坐标(R′x,R′y);根据当前路段坐标(Cx,Cy)、目的路段坐标(Dx,Dy)、禁行或者拥挤路段的东北角路段坐标(Rx,Ry)和西南角路段坐标(R′x,R′y)确定最短绕道路径的输出端口:
(a) 当 Cx=Rx,R′x〈Cy〈Ry且 Dx≤R′x,R′y〈Dy〈Ry时,或者当 Cx=R′x,R′y〈Cy〈Ry且 Dx≥Rx,R′y〈Dy〈Ry时,如果 Cy+Dy-Ry-R′x≥0,则 O={北},否则 O={南};
(b).当 Cy=R′y,R′x〈Cy〈Ry且 Dy≤R′y,R′x〈Dx〈Rx时,或者当 Cy=Ry,R′x〈Dx〈Rx且 Dy≤R′y,R′x〈Dx〈Rx是,如果 Cx+Dx-Rx-R′x≥0,则 O={东},否则 O={西};
满足上述(a)或(b)时,执行步骤(5);其它情况下执行步骤d;
d.如果 N=1,根据当前路段坐标(Cx,Cy)和目的路段坐标(Dx,Dy)确定最短路径输出口集合O={o|o⊂(东,南,西,北,本地)}:
(a)当 Cx=Dx且 Cy〉Dy时,O={南},当 Cx=Dx且 Cy〈Dy时,O={北},当 Cy=Dy且 Cx〉Dx时,O={西},当 Cy=Dy且 Cx〈Dx时,O={东};执行步骤(5);
(b)当 Cx〉Dx且 Cy〈Dy时,O={西,南},当 Cx〉Dx且Cy〉Dy时,O={西,北},当 Cx〈Dx且 Cy〈Dy时,O={西,南},当 Cx〉Dx且 Cy〉Dy时,O={东,北};执行步骤(4),从当前路段读取输出端口对应下一路段的状态参数并计算输出端口的选择代价:
(4)a.根据当前路段坐标(Cx,Cy)和输出端口判断输出端口对应的下一路段坐标(Nx,Ny):当输出端口为东时,(Nx,Ny)=(Cx+1,Cy),输出端口为西时,(Nx,Ny)=(Cx-1,Cy),当输出端口为南时,当 (Nx,Ny)=(Cx1,Cy-1)输出端口为北时,(Nx,Ny)=(Cx,Cy+1);
b.根据输出端口对应的下一路段坐标(Nx,Ny)、禁行路段的东北角路段坐标(Rx,Ry)和西南角路段坐标(R′x,R′y),判断下一路段是否属于禁行路段:当R′x〈Nx〈Rx且 R′y〈Ny〈Ry,下一路段为禁行路段,令w3=9999,否则,令 w3=1;
(5)确定输出端口:如果最短路径输出端口集合中仅存在一个输出端口,选择该端口作为输出端口;如果最短路径输出端口集合中存在两个输出端口,选择输出端口选择代价小的作为输出端口。
二、计算机仿真研究
城市汽车导航系统路径选择分配优化程序采用C语言程序运行通过。为验证模型的实用价值,选择赣州市章贡区作为仿真研究的对象,赣州市章贡区的交通地图,如图1所示。
模型假设出行者从图1右上角赣南医学院出发,目的地是左下角的赣州黄金机场。地图优化函数为出行者从出发点到达目的地所需花费的总时间,要求出行者根据当前的实时交通状况,选择一条最短时间到达的路线。
实际交通图路况复杂,且不便于量化研究。为了方便研究,将交通图进行简化,省去车辆不可能行驶的路段,将车辆首先选取章贡区某个交通流量时段的交通进行研究,对该时段各条路段上的交通流大小进行赋权,仿真得到最短时间的路线比较图见图2。实线箭头代表的是最短路径到达,虚线是仿真程序得到的最优路径,通过对比到达时间可以发现,仿真得到的路线优于最短路径。
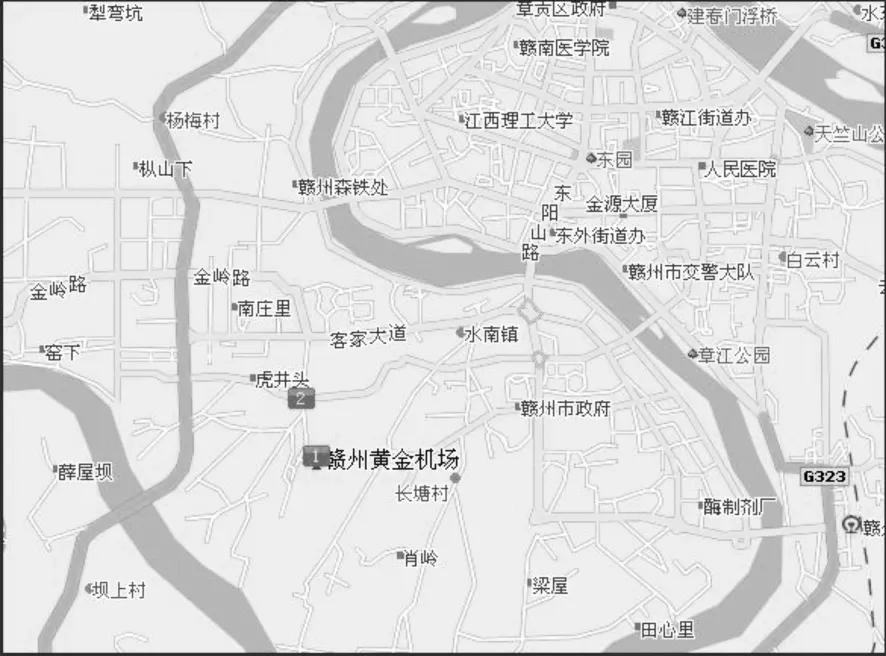
图1 赣州市章贡区交通地图
在编各路段的长度根据地图比例尺计算得出如表1。
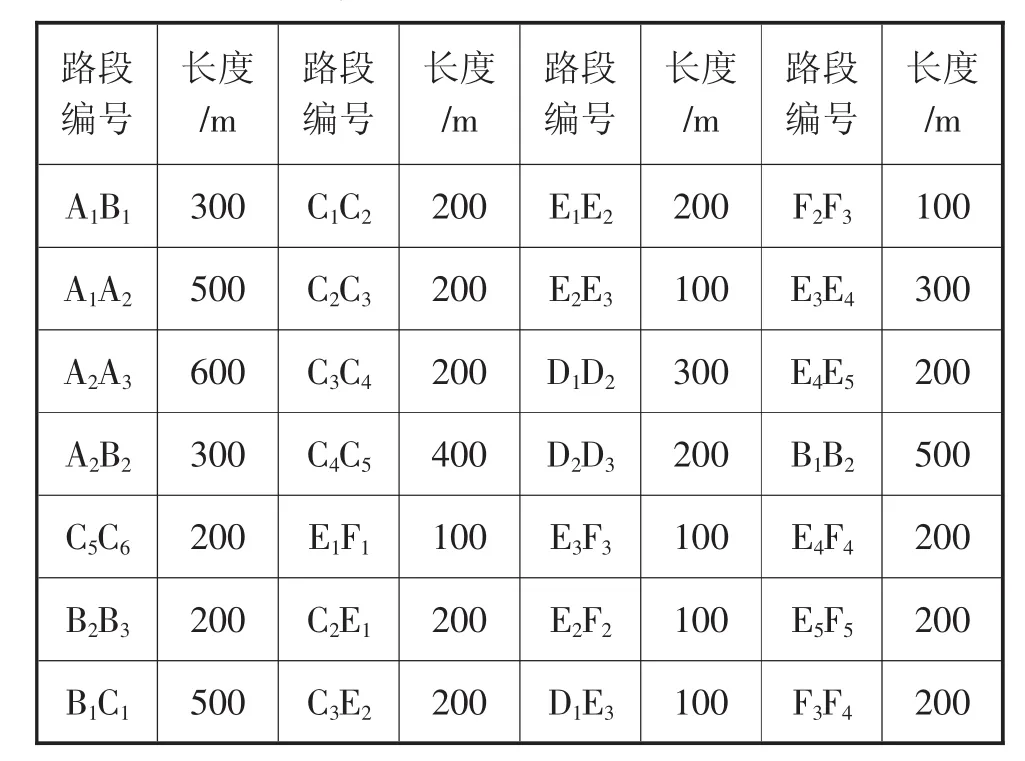
表1 在编路段长度
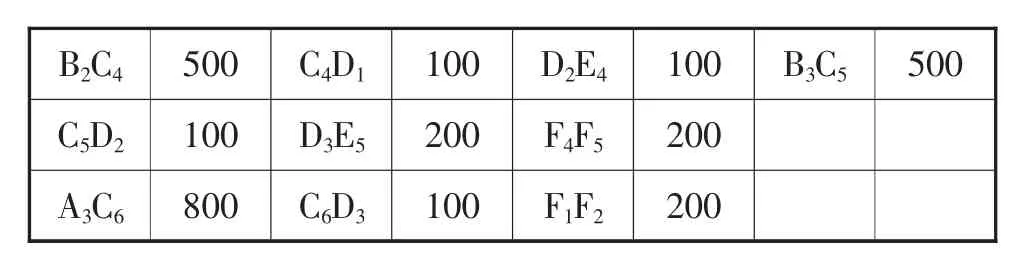
B2C4 500 C4D1 100 D2E4 100 B3C5 500 C5D2 100 D3E5 200 F4F5 200 A3C6 800 C6D3 100 F1F2 200
单一实例不具有说服力,对一天当中16个不同车流量时段各条道路上的车流分别赋权,仿真程序在静态网络的最短距离下和动态网络的路径最优两种情况下,得出结果如图3所示。
图3横坐标为起讫点间所选路段集合的一个交通流权值平均,纵坐标为通过总时间,单位为分钟。利用Excel软件,菱形线表示静态交通网络下的最短路径通过时间,随着交通流的增大时间也相应增大;方形线表示动态交通流下最优路径通过时间,随着交通流的增大时间也相应增大。X-交通流,Y-最短路径。
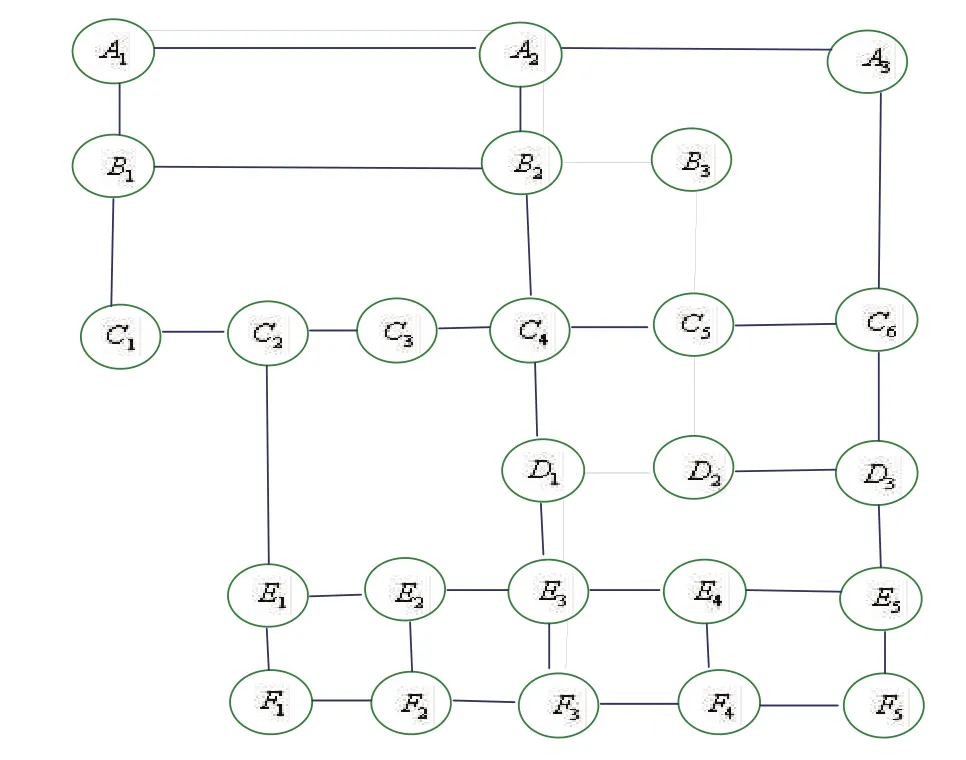
图2 赣州市章贡区交通简化图

图3 动态优化路径选择情况
通过仿真可以发现,在相同交通流权值平均下,选择最小交通流下最优路径所需的通过时间要小于选择静态交通网络下最短路径所需的通过时间。实验结果表明:对于城市交通而言,最优路径并不是距离最短路径,而应该是最不拥挤的路径,本质上是时间最省路径。本文的优化模型与算法是在每下一路段前通过双向信息传输技术得到的车流信息进行一次比较计算,具有实际应用价值。对本文的仿真来说,车辆的行驶速度与实际是一样的,并且简化的赣州市章贡区交通图也与实际基本相符,对于更大规模的交通网络同样适用。利用本算法,对城市交通网络的路径优化是有效的。
三、结论
在动态城市交通网络里,静态网络下的最短路径并不一定是最优路径,在拥挤的城市交通网络中,出行车辆从距离最短路径的起点到终点花费的时间往往要大于交通顺畅的距离较长路径。同时,也说明交通网络里,节点之间静态距离越短,车流量越大,就越容易造成车流堵塞,不利于车辆快速通行。
[1]杨兆升,姜桂艳.城市交通流诱导系统结构框架研究[J].公路交通科技,2007,(4):15-17.
[2]许伦辉.基于最短路径算法的用户最优动态配流模型[J].暨南大学学报,2008,(19):23-26.
