强跟踪UKFNN的泥石流泥位突变状态动态演化
2018-03-08苏盈盈康东帅刘兴华李太福王兴龙
苏盈盈,康东帅,刘兴华,李太福,王兴龙
(1.重庆科技学院 电气与信息工程学院,重庆 401331; 2.新疆克拉玛依天泰机动车尾气检测中心,新疆 克拉玛依 834000)
0 引言
泥石流是山区常见的自然灾害,它介于水流与滑坡之间,是固体物质含量高的固液两相混合流变体,可分为暴雨型、冰川型、冻融型[1];具有暴发突然、来势凶猛、历时短暂、破坏力极强的特点,严重影响山区经济、社会可持续发展[2]。
泥石流的形成机理十分复杂,涉及因素众多,现行的泥石流预报方法分为:监测降雨量预报法、传感器预报法、超声波泥位预报法、遥测地声预报[3-5]。监测降雨量预报法是对于某条沟或相邻几条沟的小规模地区范围泥石流的临近预报;传感器预报法是通过量测传感器被淹没的多少来确定和发报泥石流是否发生及其发生的规模;超声波泥位预报法是利用回声测距的原理,测得传感器断面的泥石流流深;遥测地声预报是利用泥石流地声的声音频率进行预报[6-8]。NelCaine于1980年首次提出了浅层滑坡和泥石流的降雨强度一历时阈值[9];之后,棚桥由彦等提出了泥石流灾害暴发时1h雨强与当日降雨量组合判别式[10];Francesco Fiorillo等建立了泥石流启动的降雨强度一历时临界值;Cannon S.H.等建立了不同地区泥石流的降雨强度—历时关系式[11-12]。
但由于泥石流发生背景的复杂性以及对其形成机理和汇流规律的认识不深,很多相关的预测算法在时变性方面精确度较低,实时跟踪预报的准确度有待提高[13]。混沌学认为任何非线性系统的推演规律都隐藏在其单变量时间序列之中[14],因此,可以通过传感器远程获取泥位的实时数据,选择最佳维数和延迟时间,进行相空间重构,再根据UKF(unscented kalman filter)算法收敛速度快,对噪声适应能力强,处理非线性模型精度高等特点[15];将UKF与BP神经网络进行有效的融合,建立一种适应于泥位突变状态的动态演化方法,可为泥石流的发生提供预警参考。
1 UKFNN理论方法
1.1 无迹卡尔曼的基本原理
UKF算法适用于任意非线性模型,对突变信号具有较强适应能力。它通过概率统计近似的方法来计算方差和均值,可以有效提高预测模型的精度与稳定性。算法步骤如下:


(1)
可得公式:
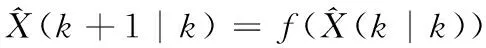
(2)
O+V(k)
(3)
那么从k时刻到k+1时刻X(k+1)的预测值为:
(4)
可得式:
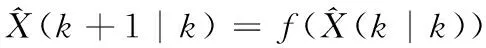
(5)
1)则可以利用式(1)计算X(k)的采样点(ξi(k|k)和其对应的权值Wi。
2)根据状态方程(5),可以得到(ξi(k|k)采样点的一步预测:
(ξi(k+1|k)=f((ξi(k|k))
(6)
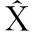
(7)
这里ξi(k|k)为X(k)的2nx+1个Sigma采样点,根据yi=g(xi),i=0,…2nx的UT(unscented transform)变化之后的变量均值与采样点ξi(k|k)的关系可得:
(8)
(9)

P(k+1|k)=E{[f(k,X(k))-(k+1|k][f(k,X(k))-
(10)
根据样本协方差P=Px的UT变化之后的变量协方差公式与原始采样点ξi(k|k)的关系可得:
(11)

ξi(k+1|k)=h(ξi(k+1|k))
(12)
4)则预测量测相应的协方差为:
(13)
其中:ξi(k+1|k)=h(k+1,ξi(k+1|k))。
同理根据UT变化之后的变量协方差公式与原始采样点ξi(k+1|k)的关系可得:
(14)
其中:
(15)
这里,Pzz是测量方差矩阵;Pxz是状态向量与测量值的协方差矩阵。
5)计算UKF增益,更新状态向量和方差
(16)
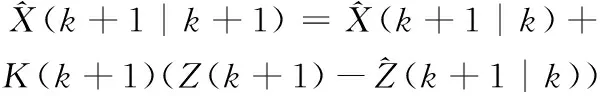
(17)
P(k+1|k+1)=P(k+1|k)-K(k+1)PzzK(k+1)T
(18)
1.2 基于无迹Kalman的神经网络
UKF是将神经网络的权值、阀值作为UKF的状态变量,神经网络的输出作为UKF的测量变量。这样就把问题转化为状态参数的估计问题,然后对系统泥位数据进行动态估计,使得到的空间系统逼近模型更加准确反映出系统的动态时变特性。
相应的过程为:
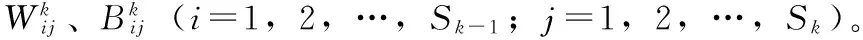
(19)
若Yek为期望输出,则系统的状态和观测方程:
(20)
其中:FN为神经网络第N层传递函数,Xk为输入矢量,Yrk为实际输出。Vk为观测噪声,它是随机白噪声,在UKF神经网络中设为零。
2 基于UKFNN的泥位动态演化模型的建立
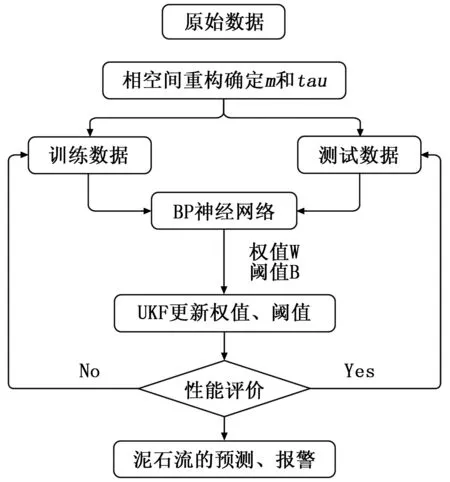
图1 动态演化模型的建立
动态演化模型的建立流程,如图1所示。将整理好的泥位时间序列提取出来,再通过相空间重构确定的两个重要参数m和tau,重新构建泥位样本空间,用BP神经网络算法训练数据,得到神经网络的最优权值、阈值,再将这些权值、阈值构成状态向量,利用UKF对跟新后的样本数据进行递推估计,得到动态的权值、阈值,建立动态演化的UKFNN泥位模型,最后进行泥位的预测和泥石流灾害的预警。
2.1 历史数据的相空间重构
针对我国川藏地区林芝市泥石流自然灾害问题,运用传感器检测得到有关泥石流泥位的数据,从2013-01-01到2013-07-27,一共208天的原始泥位数据如表1所示。这些泥位数据具有单变量混沌时间序列特征。因此,在构建动态模型之前,需要对泥位单变量混沌时间序列进行相空间重构。它的基本思想是:系统中任一分量的演化都是由与之相互作用着的其它分量所决定的,为了重构一个等价的状态空间,只需考察一个分量,并将它在某些固定的时间延迟点上的测量作为新维处理,便确定了某个多维状态空间中的一点。

表1 泥位数据信息
相空间重构技术有两个关键参数:即嵌入维m和时间延迟tau的确定。在Takens定理中,对于理想的无限长和无噪声的一维时间序列,嵌入维m和时间延迟t可以取任意值,但在实际应用中大都是含有噪声的有限长序列(泥位数据也属于此类),嵌入维数和时间延迟是不能任意取值,否则会严重影响重构的相空间质量。
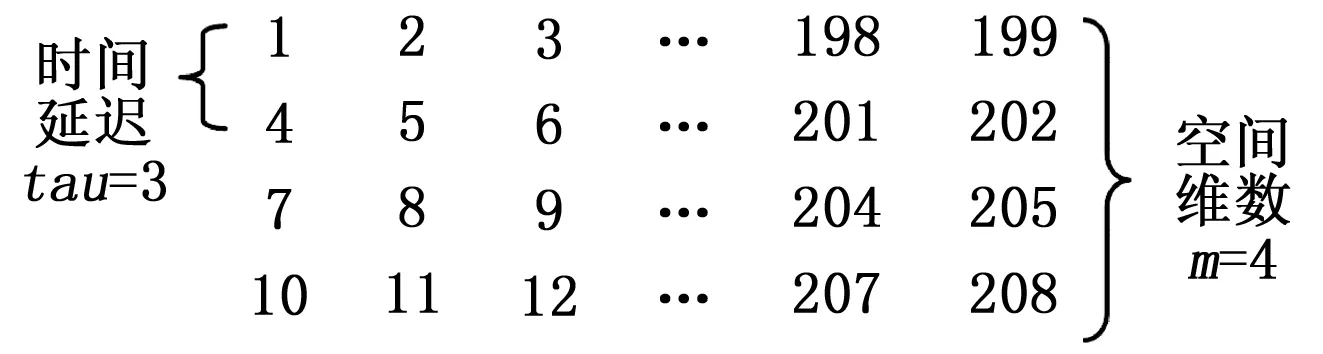
图2 嵌入维数和延迟时间原理
经过实验可得,本文泥位数据的嵌入空间维数m为4;时间延迟tau为3。作为相空间重构法的核心,如图2所示,可将从2013-01-01到2013-07-27,一共208天的原始一维泥位数据,处理成多维数据,即以3个时间周期为延迟的4维泥位变量,可以有效提取出原始数据的动态时变特性,作为BP神经网络输入层的输入变量。
2.2 神经网络隐层节点数选择
均方误差(MSE,meansquarederror)是衡量平均误差的一种较方便的方法,可对模型的精度进行有效评价,这里利用MSE对BP神经网络的隐层节点进行选择,公式如下:
(21)
为了调试出最佳的隐层节点数n,得到最小的均方误差值MSE,将n从6依次试验到12,经过反复测试,依次得到不同结构下UKFNN的平均均方误差,见表2。

表2 隐层节点数n和相应的均方误差MSE值
可以看出,最佳建模网络结构为4-9-1,从单变量泥位数据重构为4维输入变量(以3个时间周期为延迟)、隐含层9个节点、输出为下一周期的泥位值。
2.3 UKFNN泥位的训练模型
通过在川藏林芝冰川区布控的传感器获得实际的泥位观测数据,包括古乡沟、松宗沟、九松沟、嘎朗沟、培龙沟、检它弄巴,共6个测控区域。利用BPNN对其进行建模,获得最佳BPNN模型精度,再利用UKF进行递推计算,不断的在线学习训练。将神经网络的权值、阈值作为UKF的状态变量,神经网络的输出作为UKF的测量变量,并对测量变量进行不断地递推演化,建立精度更高地泥石流预报模型。
以古乡沟为例,将UKFNN与BPNN两种模型下的网络输出进行对比,如图3所示,可看出UKFNN在泥位突变状态下的动态跟踪效果更好,从2013-02-20到2013-04-10的50天泥位突变实验数据来看,UKFNN算法能较好地适应泥位信号的突变,不会出现较大波动。将古乡沟区在两种模型下的网络输出误差及其百分比进行对比,如图4所示,UKFNN动态演化模型的误差百分比多稳定于0.2%以下,而BPNN模型误差百分比多处超过0.5%,表明UKFNN的动态演化模型更能够适应对象的突变状态,输出结果更加稳定。

图3 古乡沟区在两种模型下真实值与训练值的对比
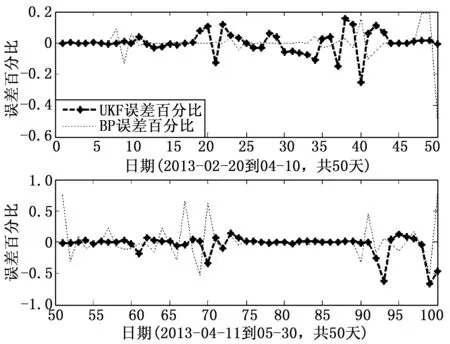
图4 古乡沟区两种模型下的误差百分比的对比
实验结果表明:UKF算法通过确定性采样得到的一组样本点,从而可获得更多的观测假设,对系统状态的均值和协方差的估计更为准确,UKF滤波方法算法对神经网络权值、阈值的递推估计更为准确,建立的模型预测精度更高。
3 动态演化模型的检验与应用
利用UKFNN方法建立林芝市6个地区的泥位演化模型后,可对6个地区的泥位未来一天的泥位预测,并进行图视化预警,以指导实际的安全生产和人民生活,并可作为气象和环境相关部门进行泥石流相关工作的基本参考,提前做出相应的预防措施。
3.1 林芝市6个地区2013年7月27日的泥位预测
利用2013年1月1日~7月25日的泥位的监测值数据,在建立了UKFNN泥位动态演化模型的基础上,对比BP神经网络模型,获得7月27日林芝市6个地区的泥位预测数据,如表3所示。

表3 2013-7-27林芝市6个地区泥位预测数据
从整体来看,BP模型的预测误差百分比在±1.0%之间,而UKF模型的预测误差百分比在±0.5%之间;表明UKFNN可以有效地跟踪泥位信息,建立的动态演化模型也更加精确,对泥石流的泥位具有良好的预测能力。
3.2 林芝市6个地区2013年7月27日泥位预警
林芝市6个地区在UKFNN模型下2013-7-27的泥位真实值、预测值、输出误差及其百分比,见表4。相比BPNN,UKFNN预测模型的预测值与真实值更加贴合,精度较高。按林芝市6个地区泥位值的大小进行分级预警,如图5所示,共分为六个等级。图中可以看出,嘎朗沟、九松沟、古乡沟处于三级预警,较为危险,而松宗沟、培龙沟、检它弄巴处于一、二级预警,较为安全。经过与实际情况对比,上述结论与林芝市实际的泥位情况相符,可为泥石流的发生提供预警作用。

表4 2013-07-27 6个地区泥位等级
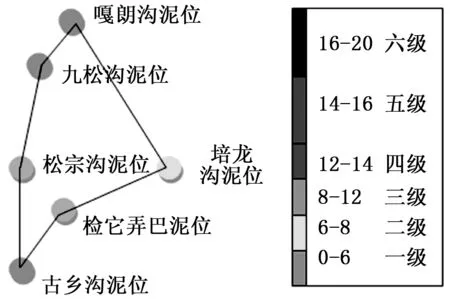
图5 2013-7-27 6个地区泥位预警
4 结论
1)泥位数据具有单变量混沌时间序列特征,而相空间重构法可将原系统的动态信息最大程度地保存下来,通过确定合理的嵌入空间维数和延迟时间,重构出一个等价状态空间,使得数据包含非线性的过程信息,所构建的样本数据能完整表达泥位的演化规律。
2)UKFNN模型将神经网络权值、阀值作为无迹卡尔曼的状态变量,可有效避免权值局部最小化问题,同时构建了一种新的动态神经网络,这种递推演化动态模型可实现泥位的强跟踪预报,降低模型的预测误差。
3)随着时间的延长,该方法能够更好地跟踪泥位数据的变化,不断的进行更新预测,使得模型对非线性时变的泥位数据具有更强的适应能力,从而提高了泥石流的灾前预报精度并分级预警,有着广泛的应用前景。
[1] 师 哲,张平仓,舒安平.泥石流监测预报预警系统研究[J].长江科学院院报,2010,27(11):115-119.
[2] 倪化勇,王德伟.基于雨量(强)条件的泥石流预测预报研究现状、问题与建议[J].灾害学, 2010,25(1):124-128.
[3] 余 斌.根据泥石流沉积物计算泥石流容重的方法研究[J].沉积学报,2008,26(5):789-796.
[4] 徐继维, 张茂省. 泥石流风险评估综述[J].灾害学, 2016, 31(4):157-161.
[5] 崔 鹏, 唐金波, 林鹏智. 泥石流运动阻力特性及其研究进展[J].四川大学学报(工程科学版), 2016, 48(3):1-11.
[6]XianBZ,LiuJP,DongYL,etal.ClassificationandFaciesSequenceModelofSubaqueousDebrisFlows[J]. 《地质学报》英文版,2017,91(2):751-752.
[7]HeSM,OuyangCJ,LiuW,etal.Coupledmodeloftwo-phasedebrisflow,Sedimenttransportandmorphologicalevolution[J].《地质学报》英文版,2016,90(6): 2206-2215.
[8] 潘 泉,杨 峰,叶 亮,等.一类非线性滤波器——UKF综述控制与决策[J].2005,20(5):481-489,494.
[9] 张 喆. 基于BP神经网络的泥石流预测方法研究[D]. 西北民族大学, 2012.
[10] 秦永元.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,2012.
[11] 张洪江,郑国强,程金花,等.不同面积小流域山洪泥石流预报模型研究——以北京市密云县为例[J].灾害学,2011,26(1):65-69,86.
[12] 纪浩哲, 侯丽莹. 山体泥石流危险动态检测方法的应用与实现[J]. 计算机测量与控制, 2013, 21(4):871-873.
[13] 台 伟,范北林,刘士和.长江上游滑坡泥石流预测预警系统[J].武汉大学学报(工学版),2013, 46(6):711-715.
[14] 王永强,张继春.基于相似试验的尾矿库溃坝泥石流预测分析[J].中国安全科学学报,2012, 22(12):70-75.
[15] 黄元江.基于IBRF神经网络的泥石流预测研究[J].中南林业科技大学学报(自然科学版),2010,30(3): 159-163.
