基于视频检测的轨道交通短时客流预测研究

尹 嵘 张炳森 张 宁 徐 文

（1.北京全路通信信号研究设计院集团有限公司，北京 100070；2.北京市高速铁路运行控制系统工程技术研究中心，北京 100070；3.东南大学智能运输系统研究中心轨道交通研究所，南京 210096；4.北京城建设计发展集团股份有限公司，北京 100037）

1 概述

城市轨道交通作为城市公共交通系统中的重要组成部分,已成为缓解道路交通拥堵的重要手段，随着轨道交通的网络化发展以及广大乘客对轨道交通认可度的提高，势必会引起客流时空分布发生巨大的变化，对运营管理提出更高的要求。短时客流预测作为运营管理和资源管理的基础，不仅是运能分析和运量匹配的数据支撑，也是服务水平、系统运行状态评价的重要决策指标[1]，对其进行深入研究具有重要意义。

目前，轨道交通客流短时预测研究刚刚起步，主要集中研究算法的适用性[2]。Feng[3]等人构建随机系数模型对车站的突发客流进行预测，并用分层贝叶斯方法对模型反复评估和更新来提高预测的精度；任崇岭[4]采用小波神经网络对轨道单线路15 min粒度的短时客流量进行预测；刘岩[5]等人在分析线网断面之间相关性的基础上，利用卡尔曼滤波方法对相关断面进行短时客流预测；潘罗敏[6]将时间序列分析预测应用到客流短时预测中。

已有相关研究大多局限于单条线路的短时客流预测，基于站点的短时客流预测研究相对较少，并且现有的预测方法大多以单参数预测为主，如典型的单变量时间序列模型等，鲜有基于多变量的轨道交通客流状态预测，而客流参数之间的关系对于提高预测精度具有重要影响。为此，本文基于视频检测器采集视频统计通道内进站客流的流量和速度参数，在分析两参数之间内在相关性的基础上，构建向量误差修正模型，实现城市轨道交通客流状态的短时预测。

2 基于视频检测的客流参数的获取

近年来计算机对图像处理的能力大幅度提升，能够对视频信息进行实时处理，本文采取较为成熟的方向梯度直方图（Histogram of Oriented Gradient，HOG）特征描述器，结合支持向量机（Support Vector Machine，SVM）分类器识别地铁监控视频中的行人目标[7]，并采用Camshift算法对目标窗口进行跟踪，实现客流参数的统计。检测流程如图1所示。

图1 客流参数检测的流程图

2.1 客流人数统计与速度估算

客流统计过程借助位移矢量判断行人的移动方向，当跟踪目标离开检测区域后，将检测到的最终坐标与发现目标的起始坐标相减，得到跟踪目标的位移矢量。通过与预先定义的进站方向，即正方向进行比对，若两者夹角小于90o，则认为该目标为进站乘客。

由于地铁通道监控摄像头的监控区域是固定的，通过迭代算法的迭代次数可以初步确定目标通过监控区域的时长，结合监控区域的实际长度，可初步估算单个目标通过监控区域的速度。

2.2 训练及数据采集

训练样本选取经典的MIT行人图像库以及INRIA自制行人图像库，用5 000张行人图像作为训练数据集的正样本，任意5 000张非行人目标的图像作为负样本，图像规格统一为64×128，计算得到所有样本的HOG特征，将正样本标记为1，负样本标记为-1，将得到的特征和标签输入SVM中进行训练。

图2和图3是训练中用到的其中一个正样本、一个负样本以及从图像提取出的HOG特征可视化结果。HOG特征由3 780个分量组成，图中纵坐标表示归一化后的结果。

图2 正样本与HOG特征示意图

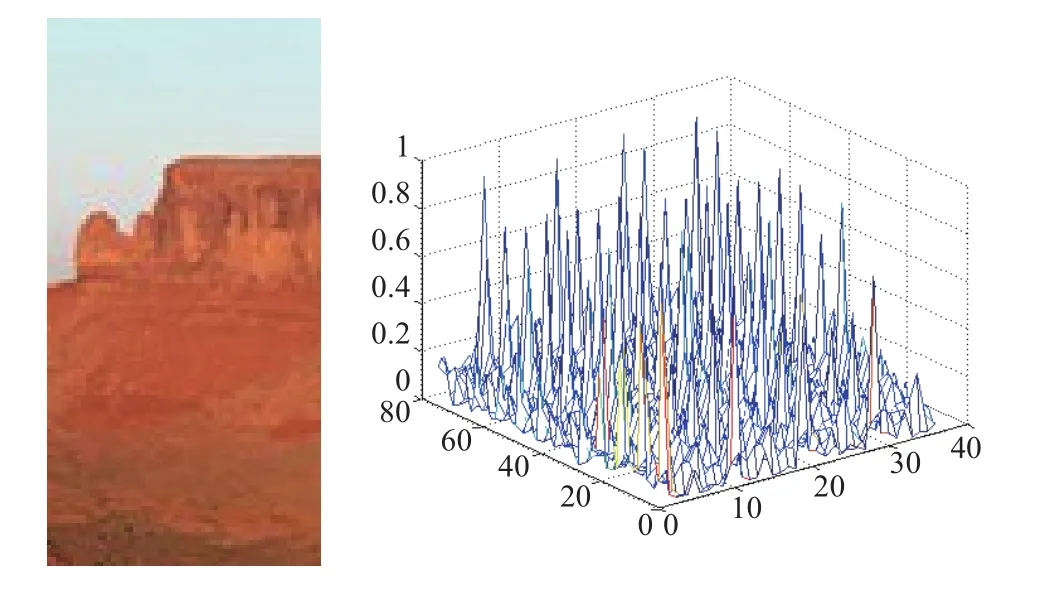
图3 负样本与HOG特征示意图

以提取的工作日早高峰监控视频录像作为实验的测试数据集，5 min为单位统计行人数量，并计算5 min通道内进站客流的平均步行速度。试验中，为提高识别精确度，以5帧为阈值判断目标的合法性，将连续5帧出现的目标加入跟踪队列。若连续5帧跟踪窗口未能检测到匹配的目标，则认为该目标离开监控区，剔除出跟踪序列[8]，并计算其位移矢量。若判断为进站旅客，则客流统计量+1，并计算其通过速度，该方法对参数提取的准确率可达95%。

3 客流预测模型构建

3.1 向量误差修正模型

向量误差修正（Vector error correction，VEC）模型[9]是在向量自回归（Vector Auto-regressive，VAR）模型的基础上，将协整理论[10]与误差修正模型结合起来的一种多变量时间序列建模方法。其基本思想是具有协整关系的变量之间存在长期的均衡关系，而这种关系是通过短期波动不断调整下实现的[11]。首先对客流参数的时间序列单整、多个参数之间协整关系进行检验，如证明客流参数之间存在均衡关系，则存在一种误差修正机制使它们的某些线性组合也是平稳序列，可对该序列构建向量误差修正模型，利用相关变量中的补充信息来提高对个体参数预测的准确性。

向量自回归模型（VAR）表达如下：

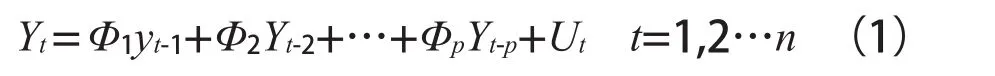
式中：Yt是k维内生变量，且Yt单整；p为滞后阶数；Φ1，Φ2，…Φp是k×k维矩阵；Ut为随机误差项。对式（1）进行差分得：

其中，βʹyt-1=αecmi-1是反映变量长期均衡关系的误差修正项。

则向量时间序列yt在t时刻的预测方程即为：

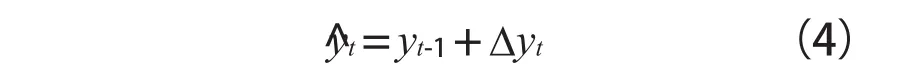
式中，^yt为时间序列yt在t时刻的预测值；yt-1为t-1时刻的实际观测值。

3.2 客流VEC模型构建

由于客流密度参数易受行人间遮挡影响，检测准确性较低，因此采用客流量和速度参数进行多变量预测模型的构建。在协整关系检验和滞后阶数确定的基础上，构建基于客流量和速度的客流状态VEC模型。形式为：

式中，Δqt和Δvt分别为t时刻流量和速度的一阶差分预测值;为误差修正项，α1和α2为修正系数，qt-1和vt-1分别为t-1时刻流量和速度的实际观测值；Δqt-1和Δvt-1是t-1时刻流量和速度的一阶差分值；矩阵aij和bij（i，j=1，2）为短期弹性系数，n为滞后阶数。

t时刻客流和速度的预测方程为：

4 实例分析

使用本文构建的向量误差修正模型,对南京市鼓楼车站4A通道早高峰进站客流状态进行预测。

4.1 数据来源

本文数据来源于2016年8月1-26日一个月内视频检测器采集到的工作日早高峰进站客流画面，用第2节描述的方法采集客流量和速度参数，数据采集时间间隔为5 min。在连续采集的一个月数据中，前3周工作日早高峰的数据作为样本数据，用于模型参数的标定，后一周的数据用于模型预测性能的评估。

4.2 参数标定

4.2.1 客流参数之间协整关系检验

参数之间存在协整关系,才能构建向量误差修正模型，各参数同阶单整是存在协整的前提，采用ADF单位根检验方法对客流量和速度两个参数的原始序列进行平稳性检验，结果表明两者数据时间序列均一阶单整，满足协整对各变量同阶单整的要求。

基于客流量和速度时间序列的一阶单整性，对两个变量进行协整关系检验。采用基于回归系数的Johansen协整检验法，将协整关系检验转化为式（2）压缩矩阵非零特征根个数检验，该方法不仅可以判断出是否存在协整关系，还可以精确检验出协整向量的数目。协整检验结果如表1所示。

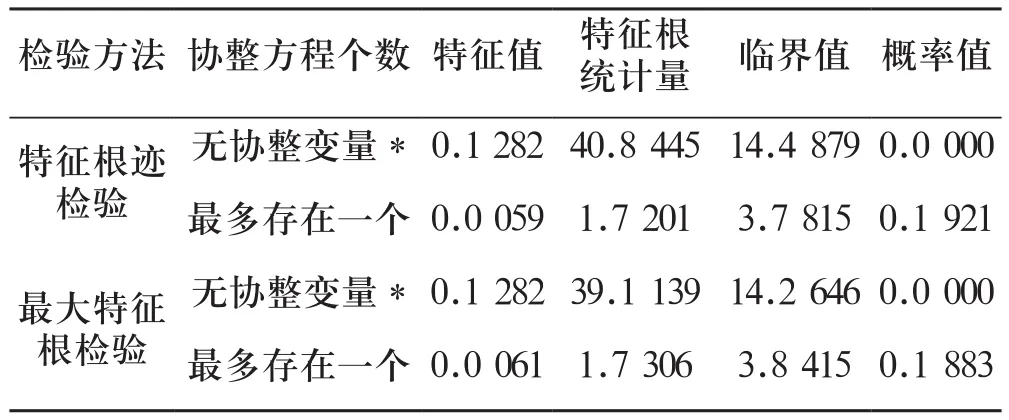
表1 流量和速度Johansen检验结果

结果表明，拒绝了无协整向量的原假设，接受了存在一个协整向量的备选假设，说明客流量和速度之间存在长期的均衡关系，可以构建基于客流和速度的VEC模型。

4.2.2 VEC模型滞后阶数确定

滞后阶数p的选取对模型构建至关重要，既能够完整反映模型的动态特征，也要避免模型自由度的减少。因此综合考虑选取AIC、BIC、SC、HQ四个检验统计量来确定模型构建所需要的滞后阶数。检验结果如表2所示，可以看出VEC模型的最佳滞后阶数是3。

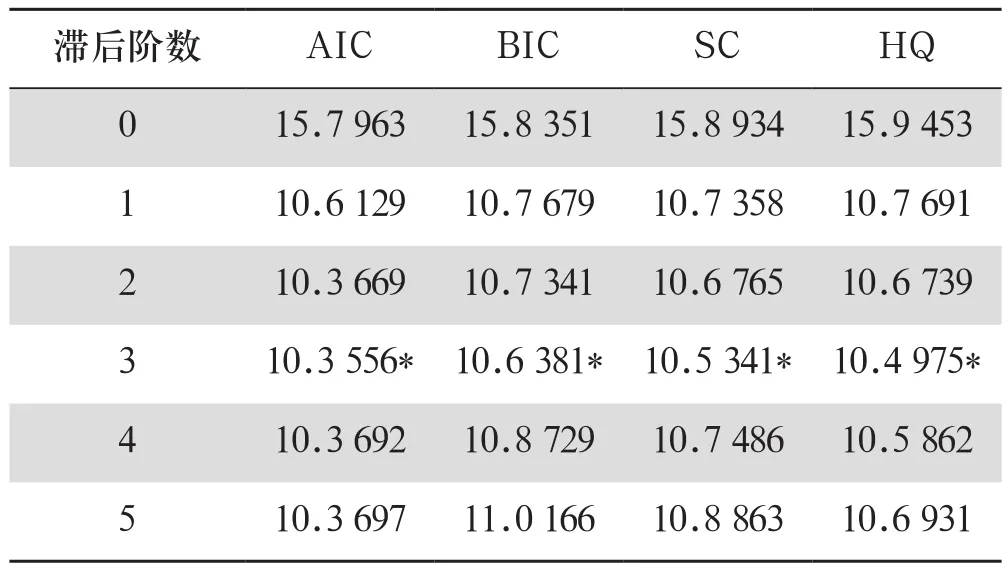
表2 VEC模型滞后阶数的确定

4.2.3 模型稳定性检验

在利用所构建的VEC模型进行预测前，还需对其进行平稳性检验，VEC模型的平稳性检验一般转化为对系数矩阵单位根的检验，当系数矩阵的根在单位圆外时，表明VEC模型满足平稳性条件，该VEC模型的估计及预测结果是有效的。模型稳定性检验结果如图4所示。

可以看出，圆点均落在单位圆内，表明所建立的客流状态多变量预测的VEC模型是平稳有效的。

图4 VEC模型单位根检验

4.2.4 VEC模型参数估计

以8月1日到21日三周工作日早高峰检测的数据为样本数据，用于对模型参数的标定，在显著性水平为α=0.05下，VEC模型参数估计结果如式（7）、（8）：

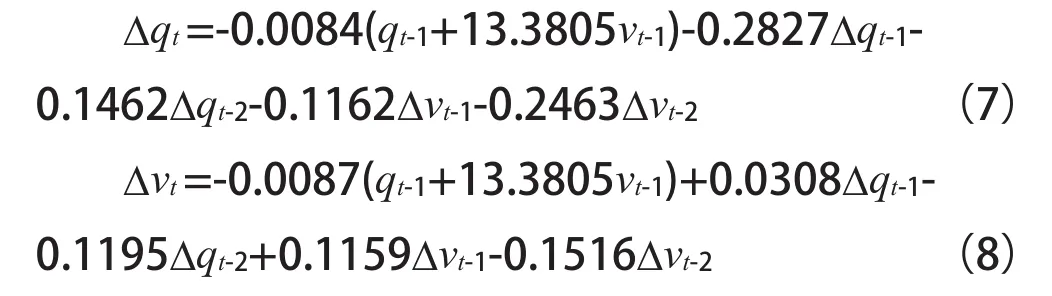
4.3 预测性能评估

4.3.1 评价指标

选取平均绝对误差（MAE）、均方根误差（RMSE）以及平均绝对百分比误差（MAPE）三个指标对VEC模型的性能进行评估。

4.3.2 VEC模型总体预测性能与对比分析

基于上文标定的模型参数，对2016年8月22～26日南京市鼓楼车站4 A通道进站客流进行预测。为了进一步比较多变量时间序列模型与单变量时间序列模型在轨道交通客流预测的性能，采用同样的样本数据构建单变量时间序列模型ARIMA(0,1,1)，并对客流进行预测。

图5和图6分别为23日客流量和速度预测值与实际观测值的拟合效果。

图5 客流量预测效果图

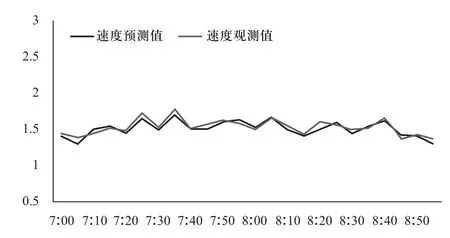
图6 客流速度预测效果图

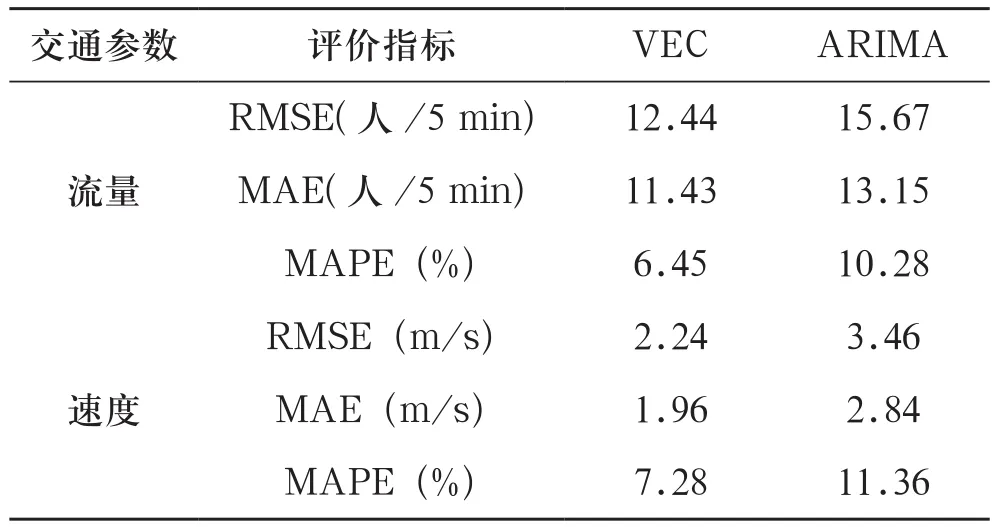
表3 给出VEC模型预测的性能以及与ARIMA模型的对比。

由表3可以看出：1）对于VEC模型来说，两参数预测的准确性都高于90%，客流量预测的准确性高于速度预测的准确性；2）VEC模型在客流量和速度的预测都明显优于ARIMA模型，表明本文所构建的向量误差修正模型具有较好的预测效果。

5 结论

轨道交通客流参数之间存在一定的内在相关性，在客流预测研究中引入经济学领域的向量误差修正模型。在对视频检测器采集到客流进站的画面进行处理统计得到客流和速度参数的前提下，在对两者原始序列进行平稳性检验、协整检验的基础上，构建了客流状态短时预测的多变量时间序列预测模型。实例分析表明，构建的向量误差修正模型具有较好的预测性能，并且明显优于单变量时间序列预测模型，提高了客流短时预测的精度，具有一定的实用价值。

[1]Li J W. Short-Time Passenger Volume Forecasting of Urban Rail Transit Based on Multiple Fusion[J].Applied Mechanics and Materials， 2014，641（9）：773-776.

[2]王雪梅，张宁，张云龙.城市轨道交通短时客流预测体系框架及关键技术[J].交通运输工程与信息学报，2013（2）：107-113.

[3]Feng X,Zhang H,Gan T,et al.Random coefficient modeling research on short-term forecast of passenger flow into an urban rail transit station[J].Transport,2016,31(1):94-99.

[4]任崇岭，曹成铉，李静，等. 基于小波神经网络的短时客流量预测研究[J]. 科学技术与工程，2011，11（21）：5099-5103.

[5]刘岩，张宁，邵星杰.城市轨道交通断面客流短时预测[J]. 都市快轨交通，2015，28（1）：77-81.

[6]潘罗敏. 地铁短时客流量预测预警研究[D]. 北京：首都经济贸易大学，2011.

[7]孙锐，陈军，高隽.基于显著性检测与HOGNMF特征的快速行人检测方法[J].电子与信息学报，2013，35（8）：1921-1926.

[8]徐超，高梦珠，查宇锋.基于HOG和SVM的公交乘客人流量统计算法[J].仪器仪表学报，2015，36（2）：446-452.

[9] Engle R F,Granger C W J.Co-integration and Error Correction:Representation,Estimation,and Testing.[J].Econometrica，1987，55（2）：251-276.

[10]邴其春，杨兆升，周熙阳，等.基于向量误差修正模型的短时交通参数预测[J].吉林大学学报（工），2015，45（4）：1076-1081.