基于Monte Carlo方法的SCV加热s盘管可靠性评价

邓 娇 侯 磊 李丽敏 文亚成

1. 中国石油大学(北京)机械与储运工程学院, 北京 102249;2. 中国市政工程中南设计研究总院, 湖北 武汉 430010;3. 大庆油田采油六厂, 黑龙江 大庆 163114

0 前言

浸没燃烧式气化器(Submerged Combustion Vaporizer,SCV)具有结构紧凑、节省空间、换热效率高、排烟温度低、节省能源等优点,是LNG接收站气化外输系统的重要设备,在冬季作为接收站的气化设备,在其他季节作为备用气化器,其可靠性直接影响气化外输系统的安全运行。SCV的组成复杂,调研结果表明,其他部件均可在调控之后平稳工作,而加热盘管所处的水浴环境pH值为4～6,会发生腐蚀现象,影响SCV的可靠性。目前国内外对于SCV的结构优化设计和操作参数设置进行了研究,未涉及其可靠性评价方面[1]。本文构建SCV可靠性评价模型,建立加热盘管的极限状态方程,计算SCV可靠度,研究加热盘管腐蚀随运行时间和运行压力的变化规律,对站场SCV的运行和维修具有指导意义。

1 SCV结构和工作原理

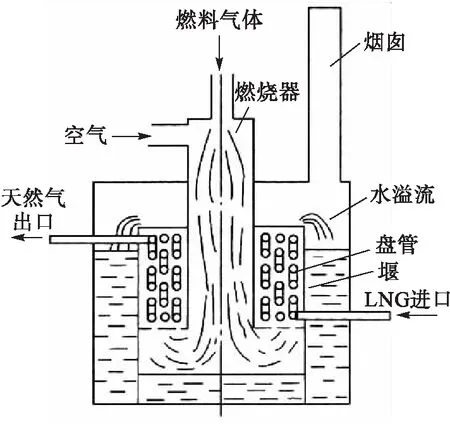
图1 SCV工作原理

2 可靠性评价模型的建立

为评价SCV加热盘管产生腐蚀缺陷时能否在规定的压力下继续运行,利用应力-强度干涉理论和管道腐蚀剩余强度评估标准建立可靠性评价模型。SCV加热盘管的管材是316 L不锈钢,适合于低合金钢剩余强度评价的方法主要有五种[4-11]：美国机械工程师协会颁布的ASME B 31.G-1984适用于管道只有单一的轴向腐蚀缺陷；ASME B 31.G-1991在上一版的基础上进行了改进,对流变应力、鼓胀系数和腐蚀缺陷面积三个影响因素做了修正,计算结果更加精确；ASME B 31.G-2009将评价方法分成四个等级,根据不同的腐蚀情况和收集的数据情况采用不同的评价方法,使得计算结果与实际情况更加符合；美国运输部提出的RSTRENG标准需要非常详细的腐蚀缺陷参数,腐蚀参数主要包括腐蚀区域的形状、长度和宽度；SY/T 6151《钢制管道管体腐蚀损伤评价方法》将管道的腐蚀程度进行层次划分,分类进行评定,这种方法也需要详细且精确的管道腐蚀数据。由于SCV加热盘管只承受内压,现场测得的腐蚀数据为腐蚀长度和腐蚀深度,从载荷类型、最佳适用材料和腐蚀数据的获取情况三方面考虑,采用ASME B 31.G-2009的1级评价方法进行SCV加热盘管腐蚀剩余强度评价。

2.1 建立极限状态方程

ASME B 31.G-2009中要求:当失效压力大于或等于操作压力乘以1个合适的安全系数时,缺陷可以接受[9]。为了评估加热盘管的可靠性,建立加热盘管极限状态函数[12]:

z=pf-ps

(1)

式中:z为加热盘管极限状态函数(z>0,加热盘管可靠;z=0,加热盘管处于极限状态;z<0,加热盘管失效);pf为传热管失效时的压力,MPa;ps为加热盘管的最大安全运行压力,MPa。

(2)

ps=S×p0

(3)

式中:SF为加热盘管发生失效时的环向应力,MPa;D为管道外径,mm;t为管道壁厚,mm;S为安全系数,取S=1.25;p0为加热盘管运行压力,MPa。

加热盘管的失效应力按下面公式计算:

(4)

式中:d为腐蚀深度,mm;M为鼓胀系数;Sflow为流变应力,MPa。

(5)

式中:L为腐蚀长度,mm。

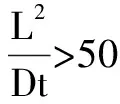
(6)

流变应力表示为：

Sflow=SMYS+69

(7)

式中:SMYS为最小屈服强度,MPa。

对于准稳态腐蚀,腐蚀的长度和深度随时间扩大,T时刻腐蚀长度和腐蚀深度分别为：

L=L0+Va(T-T0)

(8)

d=d0+Vr(T-T0)

(9)

式中:T为现腐蚀检测时间，a；T0为腐蚀检测初始时刻,a;L0为腐蚀检测初始时刻的腐蚀长度,mm;d0为腐蚀检测初始时刻的腐蚀深度,mm;Va为长度腐蚀速率,mm/a;Vr为深度腐蚀速率,mm/a。

将式(2)～(6)带入式(1),可得：

(10)

2.2 Monte Carlo方法仿真过程

Monte Carlo方法通常用于计算有随机变量函数的函数值,通过对独立随机变量进行抽样实验或随机模拟计算,可用于随机函数服从任意分布的函数问题。其收敛速度与随机变量的维数无关,只要所取的循环次数足够多,就可以保证概率计算的准确性和全面性[13-16]。加热盘管的初始腐蚀尺寸、工况载荷、机械强度、轴向及径向腐蚀增长速率等参数具有随机性,本文采取Monte Carlo方法解决加热盘管可靠性评价过程中的随机性问题,定量分析加热盘管的可靠性,仿真步骤如下:

1)确定模型中所有参数的分布规律,对腐蚀缺陷参数和传热管基本参数进行随机抽样,抽样次数N为106。

2)将抽样所得数据代入式(10)中,计算z的值，得到传热管失效压力与最大运行压力的差值Δ p=z。

3)若z≤0,则记为1；若z>0,则记为0；统计失效次数n。

4)计算加热盘管失效概率PF=n/N。

2.3 模型参数的确定

加热盘管腐蚀剩余强度的极限状态方程中包含的参数有管道外径D、管道壁厚t、管道运行压力p0、管道屈服强度SMYS、腐蚀深度d0、腐蚀长度L0、深度腐蚀速率Vr、长度腐蚀速率Va。为简化计算,暂不考虑变量间的相关性,假定各参数相互独立。

这些参数往往不是定值且服从一定的分布规律,通过调研文献可知[17],工况载荷、盘管尺寸和腐蚀区域尺寸的分布规律均可用正态分布描述。选取所有变量为随机变量且均服从正态分布。

3 计算实例

3.1 SCV加热盘管剩余寿命计算

以某LNG接收站SCV加热盘管为例,盘管采用316 L不锈钢[18-20],通过现场调研,加热盘管参数见表1。

表1加热盘管参数

参数均值标准差分布形式外径/mm3175001正态分布壁厚/mm2410001正态分布内压/MPa251正态分布屈服强度/MPa1702正态分布初始腐蚀深度/mm0015正态分布初始腐蚀长度/mm001正态分布深度腐蚀速率/(mm·a-1)0043001正态分布长度腐蚀速率/(mm·a-1)0801正态分布

对表1中的参数进行抽样,计算加热盘管的失效概率。图2为运行10、12、15、18 a的失效概率分布曲线。失效概率随着使用年限的延长而增大,使用年限增长,腐蚀长度和腐蚀深度增加,加热盘管承压面积减少,失效概率增大。图3为加热盘管累积失效概率随时间的变化曲线,累积失效概率随运行时间的增加逐渐增加,运行前期累积失效概率增加缓慢,运行至某一时间,累积失效概率开始迅速增加。加热盘管运行前10 a,累积失效概率较低,可靠度高,运行10 a时的累积失效概率为0.002 99；在运行10～12 a时,累积失效概率开始缓慢上升,可靠度逐渐降低,建议缩短检修周期；从运行12 a开始,累积失效概率开始快速上升,可靠度迅速下降,应密切检查加热盘管的运行情况,及时检修；运行18 a时,其累积失效概率为0.411。

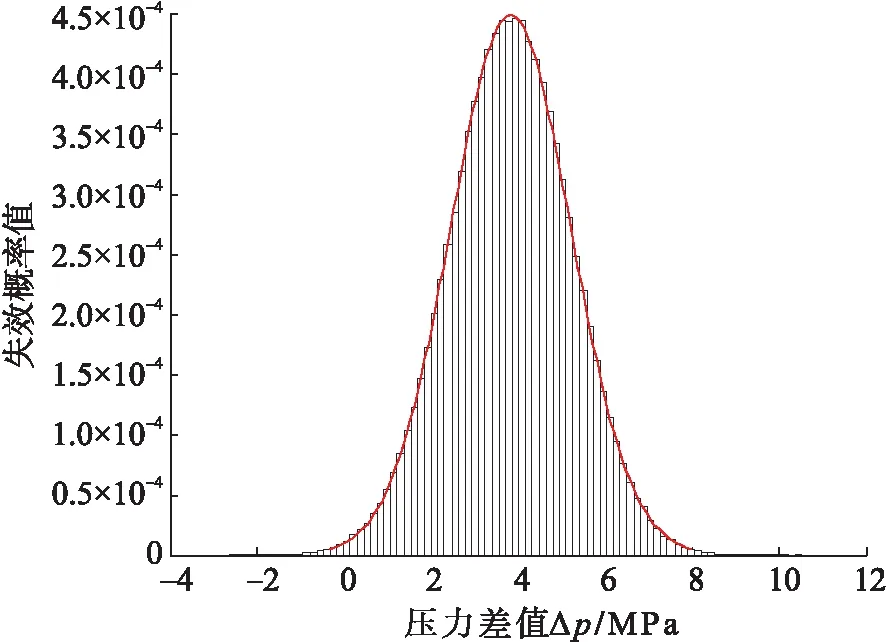
a)投入使用10 a的失效概率曲线

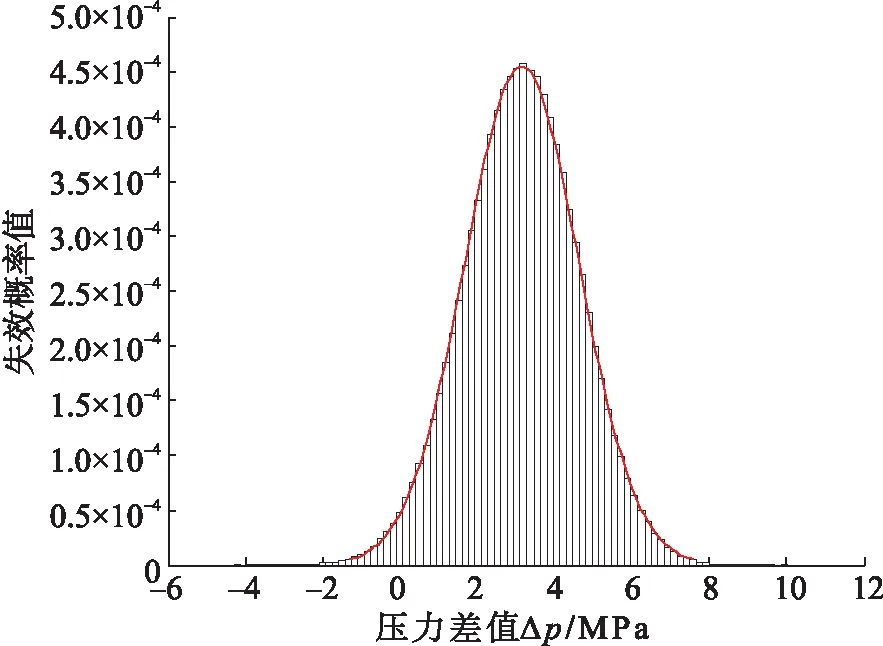
b)投入使用12 a的失效概率曲线

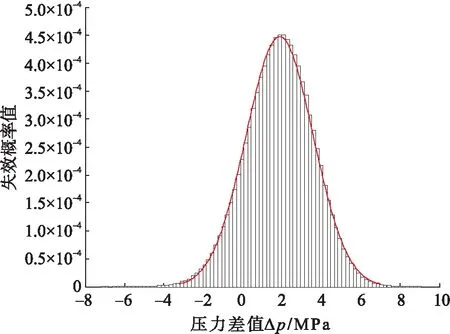
c)投入使用15 a的失效概率曲线

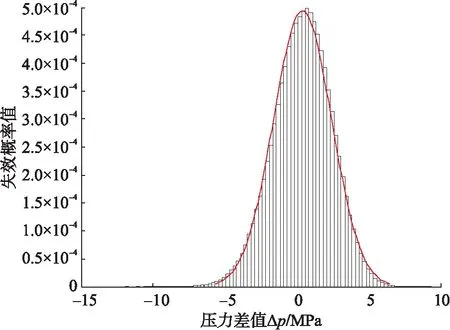
d)投入使用18 a的失效概率曲线图2 加热盘管失效概率分布曲线

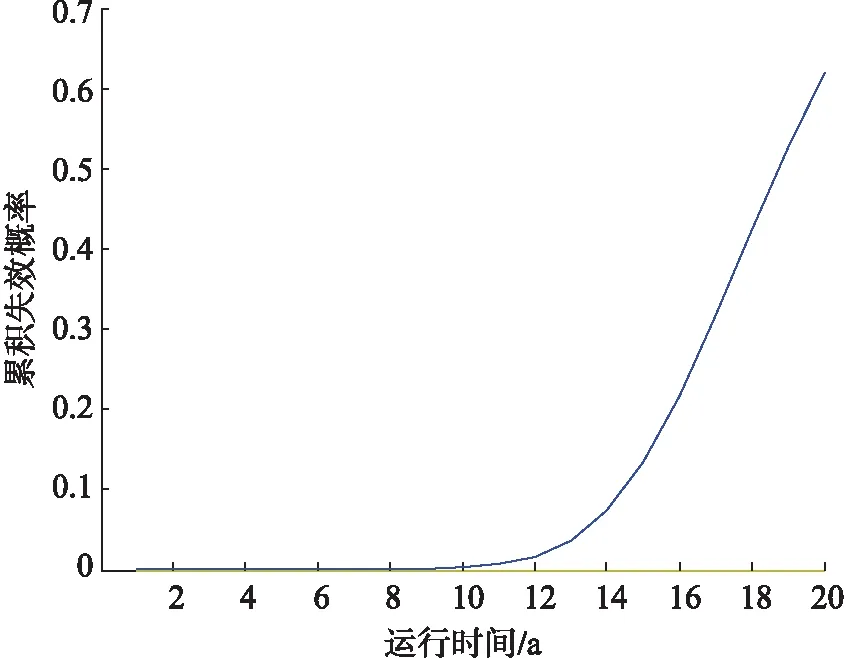
图3 加热盘管累积失效概率随时间的变化曲线

3.2 运行压力对可靠性的影响

在加热盘管的可靠性影响因素中,稳定的腐蚀环境使得腐蚀参数变化较小,而运行压力随着工况的变化而变化,因此主要分析运行压力对加热盘管可靠度的影响。

随着压力的变化,加热盘管失效概率发生变化。以盘管运行10 a为例,选取压力分别为20、23、25 MPa,失效概率分布曲线见图4。随着压力增大,失效概率曲线向坐标横轴负方向移动,失效概率增加。不同运行压力下加热盘管累积失效概率随时间的变化见图5,运行压力为20～22 MPa时,累积失效概率随压力的变化较小,20 a内累积失效概率均较低；运行压力为23～26 MPa时,累积失效概率随压力的增加变化较大,第20 a不同运行压力下累积失效概率均较高。运行20 a,运行压力从22 MPa增加到26 MPa,累积失效概率从0.1上升至0.8。同时,当运行时间较短时,压力的变化对累积失效概率的影响较小,但当运行时间较长时,累积失效概率随压力的变化较大。运行压力从20 MPa增加到26 MPa,运行8 a,累积失效概率均接近0;运行20 a,累积失效概率大约从0上升至0.8。

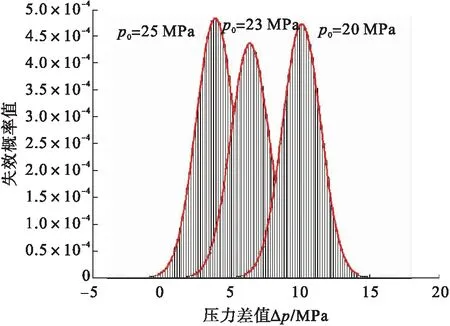
图4 不同运行压力下加热盘管失效概率曲线

图5 不同运行压力下加热盘管累积失效概率随时间的变化曲线

4 结论

1)依据应力-强度干涉理论建立SCV加热盘管的极限状态方程,按照ASME B31.G-2009标准的流程计算加热盘管的失效应力。采用Monte Carlo方法对加热盘管极限状态函数中的参数进行随机抽样,计算加热盘管可靠度和预测加热盘管剩余使用寿命。

2)对某LNG接收站SCV加热盘管进行腐蚀剩余寿命预测,随着使用年限增加,加热盘管失效概率增加,且增加速率逐渐加快。在盘管运行10 a时,其累积失效概率为0.002 99,可靠度为0.997;运行18 a时,其累积失效概率为0.411,可靠度为0.589。若以0.8为可靠度下限,则盘管使用寿命为14 a。

3)随着盘管运行压力的上升,其可靠度下降。当运行年限较短时,运行压力对盘管可靠度影响较小,当运行年限较长时,盘管可靠度随运行压力的增加迅速上升。运行20 a,压力20 ～22 MPa,加热盘管可靠度高于0.9,压力23 ～26 MPa,加热盘管可靠度从0.8下降至0.2。

[1] 于国杰.LNG沉浸式燃烧型气化器数值模拟[D].大连:大连理工大学,2009:21-25.

Yu Guojie. Numerical Simulation of LNG Submerged-Combustion Vaporizer [D]. Dalian: Dalian University of Technology, 2009: 21-25.

[2] 刘世俊,郭 超.浸没燃烧法在LNG气化工艺中的应用[J].城市燃气,2015,12(490):22-27.

Liu Shijun, Guo Chao. Application of Immersion Combustion Method in LNG Gasification Process [J]. Urban Gas, 2015, 12 (490): 22-27.

[3] 程云东.浸没燃烧式气化器的设计缺陷及改进方法[J].油气储运,2014,33(3):292-294.

Cheng Yundong. Design Defects and Modification of Submerged Combustion Vaporizer [J]. Oil & Gas Storage and Transportation,2014, 33 (3): 292-294.

[4] 俞树荣,李建华,李淑欣,等.埋地管道腐蚀剩余寿命预测概率模型[J].中国安全科学学报,2008,18(6):11-15.

Yu Shurong, Li Jianhua, Li Shuxin, et al. Probability Model for the Prediction of Corrosion Remaining Life of Underground Pipelines [J]. China Safety Science Journal, 2008, 18 (6): 11-15.

[5] 帅 健.腐蚀管线的剩余寿命预测[J].中国石油大学学报:自然科学版,2003,27(4):91-93.

Shuai Jian. Prediction Method for Remaining Life of Corroded Pipelines [J]. Journal of the University of Petroleum, China: Edition of Natural Science, 2003, 27 (4): 91-93.

[6] 黄亚晖,周丽丽.B31.G腐蚀管道剩余强度评价比较分析[J].天然气与石油,2012,30(4):62-66.

Huang Yahui, Zhou Lili. Evaluation on Residual Strength of Corroded B31. G Pipelines [J]. Natural Gas and Oil, 2012, 30 (4): 62-66.

[7] 何东升,郭 简,张 鹏.腐蚀管道剩余强度评价方法及其应用[J].石油学报,2007,28(6):125-128.

He Dongsheng, Guo Jian, Zhang Peng. Assessment Method for Remaining Strength of Corroded Pipeline and Its Application [J]. Acta Petrolei Sinica, 2007, 28 (6): 125-128.

[8] Kiefner J F, Vieth P H. A Modified Criterion for Evaluating the Remaining Strength of Corroded Pipe [M]. Columbus: Battelle Memorial Institute, 1989: 63-74.

[9] American Society of Mechanical Engineers. Manual of Det-ermining the Remaining Strength of Corroded Pipelines: ASME B31 G-1984 [S]. New York: ASME, 1984: 4-7.

[10] American Society of Mechanical Engineers. Manual of Det-ermining the Remaining Strength of Corroded Pipelines: ASME B31 G-1991[S]. New York: ASME, 1991: 4-7.

[11] American Society of Mechanical Engineers. Manual for Det-ermining the Remaining Strength of Corroded Pipelines: ASME B31 G-2009[S]. New York: ASME, 2009: 8-15.

[12] Petroleum and Natural Gas Industries. Pipeline Transportation Systems-Reliability-Based Limit State Methods: ISO 16708[S]. Geneva: ISO, 2006: 325-327.

[13] 赵 磊.重要性抽样Monte-Carlo法在概率断裂力学分析中的应用研究[D].杭州:浙江工业大学,2013: 25-27.

Zhao Lei. Research on the Application of the Monto-Carlo Simulation Based on Importance Sampling Method in the Analysis of Probabilistic Fracture Mechanics [D]. Hangzhou: Zhejiang University of Technology, 2013: 25-27.

[14] 张仙风,吕志鹏.基于MATLAB的蒙特卡罗方法在可靠性设计中的应用[J].装备制造技术,2006,(4):82-83.

Zhang Xianfeng, Lv Zhipeng. The Application of MATLAB-based Monte Carlo Method in Reliability Design [J]. Equipment Manufacturing Technology, 2006, (4): 82-83.

[15] 孙春梅,李 琴,黄志强,等.基于Monte Carlo方法的腐蚀管道可靠性分析[J].油气储运,2015,34(8):811-816.

Sun Chunmei, Li Qin, Huang Zhiqiang, et al. Reliability Analysis of Corroded Pipelines Based on Monte Carlo Method [J]. Oil & Gas Storage and Transportation, 2015, 34 (8): 811-816.

[16] 张 崎,李兴斯.结构可靠性分析的模拟重要抽样方法[J].工程力学,2007,24(1):33-36.

Zhang Qi, Li Xingsi. Importance Sampling Approach in Structural Reliability Analysis Based on Kriging Simulation [J]. Engineering Mechanics, 2007, 24 (1): 33-36.

[17] 燕秀发,谢禹钧,戴 耀.压力管道可靠性安全评定[J].机械设计与造,2004,2(1):6-8.

Yan Xiufa, Xie Yujun, Dai Yao. Pressure Pipings Reliability Safety Assessment [J]. Machinery Design and Manufacture, 2004, 2 (1): 6-8.

[18] 曾初升.316 L不锈钢腐蚀性能电化学研究[D].昆明:昆明理工大学,2006:65-85.

Zeng Chusheng. Electrochemical Study on Corrosion Behavior of 316 L Stainless Steel [D]. Kunming: Kunming University of Science and Technology, 2006: 65-85.

[19] 李 阳.316 L不锈钢焊接接头的微观组织及点蚀性能[D].长春:吉林大学,2015:21-28.

Li Yang. The Microstructure and Pitting Corrosion Property of the 316 L Stainless Steel Welded Joint [D]. Changchun: Jilin University, 2015: 21-28.

[20] 张艳丽.X 65碳钢和316 L不锈钢在模拟油田采出水中的腐蚀行为研究[D].青岛:中国海洋大学,2014.

Zhang Yanli. Corrosion Behavior of X 65 Carbon Steel and 316 L Stainless Steel in Simulated Oilfield Product Water [D]. Qingdao: Ocean University of China, 2014.