两水平修理策略的k/n(G)表决系统可靠性分析
2018-03-06吴文青唐应辉张元元
吴文青,唐应辉,张元元
(1.西南科技大学理学院,四川绵阳 621010;2.四川师范大学数学与软件科学学院,四川成都 610066)
1 引 言
k/n(G)表决系统由n个部件组成,当n个部件中至少有k个部件同时正常工作时,系统才正常运转(1≤k≤n),即当故障的部件数等于n-k+1时系统就故障.关于k/n(G)表决系统的基本理论及相关研究成果可见文献[1,2].在k/n(G)表决系统中,若k=1,则系统退化成n部件并联系统,此时系统故障当且仅当n个部件全部处于故障状态.若k=n,则系统退化成n部件串联系统,此时系统故障当且仅当n个工作部件中有一个部件发生故障.关于其特例的研究可见文献[3—5].k/n(G)表决系统作为可靠性数学理论中的一类非常重要的基本模型,被广泛应用于金融系统、航空航天系统、通信系统、核安全系统等.比如,在核电站系统中,反应堆保护系统由n个保护装置组成,只要有任意的k个及以上的保护装置符合保护触发条件,系统便发出保护动作以保护三大核安全屏障(燃料包壳、一回路压力边界和安全壳)的完整性.这里的反应堆保护系统可看作是一个k/n(G)表决系统.
一些对经典的k/n(G)表决可修系统的研究可见文献[6—9].这些文献使用随机过程理论与方法讨论了系统的可用度、系统的故障频度、系统首次故障前的平均时间等可靠性指标.Zhang等[10]研究了马尔可夫型k/n(F)表决可修系统,即(n-k+1)/n(G)表决可修系统,其中部件修复如新,修理设备修复不如新.作者利用几何过程理论、排队论方法和向量马尔可夫过程理论给出了系统的可用度、故障部件的平均等待修理时间、修理设备空闲的概率等相关指标以及数值结果.另外,Krishnamoorthy等[11-13]又将各种维修策略,如D—策略,T—策略或者N—策略引入到k/n(G)表决系统的研究中,并给出了相关可靠性指标的表达式和数值结果.在文献[13]中,作者考虑的N—策略维修规则是这样的:当系统中故障部件数累积到预先设定的N值时,修理工才开始修理故障的部件,一直持续到系统中没有故障部件为止.然后,修理工转入空闲状态直到下一次系统中累积故障部件数达到N值时才又开始转入修理状态.随后,Wu等[14]研究了N策略,修理工多重休假和修理设备可更换的k/n(G)表决可修系统.利用马尔可夫过程理论和矩阵分析方法,作者得到了一系列系统可靠性指标的表达式.在此基础上建立了系统长时间运行下的利润函数,并数值给出了最优解.更多关于k/n(G)表决系统的工作可见文献[15—19].最近,付永红等人[20]研究了一个具有两水平修理策略的机器维修模型,即1/n(G)表决系统.使用补充变量法,作者获得了稳态下系统中故障机器数的概率分布,以及相关指标的表达式和数值结果.
受文献[13,20]的启发,本文考虑具有两水平(r,s)修理策略的k/n(G)表决可修系统.这种修理策略的本质在于通过对阈值的事先设定来合理有效地指派普通修理工或者熟练修理工对故障部件进行修理.与之前的k/n(G)表决可修系统模型相比较,这种修理策略的特点是:工作部件故障后并不立即对其进行任何修理,而是等到故障部件累积到事先设定的低阈值r时,才指派普通修理工进行修理.如果普通修理工在修理过程中进展不顺利,故障部件数持续增加到高阈值s时,系统性能受到严重影响时,将立即指派熟练修理工去接替普通修理工对故障部件进行修理,以尽快恢复系统的性能.利用马尔可夫过程理论和分析方法,讨论了系统可用度、故障频度以及系统首次故障前的平均时间等可靠性指标,并给出了相关指标的表达式和数值结果.
2 两水平修理策略的k/n(G)表决可修系统
本文研究的两水平修理策略的k/n(G)表决可修系统的模型描述如下:
1)系统由n个同型部件组成,当至少有k(1≤k≤n)个部件同时工作时,系统才正常工作.当故障部件数等于n-k+1时系统就故障,在系统故障期间,剩余的k-1个正常部件不再发生故障.
2)系统中每个部件的工作寿命X服从负指数分布F(t)=1-e-λt,0<λ<∞,t≥0.当工作部件发生故障时,系统将根据两水平(r,s),0≤r≤s≤n-k+1,修理策略指派相应的修理工对其进行修理.如果系统中故障的部件数小于r值时,系统暂不指派修理工修理故障部件.如果系统中故障的部件数达到r值时,立即指派普通修理工对故障部件进行修理.若普通修理工的修理工作顺利,r个故障部件及其后的故障部件修理完毕,则普通修理工撤出系统.若普通修理工的修理工作不顺利,系统中故障部件数持续增加到s值时,系统则立即指派熟练修理工对故障部件进行修理.当系统性能好转,故障部件数小于s时,熟练修理工撤出系统,原先的普通修理工进入系统继续修理,直到所有的故障部件修理完毕.如果在此期间,系统累积的故障部件数又一次达到阈值s时,则熟练修理工再次接替普通修理工进入系统开展修理工作.
3)普通修理工的修理时间Y1服从负指数分布G1(t)=1-e-µ1t,0≤µ1<∞,t≥0.熟练修理工的修理时间Y服从负指数分布G(t)=1-e-µt,0≤µ<∞,t≥0.
4)系统涉及到的随机变量彼此独立.
下面建立系统状态概率满足的稳态方程组.令L(t)=i,i=0,1,...,n-k+1,表示时刻t系统中有i个部件处于故障状态(包括正在修理的部件).设

由模型描述和负指数分布的“无记忆性”可知,随机过程{L(t),J(t)|t≥0}是连续时间拟生灭过程,其状态空间为

为了后面讨论的方便,记λi=(n-i)λ,i=0,1,...,n-k.进一步,系统的状态转移图如图1所示.

图1 系统状态转移图Fig.1 State transition diagram of the system
下面给出图1中有序数对的简单说明,其中(i,0)表示系统中有i个故障部件,i=0,1,...,r-1,系统未指派修理工修理故障部件.(i,1)表示系统中有i个故障部件,i=1,2,...,s-1,普通修理工正在修理故障部件.(i,2)表示系统中有i个故障部件,i=s,s+1,...,n-k+1,熟练修理工正在修理故障部件.
定义系统的稳态概率

根据马尔可夫过程理论和系统状态转移图,系统稳态概率满足如下方程组
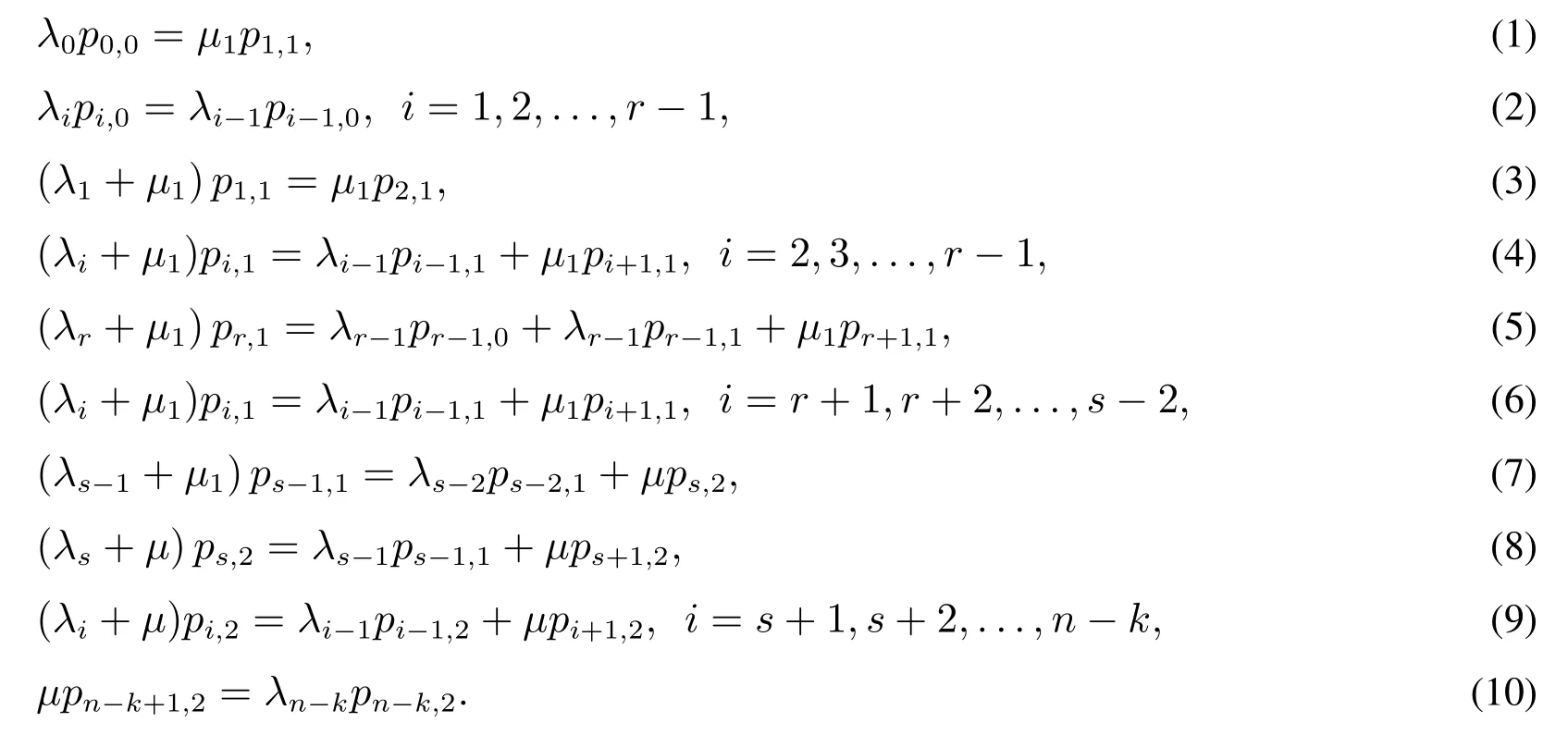
下面推导稳态概率pi,0,i=0,1,...,r-1,pi,1,i=1,2,...,s-1,pi,2,i=s,s+1,...,n-k+1的表达式.首先,由式(1)得

根据方程(2),有
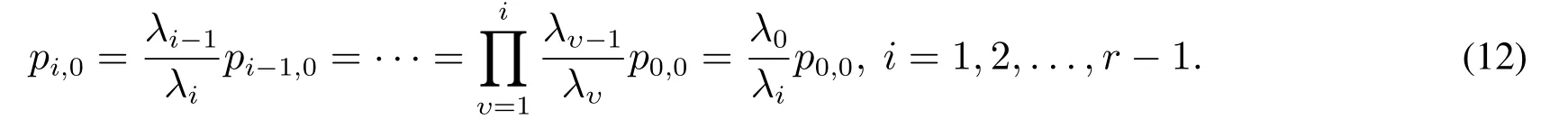
由方程(3),得λ1p1,1-µ1p2,1=-µ1p1,1=-λ0p0,0.将其代入方程(4),整理后有如下递推表达式

进一步,从式(13)可得
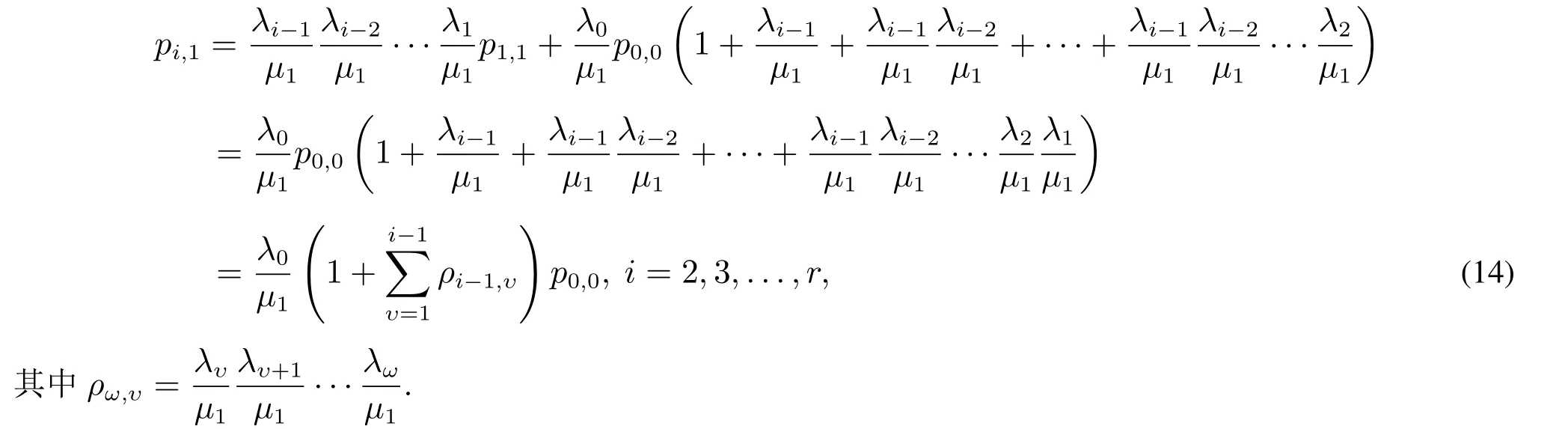
由方程(5)得

类似方程(5)的推导,由方程(6)得
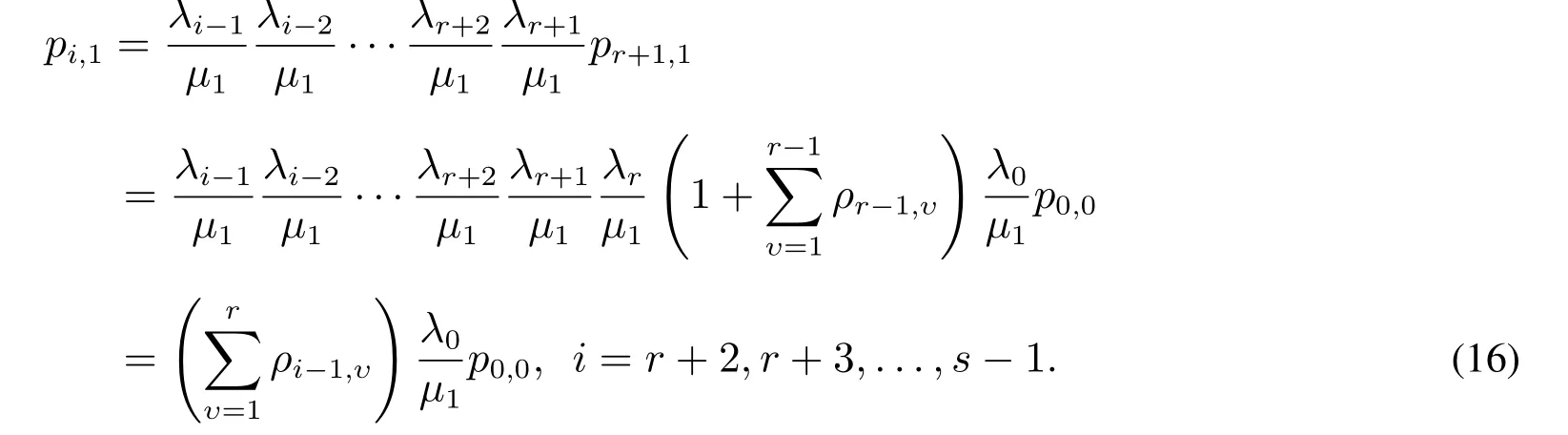
将ps-1,1和ps-2,1代入式(7),得

同样地,将ps,2和ps-1,1代入式(8),得

类似于方程(4)和方程(6)的处理,由式(9)得
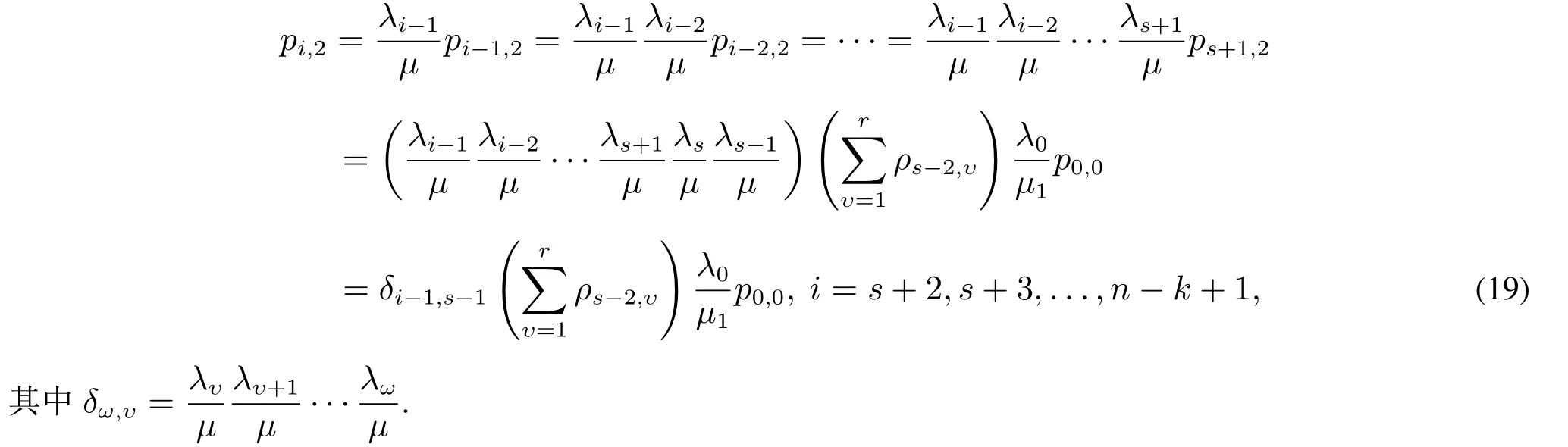
由正则性条件,所有的概率加起来为1,即
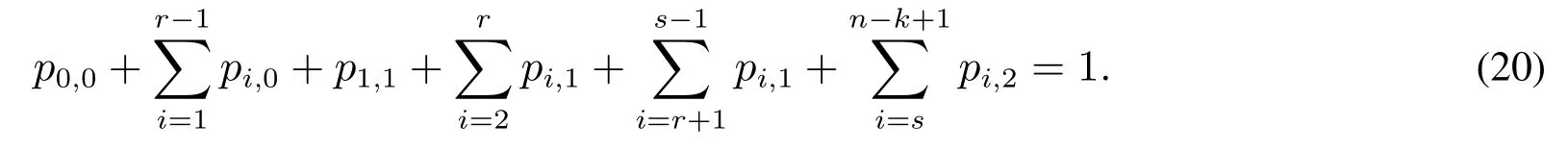
将上述各表达式代入式(20),解得p0,0=Δ,其中

至此,得到系统稳态概率分别为

下面给出稳态下系统相关性能绩效指标的表达式.
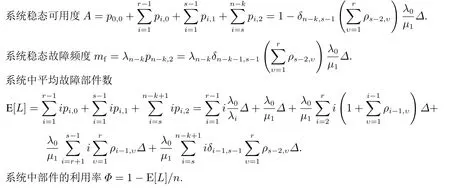

3 系统首次故障前的平均时间
定义1[21]概率分布H(x)称为(0,+∞)上具有不可约表示(α,T)的m阶位相型分布(简称PH分布),当且仅当它是一个状态空间为{1,2,...,m+1}的马氏过程的吸收时间分布,其中状态1,2,...,m都是非常返的,状态m+1为过程的吸收状态.记该过程的状态转移速率矩阵为

过程的初始状态概率向量为(α1×m,01×1),其中0表示初始时刻过程处于吸收态的概率为0.这里,分布函数为H(x)=1-αexp(Tx)e,x≥0,数学期望E[χ]=-αT-1e.
利用马氏链吸收时间理论来讨论k/n(G)表决系统首次故障前的平均时间.首先,对系统的n-k+r+1个状态按照如下的方式进行排列,即

状态(0,0),(1,0),(1,1),...,(r-1,0),(r-1,1),(r,1)...,(s-1,1),(s,2),...,(n-k,2)都是非常返的,状态(n-k+1,2)为过程的吸收状态.根据PH分布的定义可得此过程的转移速率矩阵为

因此,本文讨论的k/n(G)表决可修系统首次故障前的平均时间
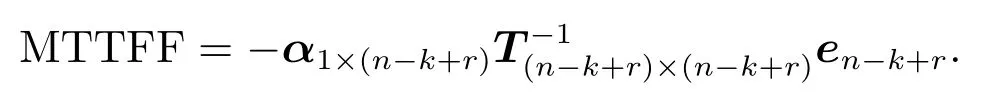
4 数值例子
算例1本算例以某地区的手机通信网络为例来分析系统相关可靠性指标随系统参数变化的情况.假设有5个传输塔就能基本满足这一地区的手机通信,但管理者为了提高通信的质量和满足不同顾客的需求,往往会多安装几个传输塔,比如18个.于是,这一地区的通信传输系统就是5/18(G)表决系统.在运行过程中,若故障的传输塔数量小于 4个时,由于对通信并不会造成实质性的影响,故暂不指派技术人员(即修理工)去修理故障传输塔.若故障的传输塔数量达到4个时,此时可能会引起通信不畅,这时管理者立即指派普通修理工对故障传输塔进行修理.在此期间,若故障的传输塔数量持续增加到12个时,通信将受到严重干扰,则立即指派熟练修理工对其进行修理.传输塔的工作寿命服从参数为λ的负指数分布,普通修理工和熟练修理工对故障传输塔的修理时间分布服从参数为µ1和µ的负指数分布.选取参数λ=0.4,µ1=2.5,µ=3.5.利用MATLAB编写相应的数值计算程序,所得结果分别见表1,表2和图2,相关数值结果保留到小数点后8位.

表1 5/18(G)表决系统稳态概率分布及相关指标的数值结果Table 1 Steady-state probabilities and performance measures of5/18(G)system
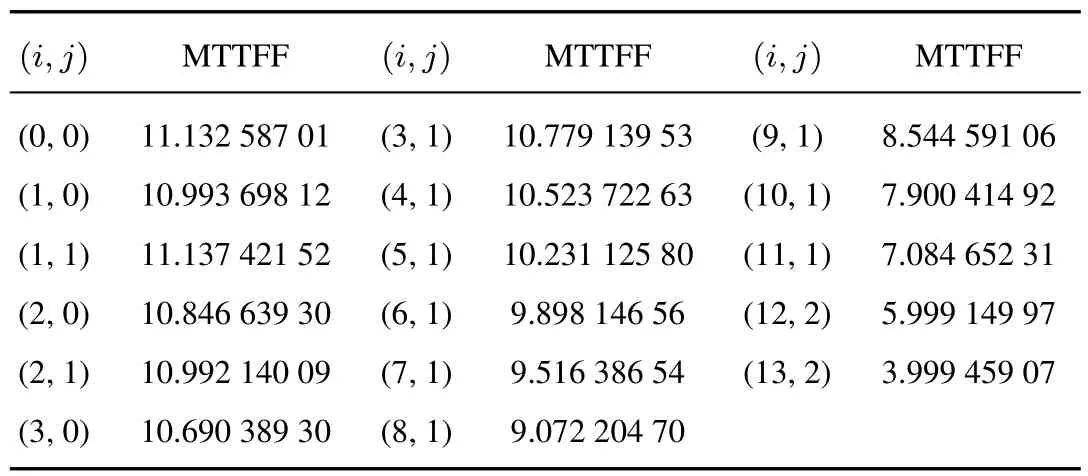
表2 不同初始条件下5/18(G)表决系统首次故障前的平均时间Table 2 MTTFF of 5/18(G)system under different initial conditions
表1给出了系统稳态概率分布及相关可靠性指标的数值结果.表2给出了在不同初始条件下系统首次故障前的平均时间的数值结果.从表中可看出开始时刻系统中故障部件数越多,其MTTFF的值就越小,这与实际情形相吻合.
图2描绘了在不同的部件故障率λ和维修阈值s下,A,mf,E[L]和Pe的数值结果.从中可看出,随着λ的增大,即工作部件越容易发生故障,系统可用度逐步减小,而故障频度、平均故障部件数和熟练修理工繁忙概率逐渐增大.另一方面,当λ取值给定时,s值越小,熟练修理工越早进入系统修理故障部件,则系统可用度明显增大,而故障频度、平均故障部件数变小.正由于较早进入系统,故熟练修理工繁忙的概率相应地增大了.

图2 不同参数λ和s下5/18(G)表决系统可靠性指标变化曲线Fig.2 System performance measures of 5/18(G)system versus(λ,s)
算例2令k=1,则k/n(G)表决系统退化为经典的机器维修模型.付永红等[20]获得了机器模型稳态下故障机器数的概率分布及相关指标的递推表达式.为了验证本文表达式的正确性,取文献[20]的相关参数值:n=12,λ=0.1,µ1=0.5,µ=0.7,r=4,s=8.利用MATLAB编写相应的数值计算程序,得到的具体结果见表3.从表中可看出,本文表达式的数值结果与文献[20]的表达式的数值结果吻合.

表3 1/12(G)表决系统稳态概率分布及相关指标的数值结果Table 3 Steady-state probabilities and performance measures of 1/12(G)system
算例3令r=1,µ1=µ,则模型退化为经典的k/n(G)表决可修系统.曹晋华等[2]利用马尔可夫分析方法得到了此系统稳态下的可靠性指标的表达式

为了说明本文所得表达式的正确性,选取k=3,λ=0.55,µ1=µ=2.5.通过MATLAB编写数值计算程序,得到具体的的数值结果见表4.从表中可以看出,本文表达式的数值结果与文献[2]给出的表达式的数值结果吻合.
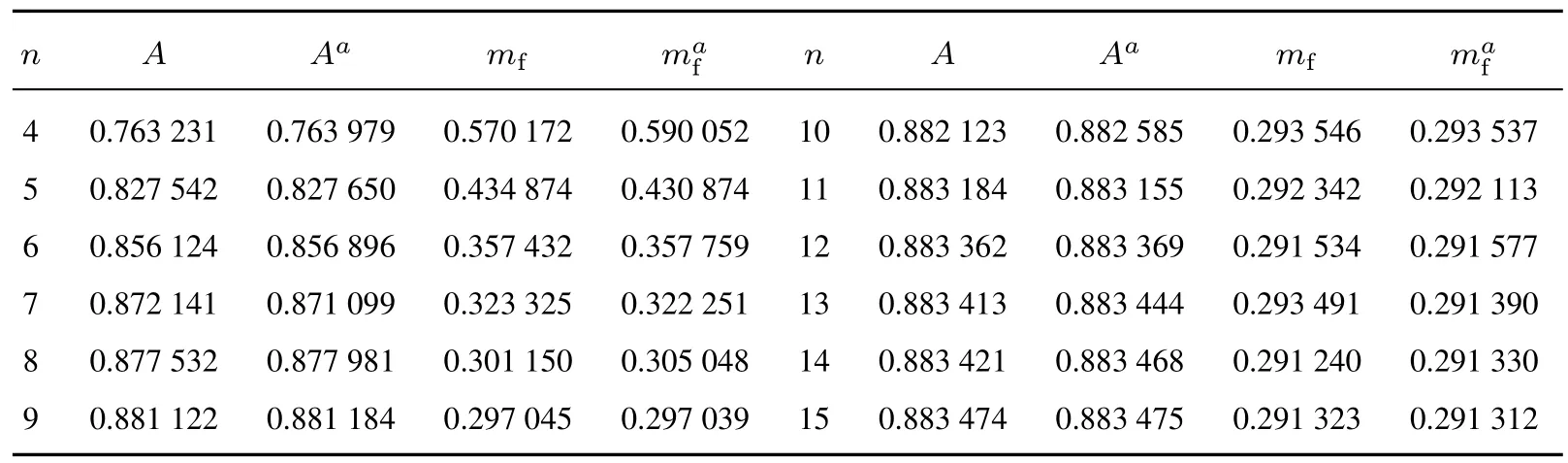
表4 不同n值下k/n(G)表决系统稳态可靠性指标的数值结果Table 4 System reliability measures for different values ofn
算例4本算例通过Monte Carlo仿真对本文解析结果的正确性进行验证.取k=2,n=3,µ1=2.0,µ=3.5,r=1,和s=2;λ的取值从0.5到1.0,利用MATLAB编写相应的程序,运行500 000次后所得结果见图3和表5.这里,相对误差=|理论结果-仿真结果|/理论结果.从表5和图3可知本文表达式是可信的.

图3 不同参数λ下系统可靠性指标变化曲线Fig.3 System reliability measures for different values ofλ
5 结束语
本文研究了两水平修理策略的表决可修系统,利用马尔可夫过程理论,建立了系统稳态概率满足的方程组,并采用求解经典生灭过程的思路获得了一系列刻画系统性能绩效指标的表达式.在此基础上,通过MATLAB软件编程给出了在不同条件下系统相关可靠性指标的数值结果.最后,通过Monte Carlo数值仿真和对特殊情形的讨论数值验证了所得表达式的有效性.在今后的研究中,引入修理工休假策略(多重休假,单重休假)是一个值得考虑的问题.
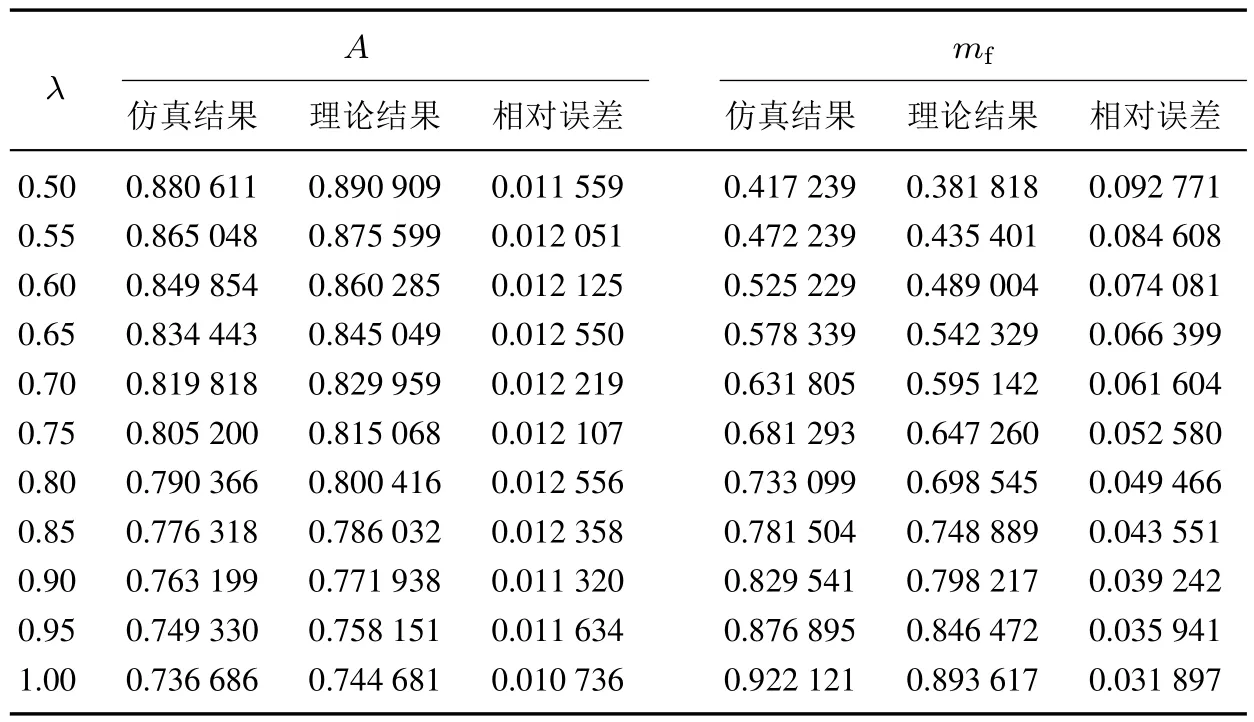
表5 不同λ值下系统稳态可靠性指标的数值结果Table 5 System reliability measures for different values ofλ
