小角法在基坑水平位移监测中的应用及精度分析

周挺挺

(中交三航局兴安基建筑工程有限公司,上海201315)

0 引 言

目前,在建筑工程测量中,全站仪的应用越来越多,一定程度上代替了经纬仪和水准仪,常用于基坑监测[1]和各类施工测量[2]。随着仪器制造技术发展,高精度全站仪不断涌现,如徕卡TS30型全站仪,其测角精度达0.5 s,测距精度达0.6 mm+D·10-6m,对提高建筑工程中各类测量精度具有重要推动作用。近年来,全站仪测量精度研究多集中于仪器精度和应用精度[3-6]。在小角法精度研究方面,多侧重于仪器选择、施测技术研究。关于全站仪小角法水平位移监测精度分析并不多,这造成小角法位移监测精度分析不足,许多分析成果还停留在过去十几年间经纬仪小角测绘阶段上[7-8]。在全站仪精度日益发展背景下,小角位移监测所能达到的精度尚没有理论分析与实验验证。基于徕卡TS30型全站仪水平位移观测数据,本文在理论上分析了小角法的测量精度,并在位移监测中评定了全站仪小角法水平位移监测精度,结果发现,该方法精度较高,是一种快速高效的水平位移观测方法。

1 理论精度分析

1.1 测量原理

小角法位移监测是测定建筑物监测点沿某基线偏移的位移量,其实质是一种近似计算方法。将测站点到监测点多次测量距离视为相等,将位移量视为弧长,可构造小角图(图1)。

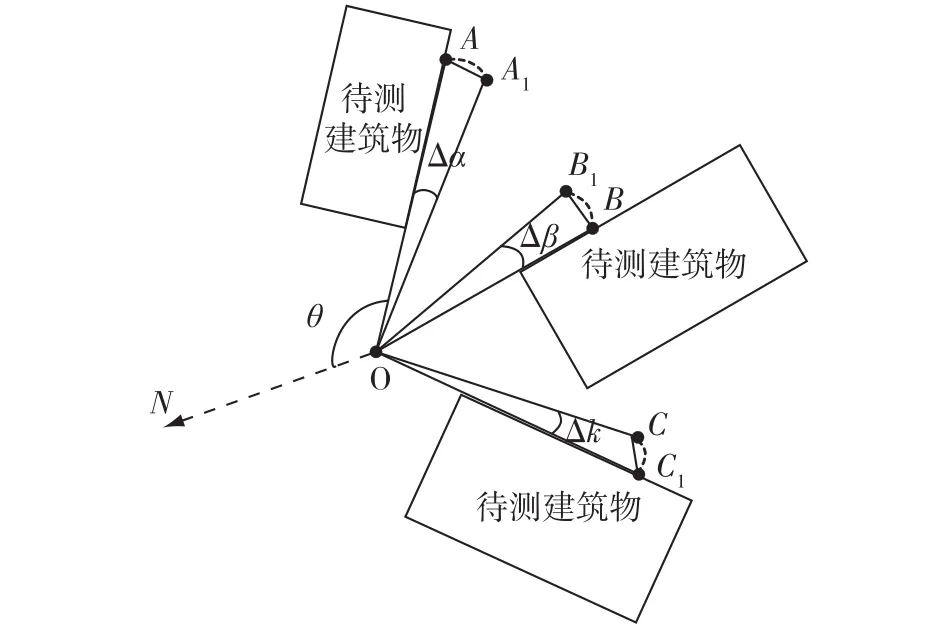
图1 小角法测量原理

根据弧长与半径的几何关系,可依次推算相邻观测期小角增量Δα、Δβ、Δκ所对应的位移偏移量AA1、BB1、CC1,以B点两次偏移量δ计算为例,如式(1)所示,其中ρ=206 265″,D为测站到监测点的水平距离,如果是多次观测,可视为各次观测值相同。

1.2 误差分析

1.2.1 角度误差分析

由式(1)可知,影响小角测量精度的因素有角度和距离两种。由于二者在观测中是独立的,根据误差传播定律,对式(1)变量进行微分,得到小角法位移误差计算公式:

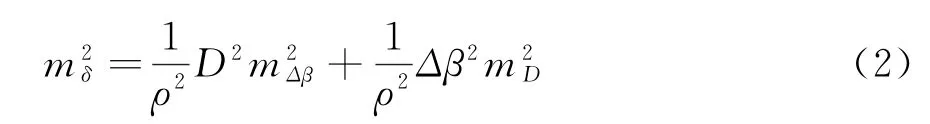
Δβ是两次观测水平角之差,设观测误差为mβ,再由误差传播定律易知。而mβ受多种因素影响,主要包括观测误差、仪器对中误差、目标偏心误差、仪器误差和外界条件。其中影响较大的是观测误差、仪器对中误差和目标偏心误差,仪器误差和外界条件误差影响较小,且属偶然误差,难以定量,研究中此项被忽略。

设观测误差为m u,仪器对中误差为m e,目标偏心误差为m p,则。根据徐汉涛[7]的理论,在顾及最不利因素条件下,分别计算m u、m e和m p最大值,将计算的代入,最终可得,结果如式(3)所示。其中m v为全站仪一测回测角中误差,n为测回数,D'为测站点到后视点距离,e为对中偏心距,e'为目标偏心距。

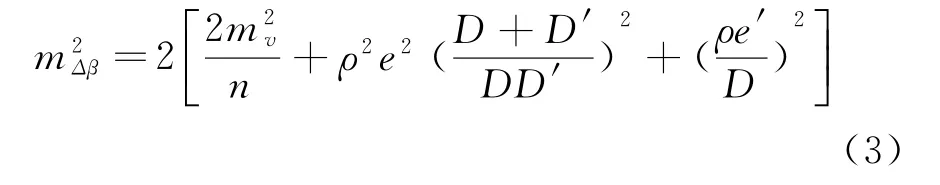
1.2.2 距离误差分析

全站仪小角法测距误差与传统测距误差不同。传统钢尺量距采用的是相对误差方法,设测距误差为m D,则m D=k D,k为测距相对误差,一般在基坑监测中取1/10 000以上的精度。由于全站仪以标称精度表示测距精度,故可设全站仪测距精度为m D=a+b·D。其中,a为固定误差,b为比例误差。将式(3)代入式(2),将m D=a+b·D也代入式(2),得到式(4)。式(4)为小角法位移误差计算公式,在运用全站仪小角测绘时,m v就是全站仪测角精度,其他参数的意义与前述相同。

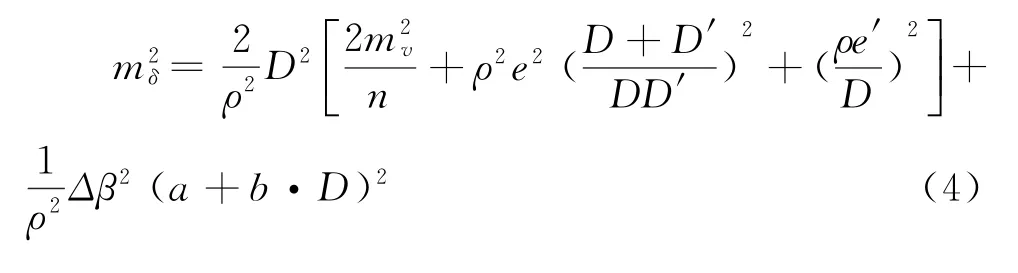
2 精度分析

式(4)的参数较多,大致分为4类:① 纯常数,包括ρ与n,其中ρ值为206 265″,n可取1或2,本例中由于仪器精度较高,n选1;② 仪器参数,包括m v、a、b,可从仪器厂商处获得;③ 全站仪观测值D、D'、Δβ,通过观测获得;④ 经验值e、e',在最不利条件下,二者可设为最大值3 mm。本工程采用的徕卡TS30全站仪,测角精度为0.5″,测距精度为0.6 mm+D·10-6m,因此式(4)各参数的取用值如下所示(表1)。

表1 小角法位移误差参数配置

3 监测实例

3.1 监测工程

研究项目为珠海市某高层建筑基坑,场地内拟建造一栋35层高的建筑物(地面以上高度172.50 m),设置4层裙楼(地面以上高度20.40 m),设置4层地下室(地下室底板顶标高-15.80 m,开挖深度为-16.90 m)。拟建场地基坑呈近似矩形,基坑各边基本为平行红线内移10～15 m,长100.67 m,宽43.42 m。工程布设水平位移监测点8个,北部3点,编号为N-S1、N-S2、N-S3;东南2点,编号为SE-S4、SE-S5;南部1点,编号为S-S6;西南1点,编号为SW-S7;西部1点,编号为W-S8。工程共布设6条基线,12个观测点,其中6个为测站点,编号为1—6,6个为照准点,编号为G1—G6,对应基线为 G1-1、G2-2、G3-3、G4-4、G5-5、G6-6。同时布设6个检核点J1—J6,目的是检核6条基线的稳定性(图2)。项目要求监测精度不低于三等,监测频率为:开挖深度小于5 m时,1次/2 d;5～10 m时,1次/d;大于10 m时,2次/d;地板浇筑后,7 d以内,2次/d;7～14 d,1次/d;14～28 d,1次/2 d;多于28 d时,1次/3 d。报警阈值要求为30 mm(或3 mm/d),当监测值超过报警值或连续3 d超过该值的70%时,及时报警。

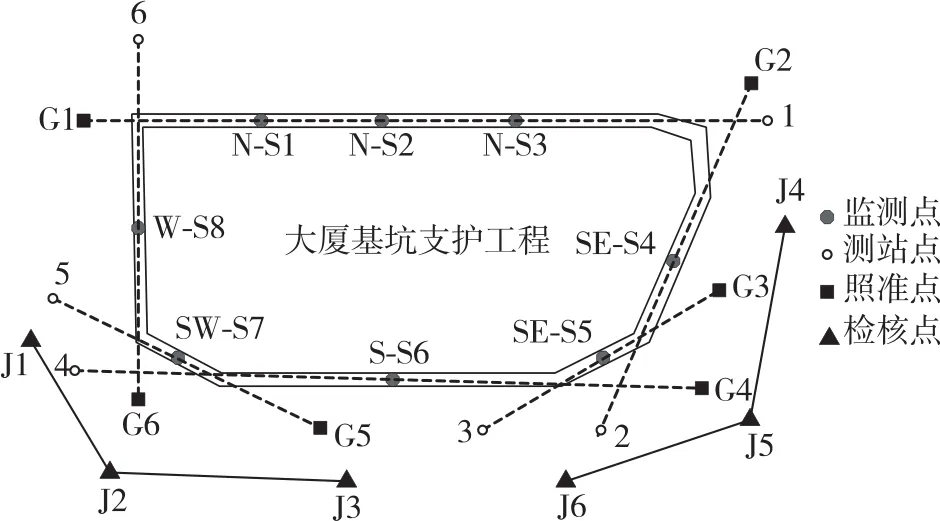
图2 水平位移监测点分布图

3.2 位移分析

水平位移监测采用徕卡TS30全站仪,测角精度0.5″,测距精度0.6 mm+D·10-6m,自2012年12月29日观测至2015年7月15日为止,总计观测119次,将各期观测值累计位移变化率绘制曲线图(图3)。

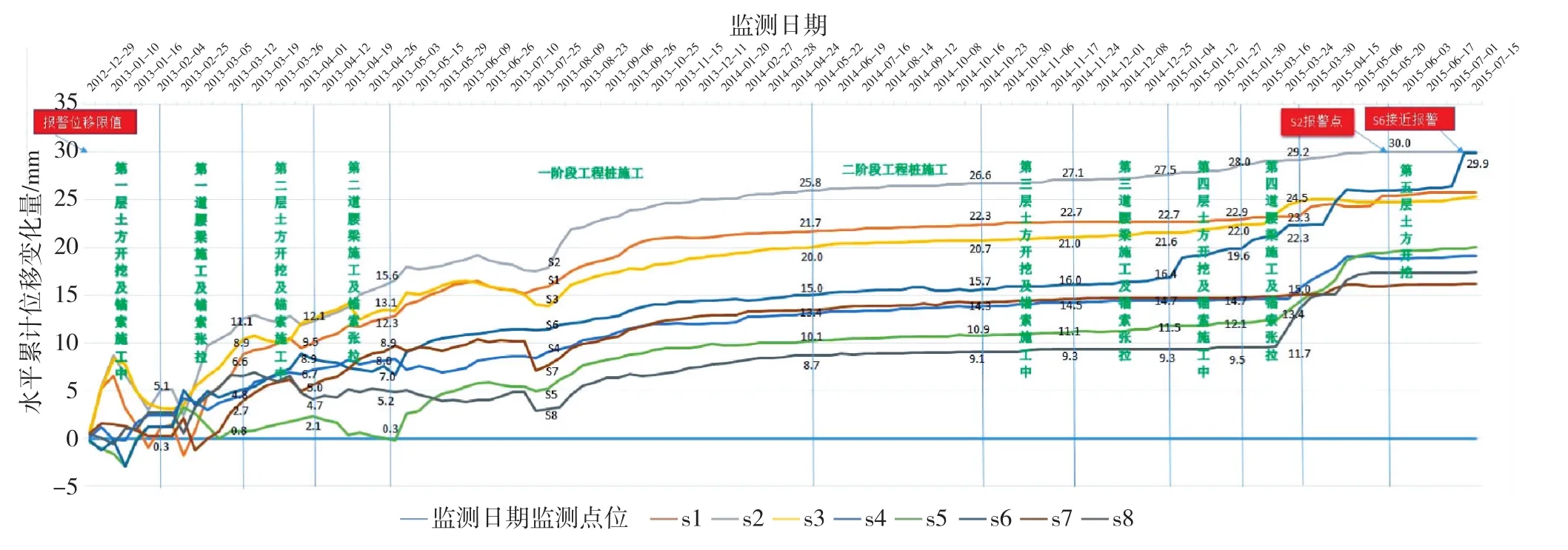
图3 累计位移量变化图

图4 N-S2与S-S6累计位移值图

图3中,N-S2和S-S6点变形值接近警报阈值,因此对其进行基坑边界线内外侧位移分析。利用式(1)计算相对基坑外侧和内侧位移(垂直于基坑边线),并规定沿基坑外侧方向为负值,沿基坑内侧的方向为正值,绘制N-S2和S-S6点各期位移累计图(图4)。

分析图4(a)可知,N-S2水平位移变形均向基坑内侧,外侧没有位移,当期和累计变形值较大;观测中后期,位移量增量越来越大,位移累计图呈现“鼓肚”状态,到最后10期,累计位移量为29.9 mm,已经接近于报警阈值。根据图4(b),S-S6前几期有基坑外位移,最大值为3 mm,之后全部为基坑内向位移,位移量和累计位移量也随之增加,但幅度较N-S2点小,到最后4期,累计位移量达到29.8 mm,也接近于警报值。

3.3 误差分析

取表1所设的参数对8个水平位移监测点进行观测,利用D、D'、Δβ观测值计算各点第二期位移误差(表2)。

表2 小角法位移监测精度/mm

从表2不难看出,观测值相对于误差的影响可忽略不计,位移误差为9.5 mm,根据《建筑变形测量规范》(JGJ 8—2016),三等位移精度为±10.0 mm[9],故本案中的位移精度已达到三等标准。此外,通过对式(4)进行分析不难发现,对精度影响最大因素是e、e'。在本例中,计算采用最大值,二者均取3 mm,根据式(4),若二者取2 mm,mδ=4.0 mm;若二者取1 mm,mδ=2.0 mm,根据经验,控制在2 mm内较容易,即小角法水平位移误差控制在2 mm易于实现。因此,提高小角位移监测精度的首要任务是减少对中误差和目标偏心误差;而选用仪器和选择施测方法则对精度影响不大,不是首要考虑的因素。

4 结 语

(1)基于误差理论,对水平位移监测所达到的精度进行了评定。

(2)通过监测实验发现,全站仪小角法水平位移监测具有施测简单,易于可视化分析的优点。同时在最不利条件下对位移误差进行保守计算,结果表明,水平位移精度达到三等监测要求。由实验数据推导发现对中误差和目标偏心误差是造成位移误差的主要因素,如果这两项误差控制得当,可大幅提高水平位移监测精度。因此,在小角法观测中仪器应严格对中,需精确照准,必要时要采用照准设备保证照准精度,同时要提高仪器观测者技术水平和工作态度,将对中和照准偏心误差控制在较小范围内,保证观测精度。

[1]刘沛.自动化全站仪在高层建筑基坑变形监测中的应用[J].测绘与空间地理信息,2011,34(3):239-241.

[2]马亮.广州国际会展中心预应力张弦式桁架施工测量[J].施工技术,2003,32(5):28-29.

[3]郭宗河,郑进风.全站仪面积测量及其精度分析[J].测绘通报,2002(3):30-31.

[4]蓝善勇.全站仪在渠道测量中的精度分析及其应用探讨[J].测绘通报,2012(4):75-78.

[5]周俭清.全站仪对边测量原理及精度分析[J].北京测绘,2005(3):50-52.

[6]周显平.全站仪三角高程测量及精度[J].辽宁工程技术大学学报:自然科学版,2011,30(5):717-720.

[7]徐汉涛.小角法水平位移观测的误差分析[J].南通工学院学报,2001,17(3):37-40.

[8]张宏志.小角法在矿区建筑物水平位移监测中的应用[J].煤炭与化工,2014,37(3):121-122,149.

[9]中华人民共和国住房和城乡建设部.建筑变形测量规范:JGJ8-2016[S].北京:中国建筑工业出版社,2016.