相位相关辅助的重复纹理区域特征跟踪匹配

闫 利， 龚 珣， 谢 洪

(武汉大学测绘学院,武汉 430079)

0 引言

在城市三维重建过程中，广泛使用移动测量车搭载CCD相机的方式获取街道场景的影像。随着这种数据采集方式的日趋成熟，获取的数据量越来越多，为进一步挖掘数据的利用价值，研究人员开始关注如何对街道序列影像进行精确定向以及利用街道序列影像如何对街道三维场景进行重建的问题。而在对街道序列影像进行影像定向以及三维重建的过程中，寻找同名特征点已成为一个挑战性问题。以往为了寻找同名点，研究人员提出过大量特征匹配算法，其中Lowe[1]提出的尺度不变特征变换(scale-invariant feature transform,SIFT)算子是公认的最为出色的特征提取与描述算子，但利用该算法进行特征匹配的实时性较差，故此后有很多研究人员对SIFT算子进行了改进[2-4]。而移动测量车所获取的街道序列影像有一个突出的问题，那就是影像中存在大量的规则重复纹理，采用特征描述的方法很难将其区分开来； 利用上述方法对街道序列影像进行特征匹配时，在重复纹理区域会造成大量误匹配点。因此，如何解决重复纹理区域特征的匹配问题，已成为街道序列影像定向以及三维重建的关键之一。针对具有重复纹理的户外自然场景特征跟踪问题，刘伟等[5]在随机树算法的基础上，提出了一种内点回收算法，通过构造匹配点集，利用特征纹理在影像中的空间信息，从集合中选择最佳匹配点来提升匹配效果； 但该算法只适用于解决具有少量对称重复纹理区域的匹配问题。针对重复纹理区低空影像匹配问题，何海清等[6]提出利用相位相关预测同名点在平移、旋转和尺度上的遍历范围，在遍历范围内检测角点，并利用相关系数来匹配同名点； 但因车载序列影像的摄影距离很近，导致相邻影像之间的投影变形十分严重，使用该方法在整体相位相关方面可能会得到错误结果。针对上述问题，本文提出了一种利用分块相位相关辅助的KLT(Kanade-Lucas-Tomasi)跟踪方法来解决街道序列影像重复纹理区域的匹配问题。首先，利用分块相位相关将原始影像分割成景深趋于一致的子区域，并在子区域上对同名点进行预测； 然后，以相位相关预测的初始位置为中心，利用KLT算法对影像中的角点进行精确跟踪； 最后，利用核线约束，通过随机抽样一致性(random sampling consensus，RANSAC)方法剔除错误匹配点，完成跟踪匹配。

1 重复纹理区域特征匹配

在移动测量系统获取的街道序列影像中，建筑物立面占有相当大的比例，而通常建筑物立面含有大量的规则重复纹理。利用特征匹配的方法对此类影像进行匹配时，容易造成大量的误匹配，严重影响后期的影像定向以及三维重建。针对此问题，本文提出一种利用相位相关算法辅助KLT对角点进行跟踪，从而实现特征匹配的算法。首先，在整体上利用相位相关将待匹配的影像对进行粗配准； 然后，使用KLT算法从影像中提取局部角点特征并进行跟踪匹配。本文算法技术流程如图1所示。

1 本文算法技术流程Fig.1 Technical flowchart of algorithm proposed in this paper

2 基于分块相位相关的初始位移获取

相位相关算法对噪声具有鲁棒性，并且处理结果比较稳定，适用于对影像进行整体配准来获取全局的位移信息。但是，相位相关并不适用于影像之间同时存在旋转和缩放等变形的情况。街道序列影像由于摄影距离近，影像之间存在较大的投影变形，使用相位相关算法尽管在全局可获得最佳配准，但局部区域的配准结果并不理想。为了使局部区域配准精度满足KLT跟踪所需要的初始条件，在相位相关的基础上，对影像进行子区域划分； 然后在每一子区域再次相位相关，当子区域划分达到一定程度后，每一局部区域的相位相关精度就能够满足KLT跟踪的要求。

2.1 相位相关算法原理

基于傅里叶变换相位相关算法的主要思想是： 利用傅里叶变换(Fourier transform)将空间域表示的影像变换到频率域，在频率域中进行相关运算后，再将结果利用逆变换变换回空间域来求取2景影像之间的平移量。用f1(x,y)和f2(x,y)分别表示2景影像，假设影像之间存在平移d(dx,dy)，其平移关系可表示为

f2(x,y)=f1(x-dx,y-dy)。

(1)

将式(1)左右两边分别进行傅里叶变换，可得到2景影像在频率域的关系，即

F2(u,v)=e-j2π(udx+vdy)F1(u,v)，

(2)

式中j为虚数常量，等于-1的平方根。

根据式(2)得到2景影像的互功率谱的表示形式，即

(3)

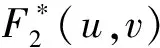
2.2 分块相位相关算法

通过分块的方法，使每一子区域相位相关的精度均满足KLT跟踪的需求，是此阶段相位相关的目的。结合街道序列影像数据的特征，综合运用影像边缘提取、影像2幂划分和相位相关，在达到所需精度的同时，也使效率达到最高。分块相位相关的流程如下： ①提取参考影像与待配准影像的边缘； ②对边缘影像整体进行相位相关，求取初始位移量； ③以上次相位相关得到的位移量为基础，将影像分割成多块子区域； ④在每个子区域再次利用相位相关求取位移量； ⑤重复步骤③和④，直到子区域的配准精度满足下一步KLT跟踪的要求。分块相位相关配准结果如图2所示。从图2(d)中的对比可以看出，不同的景深导致3块区域在相邻影像中的视差变化差异很大。如果单纯采用相位相关在整体上求解位移量，并不能得到很好的结果。图2(e)中显示，采用分块相位相关算法，能够对每一部分都配准得比较好。但是，从图2(e)中也可以看到，由于分块并没有考虑影像的结构特征，蓝色部分的相位相关仍存在问题； 然而与整体相位相关只能得到一个位移相比，分块相关结果整体精度更高，且满足KLT跟踪的要求。

图2分块相位相关配准结果

Fig.2Registrationresultsofblockphasecorrelation

2.2.1 影像边缘提取

街道序列影像的深度不连续以及拍摄的距离较近，导致相邻影像不同区域的视差变化很大，因此采用分块相位相关的方法可以较好地解决这一问题。但在实验处理阶段发现，影像中灰度剧烈变化所形成的边缘导致相位相关的结果仅在这些边缘附近对齐，而不是整体上的最优。经过分析表明，影像中的建筑物表面纹理灰度强度变化相对微弱，在功率谱上会形成小的峰值，而灰度剧烈变化的边缘区域在影像功率谱上则会形成高振幅的波峰，从而导致相位相关过程中灰度变化剧烈的区域占很大权重。

为了抑制灰度强烈变化边缘区域在相位相关中的权重，增强灰度变化相对较弱的重复纹理区域的权重，本文采用了一种基于轮廓的相位相关算法。张静等[7]在研究全景影像自动拼接算法时，使用了一种基于轮廓的相位相关技术，提高了相位相关的鲁棒性和效率。

考虑到本文的目的是在保留低对比度区域的基础上抑制高对比度区域，如果采用Canny边缘检测等完整的边缘检测算法会比较耗时，而且相位相关也不需要连通的边缘信息，因此本文采用了一种简单的影像轮廓提取方法： 首先，获取影像在水平和垂直方向的梯度图； 然后，设定适当的阈值，对梯度图进行二值化，形成影像的轮廓。利用上述方法生成的轮廓影像保留了原始影像主要的频率信息，同时抑制了因亮度不同导致的影像差异。

2.2.2 基于2幂的影像分块

将影像从空间域变换到频率域的过程中，使用了快速傅里叶变换(fast Fourier transform，FFT)。在FFT变换中，维数N必须是可以分解的较小数的乘积，而且当N是2的幂数时，效率最高、实现最简单。根据这一原理，张世阳等[8]运用2幂子图像加快图像匹配的效率； 罗如为等[9]应用这一方法加速全景影像的拼接。依据该方法，首先，将影像适当变形，得到2幂子影像； 然后，进行相位相关，在分块阶段以1/2作为分块的系数，使分块影像为2幂对齐。

3 基于KLT的特征点匹配

3.1 KLT算法原理

KLT 跟踪算法最早由Lucas等[10]提出，后又由Shi等[11]和Bouguet[12]进行了完善。该算法主要的思想是将传统的滑动窗口搜索法变为一个求解偏移量的过程： 考虑序列影像中相邻2景影像I(x,y)和J(x,y)，假设之间的微小相对位移为d(x,y)，以影像中某一特征点为中心开辟一个小窗口W，以2个窗口之间的灰度差平方和作为代价得到式(4)，即

(4)

式中：x=[x,y]T，为特征点的位置；d=[dx,dy]T，为特征点在2景影像之间的平移量；ω(x)为权值函数，一般设为常数1；W为跟踪的窗口范围。

将式(4)对d求偏导数并在x处一阶泰勒展开，得到

(5)

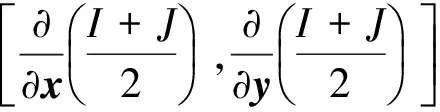
(6)

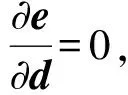
(7)

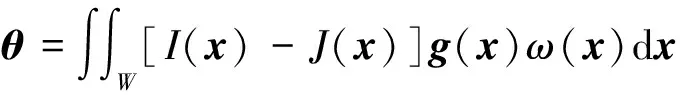
Zd=θ。

(8)

为了能够求得2个窗口之间的偏移量d，需要保证Z可逆。此时偏移量d可通过式(9)求出，即

d=Z-1θ。

(9)

3.2 相位相关辅助的KLT特征跟踪

KLT算法作为广泛使用的视频稀疏跟踪算法，具有计算简单、效率高且能够达到亚像元精度的优点。但由于视频数据获取的时间分辨率较高，视频跟踪算法通常假设视频流里相邻2景影像获取的场景所发生的变化属于微小变化，表现在影像中的特征点相对位置只发生微小位移，因此跟踪可以在小范围内很好地进行。但直接将KLT应用在本文的匹配场景中并不合适，因为移动测量设备所获取的街道序列影像的时间分辨率远低于视频，相邻影像之间的微小位移假设已经不再成立； 而且当影像中的特征角点具有明显可区分性时，尽管通过分层KLT跟踪[12]的方法可以扩大跟踪范围，但街道序列影像中存在的重复纹理会导致跟踪范围扩大后算法容易收敛到错误的角点上。因此，本文采用的相位相关辅助KLT的思想是利用相位相关算法将影像对进行粗配准，使其满足KLT跟踪的条件。换言之，就是限制KLT的跟踪范围，使其从可靠的初始位置开始搜索最佳匹配点。具体的步骤如下： ①从参考影像中提取特征角点； ②根据参考影像中角点坐标和相位相关获取的平移量，在待匹配影像中预测对应点的坐标； ③以预测坐标为中心，利用KLT算法在待匹配影像中给定范围内寻找最佳匹配点。

4 实验结果与分析

采用移动测量车获取的某一地区序列街景影像进行实验，原始影像大小为2 058像元×2 456像元。考虑到原始影像中有非常大的部分为路面数据，这部分数据变形严重，无法进行有效匹配，因此在实验中截取原始影像的上半部作为输入影像。实验硬件平台为Intel I3-2350M，双核2.3 GHz CPU，4 G内存，软件平台为WIN10 64位系统，VS2013专业版，使用C++编程语言以及OpenCV实现本文算法以及结果显示。

图3给出其中一组影像对的实验结果，并以SIFT算法的结果作为对照。

(a) SIFT算法匹配结果(b) 本文算法匹配结果(c) SIFT核线约束剔除错误匹配后结果 (d) 本文算法核线约束剔除错误匹配后结果

图3SIFT算法与本文算法匹配结果比较

Fig.3ComparisonofmatchingresultsusingSIFTandalgorithmproposedinthispaper

4.1 匹配结果定性分析

从图3(a)可以看出，采用SIFT算法提取的特征点大量分布在纹理丰富的区域(如影像左半部以及下部文字区域)，而在影像中纹理缺乏的区域(如影像右上角的墙面部分)，SIFT算法仅能够提取到少量明显的特征。这说明了SIFT算法作为一种特征描述子，强烈依赖特征点周围的纹理特性，不适合用来解决弱纹理区域的特征匹配问题。从匹配的结果来看，在影像左半部以及下部文字区域，SIFT算法匹配结果较好； 而在影像弱纹理区域，SIFT算法虽然提取了少量明显纹理特征，但因重复纹理的干扰，仍然无法匹配到正确的特征点。

从图3(b)可以看出，本文利用Hessian角点提取算子，即使纹理缺乏，在影像中的建筑区域依然能够提取到大量的角点。从匹配结果来看，本文采用的分块相位相关算法，以特征点之间的相对位置关系作为先验信息求取最佳的匹配点，在匹配的结果上没有出现较大的位置偏差，能够较好地抵抗重复纹理的干扰。

对于影像中错误的匹配结果，采用核线约束进行错误匹配的剔除，剔除后的结果如图3(c)和(d)所示。可以看出，采用核线约束后大量的错误匹配被剔除，但在结果中仍然存在少量的错误匹配，这是由于核线约束无法剔除位于核线附近的错误匹配。对比本文算法与SIFT算法剔除错误匹配后的结果可以看出，2种算法各有优缺点，SIFT算法主要考虑特征相似性； 本文算法则主要考虑空间位置关系。另外，本文算法剔除错误匹配后，特征点明显增多，特别是在SIFT算法无法提取到特征点的弱纹理区域，本文算法得到了大量的正确匹配。如果能够将以上2种算法融合起来，同时考虑特征相似性和空间位置关系，那么得到的匹配效果应该会更好。

4.2 统计结果定量分析

选取序列影像中3组影像对匹配的结果，对匹配的特征点数以及经过核线约束剔除误匹配后的匹配特征点数进行统计分析，统计结果如表1所示。

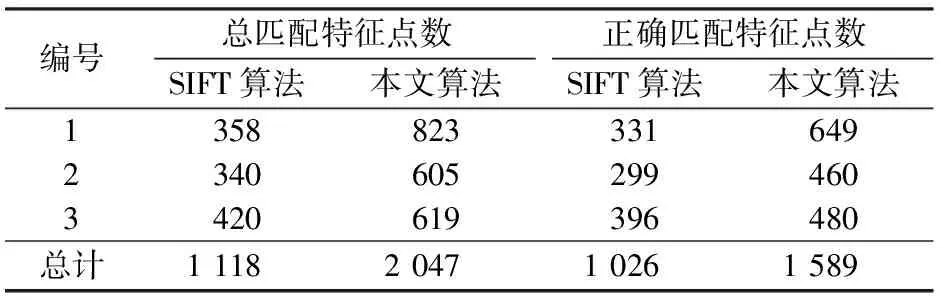
表1 SIFT算法与本文算法匹配结果统计Tab.1 Statistics of matching results using SIFT and algorithm proposed in this paper (个)

从表1中可以看出，本文算法匹配特征点总数远大于SIFT算法的匹配特征点总数。虽然本文算法所得到的错误匹配也相对较多，但是剔除错误匹配后，本文算法的正确匹配特征点数仍然比SIFT算法多。

对2种算法在实验平台上的运行时间进行了统计，统计结果如表2所示。

表2 SIFT算法与本文算法匹配时间统计Tab.2 Statistics of matching time by SIFT and algorithm proposed in this paper (s)

从表2中的运行时间统计结果来看，本文算法平均用时为4.967 s，SIFT算法平均用时为4.853 s，两者相差约0.1 s，匹配效率基本相当。

5 结论

1)传统的SIFT特征匹配算法，将影像局部转换到特征空间，在特征空间中进行匹配，没有顾及特征的空间位置关系，在重复纹理及弱纹理区域难以得到正确匹配。

2)本文提出的相位相关辅助的特征跟踪算法充分利用了特征之间的空间位置关系来进行跟踪匹配。在街道序列影像的匹配实验中，SIFT算法往往得不到足够的匹配特征点，而本文算法则取得了较好的匹配结果，这对于后续影像定向及三维重建具有重要意义。

3)本文算法过于依赖特征间的空间位置关系，有时会导致严重错误。如能结合传统特征匹配的优势，研究同时顾及特征相似性和空间位置相似性的匹配算法，将会大大提高特征匹配的效果。

4)本文使用核线约束无法剔除位于核线附近的错误匹配，如何寻找合适的几何约束条件增强核线约束、进一步剔除错误匹配，还有待进一步研究。

[1] Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.

[2] Bay H,Ess A,Tuytelaars T,et al.Speeded-up robust features(SURF)[J].Computer Vision and Image Understanding,2008,110(3):346-359.

[3] Ke Y,Sukthankar R.PCA-SIFT:A more distinctive representation for local image descriptors[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington,DC:IEEE,2004,2:II-506-II-513.

[4] Morel J M,Yu G S.ASIFT:A new framework for fully affine invariant image comparison[J].SIAM Journal on Imaging Sciences,2009,2(2):438-469.

[5] 刘 伟,王涌天,陈 靖.针对重复纹理场景的跟踪定位算法[J].北京理工大学学报,2012,32(2):189-193.

Liu W,Wang Y T,Chen J.A novel registration algorithm for repetitive texture[J].Transactions of Beijing Institute of Technology,2012,32(2):189-193.

[6] 何海清,张永军,黄声享.相位相关法辅助的重复纹理区低空影像匹配[J].武汉大学学报(信息科学版),2014,39(10):1204-1207.

He H Q,Zhang Y J,Huang S X.Phase correlation supported low altitude images matching with repeated texture[J].Geomatics and Information Science of Wuhan University,2014,39(10):1204-1207.

[7] 张 静,胡志萍,刘志泰,等.基于轮廓相位相关的图像自动拼接[J].大连理工大学学报,2005,45(1):68-74.

Zhang J,Hu Z P,Liu Z T,et al.Image automatic mosaics based on contour phase correlation[J].Journal of Dalian University of Technology,2005,45(1):68-74.

[8] 张世阳,王俊杰,胡运发.一种快速全景图像拼接技术[J].计算机应用与软件,2004,21(3):77-79.

Zhang S Y,Wang J J,Hu Y F.Development of fast panorama image mosaics[J].Computer Applications and Software,2004,21(3):77-79.

[9] 罗如为,陈孝威.360°图像序列的柱面全景拼接算法[C]//第二届和谐人机环境联合(第15届全国多媒体技术、第2届全国人机交互、第2届全国普适计算)学术会议论文集.杭州:中国计算机学会,2006:95-101.

Luo R W,Chen X W.The algorithm of cylindrical panorama mosaicing for 360° image sequence[C]//The 2nd Joint Conference On Harmonlous Human Machine Environment(NCMT2006, CHCI2006 and PCC2006).Hangzhou:China Computer Federation,2006:95-101.

[10] Lucas B D,Kanade T.An iterative image registration technique with an application to stereo vision[C]//Proceedings of the 7th International Joint Conference on Artificial Intelligence.Vancouver, BC,Canada:Morgan Kaufmann Publishers Inc.,1981(2):674-679.

[11] Shi J B,Tomasi C.Good features to track[C]//Proceedings of 1994 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Seattle,WA,USA:IEEE,1994:593-600.

[12] Bouguet J Y.Pyramidal implementation of the Lucas Kanade feature tracker description of the algorithm[J].Acta Pathologica Japonica,2000,22(2):363-381.