基于深度学习的短时强降水天气识别

路志英，任一墨，孙晓磊，贾惠珍



基于深度学习的短时强降水天气识别

路志英1，任一墨1，孙晓磊2，贾惠珍3

(1. 天津大学电气自动化与信息工程学院，天津 300072；2. 天津市海洋中心气象台，天津 300074；3. 天津市气象台，天津 300074)

气象预报人员面临的问题之一是如何准确有效地识别短时强降水天气．短时强降水是一种主要由强对流天气形成的气象灾害，产生原因与空气湿度、大气中的水分以及温湿等物理量参数有关，由此提出基于物理量参数和深度学习模型DBNs的短时强降水天气识别模型．首先，利用SMOTE算法人工合成短时强降水少数类(相对于非短时强降水天气类)样本，调整原始数据集不均衡分布问题；然后通过含有高斯玻耳兹曼机的深度学习模型对地面大气监测站逐小时加密的观测量，以及常用于天气预报分析的物理量等低层特征构造出抽象的高层特征，发现数据特征内在关系；最后实现了DBNs短时强降水的自动识别模型．结果表明，该方法能够较为准确地识别短时强降水，对于短时强降水的命中率、误警率和临界成功指数，都有着较好的表现．

短时强降水；物理量计算；SMOTE算法；深度学习

短时强降水是一种突发性强、降水时间短、降水量大的天气过程，主要由强对流天气形成，是一种重要的气象灾害．短时强降水定义为在较短的时间内降水强度较大，其累积降水量数值达到或超过某一量值(通常情况下指1,h累积降水量超过20,mm)的强对流天气．准确地识别短时强降水是气象研究和从业人员的重点研究目标之一．

强降水会带来很多的气象灾害，Jeon[1]使用GIS图像对强降水进行识别，从而发现台风带来的强降水与山坡损坏的关系．Luino[2]通过历史资料研究了强降水给意大利北部带来的一系列危害的过程．目前，国内外很多区域使用雷达回波形成的图像来进行短时强降水的识别，You等[3]使用液滴尺寸分布和偏振雷达对降雨类型进行了分类．单独使用雷达资料或雷达回波图像的强对流天气过程和短时强降水识别也取得了较好的效果[4-6]．然而单独地使用地面观测数据进行强对流天气的识别还存在许多问题，例如气象预报时使用的物理量参数之间的关系不明确，识别精度不高等问题．为了进一步挖掘短时强降水的相关影响因素，本文引入机器学习的方法，在地面观测数据的基础上，构建以深度学习为框架的自动识别 模型．

机器学习在现代社会的各个学科和领域中已经得到了广泛地应用，例如，在计算机视觉、模式识别、数据挖掘、人工智能等领域都取得了很好的效果．深度学习(deep learning，DL)克服了一般机器学习方法中手工选取特征的过程，以及需要非常专业的相关领域的先验知识等缺陷．深度学习通过多隐层的层次结构式神经网络，对容量和维数非常大的数据集进行训练，从中获取相对简单的特征结构，从而构建出鲁棒性非常好的机器学习模型[7]．深度学习通常也被称为深度特征学习，目前，深度学习模型在行人跟踪[8]、风速预测[9-10]等领域有着非常好的效果．

大多数的机器学习方法同等对待数据集中的所有样本，以提升分类器总体分类精度为目标，适用于样本分布比较均匀的数据集[11]．然而，短时强降水是一种在短时间内突发的降水强度大的强对流天气，实际观测和采集到的数据集中，极少数样本为短时强降水天气，而绝大多数样本为非短时强降水天气．若直接应用深度学习模型会造成其在多数样本类的分类精度较高而在少数样本类的分类精度很低的问题．所以，在构建短时强降水深度学习识别模型前，需要通过某种策略调整数据的分布，使数据相对均衡，从而便于识别模型的建立．

本文以地面观测站点所观测的数据为基础，首先根据已有观测到的数据计算相关的温度和湿度等物理量参数；然后利用短时强降水样本人工合成“新”的短时强降水样本；并通过建立深度学习模型，将数据的原始特征组合为高度抽象的特征，从而构建有效的识别模型；最后对模型进行了检验．结果表明，本文提出的方法可以较好地依据地面观测站点所观测的数据实现对短时强降水天气的识别．

1 数据资料

1.1 数据来源

数据来源于中国气象局通过MICAPS业务系统下发的全国自动站逐小时加密的观测数据，其存储形式为AWS格式．

选取2005—2016年每年3—9月间逐小时观测到的海河流域数据作为样本进行分析和处理．选取站点为天津境内国家级别站点，具体分布如图1所示．由于各站点相距足够远，因此，各站点的测试数据可以视为相互独立．

图1 天津境内国家站分布

根据所采用的数据和大气环境系统的实际情况，选取1,h累积降水量大于20,mm的天气情况为短时强降水天气．在选取的469,386条样本数据中有390条短时强降水天气，每条样本数据含有13个观测到的物理量，分别为纬度(°)、经度(°)、地平面气压(hPa)、海平面气压(hPa)、温度(℃)、露点(℃)、相对湿度(%,)、水汽压(hPa)、2,min平均风向(°)、2,min平均风速(m/s)、10,min平均风向(°)、10,min平均风速(m/s)及1,h累积降水量(mm)．

1.2 物理量参数计算

构成天气的基本要素是温、压、湿、风、云等等，正是这些基本要素的变化形成了复杂多变的天气现象．一些基本的物理量参数[12]是天气预报所常用的．根据地面观测站采集到的地面参数，可以计算出如下一些常用的物理量参数．

1) 饱和水汽压

水汽压为大气中由水汽所产生的分压．它的大小由大气中水汽含量的多少决定，单位为hPa．

饱和水汽压的计算经验公式为

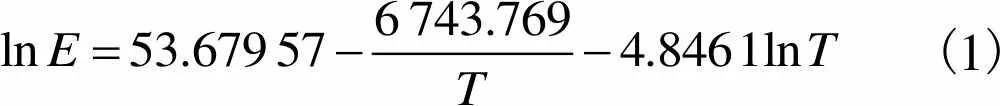
   (1)

式中为绝对温标，K．

式(1)将实际气象业务中可能遇到的情况统一到了一个公式，其计算精度也符合气象业务的需要．

2) 水汽密度

   (2)

式中为水汽压，hPa．

3) 比湿

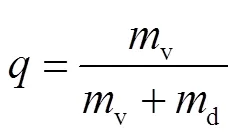
利用状态方程与比湿的定义进行推导，可得比湿的计算公式为

   (3)

式中为大气压力．

比湿具有保守性，对于某一空气团在发生膨胀或压缩时，如果不存在水分的凝结或蒸发，则其水汽质量和空气总质量并不会发生变化，即空气团的体积变化时，它的比湿保持不变．通常用比湿来表示空气的湿度．

4) 温度-露点差

5) 虚温

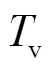
   (4)

在实际情况中，空气的分子量通常随环境水气量的变化而变化，因此湿空气的气体常数是一个变数，定义虚温的用意在于不考虑变动的气体常数，并且便于处理复杂的水汽效应．

6) 位温和虚位温

   (5)

   (6)

7) 整层大气水汽含量

整层大气水汽含量是研究大气辐射和吸收以及全球热量输送的一个重要参量[13-14]，对短时强降水的识别也有着重要的意义．

根据地面参数，可以大致地计算整层大气可降水量，经验公式为

   (7)

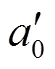
整层大气可降水量还可用地面露点温度表示，具体的经验计算公式为

   (8)

1.3 样本可视化

为了更好地观察地面观测数据与计算出的物理量参数对短时强降水天气的识别结果，本文从中选取相对湿度、温度露点差、2,min平均风速、10,min平均风速及整层大气水汽含量(已标准化，无量纲)，以图像的形式呈现样本分布特点(如图2所示)，其中红色点代表短时强降水天气，绿色代表非短时强降水天气.

从图2的样本分布可知，选取的物理量对于强降水天气和非强降水天气的识别是有一定的作用的，但是存在很多重叠、交叉样本．因此从不同的物理量入手，将其进行有效地组合实现物理量之间的互补与相关，以增加对样本的分类效果．这种提取出真正有用的高维抽象的特征，从而增强对短时强降水天气的识别能力尤为重要．

图2 三维特征样本分布

另外，从图2还可以看出，短时强降水天气相对于非短时强降水天气是一种样本数极少的样本．建立在不均衡数据集上的模型对少数类样本即短时强降水天气的分类精度造成非常大的影响．因此，本文首先使用合成少数类过采样技术(synthetic minority over-sampling technique，SMOTE)算法人工合成“新”的少数类的样本，调整数据集中的样本分布，从而为强降水天气识别模型的建立奠定基础．

1.4 特征维数

为了更加准确地刻画某个时刻短时强降水，本文将某时刻的12个物理量(参见第1.1节)(不包括1,h降水量)以及计算得到的9维相关物理量(参见第1.2节)，与此时刻前1,h、前2,h对应的物理量合并，去除重复的经纬度信息后共计59个物理量作为当前降水量的特征，并以此59维特征构建1,h降水量样本特征数据库，这样通过对样本数据的挖掘，可以更加丰富地刻画和描述与该小时降水量相关信息．

2 SMOTE算法

SMOTE算法的基本思想是：首先对少数类样本进行分析，然后根据少数类样本的特点，人工合成新样本，最后将新样本添加到数据集中从而实现调整不平衡的数据集中样本分布的目的[15]．

SMOTE算法流程描述如下：

(1) 对于少数类中每一个样本，计算它在少数类样本集中以欧式距离为度量的近邻；

(2) 对于每一个少数类样本，从其近邻中随机选择若干个样本；

(4) 将人工合成的新样本添加到原始数据集中，形成新的数据集．

SMOTE算法相对于随机复制样本的算法，可以有效地防止过拟合问题，同时提高分类器的性能．值得注意的是：SMOTE算法中对少数类样本的采样倍率会影响精度的大小，采样倍率越大，对多数类样本的分类精度越低，对少数类样本的分类精度越高．

在利用SMOTE算法得到新数据集的基础上，本文建立了一个基于深度学习模型深度信念网(deep belief networks，DBNs)的短时强降水预报模型．测试结果表明，模型具有性能稳定可有效识别短时强降水天气的能力．

3 深度学习

有监督学习是深度学习应用最广泛的形式，即利用一组已知类别的样本调整深度学习模型参数，使其达到所要求性能的学习．DBNs是一个由限制玻耳兹曼机(restricted Boltzmann machine，RBM)为基本单元所组成的多隐层神经网络模型．其中RBM的训练算法是对比散度(CD-)算法，DBNs是贪心学习算 法[16]．深度学习模型关键是在于其对样本特征提取的能力以及对复杂函数拟合的能力，且比一般的特征提取方法(如主成分分析方法等)有效[17-18]．

与传统的浅层神经网络模型的不同之处在于：深度学习模型首先强调了模型结构的深度；其次明确突出了特征学习的重要性；同时更加具有通过逐层特征变换和组合，将样本在原特征空间的特征表示变换到一个新的特征空间，从而便于分类或预测的特点．在大数据的时代背景下，深度学习在利用大数据更好的学习特征，挖掘数据潜在、丰富的内在信息关系等领域有着很强的优势．

3.1 限制波耳兹曼机

3.1.1 基本概念

DBNs模型的基本组成单元RBM是一种基于能量概念的模型，是玻耳兹曼机(Boltzmann machine，BM)[19]的一种改进．BM是一种来源于统计力学的随机神经网络模型，网络中的神经元是随机神经元，并且神经元的输出只有激活和未激活两种状态．BM拥有强大的无监督学习能力和很强的非线性拟合的能力．RBM在继承了BM强大的无监督学习能力的前提下对其进行了改进，限制了BM显层和隐层的连接[20]．BM和RBM的模型结构如图3所示．

图3 RBM和BM模型结构

相对于BM来说，RBM具有非常好的如下性 质[21-22]：

(1) RBM层内无连接、层间全连接，使得各显元之间的激活条件是独立的，各隐元之间的激活条件也是独立的．这样避免了大量的复杂计算，可以通过Gibbs采样或对比散度(CD-)算法得到随机样本；

(2) 只要隐元的数目足够多，RBM可以拟合任意的离散分布；

(3) 使用CD-算法可以近似模拟Gibbs采样，从而实现快速训练．

因此，相对于BM，可以通过叠加多个RBM来建立深度学习模型，实现提取高度抽象特征，发现数据间隐含存在的关系，避免训练时间过长，便于后续分类模型的建立．

3.1.2 伯努利RBM

假设显元和隐元均为随机二值神经元，即

   (9)

式中：1表示神经元激活状态；0表示神经元抑制状态．这样的RBM为伯努利-伯努利RBM，简称伯努利RBM．其能量函数(energy function)为

   (10)

此时，全概率分布为

   (11)

   (12)

   (13)

   (14)

   (15)

3.1.3 RBM训练算法

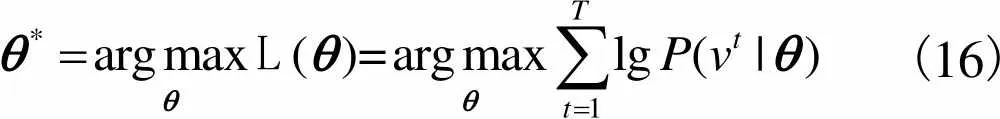
   (16)

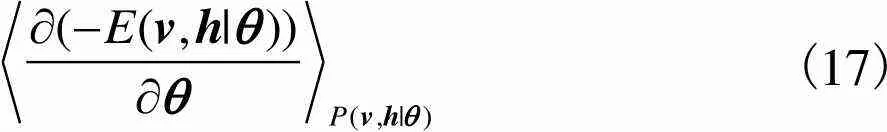
     (17)

图4 CD-算法采样过程

Fig.4 Sampling process of CD-algorithm

   (18)

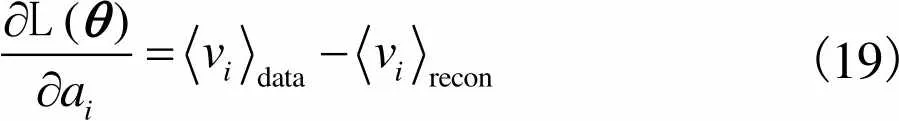
(19)

   (20)

所以RBM的各个参数增量为

   (21)

   (22)

   (23)

根据上述算法求出RBM的每一个参数在数据集中每个训练样本上的增量后，更新各个参数，即可训练好一个RBM．

3.1.4 高斯RBM

应用伯努利RBM的前提是只有当输入数据满足二值分布也就是伯努利分布时，才能取得一个较好的重构，但是实际的数据往往近似于高斯分布而不是伯努利分布，因此需要将伯努利RBM的显元替换为具有独立高斯噪音的线性单元，这样的RBM称为高斯-伯努利RBM，简称高斯RBM．

将式(10)和式(15)改写为

     (24)

   (25)

改写后的高斯RBM和伯努利RBM有着相同的CD-算法，并且CD-算法对于高斯RBM的训练也有较好的效果[24]．

3.2 DBNs训练算法

DBNs是由若干层RBM组成的神经网络模型，其训练过程是：首先通过贪心算法逐层训练RBM，然后叠加训练好的RBM，最后进行微调．DBNs的训练过程包括预训练和参数微调两个过程．

DBNs的预训练过程如下：

(1) 充分训练第1个RBM；

(2) 固定第1个RBM的参数大小，根据其输入向量计算出其隐层状态，将其作为第2个RBM的输入向量；

(3) 充分训练第2个RBM，将训练好的RBM堆叠在第1个RBM的上方；

(4) 重复以上3个步骤若干次．

值得注意的是：如果是无监督学习，那么在训练顶层的RBM时，显层中一起进行训练的神经元，除了显元，还需要有代表分类标签的神经元．

DBNs的微调过程采用了Contrastive Wake-Sleep[25-26]算法对网络参数进行微调，从而达到更好的效果．具体过程如下．

步骤1除了顶层 RBM，令其他层 RBM 的权重分别为向上的认知权重和向下的生成权重．

步骤2Wake 阶段：通过外界的特征输入和认知权重产生每一层的结点状态，并使用梯度下降修改层间生成权重．

步骤3Sleep 阶段：通过顶层表示和生成权重，生成底层状态，同时修改层间的认知权重．对于有监督的识别任务，DBNs的训练过程如图5所示．

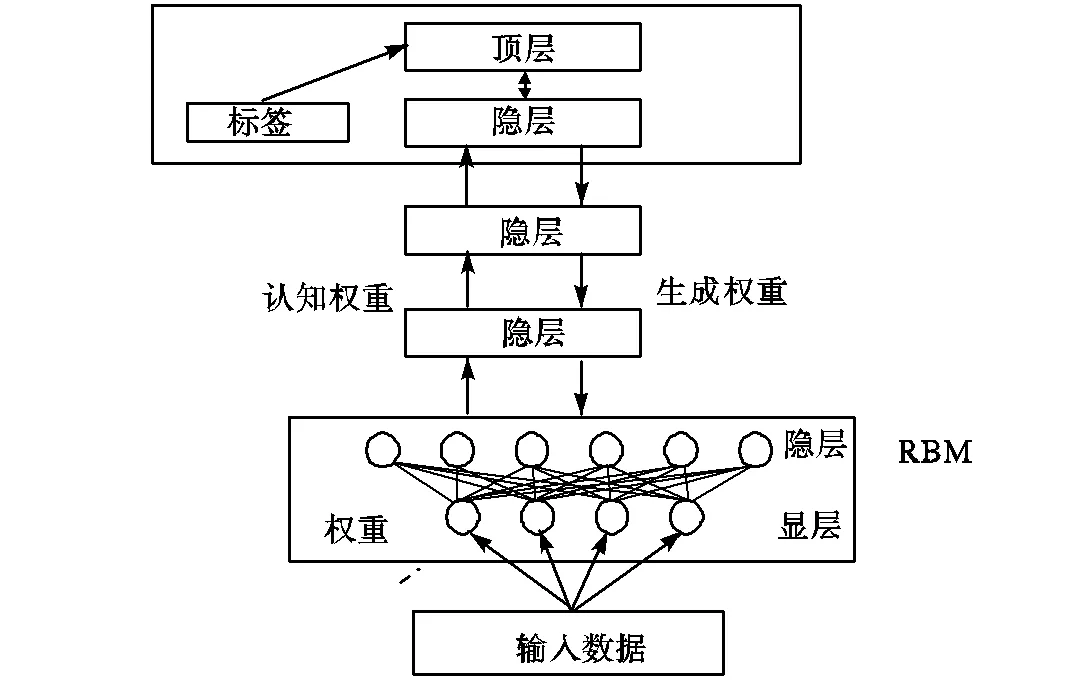
图5 DBNs训练过程

4 建立短时强降水识别

4.1 数据集的选取

将构建好的数据集分为两部分和，和分别占原始数据集的75%,和25%,．

首先利用SMOTE算法扩充数据集的正例(短时强降水)样本为数据集，缓解数据集的不平衡；然后将数据集归一化为数据集并将数据集切分成3个部分，分别为训练集、验证集和测试集，各约占数据集的50%,、25%,、25%,．训练集用于训练模型，验证集用于对模型的微调，测试集用于对模型结果的检验．

最后，通过数据集对模型进行测试．值得注意的是，数据集中的数据既包括短时强降雨天气样例，又包括非短时强降雨天气样例，均是没有参与模型训练过程的真实数据．

4.2 DBNs短时强降水识别模型建立

本文构造了一个具有3个RBM以及顶层为LR回归的DBNs短时强降水识别模型，其中，DBNs的第1个RBM为高斯RBM，作为输入层，其节点数为59，分别是地面观测站数据及物理量参数计算结果；输出层节点数是2，为强降水识别结果(是或者不是)；隐层节点数为100．DBNs模型结构如图6所示.

DBNs模型的建立过程如图7所示．

4.3 评价指标

为了对基于DBNs强降水识别模型的识别结果进行统计和分析，引入多个指标进行评价[27]．

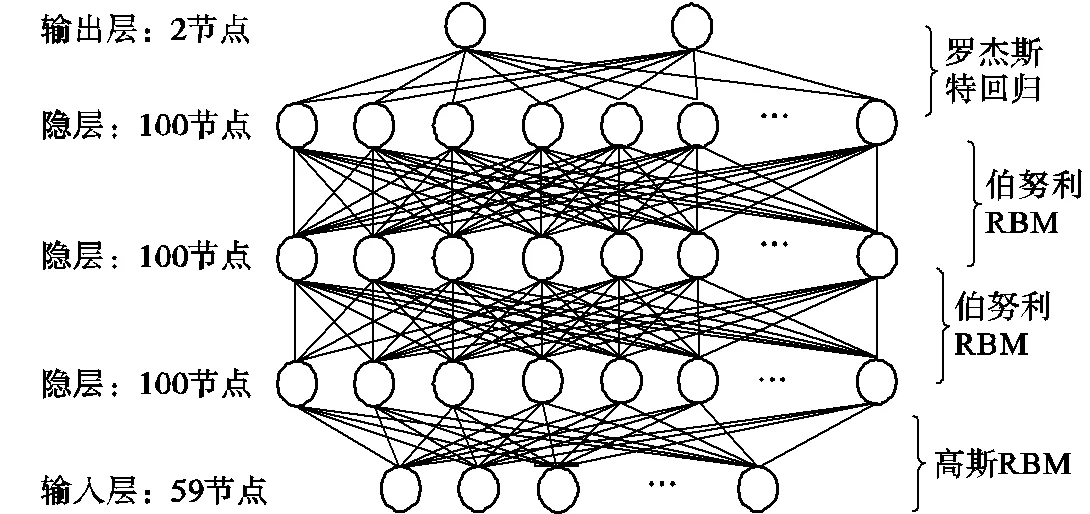
图6 DBNs模型结构

图7 DBNs训练流程

在气象领域中，命中率(percent of doom，POD)、误警率(false alarm rate，FAR)和临界成功指数(critical success index，CSI)可以准确评价对短时强降水的识别和预报效果．

以强降水为例，POD、FAR和CSI分别定义为

      (26)

      (27)       (28)

4.4 识别结果与分析

为了说明本文DBNs短时强降水识别模型的性能，将第4.1节数据集作为训练样本，分别构建基于LR和SVM短时强降水天气识别模型，并用数据集对模型进行测试．DBNs、LR和SVM模型的识别结果如表1所示．

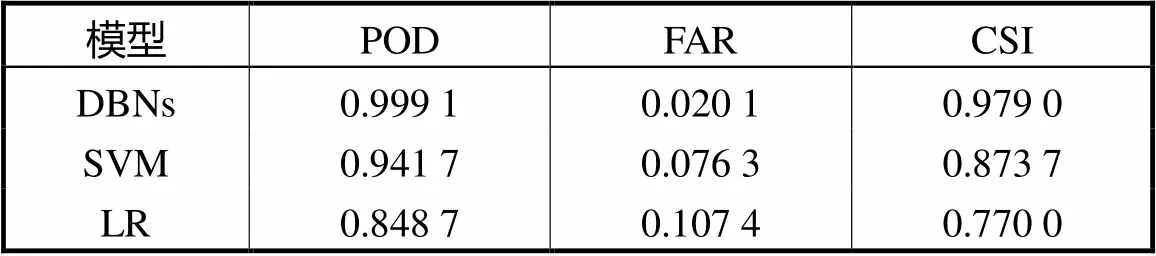
表1 识别结果

由识别结果可知，3种机器学习模型输出识别结果的评价指标均能够取得较好的识别效果，说明通过机器学习的方法，在地面观测数据及物理量参数计算的基础上，能够准确有效地识别短时强降水天气，但DBNs模型的各项指标均优于SVM及LR模型的各项指标，这说明本文DBNs模型以地面观测数据为基础上的短时强降水识别能力最强，性能更加优越．

实验结果所得DBNs短时强降水识别模型的各项指标均大大地优于LR模型的各项指标，充分说明由于RBM“特征学习”和“特征选择”的作用，DBNs在对处理天气观测数据这种大而全的“大数据”时，可以在其丰富的数据中，更加有效地提取出有用的信息，将输入的物理量叠加组合成更高级更抽象的特征物理量，从而提高了模型识别的能力．

4.5 预报结果与分析

为了说明本文建立的DBNs在短时强降雨天气预报方面所发挥的作用，将数据的降水量标签提前1,h，即将包括当前时刻在内的前3,h地面观测数据与计算的相关物理量作为特征，未来1,h天气状况为标签进行模型训练，可获得1,h提前预报模型，从而使其更具有实际应用的意义．表2为采用DBNs、LR和SVM模型对短时强降水天气1,h提前预报结果．

表2 1,h提前预报结果

Tab.2 Results of prediction forcasting in 1,h

由1,h提前预报结果可知，DBNs模型的各项指标依然均优于SVM及LR模型的各项指标．

DBNs模型作为一种人工智能的技术，在大数据的时代背景下，能够满足实际的气象工作人员对短时强降雨天气的1,h提前预报的需求．

5 结 论

本文选取天津市2005—2016年每年3—9月间逐小时观测到的469,386数据，其中有390条数据为短时强降水天气，在地面观测数据及部分计算物理量的基础上，提出了基于物理量参数和深度学习模型的DBNs短时强降水天气识别预报模型，根据模型检验的结果，可以得出以下结论．

(1) 以地面观测站逐小时观测到的基本天气数据为基础进行部分温湿度物理量的计算，并对其进行了分析和处理，从而构建出基于物理量参数的DBNs短时强降水天气识别模型，有效地识别了短时强降水.

(2) 利用SMOTE算法在不均衡的数据集中人工合成少数类样本(短时强降水)，有效地保证了本文识别模型的识别能力，使DBNs短时强降水模型能准确地识别出短时强降水．

(3) 叠加的RBM可以提取出高度抽象的特征，从而大大地提高了识别模型的识别能力，使得DBNs在已有的数据集上可以取得比RBM和LR模型更好的效果．

(4) 本文通过对现有数据集的处理，用DBNs模型实现了对短时强降雨天气的1,h提前预报，实验结果表示DBNs模型作为一种天气预报模型，能够取得较好的提前预报的效果．

［1］ Jeon S S. Damage pattern recognition of spatially distributed slope damages and rainfall using optimal GIS mesh dimensions[J].，2014，11(2)：336-344.

［2］ Luino F. Sequence of instability processes triggered by heavy rainfall in the Northern Italy[J].，2005，66(1/2/3/4)：13-39.

［3］ You C H，Lee D I，Kang M Y，et al. Classification of rain types using drop size distributions and polarimetric radar：Case study of a 2014 flooding event in Korea[J].，2016，181：211-219.

［4］ Root B，Yu T Y，Yeary M. Consistent clustering of radar reflectivities using strong point analysis：A prelude to storm tracking[J].，2011，8：273-277.

［5］ 胡文东，杨 侃，黄小玉，等. 一次阵风锋触发强对流过程雷达资料特征分析[J]. 高原气象，2015，34(5)：1452-1464.

Hu Wendong，Yang Kan，Huang Xiaoyu，et al. Analysis on a severe convection triggered by gust front in Yinchuan with radar data[J].，2015，34(5)：1452-1464(in Chinese).

［6］ 张家国，王 珏，黄治勇，等. 几类区域性暴雨雷达回波模型[J]. 气象，2011，37(3)：285-290.

Zhang Jiaguo，Wang Jue，Huang Zhiyong，et al. Several kinds of region rainstorm radar echo models[J].，2011，37(3)：285-290(in Chinese).

［7］ Arel I，Rose D C，Karnowski T P. Deep machine learning—A new frontier in artificial intelligence research [research frontier][J].，2010，5(4)：13-18.

［8］ Kalal Z，Mikolajczyk K，Matas J. Tracking-learning-detection[J].，2012，34(7)：1409-1422.

［9］ Wan J，Liu J，Ren G，et al. Day-ahead prediction of wind speed with deep feature learning[J].，2016，30(5)：433-438.

［10］ Zhang C Y，Chen C L P，Gan M，et al. Predictive deep Boltzmann machine for multipored wind speed forecasting[J].，2015，6(4)：1416-1425.

［11］ 尹 剑，陆程敏，杨贵军. 判别分析与Logistic回归组合分类[J]. 数理统计与管理，2014，33(2)：256-265.

Yin Jian，Lu Chengmin，Yang Guijun. Combinations of discriminatory analysis and logistic regression for classification[J].，2014，33(2)：256-265(in Chinese).

［12］ 刘健文. 天气分析预报物理量计算基础[M]. 北京：气象出版社，2005.

Liu Jianwen.[M]. Beijing：China Meteorological Press，2005(in Chinese).

［13］ 杨景梅，邱金桓. 用地面湿度参量计算我国整层大气可降水量及有效水汽含量方法的研究[J]. 大气科学，2002，26(1)：9-22.

Yang Jingmei，Qiu Jinhuan. A method for estimating perceptible water and water vapor content from ground humidity parameters[J].，2002，26(1)：9-22(in Chinese).

［14］ 李 超，魏合理，刘厚通，等. 合肥整层大气可降水量与地面露点相关性分析[J]. 高原气象，2009，28(2)：452-457.

Li Chao，Wei Heli，Liu Houtong，et al. Correlation analyses on total perceptible water and surface dew point temperature over Hefei[J].，2009，28(2)：452-457(in Chinese).

［15］ Chawla N V，Bowyer K W，Hall L O，et al. SMOTE：Synthetic minority over-sampling technique [J].，2002，16(1)：321-357.

［16］ Hinton G，Osindero S，Teh Y. A fast learning algorithm for deep belief nets[J].，1989，18(7)：1527-1554.

［17］ Hinton G E，Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J].，2006，313(5786)：504.

［18］ Chabiron O，Malgouyres F，Tourneret J Y，et al. Toward fast transform learning[J].，2015，114(2/3)：195-216.

［19］ Pelillo M，Refice M. Learning compatibility coefficients for relaxation labeling processes[J].，1994，16(9)：933-945.

［20］ Najafabadi M M，Villanustre F，Khoshgoftaar T M，et al. Deep learning applications and challenges in big data analytics[J].，2015，2(1)：1-10.

［21］ Roux N L，Bengio Y. Representational power of restricted Boltzmann machines and deep belief networks [J].，2008，20(6)：1631-1632.

［22］ Hinton G E. A practical guide to training restricted Boltzmann machines[J].，2012，9(1)：599-619.

［23］ Yamashita T，Tanaka M，Yoshida E，et al. To be Bernoulli or to be Gaussian，for a restricted Boltzmann machine[C]//，. Sweden，2014：1520-1525.

［24］ Hinton G E. Training products of experts by minimizing contrastive divergence[J].，2002，14(8)：1771-1800.

［25］ Karakida R，Okada M，Amari S I. Dynamical analysis of contrastive divergence learning：Restricted Boltzmann machines with Gaussian visible units[J].，2016，79(C)：78-87.

［26］ Hinton G E，Dayan P，Frey B J，et al. The "wake-sleep" algorithm for unsupervised neural networks[J].，1995，268(268)：1158-1161.

［27］ 路志英，刘 海，贾惠珍，等. 基于雷达反射率图像特征的冰雹暴雨识别[J]. 物理学报，2014，63(18)：485-496.

Lu Zhiying，Liu Hai，Jia Huizhen，et al. Recognition of hail and rainstorm based on the radar reflectivity image features[J].，2014，63(18)：485-496(in Chinese).

(责任编辑：孙立华)

Recognition of Short-Time Heavy Rainfall Based on Deep Learning

Lu Zhiying1，Ren Yimo1，Sun Xiaolei2，Jia Huizhen3

(1．School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China；2．Tianjin Marine Meteorological Center，Tianjin 300074，China；3. Tianjin Meteorological Bureau，Tianjin 300074，China)

One of the key studies for meteorological practitioners is how to recognize and predict short-time heavy rainfall accurately and effectively．The short-time heavy rainfall is a severe meteorological disaster that is mainly caused by strong convective weather，which is related to such physical parameters as air humidity，moisture in the atmosphere，temperature and humidity．In this paper，a recognition model of the short-time heavy rainfall based on physical parameters and deep learning model DBNs is constructed．Firstly，SMOTE algorithm is used to synthesize a few samples of the short-time heavy rainfall，which is much less than normal weather，to adjust the distribution of the original data set．Secondly，a deep learning model with a Gaussian Boltzmann machine is constructed based on the observed data from automatic monitoring stations on a local ground and the physical quantities commonly used in weather forecast analysis．Finally，the automatic recognition model of short-term heavy rainfall is obtained．Through the analysis of the experimental results，the model can accurately recognize the short-time heavy rainfall，and have a good performance in the POD，FAR and CSI of short-time heavy rainfall recognition.

short-time heavy rainfall；physical quantity；SMOTE algorithm；deep learning

10.11784/tdxbz201703106

TP29

A

0493-2137(2018)02-0111-09

2017-03-31；

2017-08-22.

路志英（1964—  ），女，博士，教授.

路志英，luzy@tju.edu.cn.

国家自然科学基金资助项目(41575049)；天津市自然科学基金青年项目(16JQNJC07500).

the National Natural Science Foundation of China(No.,41575049)and the Youth Project of Natural Science Foundation of Tianjin，China(No.,16JQNJC07500).