一种静态单点定位的事后精密星历组合滤波方法

陈佳清，刘立龙，黎峻宇，刘瑞驹，刘家智

(1.钦州市住房和城乡建设测绘院，广西 钦州 535000；2.桂林理工大学 测绘地理信息学院，桂林 541006；3.广西空间信息与测绘重点实验室，桂林 541006)

0 引言

全球卫星导航系统(global navigation satellite system，GNSS)已经在各行各业中得到了广泛的应用，国际GNSS服务组织(International GNSS Service，IGS)也对各类产品解算不断进行改进和优化，精密单点定位技术(precise point positioning，PPP)研究进入了一个新阶段[1]。国内外科研院校、生产部门的学者相继对精密单点定位技术进行了大量理论研究和技术创新[2-8]，精密单点定位数据处理软件开发技术越来越成熟。国外有加拿大Waypoint公司推出的GrafNav软件、APPLA-Ni X公司的POSPac AIR、挪威Terra Tec公司的Terra POS软件、瑞士Leica公司的IPAS等，但是这些都是商用软件，价格较为昂贵、不提供源代码，且数据处理过程较为繁杂。国内有武汉大学研发的精密单点定位软件TriP，其源代码不公开[1]。

RTKLIB是日本东京海洋大学(Tokyo University of Marine Science and Technology)开发的一个用于GNSS精确定位的开源软件[9]，与其他商用软件相比，其最大的优势在于免费，且所有源代码公开，便于学习研究和算法测试[10]。为此，国内外学者陆续对其性能进行了大量的相关试验及应用研究。国外关于RTKLIB的研究起步较早，并已成功应用在相关领域：文献[11]中利用低成本的全球定位系统(global positioning system，GPS)模块u-blox和天线，借助RTKLIB软件处理获得了厘米级的静态定位；文献[12]评估了RTKLIB的准确性，成功达到了安装在飞机上的合成孔径雷达(SAR)厘米级的精度要求；文献[13]利用RTKLIB软件处理GNSS数据测定冰川坐标及流速。国内方面：文献[10]研究利用RTKLIB软件精密单点定位精度达厘米级；文献[14]利用RTKLIB软件分析了不同星历、钟差对定位精度的影响，得出事后星历和快速星历单天解3维坐标分量得收敛值方向偏差在4 cm左右的结论；文献[15]对比了BERNESE5.2和RTKLIB软件静态单点定位解算精度。已有的文献在研究RTKLIB静态精密单点定位过程中，均采用前向滤波方法进行数据处理，而RTKLIB软件提供了多种解算方式[16]，因此对其应用研究尚不够完善和全面。

本文对比分析RTKLIB在不同星历产品、不同滤波方法和不同观测时间下的解算精度，探求采用精密星历结合组合滤波方法的更优解算策略。

1 RTKLIB静态单点定位关键技术

1.1 GPS精密单点定位数学模型

GPS单点定位采用载波相位与伪距无电离层组合[10](Ionosphere-free LC)观测方程[5]，观测方程简化为：

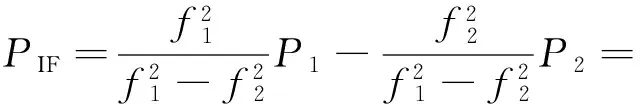
(1)

(2)

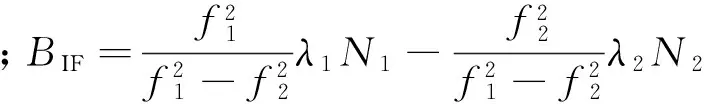
1.2 基于EKF的数据处理

RTKLIB软件精密单点定位中采用的数据处理算法为扩展卡尔曼滤波(extended Kalman filter，EKF)[16]。运用卡尔曼滤波算法，通过tk时刻系统观测向量yk的更新估算未知参数状态向量x及其协方差矩阵P，其滤波方程为：

(3)

(4)

(5)

(6)

RTKLIB在静态精密单点定位中采用EKF对GNSS测量信号、对流层、电离层等进行滤波处理。对于事后PPP，其滤波类型有前向、后向、组合3种方法[16]。

2 数据预处理及误差改正

从RTKLIB源代码可以看到，在RTKLIB预处理模块中采用的是电离残差(L1-L2 geometry free)周跳探测法，该方法只对周跳进行探测不进行周跳修复[10]。为获得精密单点解算最优精度进行的误差改正有：1)电离层时延改正，为了消除GNSS信号测量中的电离层效应，采用无电离层组合模型进行GNSS数据处理；2)对流层时延改正，采用精密对流层模型“Estimate ZTD”估计天顶总对流层延迟改正；3)星历、钟差改正采用国际IGS中心提供的事后精密星历、钟差文件进行改正。

3 实验及结果分析

算例采用BJFS、CHAN、SHAO 3个IGS站1 877 GPS星期第5天的数据，采样间隔为30 s。数据处理之前首先下载该天3个IGS站的观测文件和导航文件(BJFS18770010.16o、BJFS18770010.16n，CHAN18770010.16o、CHAN18770010.16n，SHAO18770010.16o、SHAO18770010.16n)，并从ftp：//garner.ucsd.edu/网站下载实验所需sp3格式的IGS精密星历数据：igs18775.sp3、igr18775.sp3、igu18775.sp3以及精密钟差文件igs18775.clk。

3.1 基于RTKLIB的数据质量分析

在静态单点定位解算之前利用RTKLIB软件对数据质量进行分析，必要的预处理是提高解算精度的前提。绘制3个IGS站卫星分布图(如图1所示)，高度角、多路径误差、信噪比如图2所示。

从图1可以看出：3个IGS站的卫星分布状态良好，BJFS站卫星可视化程度较另外2站稍差，初步推断可能受建筑物或其他物体遮挡。从图2可以看出：3个IGS站的卫星高度角基本保持一致；多路径误差随观测时间的增加而变小，BJFS站的多路径误差均方根(root mean square，RMS)值为0.394 7 m，CHAN站的多路径误差RMS值为0.600 7 m，SHAO站的多路径误差RMS值为0.475 7 m，多路径误差最大为CHAN站；信噪比随观测时间的增加而增强，CHAN、SHAO 2个IGS站的信噪比SNR在40 至60 dB之间。

根据上述IGS各站观测数据质量分析结果初步得出SHAO站观测质量最优。

3.2 精密单点定位精度分析

经RTKLIB质量分析后，分别对3个IGS站进行静态单点定位解算。解算过程中统一采用精密钟差产品，对比不同星历产品、不同滤波方式、不同观测时间下的解算精度并进行统计分析。IGS各站点东向(E)、北向(N)、天向(U)收敛偏差值统计如表1所示。

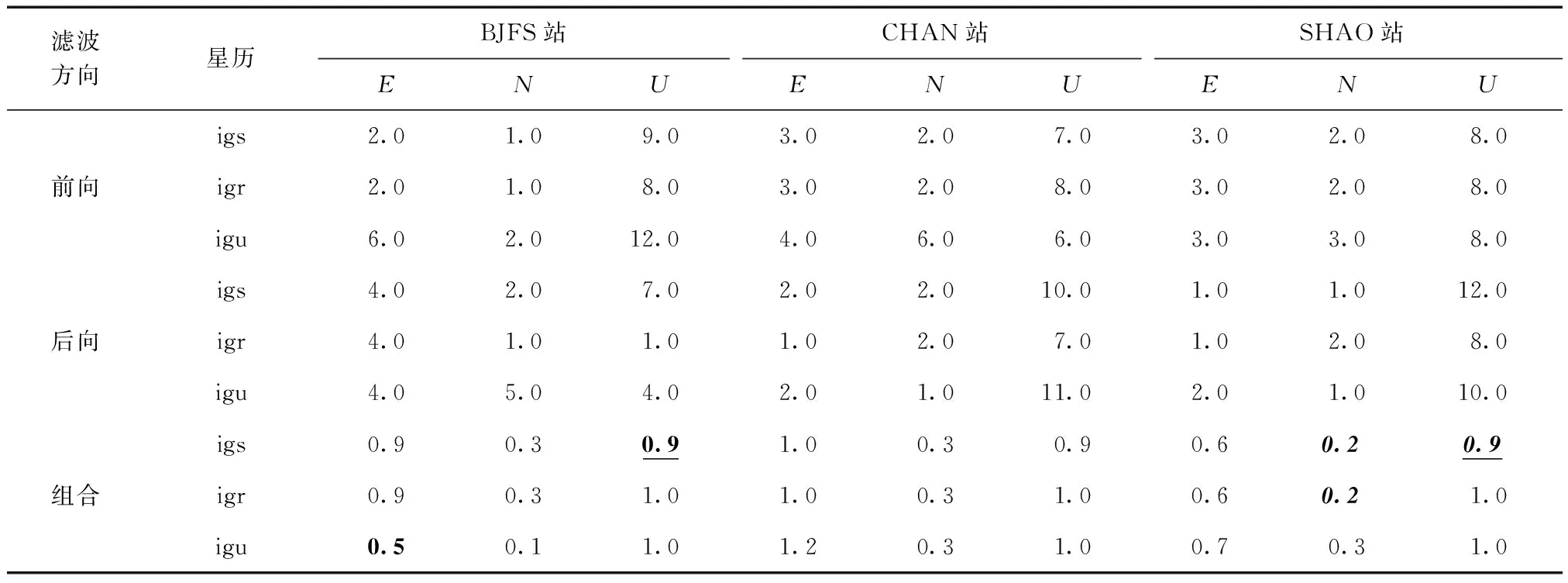
表1 IGS各站点E、N、U方向收敛偏差值 cm

注：前向、后向收敛值为最终收敛值，组合收敛值为单天区间内收敛值；字体加粗表示E方向最小值，字体加粗加斜表示N方向最小值，字体加粗加下划线表示U方向最小值。

从表1中可以看出：1)采用igs和igr星历解算单天IGS各站点E、N、U方向收敛值基本一致，优于igu星历，N方向收敛偏差值小于E、U方向；2)采用组合滤波方法优于前向和后向滤波方法，BJFS、CHAN、SHAO 3个IGS站的3个方向收敛偏差值均不大于1 cm；3)采用igs星历结合组合滤波方法后，收敛偏差最小值E方向为0.5 cm、N方向为0.2 cm、U方向为0.9 cm；4)SHAO站收敛偏差结果优于另外2个IGS站。IGS各站点E、N、U方向及RMS值统计如表2所示。

表2 IGS各站点E、N、U方向及平面RMS值 cm

注：字体加粗表示E方向RMS最小值，字体加粗加斜表示N方向RMS最小值，字体加粗加下划线表示U方向RMS最小值，字体加粗加双下划线表示平面点位中误差最小值。

从表2中可以看出：1)采用igs星历组合滤波方法，IGS各站点E、N、U方向RMS值及平面中误差均小于0.6 cm，RMS最小值N方向为0.06 cm、E方向为0.1 cm、U方向为0.29 cm，点位中误差最小值为0.29 cm；2)3个IGS站解算结果均获得毫米级精度，解算最优结果的IGS站点为SHAO站，点位精度为0.29 cm；3)解算结果表明RTKLIB静态单点定精度达到毫米级。IGS各站的收敛偏差值(事后精密星历结合组合滤波法)如图3～图5所示。

由图3可知：BJFS站的E方向偏差收敛不稳定，U方向稳定性较E方向差，N方向整体平稳，无明显波动；E、U方向波动幅度在0.9 cm内，N方向波动幅度在0.3 cm内；E、N、U方向RMS值分别为0.47、0.09及0.33 cm。

由图4可知：CHAN站的E方向偏差收敛不稳定，U方向稳定性较E方向差，N方向整体平稳，无明显波动；E、U方向波动幅度在1 cm内，N方向波动幅度在0.3 cm内；E、N、U方向RMS值分别为0.54、0.11及0.33 cm。

由图5可知：SHAO站的E方向偏差收敛不稳定，U方向稳定性较E方向差，N方向整体平稳，无明显波动；E、U方向波动幅度在0.9 cm内，N方向波动幅度在0.2 cm内；E、N、U方向RMS值分别为0.29、0.06及0.29 cm。

对比图3～图5可知：BJFS、CHAN、SHAO 3个IGS站的E、N、U方向收敛值偏差基本一致，E方向收敛偏差值不稳定，但最大偏差值不超过1 cm；N方向收敛偏差值较为平稳，在0.4 cm以内；U方向收敛偏差值波动较大，但也不超过1 cm。以SHAO站为例，不同观测时间对解算精度的影响如图6所示。

由图6可知：E、N、U方向精度曲线基本一致，精度随着观测时间的递增而提高；N、U方向在观测24 h时精度最高，RMS最小值分别为0.06和0.29 cm，略优于文献[2]中的0.1和0.3 cm；E方向在观测时段14时至20时由于受到观测粗差的影响，精度随时间递增而减小；受到E方向精度的影响，平面精度出现同样的影响；E方向及平面在观测14 h时精度最高，RMS最小值分别为0.19和0.23 cm；观测4 h左右时的平面精度达厘米级，在观测条件良好条件下，单天解算精度可达毫米级。

综合上述静态单点定位精度分析结果，对于高精度单点定位解算可参考以下静态精密单点定位更优解算策略，如表3所示。

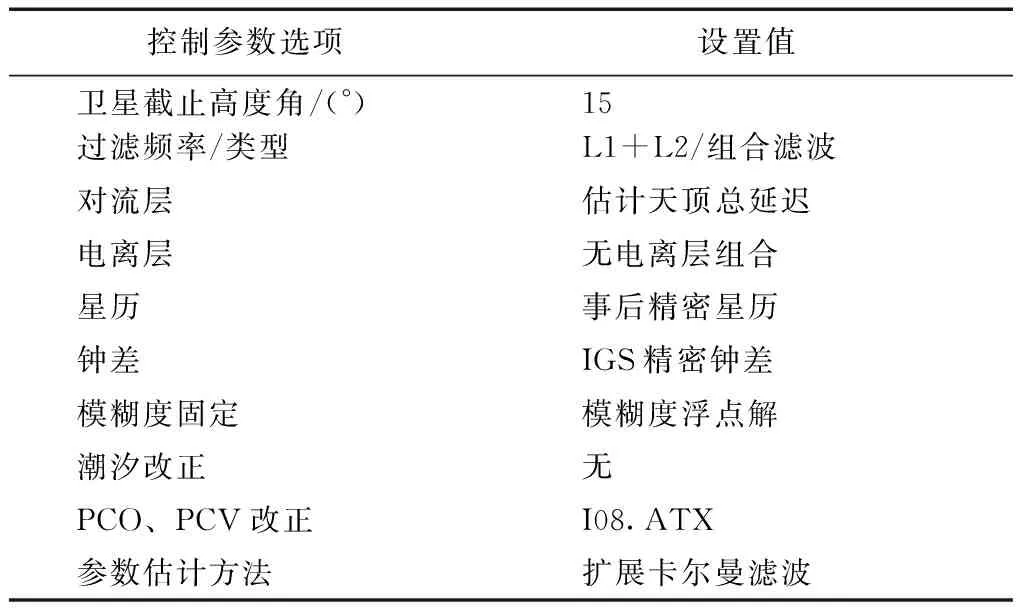
表3 静态精密单点定位更优解算策略

注：PCO全称为phase center offset，指接收机天线相位中心改正；PCV全称为phase center variation，指相位中心偏差；I08.ATX为改正文件。

4 结束语

RTKLIB软件静态精密单点定位解算结果表明：igs星历和igr星历解算精度相当，优于igu星历；前向滤波和后向滤波方法解算精度略有所差异但并不明显，组合滤波方法相对于其他2种方法能够提高10倍以上精度；解算精度随观测时间的增加而提高，同时受到观测过程中误差的影响而出现突变。采用事后精密星历结合组合滤波方法，3个IGS站单天解E、N、U3个方向偏差收敛值均在1 cm内，E、N、U方向及平面定位精度达到毫米级。其中，SHAO站的静态精密定位精度为0.29 cm，优于其他2站，验证了RTKLIB数据质量分析中SHAO站观测质量最优的结论。在静态精密单点定位中，RTKLIB具有解算精度高、效率高、可靠性高的特点，对目前的地壳形变监测及工程应用具有重要的现实意义。

[1] 张小红，何锡扬，李星星.TriP软件非差几何法精密定轨精度分析[J].武汉大学学报(信息科学版)，2010，35(11)：1327-1330.

[2] 张小红，左翔，李盼，等.BDS/GPS精密单点定位收敛时间与定位精度的比较[J].测绘学报，2015，44(3)：250-256.

[3] 赖允斌，赵春梅，李子申.不同星历下实时精密单点定位精度分析[J].测绘通报，2015(8)：9-12.

[4] 周磊.GNSS精密单点定位理论及其软件研制[D].西安：西安科技大学，2015.

[5] 臧楠.BDS/GNSS精密单点定位算法研究[D].西安：长安大学，2015.

[6] OLIVEIRA P S，MOREL L，FUND F，et al.Modeling tropospheric wet delays with dense and sparse network configurations for PPP-RTK[J].GPS Solutions，2017，21(1)：237-250.

[7] GANDOLFI S，TAVASCI L，POLUZZI L.Study on GPS-PPP precision for short observation sessions[J].GPS Solutions，2016：1-10.

[8] EL-MOWAFY A，DEO M，RIZOS C.On biases in precise point positioning with multi-constellation and multi-frequency GNSS data[EB/OL].(2016-12-09)[2017-02-18].https：//www.researchgate.net/profile/Ahmed_El-Mowafy/publication/291384900_On_biases_in_precise_point_positioning_with_multi-constellation_and_multi-frequency_GNSS_data/links/5705d3c208ae13eb88b97d16.pdf?origin=publication_detail.

[9] Tokyo University of Marine Science and Technology Laboratory of Communications Engineering.RTKLIB：An open source program package for GNSS positioning[EB/OL].(2016-12-19)[2017-02-18].http：//www.rtklib.com/rtklib.htm.

[10] 丁慧君，罗端，卢兵.基于RTKLIB的精密单点定位研究[J].城市勘测，2014，10(5)：22-25.

[11] WISNIEWSKI B，BRUNIECKI K，MOSZYNSKI M.Evaluation of RTKLIB’s positioning accuracy using low-cost GNSS receiver and ASG-EUPOS[J].Transnav International Journal on Marine Navigation & Safety of Sea Transportation，2013，7(2)：79-85.

[12] VIDEKULL R.Evaluate and develop high-performance GPS navigation using free GPS software[D].Göteborg，Sweden：Chalmers University of Technology，2015.

[13] SUGIYAMA S，SAKAKIBARA D，TSUTAKI S，et al.Glacier dynamics near the calving front of Bowdoin Glacier，northwestern Greenland[J].Journal of Glaciology，2015，61(226)：223-232.

[14] 张建龙，徐爱功，张兆南，等.RTKLIB软件静态精密单点定位精度测试与分析[J].全球定位系统，2014，39(1)：37-41.

[15] 汪洋.GNSS精密单点定位数据解算结果的比较和分析[C]//中国卫星导航系统管理办公室学术交流中心.第七届中国卫星导航学术年会论文集.北京：中国卫星导航系统管理办公室，2016：1-4.

[16] TAKASU 1 T，YASUDA A.RTKLIB ver.2.4.2 manual[EB/OL].(2013-04-29)[2017-02-18].http：//www.rtklib.com/prog/manual_2.4.2.pdf.