电离层TEC预报模型的卡尔曼滤波改进方法

王建敏，黄佳鹏，祝会忠，马天明

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

0 引言

由于电离层自身的不稳定性，对于穿过该层的全球卫星导航系统(global navigation satellite system，GNSS)的电波会产生折射、散射等物理现象。正常情况下电离层的反射有助于GNSS无线电信号传播，但是E层和F层剧烈变化对GNSS信号会产生严重的影响。电离层总电子数(total electron content，TEC)是电离层的重要特性之一，测量电离层中的总电子含量、研究其变化规律并对其进行预报是一项重大的研究课题。因此研究预报模型，对电离层TEC的变化情况进行高精度预报，进而揭示电离层的物理机制，具有重要的科研及实用意义[1-8]；文献[2]使用国际全球卫星导航系统服务组织(International GNSS Service，IGS)公布的电离层TEC进行自回归滑动平均模型(auto regressive and moving average model，ARMA)的建模与预测，以电离层平静期和活跃期为研究对象，预报6 d相对精度达80 %以上；文献[3]使用ARMA模型对电离层TEC进行预报，以24 h为预报时间，精度可达90 %；文献[4]利用夹角余弦和聚类分析对电离层TEC进行混沌预测，得到的预测值在标准差和均方根(root mean square，RMS)2个指标方面得到较好结果；文献[5]利用神经网络模型完成1 d的电离层TEC预报，表明训练好的神经网络模型能够充分反映出不同季节电离层TEC的变化；文献[6]通过分析TEC的各个趋势项，确定模型相应参数，完成时间序列模型的预测；文献[7]将奇异谱分析方法(singular spectrum analysis，SSA)与ARMA模型结合，使用SSA方法分解TEC数据，再利用ARMA模型完成电离层TEC预报，结果表明组合模型的预报精度相对仅利用ARMA模型预报提高了4 %；文献[8]利用自回归模型(auto regressive model，AR)模型与误差反向传播(back propagation，BP)神经网络模型等组合模型完成电离层TEC预报，得出组合模型相对单一模型完成预报可得到更好的预报结果的结论。目前所有研究均是直接基于IGS公布的数据完成预报，对于预处理方式大多以差分方式使数据平稳化；但差分方式多是以简单数学模型完成，并不完全遵循数据的变化规律，只能完成数据平稳化处理。

卡尔曼滤波是以最小无偏差性为准则的数据处理模型。本文将卡尔曼滤波引入电离层TEC预报的预处理，以滤波算法对IGS网站公布的电离层原始数据进行降噪处理，减小噪声对于组合模型建立和预报的影响，再使用AR模型和BP神经网络模型的组合模型进行预测，分析比较滤波前后数据预测精度及模型适用条件。

1 模型基本原理

1.1 卡尔曼滤波

卡尔曼滤波是一种利用线性系统状态方程对系统状态进行最优估计的算法，它能减少随机噪声对电离层TEC观测量的影响。它具有最小无偏差性，是当前应用最广的一种数据预处理方法。它处理数据不仅会去除突变的数据，而且会保持数据原有的变化趋势，这样有利于预报模型的建立。离散线性系统的卡尔曼滤波方程包括状态方程和观测方程[9]，即：

(1)

L(k)=B(k)X(k)+Δ(k)。

(2)

通过最小二乘原理可推得卡尔曼滤波方程为：

(3)

(4)

Dx(k)=(E-J(k)×B(k))×Dx(k-1)]。

(5)

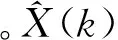
1.2 AR模型

AR模型全称为自回归模型，是使用过去时间段的数据建立模型获得权值，利用权值及过去时间段的数据进行加权生成预测值。因此通过建立AR模型，可以对电离层TEC数据进行预测。AR模型是使用一段随时间变化而变化的数据序列，用相应的模型加以描述，基于原始观测量可以充分反映相关因素对预测数据的影响和作用，不受模型各个变量相互独立的假设条件约束，所生成的描述模型可以消除一般预测方法中由于参数不明确、自变量选择等造成的困难。数学模型的建立更多基于原始数据，更能发现这些数据本质的、内在的规律。

自回归AR模型为

(6)

(7)

式中：

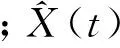
1.3 BP神经网络模型

BP神经网络是神经网络中被广泛使用的一种模型。BP神经网络的特点是在运算过程中可以进行学习修正功能，包括自我学习、训练以及泛化等功能，可以实现对于数据反复运算，不断修正相应参数和权值，直至达到预期数值。BP神经网络是一种多层反复运算神经网络结构。如图1所示，BP神经网络最基本的拓扑结构是3层，包括输入层、输出层和一个隐层，上一层各个神经元与下一层所有的神经元连接，但是同一层各个神经元之间没有联系，导致数据在运算过程中，每层的神经元只会影响到下一层的权值，对其他层没有影响。若运算过程并没有得到理想的数值输出，会计算误差的值，随后进行学习过程，这一过程是反向传播的，通过不断学习训练误差值，调节参数和权值，直到输出值小于期望值，则输出运算结果值[13-18]。以电离层TEC滤波值作为BP神经网络的输入值完成训练、建模和预报。

1.4 组合模型

由于AR模型和BP神经网络模型在完成电离层TEC预测时都留有残差，为减少误差较大的模型对组合模型的影响，组合过程中选择改进的加权组合方式，其表达式为

C(n)=αA(n)+βB(n)。

(8)

式中；A(n)为AR模型对电离层TEC的预测值；B(n)为BP神经网络模型对TEC的预测值；C(n)为组合模型的预测值，其中n表示组合模型的第n项；α与β分别为组合模型中2个单一模型的权值。为充分利用2个模型预测值，减少模型在组合过程中的运算量，需要限制α与β的取值，即当AR模型残差优于BP神经网络模型，取AR模型权值α为1，BP神经网络模型权值β为0，以此方式减少误差较大模型对于组合模型的影响。下文简称使用IGS公布数据的BP神经网络与AR模型的组合模型(combined model of BP neural network and AR model using IGS data)为BA模型，使用经过卡尔曼滤波数据的BP神经网络与AR模型的组合模型(combined model of BP neural network and AR model based on Kalman filter data)为KBA模型[19]。图2为这2种模型的流程图。

选择的精度验证方法是残差V分布情况和均方根(root mean square，RMS)，即

V=pi-qi。

(9)

式中：pi为不同预测模型的预测数据；qi为IGS网站公布的实际TEC数据。

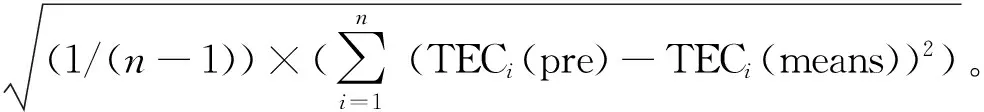
(10)

式中：TECi(pre)为预测数据；TECi(means)为实际数据；n为预测TEC数据的个数。

2 实验与结果分析

使用IGS网站下载的2015年电离层网格点TEC数据对该方法进行分析。考虑自2015年全球网格点数据以1 h为时间间隔(1 d共24个观测值)，限于篇幅，选用2015年4个月份前10 d数据，这些数据的可预测性处于平均水平。为验证该方法是否与数据的时间和纬度有关，取年积日为第1天至第10天、第90天至第100天、第181天至第191天、第273天至第283天，经纬度为(87.5°N，125°E)、(45°N，125°E)、(0°N，125°E)。利用BA模型和KBA模型对上述基础数据进行提前1 d的预报。图3为年积日为第181天至第190天电离层TEC原始数据与卡尔曼滤波后的数据对比，可以看出通过卡尔曼滤波后的电离层TEC数据仍然保持原始数据的变化趋势，但是相对原始数据更加平缓(电离层TEC的计算单位为TECU，1个TECU表示每平方米有1016个电子)。

使用第1天至第9天数据进行滤波前后模型的对比，图4至图6分别表示 87.5°N、 45°N、赤道数据在滤波前后建模预报的情况。

统计预测值的残差分布和RMS值结果如表1所示。

表1 不同纬度的残差(V)分布与均方根(RMS)比较情况(1月)

由表1可知：比较1月份各个纬度的预测情况，使用BA模型完成预测，残差在±2个TECU以内的预测值比例占36 %，残差值小于±1个TECU的预测值比例占25 %，残差平均值为-1.725 9个TECU；使用KBA模型完成预测，残差在±2个TECU以内的预测值比例占41.67 %，残差值小于±1个TECU的预测值比例占25 %，残差平均值为-0.654 9个TECU。结合图4～图 6，组合模型对于数据具有较好的预测作用，使用经过卡尔曼滤波的数据与直接使用原始数据进行预测相比，预测值曲线变化的趋势非常接近，使用经过卡尔曼滤波的数据完成建模和预报，残差分布优于直接使用原始数据进行建模和预报，且使用经过卡尔曼滤波后的数值进行预测，预测结果的RMS值更小，拟合程度更好。

使用第90天至第99天的数据进行滤波前后组合模型的对比，图7～图9分别表示4月87.5°N、 45°N、赤道数据在滤波前后建模预报的情况。

统计预测值的残差分布和RMS值结果如表2所示。

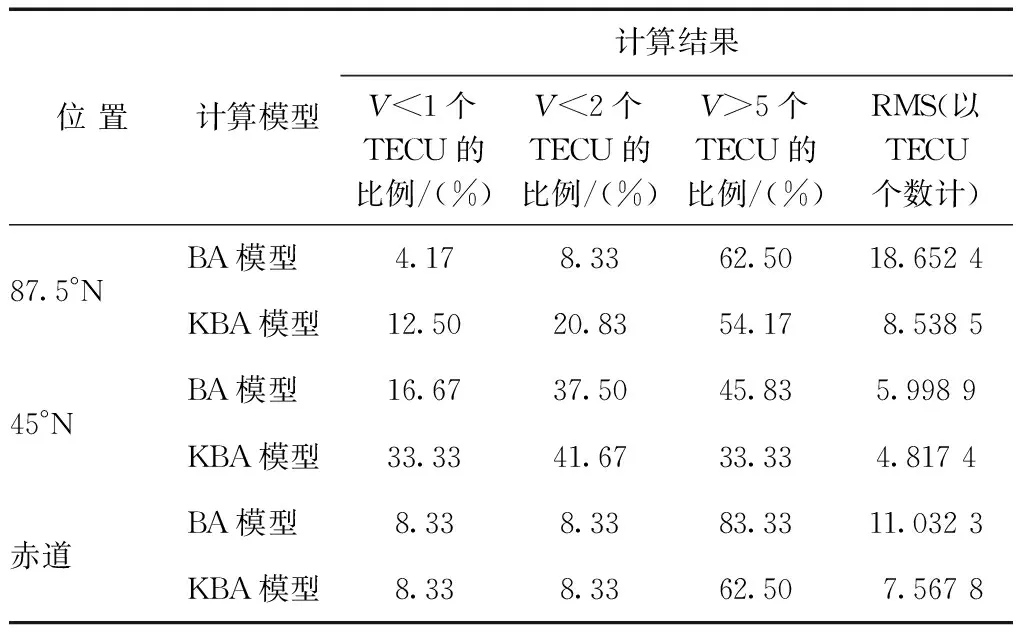
表2 不同纬度的残差(V)分布与均方根(RMS)比较情况(4月)

由表2可知：使用BA模型预测，残差在±2个TECU以内的预测值占总预测值的18.05 %，残差在±1个TECU以内的预测值占总预测值的9.72 %；使用KBA模型完成预报，预报残差值小于±2个TECU的预测值比例占23.61 %，残差在±1个TECU以内的预测值占总预测值的18.05 %以上。结合图7～图9，BA模型和KBA模型对于数据都具有较好的预测作用，而KBA模型预测值相对BA模型预测值在残差平均值、残差分布和RMS值等方面占优，表示KBA模型预测值拟合程度更好。

使用第181天至190天数据进行滤波前后组合模型的对比，图10～图12分别表示7月87.5°N、45°N、赤道数据在滤波前后建模预报的情况。

统计预测值的残差分布和RMS值结果如表3所示。

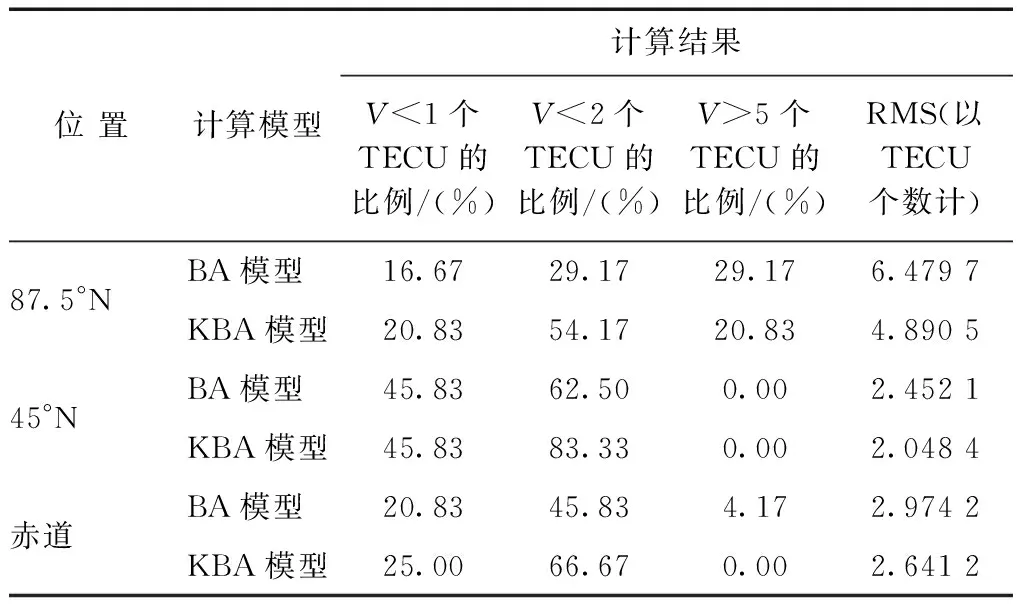
表3 不同纬度的残差(V)分布与均方根(RMS)比较情况(7月)

由表3可知：使用BA模型完成预测，残差在±1个TECU以内的预测值占总预测值的 27.78 %，RMS值为3.968 6个TECU，残差平均值为-1.439 4个TECU；使用KBA模型完成预报，预报残差值小于±1个TECU的预测值比例占30.55 %，RMS值为3.193 3个TECU，残差平均值为-0.938 7个TECU。结合图10～图12，组合模型对于数据具有较好的预测作用，BA模型和KBA模型预报数据曲线变化趋势与实际数据非常接近，且KBA模型残差统计方面和RMS值均优于BA模型，因此KBA模型相对BA模型具有更好的预测能力。

使用第273天至第282天数据进行滤波前后组合模型预测，图13～图15分别表示10月87.5°N、45°N、赤道建模预报的情况。

统计预测值的残差分布和RMS值结果如表4所示。

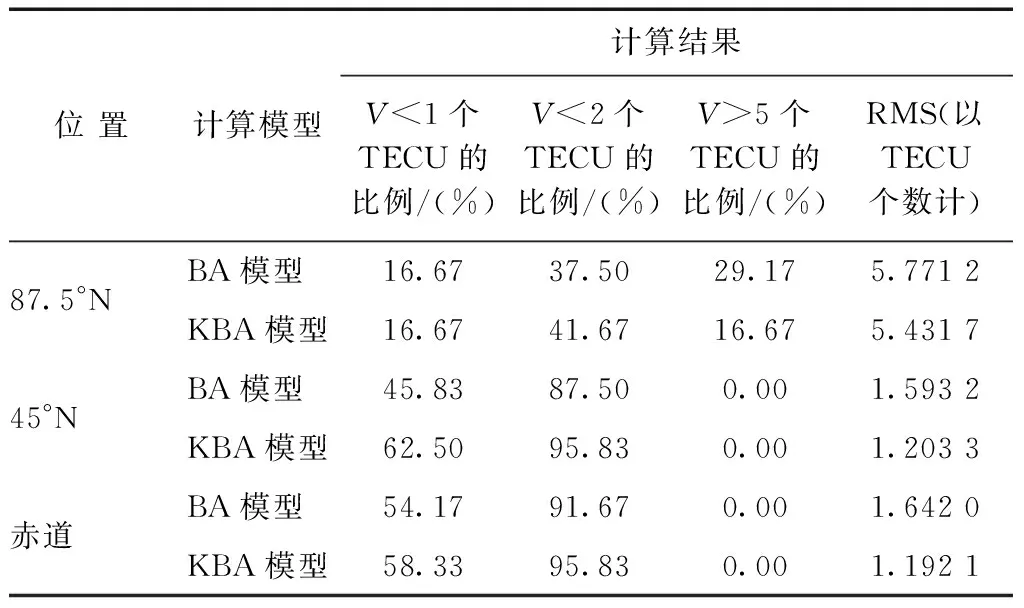
表4 不同纬度的残差(V)分布与均方根(RMS)比较情况(10 月)

由表4可知：BA模型残差在±2个TECU以内的预测值比例占72.22 %，残差值小于±1个TECU的预测值比例占38.89 %，残差平均值为-0.944 2个TECU；KBA模型残差在±2个TECU以内的预测值比例占77.78 %，残差值小于±1个TECU的预测值比例占45.83 %，残差平均值为-0.298 1个TECU。KBA模型RMS的平均值为2.609 0个TECU，BA模型RMS的平均值为3.002 1个TECU。RMS值越小精度越高，表示使用经过滤波后的数据生成模型具有更高的预报精度。

3 结束语

本文采用卡尔曼滤波对IGS公布的电离层TEC值进行预处理，再使用AR模型和BP神经网络模型得到的组合模型进行建模和预测。原始数据通过滤波能够降低原始状态偏差的影响，得到更高精度的状态估值，再利用高精度状态值进行建模和预报。通过实验证明，使用卡尔曼滤波处理原始数据不仅保持了数据趋势性，而且使用处理后的数据进行建模，模型预测精准度更高。KBA模型在残差值大小、残差分布和RMS值方面均优于BA模型，表示KBA模型相对BA模型具有更高的预报精度；KBA模型在中低纬度预测更加精准，且10月是实验部分中预测精度最高的月份。将卡尔曼滤波应用于预测模型预处理为模型的建立提供了新的思路。

[1] RATNAM V D，DINESH V B，TEJASWI B，et al.TEC prediction model using neural networks over a low latitude GPS station[J].International Journal of Soft Computing and Engineering，2012，2(2)：2231-2307.

[2] 张小红，任晓东，吴风波，等.自回归移动平均模型的电离层总电子数含量短期预报[J].测绘学报，2014，43(2)：118-124.

[3] 李磊，张淑芳，王轶卓，等.利用ARMA模型进行电离层TEC预报[J].应用基础与工程科学学报，2013，21(5)：814-821.

[4] 孙佳龙，郭金云，郭淑艳.利用夹角余弦和聚类分析的电离层TEC混沌预测[J].武汉大学学报(信息科学版)，2014，39(4)：441-456.

[5] 李淑慧，彭军还，徐伟超，等.利用神经网络预报短期电离层TEC变化[J].测绘科学，2013，38(1)：8-12.

[6] 陈鹏，姚宜斌，吴寒.利用时间序列分析预报电离层TEC[J].武汉大学学报(信息科学版)，2011，36(3)：267-270.

[7] 卢辰龙，匡翠林，张晋升，等.组合SSA与ARMA模型预报电离层TEC[J].大地测量与地球动力学，2014，34(6)：44-49.

[8] 王建敏，黄佳鹏，祝会忠，等.电离层总电子数预报方法研究[J].测绘科学，2016，41(12)：47-53.

[9] 李奕.自适应卡尔曼滤波在变形监测数据处理中的应用研究：以太原万达广场A2区基坑监测为例[D].成都：成都理工大学，2012.

[10] 宋雪航，史良胜，杨金忠.基于集合卡尔曼滤波的潜水动态预测方法[J].武汉大学学报(工学版)，2015，47(3)：324-331.

[11] 魏二虎，张帅，WEI Jianan.自适应滤波在环火探测器脉冲星自主导航中的应用[J].武汉大学学报(信息科学版)，2015，40(5)：701-705.

[12] 李秀海，郭达志.应用半参数AR模型的电离层TEC建模与预测[J].测绘科学，2011，36(2)：149-151.

[13] 李捷斌，孔令杰.基于Kalman滤波的BP神经网络方法在大坝变形预测中的应用[J].大地测量与地球动力学，2009，29(4)：124-126.

[14] HABARULEMA J B，MCKINNELL L A，CILLIERS P J.Prediction of global positioning system total electron content using neural networks over South Africa[J].Journal of Atmospheric and Solar-Terrestrial Physics，2007，69：1842-1850.

[15] 田间.一种训练BP神经网络的融合算法[D].长春：吉林大学，2011.

[16] 王德明，王莉，张广明.基于BP神经网络的短期风速预报模型[J].浙江大学学报(工学版)，2012，46(5)：837-841.

[17] 李聪.基于BP神经网络的股票指数期货价格预测[D].青岛：青岛大学，2015.

[18] 闪丽洁，张利平，刘恋，等.基于多方法优选因子和人工神经网络耦合模型的枯水期径流预报[J].武汉大学学报(工学版)，2015，48(6)：758-763.

[19] 赵传华，党亚民，秘金钟.组合方法在电离层TEC短期预报中的应用[J].大地测量与地球动力学，2012，32(3)：76-79.