不同结构体系钢管混凝土框架地震响应对比
2018-03-05陈强
陈 强
(福建省金亿建设工程有限公司 福建福州 350001)
0 引言
钢管混凝土能够适应大跨度、高耸结构、大载荷等特点要求,具有优越的力学性能和先进的经济技术指标,被广泛应用于现代土木工程建造中[1]。国内外学者对钢管混凝土结构进行了大量(拟)静力试验研究,但结合振动台进行地震模拟试验则较少。而上部结构与地基土是一个共同工作的整体系统,在地震荷载作用下,二者相互作用(称为土-结构相互作用,简写为SSI)[2-3]。由于考虑SSI作用的上部结构体系比刚接体系的刚度要低,频率增大,在软土地基,其差异更加明显,且目前对于钢管混凝土框架结构的抗震性能影响研究又较少[4-6],为获得钢管混凝土框架结构地震响应规律,本文进行了刚接、考虑SSI两种情况的数值模型试验,并分析两种体系在不同地震波作用下的地震响应变化规律,为工程结构设计提供参考。
1 钢管混凝土框架结构体系模型的建立与验证
1.1 试验模型设计


(a)刚接结构 (b)SSI结构图1 不同结构试验模型
试验采用加速度传感器来采集结构的动力响应,主要采用的实验仪器有INV-306DF智能信号采集处理分析仪、INV-16多功能抗混滤波放大器、INV9818系列压电加速度传感器,使用频率范围为0.2-1500Hz,灵敏度较高[7-8]。根据Shannon采样定理,确定试验采样频率为512Hz,对结构分别进行不同激励点的力锤激励测试,以得到典型的加速度时程曲线[9-10]。
1.2 建立有限元模型
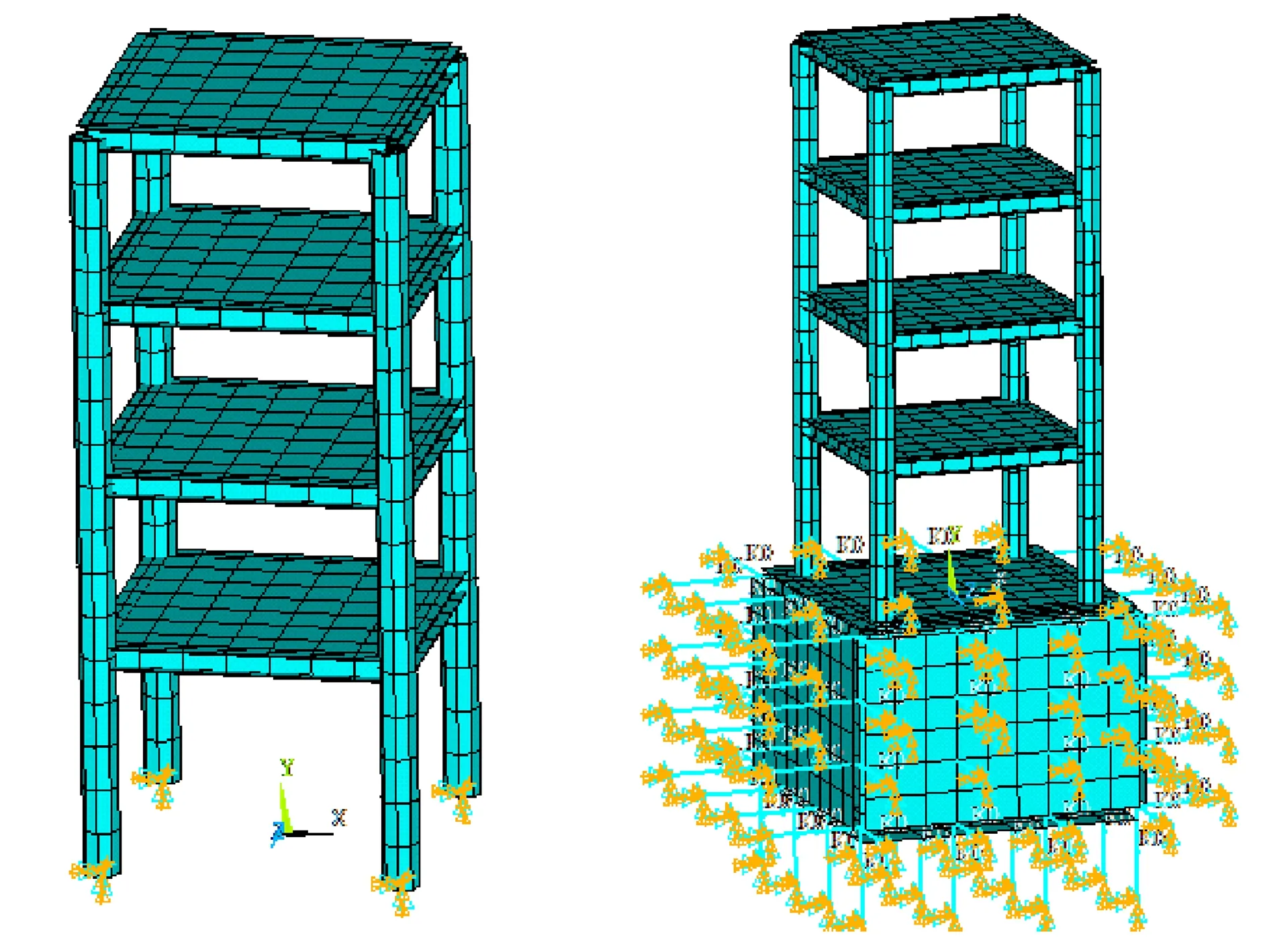
(a)刚接结构 (b)SSI结构图2 不同结构有限元模型
采用ANSYS建立有限元模型,将刚性结构体系模型底部4个支座设置为完全约束,而将考虑SSI的结构体系箱基四周与底部土体设置为弹簧-阻尼单元。模型计算时,箱基、土体、钢管砼柱、钢梁、楼板等结构体系弹性模量、泊松比、密度等参数取值与实际工程一致,有限元模型建立如图2所示。
1.3 模型验证
结合模型试验与有限元数值分析两种手段,对考虑与不考虑SSI影响的两种结构体系进行模态分析,得到结构前7阶频率对比,如表1所示。

表1 两种模型结构不同模态阶次实测频率对比
注:SZ——数值分析;SY——试验实测。
从表1可以看出,数值分析和试验实测中未测出刚接结构第6阶频率。为了更直观地说明,取两种结构前三阶模态和SSI结构第六、七阶模态进行分析,如图3~图5所示。

(a)第一阶模态 (b)第二阶模态 (c)第三阶模态图3 刚接结构前3阶模态图
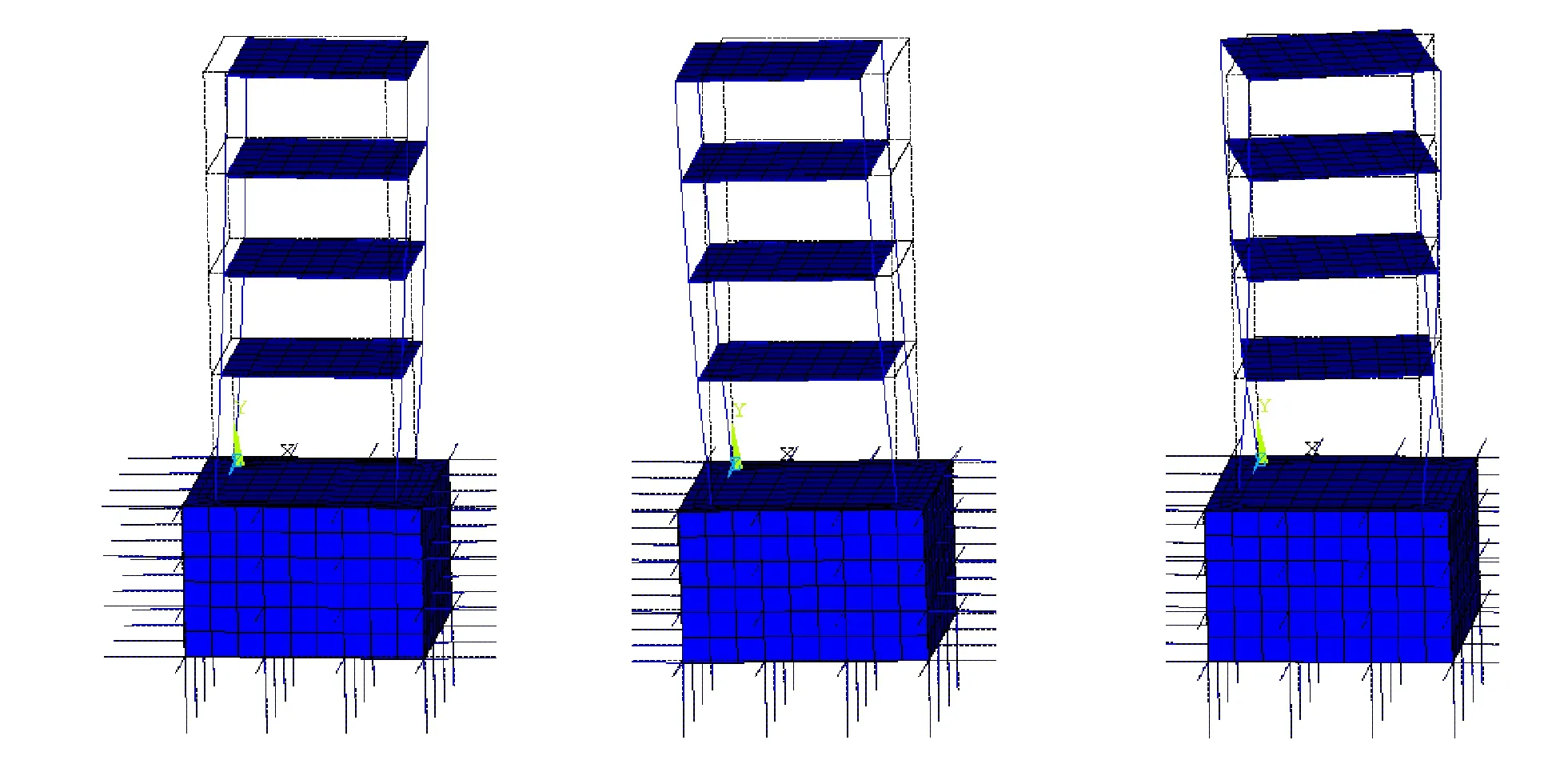
(a)第一阶模态 (b)第二阶模态 (c)第三阶模态图4 考虑SSI结构前3阶模态
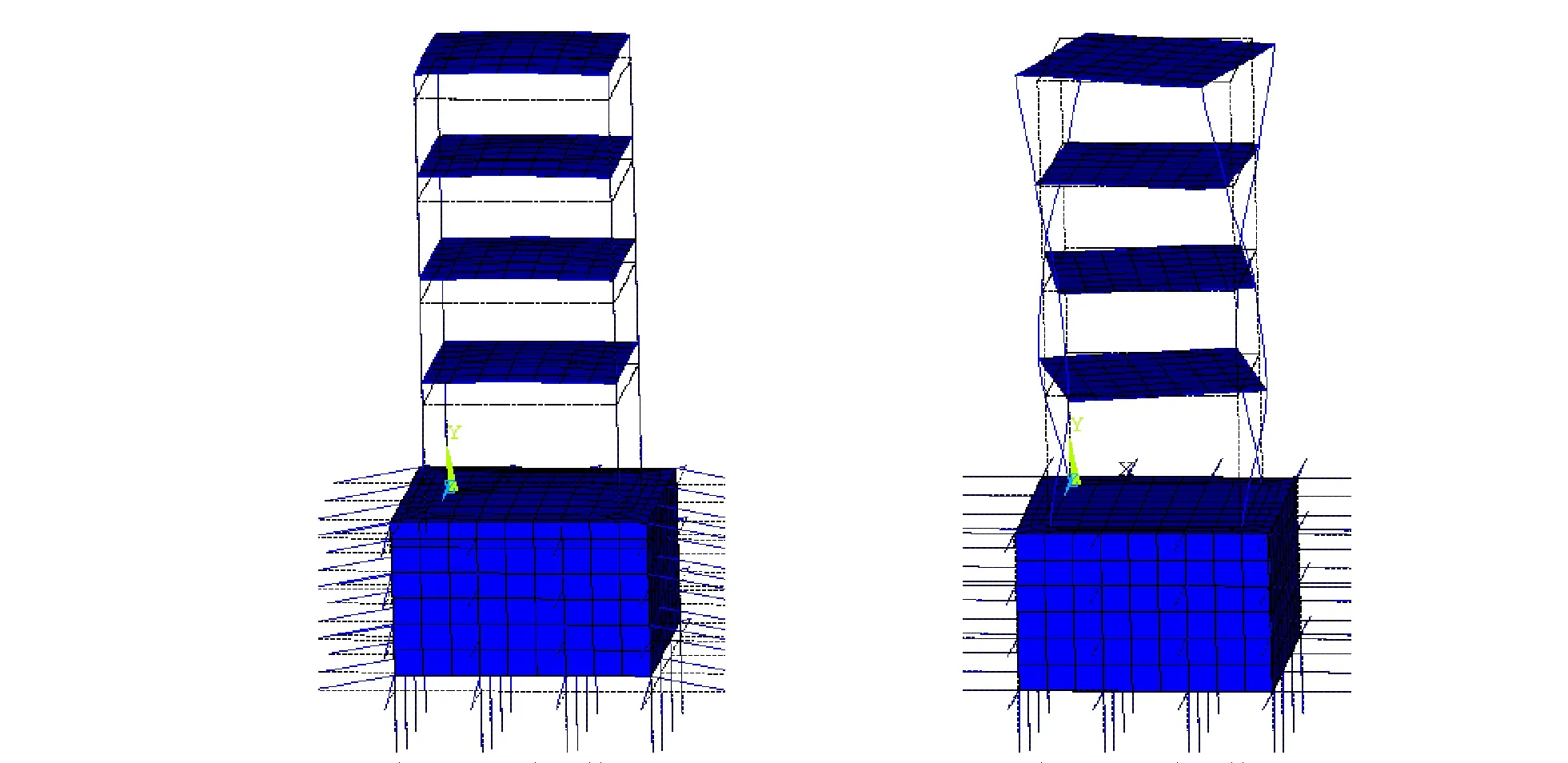
(a)第六阶模态 (b)第七阶模态图5 考虑SSI结构的第6、7阶模态
从图4可以看出,由于结构平面为双轴对称,SSI结构X和Z两个方向一、二阶平动模态频率是相等,三阶为扭转变形。
由图5可以看出,考虑SSI作用的结构在第六阶出现竖向变形,而在刚接结构中不会出现此现象,SSI结构的第七阶应与刚接结构的第六阶对应。因为刚接结构底部是完全约束,不会产生竖向提离现象,然而由于土体可产生压缩变形,因此在考虑SSI结构中产生竖向提离现象是符合实际。
由表1可以得出,考虑SSI结构比刚性结构自振周期增大,频率则降低,SZ方向频率最大降低10.4%,SY方向频率最大降低10.9%。
对比模型试验与有限元数值结果,获得在低阶模态数值分析的结果更为逼近实测模态试验。可见,考虑与不考虑SSI影响的两种结构体系有限元模型与试验模型是比较接近,证明所建立的二重结构体系有限元模型是有效的。
2 不同结构体系地震响应分析
2.1 参数选取
为了更精确地分析实际工程结构的地震响应情况,本文在验证上述按1∶10比例缩尺建立的有限元模型有效性的基础上,采用相同的有限元建模方法,建立了1∶1比例尺的实际工程结构尺寸的有限元模型。共建立了4层、8层、12层3组不同楼层高度的结构有限元模型,并分别对这3组结构进行非线性地震响应数值分析。
本文进行结构地震响应时程分析时,选用2组实际强震记录El Centro、阪神波和1组上海人工波。其中,El Centro最大加速度峰值为341.7cm/s2,持续时间为30s;阪神波最大加速度峰值为817.82cm/s2,持续时间为20s;上海人工波最大加速度峰值为156.86cm/s2,持续时间为24.9s。
2.2 楼层变化对比
经过有限元模态分析,得到4层刚接结构的一阶、二阶自振频率为2.26Hz,周期为0.44s,考虑SSI的4层结构一阶、二阶自振频率为1.50Hz,周期为0.67s;8层刚接的钢管混凝土框架结构一阶、二阶自振频率为1.04Hz,周期为0.96s,考虑SSI的8层结构一阶、二阶自振频率为0.70Hz,周期为1.43s;12层刚接的钢管混凝土框架结构一阶、二阶自振频率为0.67Hz,周期为1.49s,考虑SSI的12层结构一阶、二阶自振频率为0.42Hz,周期为2.38s。
2.2.1不同结构水平最大位移对比
计算获得了不同结构、不同地震波作用下顶层最大水平位移,图6所示为12层结构在不同地震波作用下顶层最大水平位移,图7为不同层数结构在不同地震波作用下各层最大水平位移对比。不同结构计算结果对比如表2所示。

(a)El Centro
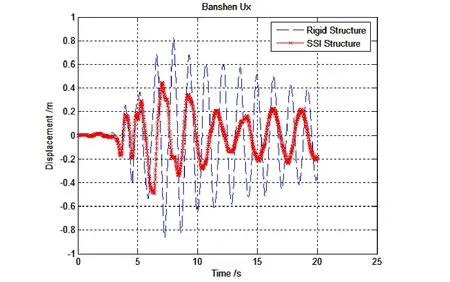
(b)阪神波

(c)上海人工波
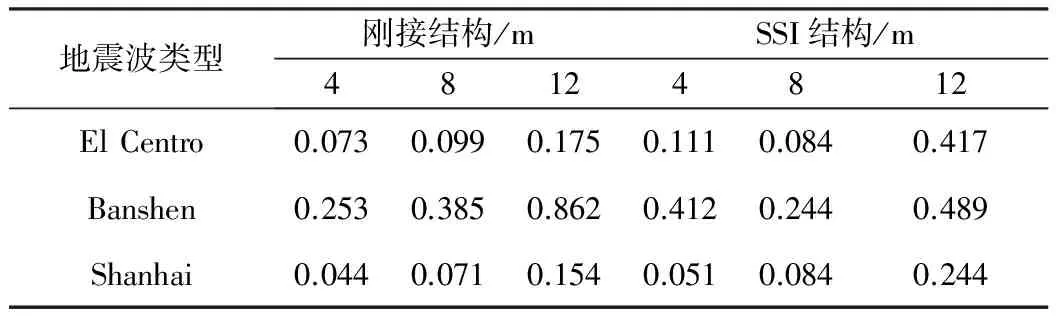
地震波类型刚接结构/mSSI结构/m48124812ElCentro0.0730.0990.1750.1110.0840.417Banshen0.2530.3850.8620.4120.2440.489Shanhai0.0440.0710.1540.0510.0840.244

(a)4层楼在不同地震波下最大水平位移

(b)8层楼在不同地震波下最大水平位移
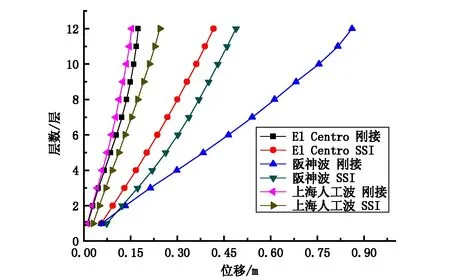
(c)12层楼在不同地震波下最大水平位移
2.2.2对比结果分析
结构的自振频率随着楼层高度的增加而减小,自振周期则随着楼层高度的增加而增大。不同楼层高度的地震响应情况有所不同,结构的变形并不均是随着楼层高度的变化而成线性变化,并非楼层高度越高地震响应越大。在3组地震波作用下,不考虑SSI的刚接结构的最大变形均随着楼层高度的增加而增大。然而考虑SSI的4层和8层结构在El Centro和阪神波作用下,4层结构的最大水平位移变形略大于8层结构,在上海人工波作用下,8层结构的最大水平位移要大于4层结构。而对于12层结构来说,不管是否考虑SSI作用,其结构最大变形均大于4层或8层的结构。
2.3 地震响应分析
结构体系地震响应情况与地震性特征有着密切的联系,即使同一个结构体系在不同的地震波作用下响应情况也不完全相同。8层的结构体系在El Centro和阪神波作用下,考虑SSI的钢管混凝土框架结构体系比不考虑SSI的位移有所减小,而在上海人工波作用下,考虑SSI的比不考虑SSI的位移反应要大。这表明不同的结构体系即使在相同的地震波作用下反应也不一定相同,主要是因为耦联系统的频率、模态等振动特性因相互作用而发生变化。变化后的频率如果与输入地震波的主要特征周期范围非常接近,则可使反应加大,反之减少[11]。从3组地震波的加速度反应谱来看,El Centro主要特征周期范围集中在0~1s,阪神波的主要特征周期集中在1s以内,上海人工波的主要特征周期达2s。考虑SSI的钢管混凝土框架结构体系的特征周期达到1.43s,超出了两组实际记录的地震波特征周期范围,但并未越出上海人工波的特征周期范围,从而在两组实际记录地震波作用下,考虑SSI的反而减小。考虑SSI作用可使结构体系的频率减小,自振周期增大,阻尼比增大,这与前人的研究结果基本一致[12-13]。
3 抗震性能评价
通过对不同地震波作用下两种结构体系地震响应对比分析,由图7可以得出4层结构体系各楼层最大位移曲线无明显转拆点,表明结构没有明显破坏,钢管与混凝土二者之间工作性能良好。
从8层结构体系各楼层最大位移曲线来看,在El Centro作用下的刚接结构体系在一层处出现一个小转折点,曲线略向右倾斜,但基本保持在直线附近,可见在该地震波作用下不考虑SSI的钢管混凝土框架结构体系出现轻微损伤。在阪神波作用下,不考虑SSI的结构体系在一层处出现明显的转折点,曲线严重向右倾斜,结构体系的侧向刚度明显下降,这表明在阪神波这种强烈的地震波作用下,结构会发生严重的损伤,而考虑SSI的结构体系的各楼层最大位移曲线基本保持直线状态,表明结构的侧向刚度没有发生明显改变,结构体系保持良好的工作状态。在上海人工波作用下,两种结构体系的各楼层最大位移曲线基本为直线,结构体系没有产生破坏。
从12层结构体系各楼层最大位移曲线来看,在El Centro和上海人工波作用下,结构体系的刚度无明显退化,结构体系无明显的破坏。在阪神波作用下,不考虑SSI的结构体系同样在一层处出现转拆点,曲线向右倾斜,结构刚度发生明显的改变,结构产生了破坏,然而考虑SSI的结构体系确没发生明显的破坏现象。
4 结语
通过对两种钢管混凝土结构体系进行模型试验与数值计算分析研究,得到如下结论:
(1)考虑SSI的钢管混凝土框架结构在高阶模态会产生提离现象,而不考虑SSI的刚接结构不会产生提离现象。
(2)考虑SSI的钢管混凝土框架结构比底部刚接结构体系自振频率减小,自振周期增大。
(3)4层钢管混凝土框架结构体系在3组地震波作用下均未产生破坏,抗震性能良好。而不考虑SSI的8层、12层结构体系在阪神波作用下,在一层处出现刚度退化转折点,表明一层为结构的薄弱层,在抗震设计时应适当的加固。
[1] 钟善桐.钢管混凝土结构[M].北京:清华大学出版社, 2003.
[2] 冯锋杰.基于接触弹簧模型的土与上部结构相互作用的动力特性研究[D].安徽:合肥工业大学, 2007.
[3] 张俊胜.土-结构动力相互作用的研究方法和发展趋势[J].外建材科技, 2005, 26(1): 52-54.
[4] 杜国锋, 许成祥, 余俊凯.钢管混凝土框架模型地震反应有限元分析[J].四川建筑科学研究, 2007, 33(5): 103-105.
[5] 张文福, 赵文艳.方钢管混凝土双向压弯截面非线性分析算法[J].黑龙江工程学院学报, 2001, 15(6): 13-15.
[6] 彭轶君, 尚守平, 朱志辉, 等.有限元模拟土-箱基-框架结构大比例模型动力相互作用研究[J].铁道科学与工程学报, 2006, 3(1): 75-79.
[7] 尚守平, 朱志辉, 涂文戈, 等.土-箱形基础-结构动力相互作用的模态试验分析[J].湖南大学学报, 2004, 31(5): 71-76.
[8] 周云, 易伟建.考虑土-结构动力相互作用的框架结构的参数识别研究[J].土木工程学报, 2007, 40(6): 14-19.
[9] 姜绍飞, 陈强, 吴兆旗.考虑SSI的钢管混凝土框架结构易损性分析[J].武汉理工大学学报, 2010, 32(9): 213-217.
[10] 姜绍飞, 杜权, 吴兆旗.考虑SSI影响的钢管混凝土框架h模态分析[J].华中科技大学学报, 2008, 25(3): 27-30.
[11] 汪梦甫, 汪加武.考虑土-结构相互作用高层框架结构非线性地震反应分析[J].湖南城市学院学报(自然科学版), 2004, 13(2): 1-4.
[12] Murat P, Naci C,Muzaffer E, Abdulkadir C, et al.Dynamic soil-structure interaction analysis of buildings by neural networks [J].Construction and Building Materals, 2008, 22: 330-342.
[13] Mofid N, Mohammad AG.The effect of soil-structure interaction on damage index of buildings[J].Engineering Structures, 2008, 30: 1491-1499.
