匀强磁场中任意刚性导线的动生电动势
2018-03-05陈余华
陈余华
(江西省大余中学 江西 赣州 341500)
黄亦斌
(江西师范大学物理与通信电子学院 江西 南昌 330022)
磁场中导体运动导致的动生电动势是电磁感应的一个重要内容.而动生电动势的计算也是高考和竞赛的重要考点,也是大家讨论的一个热点[1].文献[2]研究了较为一般的情况,即刚性直导线在垂直于匀强磁场的平面内绕任一固定点旋转.其结论是,无论固定点在哪里,导线中的电动势都由其中点速度决定,并给出公式和相关证明.
本文欲将其结论推广到更一般的情形,包括直导线的任意运动以及任意形状的刚性导线的任意运动,并对结果给出更为严格和简短的证明.
1 出发点
讨论的出发点是一段导线微元dl在磁场中运动时产生的电动势
dE=v×B·dl
(1)
该式不仅给出了电动势dE的大小,也给出了其符号,而且以沿dl方向为正.根据矢量混合积的性质,该电动势等于3个矢量v,B,dl所构成的平行六面体的体积(可相差一个负号),如图1所示.如果v,B,dl构成右手系,则dE>0;若三者构成左手系,则dE<0.当然,如果v,B,dl中有任何两个方向相同(或相反),则dE=0.所有这些都与动生电动势的通常判断结果(包括大小和方向)相同.

图1 混合积v×B·dl
还需对刚体的运动做一陈述.在刚体上取一点D,称为基点,则刚体的任一运动状态可视为随基点的平动和绕基点的转动的合成.平动由vD表征,转动由角速度ω表征.这里的角速度矢量沿转轴,且由右手螺旋法则确定:伸出右手,让四指绕向与旋转方向一致,则大拇指的指向就是角速度的方向.这样,刚体上任一点P的速度为
v=vD+ω×r
(2)
其中r为点P相对于点D的位置矢量.基点可以任取,从而vD和r随之变化;但无论取哪一点为基点,刚体的角速度ω是确定的.
2 直导线做任意运动时产生的电动势
结论一:刚性直导线在匀强磁场中做一般运动时产生的电动势,等于它以中点速度做平动而产生的电动势
E=B×l·vC=B·l×vC
(3)
如果导线限制在某平面内运动(比如垂直于磁场的平面,即文献[2]所考虑的情形),那么此时可以用图2来对结论一进行说明.导线从位置AB运动到A′B′时扫过的面积,与导线仅做平动而运动到A″B″时所扫过的面积,二者显然相等.故两种运动所切割的磁通量相同,电动势相同.

图2 做平面运动的直导线
对于更一般的情形,可对结论一做如下说明:在中点两边对称地取两段微元,它们的速度都是中点速度加上相对于中点的速度.它们的后一相对速度一定相反,对总电动势的贡献相反,从而只剩下各自的中点速度导致的贡献.由于相对运动的效应成对抵消,故而最终只剩下共同的、中点速度导致的效应.
结论一的严格证明如下.
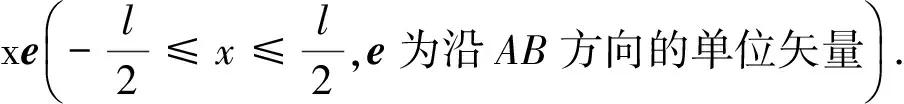
v=vC+ω×xe
(4)
将其代入式(1),考虑到微元为dl=dxe,积分,并注意vC,ω,e,B在积分时都是常矢量,得
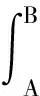
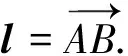

EAB=BLvCcosθ=ωBS
(5)


图3 处于匀强磁场中的导线
3 一般闭合回路中的电动势
结论二:对于匀强磁场中任意形状的刚性线圈,其做任意运动时的总电动势为
E=B·S×ω=B×S·ω
(6)
其中S为其面积矢量.
这里先对面积矢量作些说明.
(1)面积矢量仅对回路才有定义.不闭合的导线没有“面积矢量”一说.
(2)对于平面回路,其面积矢量的大小就是回路面积的大小,其方向沿回路平面的法向,且由右手螺旋法则确定:四指绕向与回路的绕向(电流或电动势的正方向)相同,则大拇指的方向即为S的方向.

(4)N匝线圈的面积矢量是单匝线圈的面积矢量的N倍.如果匝与匝之间距离较大,或者线圈的绕行相当任意,那么可用下面的一般公式定义其面积矢量
(7)

(5)回路的面积矢量显然跟原点的位置无关,而式(7)正满足这一条,虽然表面上它似乎跟原点的位置有关.这是因为,原点换成O′时,r′=r+rO(图4).由于rO为常矢量,故
dr′=dr
于是
其中用到了∮dr=0.

图4 面积矢量
对于常见的矩形线圈旋转产生电动势的问题中,当线圈平面与B平行时,线圈的电动势最大,且最大值为BSω.用式(6)来解释,那是因为此时B,S与ω两两垂直.仔细分析还表明,式(6)也正确反映了电动势的方向(注意电动势的正方向就是回路的绕向).而图3中的回路ABODA的电动势依式(6)计算为
E=Bey×[-S(ex+ey)]·ωez=BSω
(8)
当然,式(8)也可以通过分析回路每段的电动势而得到.
可以根据式(6)来判断线圈的电动势何时为零.这包括以下情形:
(1)ω=0,即线圈只做平动,无转动;
(2)ω,B同向,即线圈的转轴沿磁场方向;
(3)ω,S同向.对于平面线圈而言,这意味着线圈的转轴垂直于线圈平面;

结论二的证明如下.
任取线圈刚体的基点D,把式(2)代入式(1),积分,得
E=∮dE=∮(vD+ω×r)×B·dr=
vD×B·∮dr+∮dr×(ω×r)·B
其中vD,ω,B为常矢量,而
dr×(ω×r)=ω(r·dr)-(ω·dr)r=
其中rr为并矢(二阶张量).由于
故
S×ω·B=B×S·ω
其中,用到了面积矢量的定义(7).证毕.
4 任意形状的导线中的电动势
结论三:对于任意形状的刚性导线ALB,其在匀强磁场中运动时产生的动生电动势由两部分构成:直导线AB的电动势和回路ALBA的电动势,即
EALB=EALBA+EAB
(9)
该结论的证明非常简单,几乎不需要文字说明,仅图5足矣.

图5 一般刚性导线的电动势
于是,根据结论一和结论二,导线ALB的电动势为
EALB=B×S·ω+B×l·vC
(10)

对于直导线,式(9)和(10)的第一项为零;对于闭合线圈,它们的第二项为零. 而对于图3中非闭合的空间导线BODA,根据结论三,其电动势应该为回路BODAB的电动势与直线BA的电动势之和.前者由式(8)给出,后者与式(5)相反,故导线BODA电动势为零.(当然,直接分段考虑也可得到该结论.)
1 杨培军,王鹏.数学平均值在物理上的应用.物理通报,2015(5):22~25
2 徐洪图,窦人镜.导体棒转动切割磁感线问题探微.物理通报,2017(3):52 ~ 53
