基于反激式变换器的锂电池组均衡策略

2018-03-05黄梦涛张帅

蓄电池 2018年1期

黄梦涛，张帅

（西安科技大学电气与控制工程学院，陕西西安 710054）

0 引言

由于目前制造工艺的限制，单体锂电池最高电压与设备额定电压相距甚远，因此往往需要通过串并联成组来满足动力设备对电压、功率和续航的需求[1-2]。然而，电池成组使用后，由于单体电池自身体的因素，加之温度、充放电电流等外界环境的影响，电池组实际使用容量远远达不到预期[3]，严重影响了电池组的日历寿命[4]。并且，在电池组中由于不一致性引起的某一单体电池的过充、过放会也对电池的循环寿命造成不可逆的影响。因此，需采取有效的均衡策略来延长电池组的日历寿命，增加电池在达到寿命终止条件前能够执行的循环次数。

1 现有均衡方案分析

目前，主流的均衡方式分为能量耗散型与能量转移型。能量耗散性方案主要是采用电阻对电压较高的电池进行放电，直到与低电压的电池相近，实现单体电池之间电压相同。这种均衡方案结构简单，但是均衡过程中会产生大量的热量，并且会浪费能源[5]。能量转移型均衡方案主要通过能量在电池间转移，达到均衡的目的。近年来，国内外提出了一些新的能量转移性均衡方案。例如，以碳基双电层电容器作为新的储能系统，以开关控制旁路电容的开关电容法。与该方法类似的还有电感均衡法，如 Buck-Boost 转换模型、Cuk 转换模型。此类方法能耗少，效率高，但电容与电感的时滞使得均衡频率受限，同时电容与电感需求量大。文献 [6]中设计了一种基于反激式变换器的锂电池组均衡系统，能够通过整组电池向剩余电量较低的电池进行能量转移，均衡速度快，能量损失小。其均衡策略为：单体电池容量大于平均容量且两者之差超过设定值时，对其进行放电均衡；单体电池容量小于平均容量且两者之差超过设定值时，对其进行充电均衡。若按照文献 [6]中的均衡原则，得到的结果如表 1 所示。

表1 均衡结果 %

通过表 1 可以看出，在均衡过程中反复对电池充放电，并且通过 6 次均衡才能使电池组中单体电池间的差距缩小到 1 % 以下。很明显，这种均衡策略存在对低电量电池反复充放电，耗能增加，均衡速度慢等问题，导致电池与 MOS 管的寿命缩短。因此，有必要设计一种更为全面的均衡策略，充分发挥反激式变换电路的优势，提高均衡效果。

2 电池组均衡电路和工作原理

在图 1 所示均衡电路中：每一只单体电池都会并联一个 MOS 管和一个反激式变压器；每个变压器的原边都与电池组的正、负极相连，副边通过开关与各只单体电池的正、负极相连；开关管由均衡控制单元驱动，通过控制原边与副边的导通顺序，即可控制能量的传输方向[7]。假设电池 BT2 中的剩余电量低于平均值，则对电池 BT2 充电均衡电路如图 2 所示。首先，导通开关 N2，通过电池组向变换器 T2 的原边充电，初级绕组中的电流逐渐上升；然后，当电流到达设定值时，关断开关 N2，停止对初级绕组充电，同时导通开关 M2，使存储在初级线圈中的能量向次级线圈中转移，并对电池BT2 进行充电。

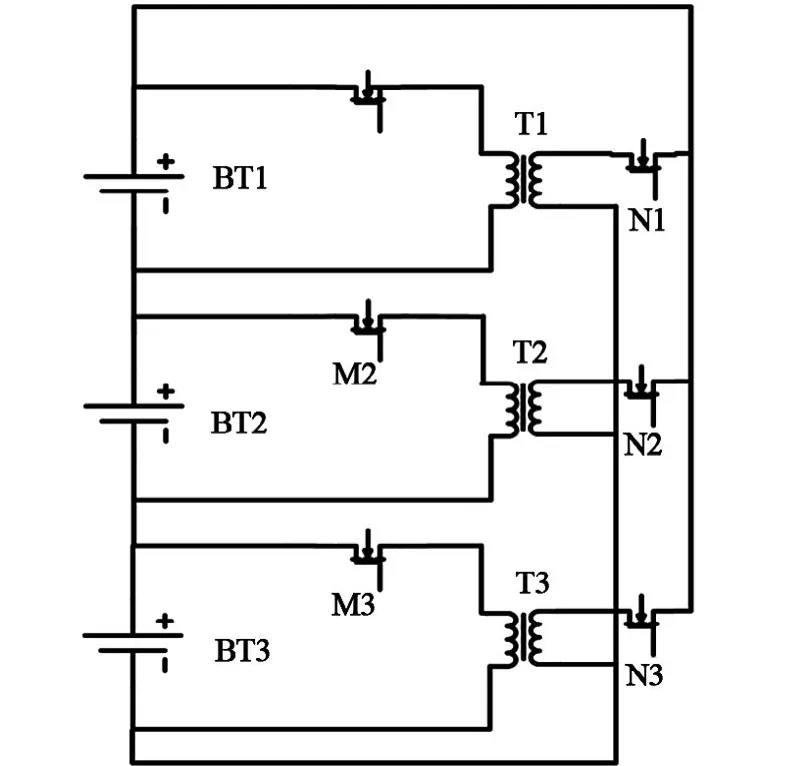
图1 均衡电路

图2 对电池 BT2 均衡的等效电路

3 电池组均衡策略

3.1 均衡依据

在电池组均衡策略中，均衡依据的选择对均衡的效果至关重要。传统的方法是以电池电压作为均衡依据。虽然电池电压容易获得，但由于单体电池的内阻不同，电流的剧烈变化将引起电池端电压上下浮动，端电压变化不具有稳定性，以端电压一致作为均衡标准在电流急剧变化的工况下容易导致对某些电池反复充放电。使用 SOC 值作为均衡依据不仅可以更加精确地计算需要均衡的电荷量，而且可以消除反复充放电的问题。电荷累积法是一种较为简单的 SOC 估算方法，其原理是预先知道上一时刻电池剩余电量状态，并对一段时间内电池充入、放出的电荷量进行统计，从而得到当前电荷状态的一种方法。但是，由于此方法对电池剩余电量状态较为依赖，并且由于电流传感器精度不足，信号受干扰等原因，统计电荷量时会产生误差，而且误差会随着时间不断累积。

本文中，我们使用改进后的电荷累积法–开路电压法作为均衡依据。首先，通过恒流充放电实验测出开路电压UOCV与 SOC 的关系曲线，推导出开路电压的预估公式，用电池停止放电后某一时刻的电压预估电池的开路电压，从而缩短获得开路电压的静置时间；然后，在充放电时利用电荷累积法估算电池 SOC，在电池静止时利用开路电压法对SOC 值进行修正，弥补电荷累积法误差不断累积的缺陷[8]。

3.2 电池分级

为了在均衡前选择适合的均衡方法，应该在电池使用阶段对各单体电池的剩余电量分布情况进行实时监控，因此我们引入了对单体电池分级的构想。首先，依据电池组剩余电量的平均值将单体电池分为 2 个等级；然后，根据设定阈值将电池组中的单体电池分为 4 个等级，其中x1代表二级高的单体电池数量，x2代表一级高单体电池数量，以此类推（见图 3）。按图 4 所示电池分级流程图，以4 节单体锂电池组成的电池组为例阐述分级方法：首先，监测电池的剩余电量，根据单体电池的 SOC值将电池由大至小进行初始排序；其次，计算电池组的平均 SOC 值，记作ηavg；再次，根据各单体电池 SOC 值与ηavg的差值对电池进行一次分级，记为集合D（其中，+ 代表大于平均值，- 代表低于平均值），例如D=｛+2 %, +1 %, -1 % , -2 %｝代表第 1 只电池的剩余电量比平均剩余电量高 2 %，第 2 只电池的剩余电量比平均剩余电量高 1 %，同理可得出后两只单体电池的情况；然后，再次根据电池的容量情况对电池的电荷量进行二次分级，按照剩余电量由高至低，将单体电池共划分为 4 个等级（二级高、一级高、一级低、二级低）。

图3 电池分级规则

图4 电池分级流程

若D＞ 0 且＞z %，则认定为二级高，若D＞ 0且＜ z %，则认定为一级高；若D＜ 0 且＞ -z%，则认定为一级低，若D＜ 0 且＜ -z%，则认定为二级低。其中，z的值可以根据用电设备的要求进行确定。通过这种分类方式，不但能够根据平均值对电池剩余的电量进行高低划分，而且还能够获得电池剩余电量相对于平均值的高低程度，使我们能更好地了解电池剩余电量的分布情况，以便于后期根据不同的情况对电池组进行均衡。通过上述的分类方法，我们得到了一个关于电池剩余电量分布情况的向量B，例如B=（x1,x2,x3,x4），其中x1为二级高单体电池的数量，x2为一级高单体电池的数量，以此类推，并且x1+x2+x3+x4等于电池组中单体电池的数量。

3.3 电池均衡

根据向量B的情况选择不同的均衡电量和目标电池，按图 5 所示流程进行均衡。均衡原则为：每次均衡的电荷量为不均衡电池剩余电量相距平均值一半的电荷量，即随后通过对电池的分布情况重新进行分级、均衡、不断迭代，直至完成均衡。

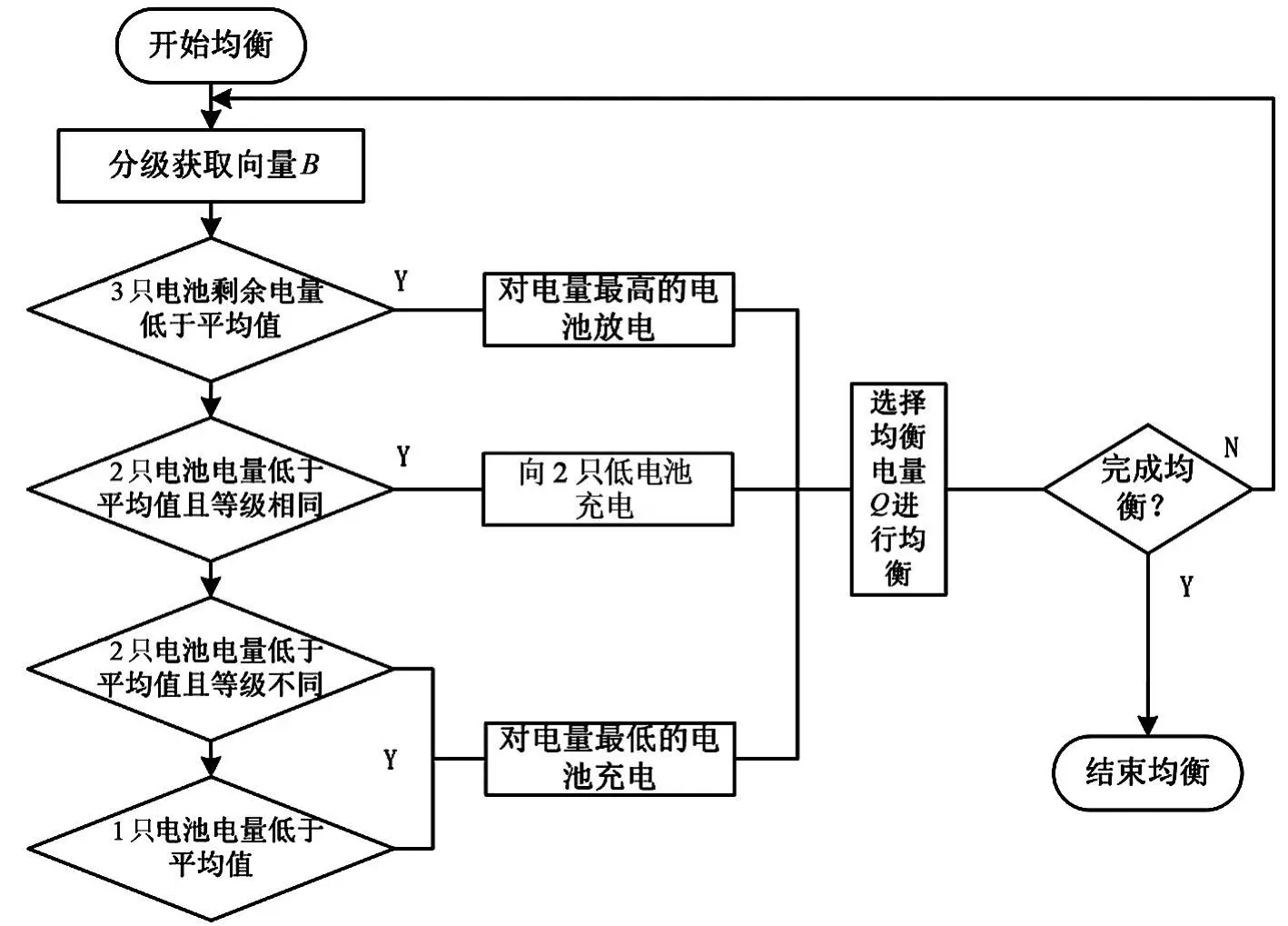
图5 均衡策略流程图

为了更好地阐述不同情况下的能量转移方法，方便编写仿真程序，首先以 4 只单体电池组成的电池组为例观察向量B中x3和x4的情况，则有（x,x, 3, 0）、（x,x, 0, 3）、（x,x, 2, 1）、（x,x, 1,2）、（x,x, 2, 0）、（x,x, 0, 2）、（x,x, 1, 1）、（x,x, 1, 0）、（x,x, 0, 1）共 9 种情况，根据低电量电池分布情况，可将上述 9 种情况分为以下 4 种均衡方法。

第 1 种：当 3 只电池剩余电量低于平均值时，向量B的情况包括（x,x, 3, 0）、（x,x, 0, 3）、（x,x, 2, 1）、（x,x, 1, 2），可等同于（1, 0,x,x），则通过剩余电量高的电池向整组电池进行能量转移的方法能够更高效地使电池组达到最佳状态，在这里，均衡量取高剩余电量与平均值差值的一半，最终二级高电池减少的电量为

其中，Dn(1,1) 为第n次均衡时第 1 只电池剩余电量与平均值的差值，m为电池组中单体电池的数量。

第 2 种：当 2 只电池的剩余电量低于平均值且等级相同时，向量B包括（x,x, 2, 0）或（x,x, 0,2），说明有两只剩余电量低于平均值的电池，而且这两只电池剩余电量的差距不太大，所以通过整个电池组向 2 只低剩余电量电池同时进行能量转移能够更快地达到均衡的目的。2 只低电池获得的电量为

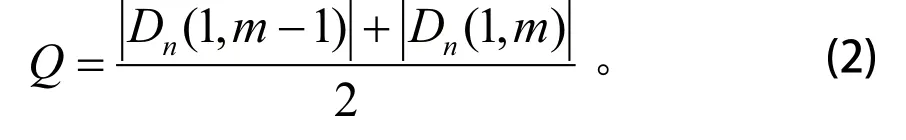
第 3 种：当 2 只电池的剩余电量低于平均值且等级不同时，向量B为（x,x, 1, 1），则向二级低的电池进行能量转移，直至它的剩余电量与一级低电池的相等。二级低电池获得的电量为

第 4 种：当只有 1 只电池的剩余电量低于平均值时，向量B包括（x,x, 1, 0）或（x,x, 0, 1），则通过整个电池组向低电量的电池进行充电。低剩余电量电池获得的电量为

此方法可以根据电池的实时状态，改变均衡的方法，使低电量电池的剩余电量无限接近平均值。若电池组中单体电池数量增加至m，只需遵守均衡原则修改上述 4 种情况即可。

4 均衡实验

采用由 4 只 1200 mAh 聚合物锂电池串联组成的电池组作为实验对象，采用的充电设备为艾德克斯公司生产的 IT6942A 电源，放电设备为IT8512C+ 的电子负载。利用实验得到开路电压与SOC 的对应表，便于电池停止工作时消除电荷累积法对误差的累积，并利用 Matlab 对均衡策略进行验证。

4.1 SOC 估算

首先根据以下 2 个步骤对充满电的电池进行循环放电：① 用 1C放电倍率对电池放电达时间t；② 断开负载进行静置，直至电池电压稳定时记录电压值。根据公式

计算出t时段内电池放出的电荷量。其中：Qd为放出的电荷量；d为循环放电次数；Id为放电电流；t为放电时间。重复步骤①②，直到电池达到放电截止电压。

在上面的实验中，我们得到了一组开路电压与一组电荷量的值，将每个放电时间段的电荷量相加，就可得到电池的总容量。根据公式

计算放出电荷量Q1后的 SOC 值ηSOC。同样，可以得到放出的电荷量Q2，Q3……Qd对应的 SOC 值，与开路电压一一对应后得到开路电压UOCV与ηSOC的对应曲线（见图 6）。然后，通过实验得到不同放电倍率下的回弹曲线（见图 7），并拟合出开路电压估算公式。在电池静止时，利用开路电压法对SOC 值进行修正，开路电压与 SOC 对应关系如表2 所示，充放电时利用电荷累积法估算电池 SOC。

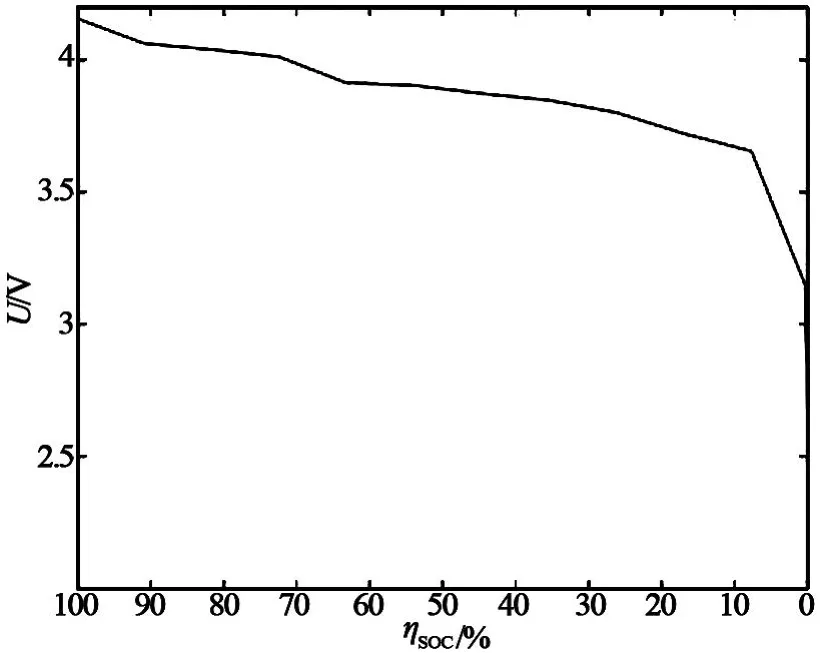
图6 开路电压与 SOC 对应关系

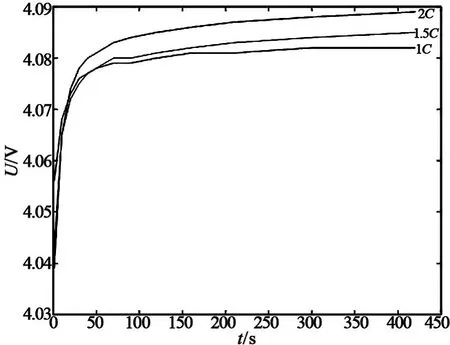
图7 电压回弹曲线

表2 开路电压与 SOC 对应关系

4.2 均衡系统仿真

使用 Matlab 作为仿真工具，编写 M 文件对上述均衡策略进行仿真。假设 4 只单体电池的 SOC值ηSOC分别为 55 %、52 %、51 %、60 %，那么通过上述方法均衡后的结果如图 8 所示。首先，依据剩余电量对单体电池从大到小重新排序；其次，计算平均值ηavg= 0.545，对电池进行分级，结果为（2,0, 0, 2），说明有 2 个二级高和 2 个二级低的电池；接着，根据第 2 种均衡策略，进行第一步均衡后各电池的容量分布分别为 58.5 %、53.5 %、53.49 %、54.5 %，再次对电池进行分级，结果为（1, 0, 2, 1）；然后，根据第 1 种均衡策略，第 2 次对电池组进行均衡，均衡结果为 56.5 %、54.17 %、54.16 %、53.16 %；最后，经过 3 次均衡后，得到的分级结果为（0, 3, 1, 0），为 3 个一级高和 1 个一级低。ηSOC,max与ηSOC,min的差距控制在 1 % 之间。具体的仿真数据如表 3 所示。

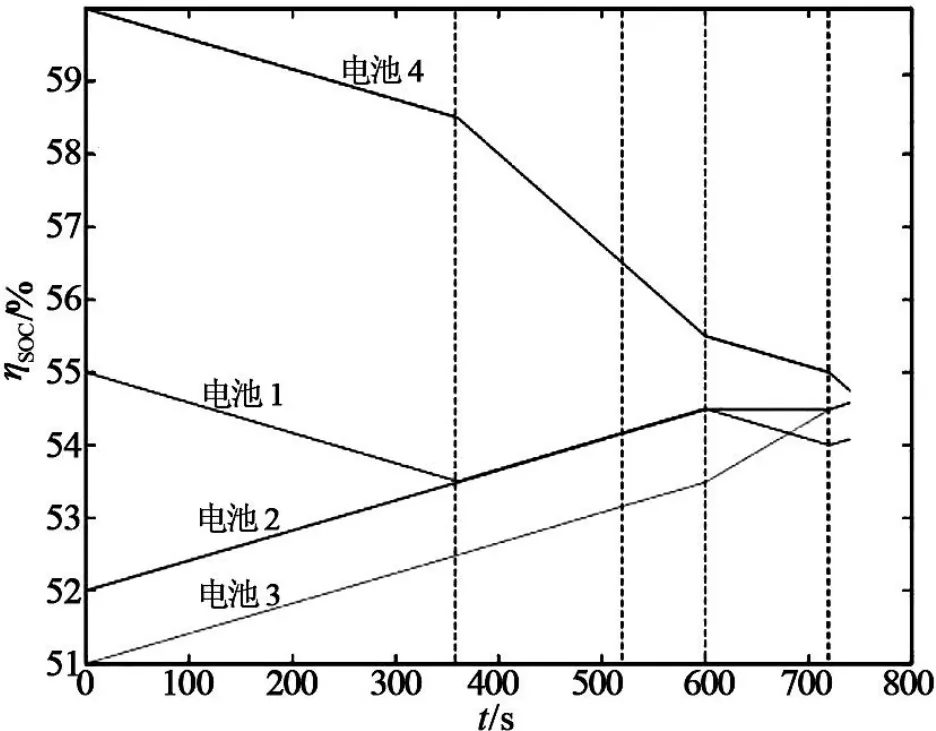
图8 均衡结果

表3 基于剩余电量分级均衡结果

通过图 8 及表 3 可以表明，此均衡方法在第 4次均衡后就可以将电池组中单体电池的 SOC 值差距保持在 1 % 内。除了电池 2 由于 SOC 值比较接近平均值，会出现少量反复充电之外，其他 3 只电池的剩余电量都是无限靠近平均剩余电量，减少了对电池反复充放电次数。与文献 [6]中的均衡策略相比，具有均衡次数少，能量损耗小等特点。