基于Verilog-A 语言的霍尔元件仿真模型的建立

伍凤娟，刘树林，杨 波

0 引言

传感器技术是现代信息技术的3大支柱产业之一，如今已步入高速发展的阶段。霍尔传感器由于结构简单、成本低廉等特点在整个传感器家族中起着举足轻重的作用，被广泛应用于工业控制、智能仪表、消费电子、现代医疗等领域［1］。霍尔传感器是一种基于霍尔效应的器件，能实现磁电转换，可以直接测量磁场大小，也可以间接测量一些非磁量，如速度、角度、位置、压力、电流等。例如:可用于无触点开关、无刷直流电机、汽车速度表和里程表、ABS系统中的速度传感器以及导航系统等。霍尔元件是霍尔传感器的重要组成部分［2］，对霍尔元件进行仿真模型的建立可以有效提高仿真精度，从而促进霍尔集成电路的发展。

霍尔元件自诞生以来就被广泛研究，尤其是对霍尔元件模型的建立与分析更是备受业内研究者的青睐。霍尔元件的模型大致有以下几种:①四电阻wheatstone电桥模型。该模型结构简单，是最早的霍尔元件仿真模型［3］，但该模型没有综合考虑非线性电阻、几何因素、温度漂移、频率响应、封装应力等物理效应的影响，仿真精度低，不能满足霍尔传感器精度需求;②一种基本单元数量可缩比的精确仿真模型［4］。该模型由Dimitropoulos等人于2007年提出，其基本单元由结型场效应晶体管和电流控制电流源组成，其单元数量可根据仿真精度要求灵活改变。通过增加基本单元数量来提高仿真精度，但牺牲了仿真速度，同时该模型不适用于CMOS十字形水平霍尔元件。该模型能够保证精度，却不能应用于EDA工具，如Pspice，故其应用范围受到极大限制;③等效集总电阻模型［5］。该模型采用有限元分析法来分析有源区电阻非对称性产生的失调，通过非线性失调分量来模拟由偏置电压改变而造成的结场效应大小的变化。该模型虽然能够模拟霍尔元件失调电压，但不能模拟磁场灵敏度，也不能直接在电路仿真器上运行。虽然最近又提出了一个非线性电阻模型，但模型结构复杂，功能也不完整［6］。

对上述霍尔元件各模型特点及方法进行对比后，考虑到实际应用情况，本文采用8个电阻、4个反偏二极管、4个电流控制电压源和4个JFET来模拟霍尔元件的等效模型。其中，八电阻网络可以更好地反映电流流动，4个反偏二极管用来表示霍尔元件工作时的寄生效应、4个电流控制电压源用来模拟磁场和霍尔电压的关系［7］、4个JFET可以有效提高霍尔元件的交流特性。该模型充分考虑了非线性、几何因子及温度效应等因素，电路结构简单、精度高。

1 Verilog-A语言简介

Verilog-A是一种硬件描述语言，它具有高层次、模块化的特点，可用于描述模拟系统和它子系统的结构及行为，也可以用来描述一些比较传统的系统，像流体力学系统、固体力学系统和热力学系统等［8］。采用Verilog-A语言描述硬件电路有两种方式:结构描述和行为描述。结构描述实际上是对整个系统结构框图的描述，它主要描述的是系统中各个子模块的用途及子模块之间的连接关系，为了实现完整的结构描述，必须要先定义信号、端口以及一些基本参数。行为描述主要采用一些传输函数和数学表达式来描述目标电路，不仅可以描述电阻、电感、电容等一些简单的元件，还可以描述一些非常复杂的模拟系统，如滤波器、高速D/A转换器等，描述范围极其广泛。采用Verilog-A语言描述的模块可以用 Cadence中的Spectre仿真器对其进行仿真，还可以通过分析仿真结果对电路参数进行调整。由于行为描述无须考虑到晶体管级，只需描述清楚输入与输出之间的关系［9］，因此，仿真时所需时间短、精度高。

2 霍尔元件设计与工艺分析

2.1 霍尔元件

霍尔元件为一四端器件，其主要参数有:输入、输出电阻、霍尔系数、霍尔灵敏度等。常用的霍尔元件材料有:N-Ge，N-Si，GaAs，InSb，InAs 和InAsP．其中，InSb，InAs和 InAsP的迁移率高、霍尔元件灵敏度高，但这几种材料电阻率很小，因此霍尔系数较小。N-Ge，N-Si和GaAs的霍尔系数较大［10］，是比较常见的制作霍尔元件的材料，由于GaAs的禁带宽度和迁移率大，在器件性能上要比N-Ge和N-Si的性能好，但其价格也最高。而Si材料的温度特性好、性价比高，应用更为广泛。

在对霍尔电压进行研究时，假设霍尔元件是理想的，也就是说器件的电极接触点无限小、长宽比L/W趋于无穷大，整个霍尔元件近似于一个半导体薄片。但由于种种原因，实际的霍尔元件尺寸是有限的，霍尔电压VH不仅与器件的几何参数W/L有关，还和器件的几何修正因子G(geometrical correction factor)有关［11］。考虑到几何修正因子G，其霍尔电压表达式为

式中 VH为霍尔电压，mV;G为几何修正因子(其范围为0～1);μn为载流子迁移率，cm2/V·s;W/L为霍尔元件的宽长比;V为霍尔元件两端施加的电压，V;B为磁感应强度，T．

2.2 霍尔元件工艺分析

在集成电路中，隔离方式的不同是区别霍尔元件和分立元件的一个标准。分立霍尔元件采用的是空气和其他绝缘介质与电子器件相互隔离的，而集成电路中的霍尔元件是采用标准双极工艺中的PN结隔离［12］。

在P-SUB上制作 N-epi，N-epi用于制作霍尔元件。在双极工艺过程中，同时形成了霍尔电极的N+接触和NPN晶体管的发射极。N-epi之上要覆盖一层浅掺杂的P+注入，这层P+注入层可有效减小霍尔元件的厚度，在一定程度上提高霍尔灵敏度。另一方面，P+注入层在N-epi和SiO2之间形成了一个静电屏蔽层［13］，这可以降低表面效应对霍尔元件的影响，从而提高可靠性。芯片表面要覆盖一层SiO2，并淀积一层Si3N4，N-epi周围的PN结起隔离作用。在一定的温度范围内，只要PN结处于反偏状态，霍尔元件就可以正常工作。在霍尔元件的周边要有足够的P型隔离环，从而保证相邻电路不受霍尔信号的干扰［14］。双极型霍尔元件的版图如图1所示。

图1 双极型霍尔元件的版图Fig．1 Layout of the bipolar hall element

图2 所示为双极型霍尔元件的剖面图。霍尔元件在恒压模式下工作时迁移率是受工艺因素影响的唯一参数，在集成电路工艺中，外延层浓度为1015～1016之间［15］，在此浓度范围内迁移率几乎不受杂质浓度的影响。而对于CMOS工艺而言，在P-SUB上形成低掺杂的N-well，霍尔元件直接制作在N-well中，再将一层浅掺杂的P+层覆盖在N-well上，最后在作为霍尔元件输入、输出端口的N-well的4个顶角位置进行N+注入。由于N-well的掺杂浓度比较高，而磁场的灵敏度和N-well的掺杂浓度成反比，所以，CMOS集成霍尔元件的磁场灵敏度比双极工艺的磁场灵敏度低。此外，CMOS集成霍尔元件对工艺波动、温度漂移以及机械压力等因素比较敏感，会产生严重的失调和低频噪声［16］。因此，采用双极工艺来实现。

图2 双极型霍尔元件的剖面图Fig．2 Cross-section of the bipolar hall element

3 霍尔元件模型及Verilog-A语言实现

霍尔元件仿真模型如图3所示。

图3 霍尔元件仿真模型图Fig．3 Simulation model of the hall element

根据霍尔元件的90°对称特性及范德堡法［17］测量体电阻，可得

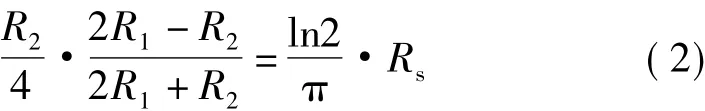
霍尔元件中心部分相对应的节点之间的电阻可表示为

由式(2)、(3)可得，霍尔元件电路模型的电阻R1和R2可分别表示为

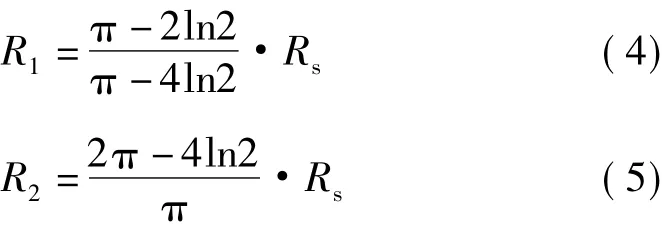
对于一般霍尔元件，其方块电阻为

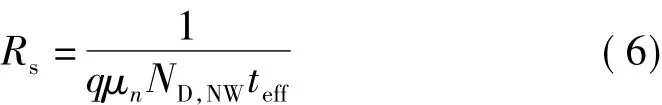
式中 q为电荷量，C;μn为电子迁移率，cm2/V·s;ND，NW为 N型外延层掺杂浓度，cm－3;teff为N型外延层有效厚度，μm．由图2知:teff=tNW－tP+－ wNW，SUB－wNW，P+，其中，tNW为 N 型外延层的厚度 μm;tP+为顶部 P+ 层的厚度，μm;wNW，SUB，wNW，P+分别为2个PN结耗尽层的厚度，μm．

式中 NA，SUB为 P 型衬底的掺杂浓度，cm－3;εsi为Si的介电常数;NA，P+为顶部 P+层掺杂浓度，cm－3;Upn为反偏 PN 结电压，V;Vbi，P+和 Vbi，SUB为PN 结自建电势，V，其值分别为耗尽区的厚度会受反偏PN结电压Upn的调制作用［18］，因此电阻呈现出非线性效应。

由于顶部P+层的掺杂浓度明显高于P-SUB的浓度，因此，顶部耗尽区的厚度变化受反偏电压的影响可以忽略不计。将式(6)泰勒展开得

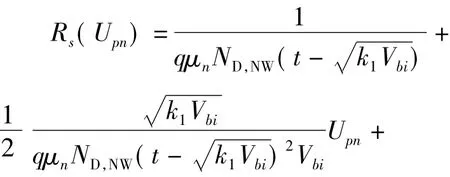
由于半导体材料对温度具有很强的依赖性，因此温度漂移会对等效电阻、霍尔元件的灵敏度和失调电压产生一定的影响。导带中载流子数目会随着温度的升高而增多，因此，由N外延层所构成的霍尔元件的电阻阻值会增大，进而使得流过霍尔元件的电流减小，最终使霍尔电压减小。考虑温度系数后，电阻的表达式变为

式中 RTC1，RTC2分别为电阻的一阶、二阶温度系数，%/℃，ppm/℃，其值由工艺文件提供;T为开尔文温度，K．

在对霍尔元件进行模型建立时，除过考虑电阻影响外，灵敏度也是一个非常重要的参数。考虑几何校正因子G，电流相关灵敏度［19］为

式中 μH为霍尔迁移率，cm2/V·s，且Si和Sv可通过下式互相转换

式中 rin为2个输入端口之间的等效电阻，Ω;N为输入端口之间对应的扩散电阻的方块数，由霍尔元件的L和W决定。

考虑温度变化的影响，电流相关灵敏度可进一步写成

式中 BBS1，BBS2分别为一阶、二阶电流相关灵敏度系数，%/V，%/V2，由相关工艺文件提供。

该霍尔元件工艺模型参数见表1．

表1 模型中相关物理参数Tab．1 Physical parameters for the model

该霍尔元件等效模型的Verilog-A语言的主要描述语句如下

V0=abs(V(left，right));

V1=(k0*V0*V0+sqrt(k0*k0*V0*V0*V0+4*k2*k0*fi0*V0*V0*(fi2+V0)))/2/k2/(fi2+V0);

w0=sqrt(k0*(fi0+V1));

w2=sqrt(k2*(fi2+V0));

w3=sqrt(k3*fi3);

c1=`P_EPS0*er*(4*l+w)*w/4/w3;

c2=`P_EPS0*er*(4*l+w)*w/w0;

rsv=1/(`P_Q*u*nd*(t－tp－w3－w2+w0));

rst=rsv*(1+rtc1*(S|temperature－T0)+rtc2*(S|temperature－T0)*(S|temperature－T0));

rd=2*rst*('M_PI*(1/w+1/3)－ln(2))*(1/w+1/3)/('M_PI*(1/w+1/3)－2*ln(2));

rh=4*rst*('M_PI*(1/w+1/3)－ln(2))/'M_PI;

G=0．47;

siv=G*uh*rsv;

sit=siv*(1+ts1*(S|temperature－T0)+ts2*(S|temperature－T0)*(S|temperature－T0));

V(ti，x) ＜ +I(ti，x)*rd;

V(bi，x) ＜ +I(bi，x)*rd;

V(li，x) ＜ +I(li，x)*rd;

V(ri，x) ＜ +I(ri，x)*rd;

V(ti，li) ＜ +I(ti，li)*rh;

V(li，bi) ＜ +I(li，bi)*rh;

V(bi，ri) ＜ +I(bi，ri)*rh;

V(ri，ti) ＜ +I(ri，ti)*rh;

I(top，sub) ＜ +ddt(V(top，sub)*c1);

I(bottom，sub)＜ +ddt(V(bottom，sub)*c1);

I(left，sub) ＜ +ddt(V(left，sub)*c1);

I(right，sub) ＜ +ddt(V(right，sub)*c1);

I(x，sub) ＜ +ddt(V(x，sub)*c2);

V(ti，ti2) ＜ +0．0;

V(ri，ri2) ＜ +0．0;

V(bi，bi2) ＜ +0．0;

V(li，li2) ＜ +0．0;

It=I(ti，ti2);

Ib=I(bi，bi2);

Ir=I(ri，ri2);

Il=I(li，li2);

V(right，ri2) ＜ +0．5*(sit－ m0*Ib)*Ib*V(fld);

V(top，ti2) ＜ +0．5*(sit－ m0*Ir)*Ir*V(fld);

V(left，li2) ＜ +0．5*(sit－ m0*It)*It*V(fld);

V(bottom，bi2) ＜ +0．5*(sit－m0*Il)*Il*V(fld);

end

endmodule

图4所示为在输入电压3．3 V下，当磁场强度从1 mT增加到10 mT时，霍尔元件的模型仿真与同一工艺条件下理论计算的结果比较图。从图中可以看出磁场强度与霍尔电压的对应关系，同时表明所建立的霍尔元件模型的正确性。

图5为薄层电阻与偏置电压仿真结果与理论测量对比图。在室温下，当外部输入偏压从0 V变化到5 V时，得到的薄层电阻随偏压的关系。从图中可以看出，薄层电阻模型仿真结果与理论计算偏差较小，达到了实际应用要求。

由于温度对模型的精度影响很大，在无封装应力的前提下，当温度从－40℃增加到120℃时，电流相关灵敏度随温度变化的仿真结果如图6所示。在－40℃到120℃范围内，其模型仿真结果与实际测试结果达到了很好的一致性。

图4 模型仿真与理论计算在3．3 V输入电压下的结果比较Fig．4 Comparisons between the model simulation and the theoretical calculation under 3．3 V input voltage

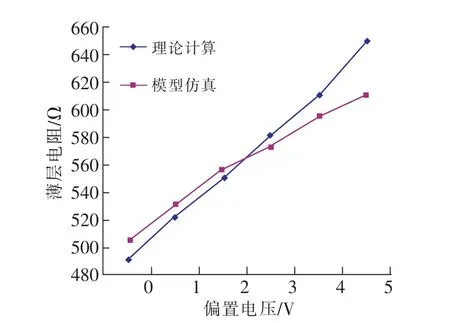
图5 薄层电阻与偏置电压仿真与理论测量对比Fig．5 Comparisons between the simulation and measurement of the sheet resistance versus bias voltage

图6 电流相关灵敏度随温度变化的仿真与测试比对Fig．6 Comparisons between the simulated and measured relative variation of the current related sensitivity versus temperature

采用Cadence Spectre仿真器对上述电路模型进行仿真，得到电源电压为3．3 V时的仿真结果，如图7所示。结果显示霍尔元件产生的是一对大小相等、方向相反的互补信号。由式(1)所示的霍尔电压表达式可知:取最大值 0．47，μn为1 200 cm2/V·s，偏置电压为3．3 V，取不同的磁场值并将这些参数代入式(1)中即可得到霍尔电压的具体值。

图7 霍尔电压仿真结果Fig．7 Simulation results of the hall voltage

4 结论

1)该模型由8个电阻、4个反偏二极管、4个电流控制电压源和4个JFET组成。该模型结构简单，考虑了霍尔元件几种重要的物理效应，如:温度效应、几何效应、非线性电阻及寄生效应等;

2)采用硬件描述语言Verilog-A实现，非常易于在通用cadence spectre仿真器上对霍尔元件及整个霍尔电路进行仿真分析，可操行性强;

3)通过实际测试表明:该模型的仿真结果与相同工艺条件下霍尔元件的测试结果达到了很好的一致性，显示出该模型具有较高的仿真精度及仿真速度，且该模型的建立有助于提高霍尔集成电路设计的可靠性;

4)不足之处在于:该模型没有考虑磁阻效应的影响，且不能用于垂直型霍尔元件，通用性不强。未来需对各类霍尔元件内部结构及物理效应进行深入研究，探索简单、实用、精确的仿真模型，进一步提高霍尔传感器的仿真精度。

［1］ 徐 跃．高灵敏度的CMOS霍尔磁场传感器芯片设计［J］．仪表技术与传感器，2009(12):14－16．XU Yue．Design of high sensitive CMOS monolithic magnetic hall sensor［J］．Instrument Technique and Sensor，2009(12):14 －16．

［2］ 何秋阳，徐 跃，赵菲菲．十字型CMOS集成霍尔传感器的简化仿真模型［J］．仪表技术与传感器，2011(10):13－15．HE Qiu-yang，XU Yue，ZHAO Fei-fei．Simplified simulation model for cross-shaped CMOSintegrated hall sen-sor［J］．Instrument Technique and Sensor，2011(10):13－15．

［3］ 黄海云．CMOS单片集成3D霍尔磁传感器研究与设计［D］．大连:大连理工大学，2016．HUANG Hai-yun．Research and design of CMOSmonolithic integrated 3D hall magnetic sensor［D］．Dalian:Dalian University of Technology，2016．

［4］ 朱振铎．高灵敏度片上水平霍尔传感器［D］．南京:南京大学，2015．ZHU Zhen-duo．A high sensitivity on-chip horizontal hall sensor［D］．Nangjing:Nangjing University，2015．

［5］ 张 浩．霍尔集成电路设计及其测试系统的研发［D］．兰州:兰州大学，2010．ZHAGN Hao．The design of hall ICand the R＆D of hall sensor testing apparatus［D］．Lanzhou:Lanzhou University，2010．

［6］ Dimitrov K．3 － D silicon hall sensor for use in magnetic-based navigation systems for endovascular interventions［J］．Measurement，2007，40:816 － 822．

［7］ Xu Y，Zhao F F．A simplified simulation model for CMOS integrated Hall devices working atlow magnetic field circumstance［C］//In Proceedings of the 10th IEEE International Conference on Solid-State and Integrated Circuit Technology(ICSICT)，Shanghai，2010:1925－1927．

［8］ Xu Y，Pan H B．An improved equivalent simulation model for CMOS integrated hall plates［J］．Sensors，2011，11(6):6284 －6296．

［9］ 杨 波，杨银堂，孙龙杰，等．基于Verilog-A的容栅传感器建模与仿真［J］．电子器件，2005(4):871－874．YANG Bo，YANG Yin-tang，SUN Long-jie，et al．Modeling and simulation of capacitive gate transducer using Verilog-A［J］．Chinese Journal of Electron Devices，2005(4):871－874．

［10］ Vasyukov D A，Plaut A S，Henini M，et al．Intrinsic photoinduced anomalous Hall effect［J］．Physica E，Low-dimensional Systems and Nanostructures，2010，42(4):940－943．

［11］ Morgan Madec．An improved compact model of the electrical behaviour of the 5-contact vertical Hall-effect device［J］．Analog Integr Circ Sig Process，2014，81:677－691．

［12］徐 俊．一种低失调垂直型霍尔传感器研究与设计［D］．南京:南京邮电大学，2017．XU Jun．Research and design of a low offset vertical hall sensor［D］．Nanjing:Nanjing University of Posts and Telecommunications，2017．

［13］ Schell JB．Hall-effect magnetic tracking device for Magnetic Resonance Imaging［C］//In IEEE Sensors Conference．Baltimore，USA．doi:10．1109/ICSENS．2013．6688475，2012:1382 －1385．

［14］吕 飞．单芯片CMOS三维微型霍尔磁传感器研究［D］．南京:南京大学，2017．LV Fei．Research on single-chip integrated CMOS 3D micro hall magnetic sensor［D］．Nanjing:Nanjing University，2017．

［12］徐 跃，黄海云．一种十字形CMOS霍尔器件的精确仿真模型［J］．功能材料与器件学报，2014，20(1):20－26．XU Yue，HUANG Hai-yun．An accurate simulation model for cross-shaped CMOS Hall sensor［J］．Journal of Functional Materials And Devices，2014，20(1):20－26．

［16］ Madec M，Kammerer JB，Hebrard L，et al．An improved compact model for CMOS cross-shaped Hall-effect sensor including offset and temperature effects［J］．Analog Integr Circ Sig Process，2012，73:719 －730．

［17］ Banjevic M，FurreR B，Blagojevic M．，et al．High-speed CMOSmagnetic angle sensor based on miniaturized circular vertical Hall devices［J］．Sens．Actuators，2012，178:64－75．

［18］ Chang T，Kai-Cheung Juang．CMOS SC-spinning，current-feedback Hall sensor for high speed and low cost applications［C］//In:Proc．of IEEE Sensors conference，2014:527 －530．

［19］ YUE Hu，WEN Rong-yang．CMOSHall sensor using dynamic quadrature offset cancellation［C］//In:Solid-State and Integrated Circuilt Technology，2006:284－286．