基于匹配追踪法的信号分解方法研究

王猛 张若伟 尹扬帆

摘要：目前基于希尔伯特-黄变换理论的信号分解方法都是按照信号频率由高到低进行分解，在分解过程中，不可避免地会出现能量的混叠和频率的交叠。基于匹配追踪法的信号分解方法研究的主要内容是提出一种基于匹配追踪法的信号自适应分解和分层的方法，将信号分解重构为重建信号与残差信号，对分解出的分量求解瞬时频率和瞬时振幅等参数。通过仿真实验可以看出，该方法在信号时频分析中是具有可行性的。

关键词：匹配追踪法;重建信号;瞬时频率;仿真实验

中图分类号：TP3        文献标识码：A        文章编号：1009-3044（2018）36-0240-02

1 概述

我们所生活的现实物理世界中，接触的信号大多是非平稳随机信号[1]。信号分解的质量直接决定时频分析的结果，因此对非平稳随机信号分解算法的改进一直是研究热点。

1998年，美籍华人Norden E.Huang等提出了一种新的时频分析方法——希尔伯特-黄变换[2]，首次针对瞬时频率的悖论，以使信号的瞬时频率值具有明确的物理意义为宗旨，提出了将多分量信号分解成单分量信号的思想和方法，从而打破了傅里叶变换的传统思想，形成了一种非常适合分析非线性、非平稳信号的具有自适应能力的新方法[3，4]，带来了信号时频分析领域的新局面。

希尔伯特-黄变换首先对信号进行经验模态分解，产生一系列具有不同特征尺度的固有模态函数，再对每一个固有模态函数进行希尔伯特变换，进而得到能量在时间和频率上的分布规律[5]。但是经验模态分解过程中IMF分量之间的正交性是通过筛分迭代算法近似实现的，还没有得到彻底的解决方案和完整的理论解释，从而不可避免的导致能量的混叠和频率的交叠[6]。

2006 年，压缩感知的概念被正式提出，压缩感知原理是将信号投影到给定域上，感知到一组压缩数据，利用最优化的方法实现对压缩数据解密，估计出原始信号的重要信息[7，8]，该方法最大的优势是突破了香农采样定理的瓶颈[9]， 使得高分辨率信号的低采样率采集成为可能[10，11]。通过信号在过完备库上的分解，用来表示信号的基可以自适应的根据信号本身的特点灵活选取，分解的结果将会是信号的一个特别简洁的稀疏表示[12]。

因此，从理论上说，该方法对复杂信号进行分解不但是可行的，也是目前最好的方法。通过对信号的稀疏字典的设计，灵活的选择与信号局部特征最为匹配的原子，以精确地逼近信号结构，可以达到我们层层分解原始信号的目的;將分解出来分量，分别进行时频分析，可以求得我们所需要的信号具体参数。

2 基于匹配追踪法的信号分解

基于匹配追踪法的信号分解方法中，匹配追踪（matching pursuit）属于贪婪算法，并不是最优化算法[13，14]，它不像凸优化算法那样有一个目标函数并使之最小，而是通过一次次的迭代找到待重建k稀疏信号x的非零元素的位置及幅度，从而实现对x的恢复[15]。其具体分解过程如下：

（1） 给出输入信号[x（t）]，设置迭代次数，通常情况下，迭代次数越高，分解越精确，但是同时所花时间也越长。将重建信号初始化置零。

（2） 设置原子库索引参数。

（3） 开始迭代，让原始信号在最佳原子上投影（使投影值极大化），然后迭代，不断地将剩余量再投影在最佳原子上，使剩余量最小化。贪婪选择过程即为选取与信号内积最大的子波，即振幅最大值。

（4） 输出重建信号和残差信号。通常情况下，重建信号为原输入信号中的低频分量，残差信号为原输入信号中的高频分量。

3 实验仿真与结果分析

3.1 实验仿真

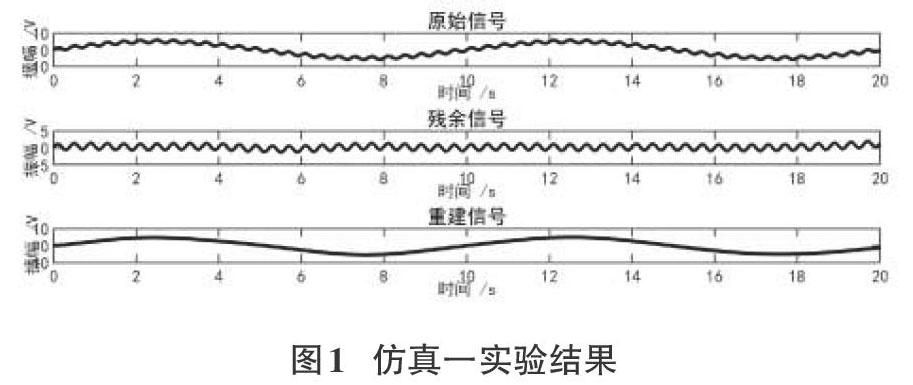
仿真一采用两个正弦信号叠加，原始信号sig=5*sin（0.2*pi*t）+1*sin（5*pi*t）;迭代次数设置为5次，字典库子波采用ricker子波，实验结果如图1所示。

3.2 结果分析

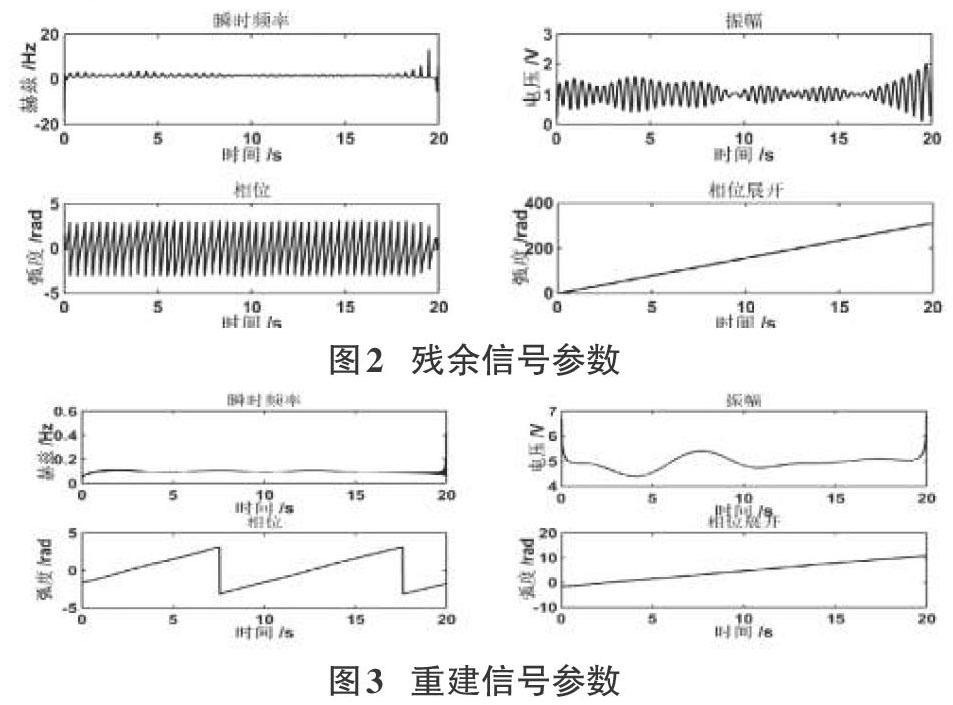
从实验仿真结果可以看出，无论是正弦叠加的信号、含有高斯噪声的信号，还是形态有明显差别的信号，此方法都可以很好地进行信号的分解。信号分量的整体趋势不会发生变化，通过希尔伯特变换，可以计算出符合信号原始特征的瞬时频率等参数。

虽然基于匹配追踪法的信号分解方法能够对信号进行很好的分解，但是针对某些信号，不难看出，在信号整体时间区间内依旧出现了计算出了负频率。若出现在端点处，可以通过周期延拓方式解决;若出现在时间区间中段，则可以通过改变子波种类，提升字典性能解决。

4 总结与展望

基于匹配追踪法的信号分解方法能够较好地实现信号的分解，分解出的信号通过希尔伯特变换能够计算出瞬时频率等参数。由于采用的字典库能够根据需要分解的信号类型，人工调整原子种类，且自由调节相关参数，所以具有很强的自适应性和可操作性。除用MP算法外，采用OMP算法，K-SVD法等均可实现信号的分解重构，且具有良好性能，在今后的研究中，可以采用诸如此类的方法，不断对时频分析方法进行补充与完善。

参考文献：

[1] 胡广书. 现代信号处理教程[M]. 清华大学出版社， 2015.

[2] Huang N E， Wu Z. A review on Hilbert-Huang transform： Method and its applications to geophysical studies[J]. Reviews of Geophysics， 2008， 46（2）.

[3] Huang N E， Shen Z， Long S R， et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering Sciences， 1998， 454（1971）：903-995.

[4] 安怀志. 希尔伯特黄变换理论和应用的研究[D]. 哈尔滨工程大学， 2008.

[5] 钟佑明， 秦树人. 希尔伯特-黄变换的统一理论依据研究[J]. 振动与冲击， 2006， 25（3）：40-43.

[6] 胡爱军， 孙敬敬， 向玲. 经验模态分解中的模态混叠问题[J]. 振动.测试与诊断， 2011， 31（4）：429-434.

[7] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory， 2006， 52（4）：1289-1306.

[8] Kutyniok G. Compressed Sensing： Theory and Applications[J]. Corr， 2012， 52（4）：1289 - 1306.

[9] 李树涛， 魏丹. 压缩传感综述[J]. 自动化学报， 2009， 35（11）：1369-1377.

[10] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory， 2006， 52（4）：1289-1306.

[11] 李卓凡， 閆敬文. 压缩感知及应用[M]. 国防工业出版社， 2015.

[12] Lustig M， Donoho D J. Sparse MRI： The application of compressed sensing for rapid MR imaging[J]. Journal of the Chemical Fertilizer Industry， 2010， 58（6）：1182-1195.

[13] Mallat S G， Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Trans on Signal Processing， 1993， 41（12）：3397-3415.

[14] 闫敬文， 刘蕾， 屈小波. 压缩感知及应用[M]. 国防工业出版社， 2015.

[15] Mallat S， Zhang Z. Matching pursuit with time-frequency dictionary[J]. IEEE Transactions on Signal Processing， 1993， 41（12）：3397-3415.

[通联编辑：代影]