基于多分类问题处理机制的研究
2018-03-04李浩舒炫煜何楚田恬恬王胜春张锦
李浩 舒炫煜 何楚 田恬恬 王胜春 张锦
摘要:K近邻算法是一种高效且易实现的监督型机器学习算法。对于多分类问题通常将多分类任务拆解为多个二分类任务进行求解,一般采取OVO(一对一)及OVA(一对多)两种机制进行解决。该文主要在鸢尾花数据集上,对两种方式进行比较,仿真结果表明,采用这两种不同的方式处理多分类问题,结果是一致的,但各有优劣。
关键词:一对一策略;一对多策略;K近邻算法
中图分类号:TP18 文献标识码:A 文章编号:1009-3044(2018)36-0230-02
Abstract:KNN algorithm is an efficient and easy to implement supervised machine learning algorithm. For multi-classification problems, multi-classification tasks are usually decomposed into multiple binary tasks to solve. OVO (one versus one) and OVA (one versus all) mechanisms are generally adopted to solve the problem. In this paper, we compare the two methods on Iris data set. The simulation results show that the two methods have the same results, but each has its own advantages.
Key words:One versus one strategy; One versus all strategy; K nearest neighbor algorithm
在现实生活中会经常遇到多分类问题,即待分类样本类别大于2。目前,一般基于支持向量机的多分类问题研究居多。基于SVM的多分类方法主要有2类途径,其中一类是拆解策略,即将一个多分类问题分解成多个二分类问题,通过构造多个SVM二值分类器并将它们组合起来实现多类分类,如“一对一”,“一对多”,“DAG SVM ”等方法[1]。另一类是整体方法,即直接在一个优化公式中同时考虑所有类别的参数优化[2].整体方法慢,分类精度不占优,所以,目前实际应用中还是以“一对一”和“一对多”方法为主。在文献[3],提出决策有向无环图和有向二叉树来处理多分类问题。在文献[4]提出了两个新的K类(K>3)多分类算法:一对一对一即一对一对多算法,实验结果明显提高了识别的精度,因此拆分策略有有效的。
本文利用处理多分类问题的两种拆分策略在鸢尾花数据集上进行对比研究,比较两种拆分策略的优劣性,为后续多分类问题的研究起到一定的指引作用。
1 一对一及一对多策略概述
通常对于多分类任务解决的基本思路是将多分类问题拆解为多个二分类任務进行求解。具体来说,是先对多分类问题进行拆分,然后为拆出的每个二分类任务训练一个分类器;在测试时,对这些分类器的预测结果进行集成以获得最终的多分类结果。通常采用两种经典且容易实现的拆分策略,即一对一(OVO)和一对多(OVA)。
1.1 一对一概述
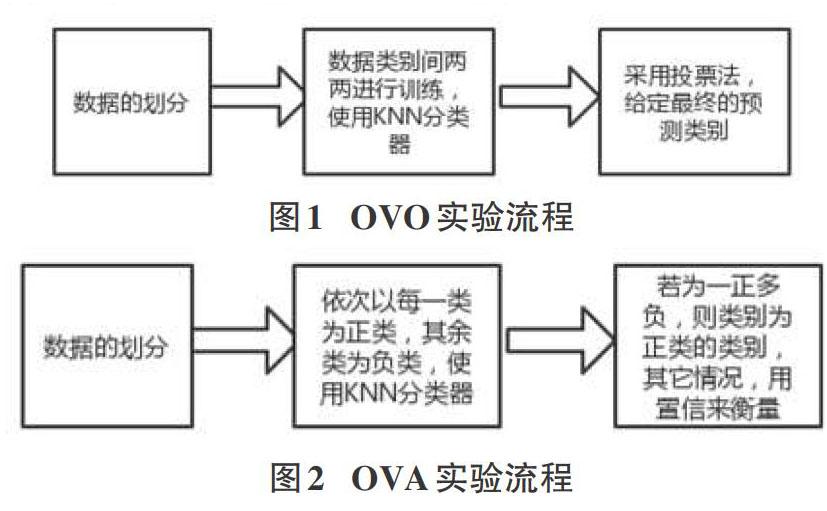
一对一(OVO)拆分策略:将多分类问题进行拆分,若样本具有M个类别,则将数据集划分为M部分,每一部分为一个类别,然后将这M部分两两配对,因此可形成M(M-1)/2个二分类任务,即可训练M(M-1)/2个分类器,可得到M(M-1)/2个预测结果,最后用投票法决定测试样本的最终预测类别:把被预测得最多的类别作为最终的分类结果。
1.2 一对多概述
一对多(OVA)拆分策略:将多分类问题进行拆分,若样本具有M个类别,则将数据集划分为M部分,每一部分为一个类别,与OVO不同的是,使用训练时的分类器数目与参与训练的数据不同。OVA只需要M个训练器,即只形成M个二分类任务,因此参与训练的数据与OVO不同,它是依次分别以每一类别为正类,其余类别的数据集统一带上负类的标签,也就是将其余数据集的标签重新打上。若最终各个分类器的预测结果出现一正多负的情形,则将最终的预测类别附上所在正类的样本标签;若出现结果为多正多负的情形,则最终的预测类别为置信度最高的正类样本的标签。
2 OVO及OVA比较研究
2.1 数据集介绍
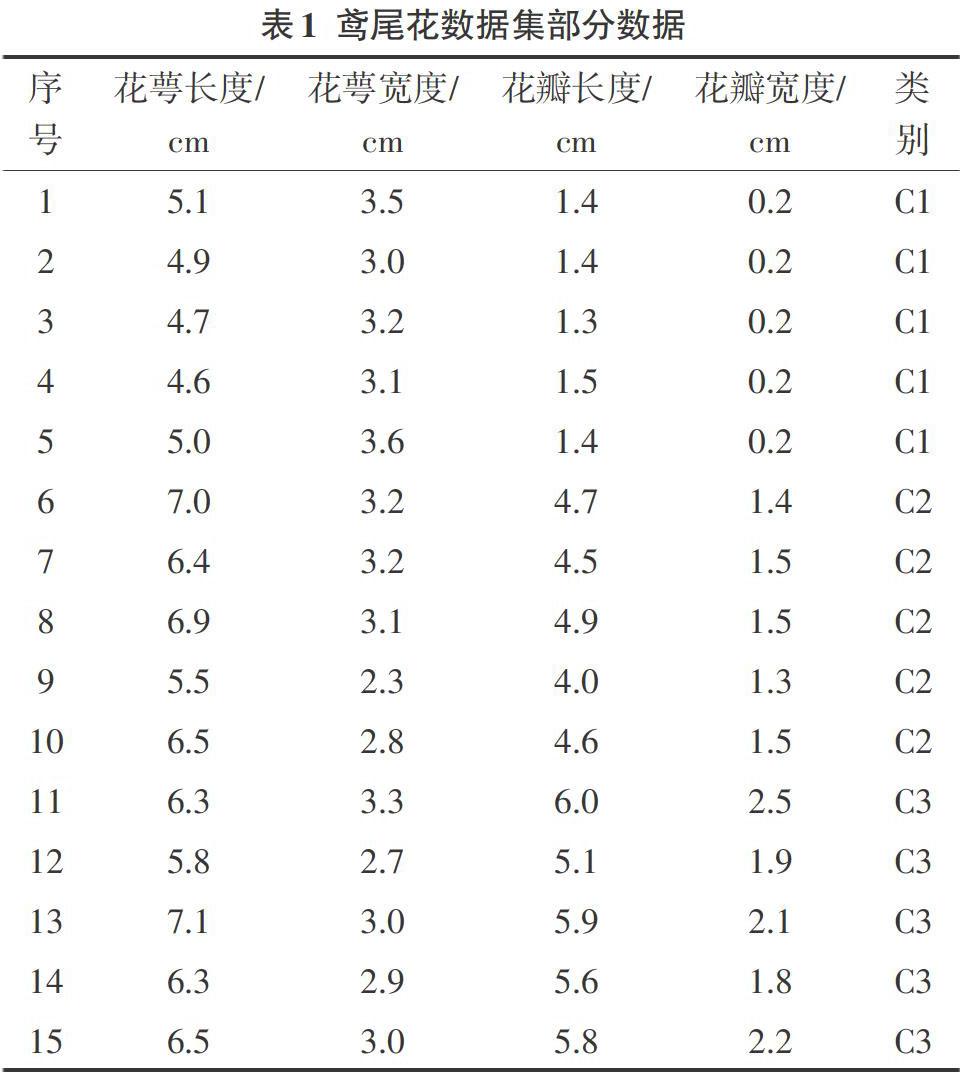
此次研究选取UCI标准数据库中的鸢尾花数据集,该数据集是常用于分类的,是一类多重变量分析的数据集,数据集具有150个样本,其中有三个类别,依次是山鸢尾、杂色鸢尾以及维吉尼亚鸢尾,它有四个属性,分别由花萼长度、花萼宽度、花瓣长度及花瓣宽度构成,类别比值为50:50:50,所用的鸢尾花数据集部分数据如表1所示。
2.2 一对一及一对多实验流程
采用OVO及OVA方式处理多分类问题,首先进行的是数据的划分,数据有M类别,则划分为M部分,每一部分代表一个类别,然后都采用KNN算法作为分类器,因为K近邻算法是一种高效且易实现的监督型机器学习算法。
2.3 结果分析
本文所有实验全部在 Windows 7操作系统下完成,选用 UCI数据集上的鸢尾花数据集,基于MATLAB对OVO及OVA两种解决多分类问题的方法进行仿真实验。实验分两组进行,从不同角度比较OVO及OVA方法的优劣性。
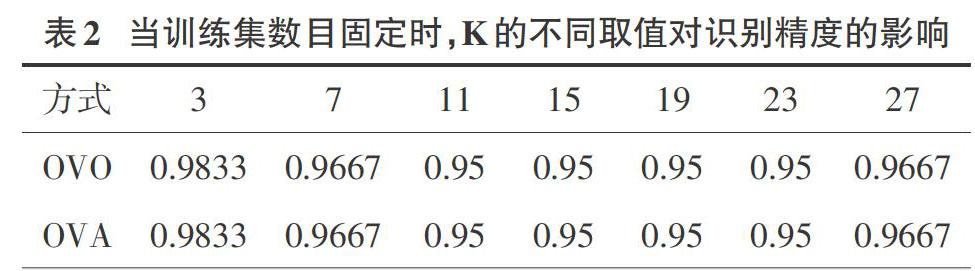
实验1:实验选取90个鸢尾花训练样本集,60个鸢尾花测试样本集,固定训练集与样本集的数目,取不同K近邻数目,比较两种方式在不同K值下的识别精度。
分析:当训练集数目固定时,在训练集样本为90个,测试集样本为60个时,两种方式所得到的实验结果是一样的,但是在采用OVO方式处理问题时,可能会出现投票数相同的情况,则对最终的预测结果产生影响,而OVA的方式则不会出现此种情况,当出现时则将置信度大的类别判为最终预测类别。
实验2:固定K的取值,当K=5时,训练集样本不断增加,比较两种方式的识别精度。
分析:当K值固定时,随着训练集样本数目的增加时,两种方式所得到的实验结果是一致的。
3 结论
在鸢尾花数据集上用两种处理多分类问题的方式,进行比较研究,发现两种方式的结果是一样的,但当数据集增大,类别增多时,用OVO方式处理多分类问题较为复杂,因为要训练M(M-1)/2个分类器,也易在投票环节出现最多类票数相同情况,而用OVA方式去处理多分类问题,其分类器的个数在减少,但在训练模型的时候,正类数据与负类数据会出现不平衡情况,当这种不平衡比例增大时,会影响分类的结果。因此,在一般情况下,两种方式处理多分类问题,效果差不多,但两种方法各有优劣。在后一阶段的工作中,看能否寻找一种结合两者优势的方式去解决多分类问题。
参考文献:
[1] HsuChih-wei,LinChih-jen.A comparisonof methodsfor multiclasssupportvectormachines[J].IEEE Transactionson NeuralNetworks,2002,13(2):415-425.
[2] Bredensteiner E J , Bennett K P. Multicategory Classification by Support Vector Machines[J]. Computational Optimization and Applications, 1999, 12(1-3):53-79.
[3] 任進军,陈军. 基于层次结构的多分类算法研究[J]. 贵州大学学报:自然科学版,2017(4):59-63.
[4] 翟佳,胡毅庆,成小伟.基于三分类支持向量机的多分类算法研究[J].中北大学学报:自然科学版,2015(5):520-525.
[通联编辑:唐一东]
