金属结合能、线膨胀系数及德拜温度的解析研究与计算
2018-03-03于长丰
于长丰
(西安工程大学 理学院 物理系,陕西 西安710048)
(10)
方程组(8)中,金属的结合能De和待定系数a为未知数,力常量f2和f3为中间变量,可以通过金属的其他物性参量如线膨胀系数、德拜温度等间接求出. 式(8)中N1,N2,q1和q2为由n值决定的常量,根据式(9)和式(10)进行计算,计算结果见表1.
2 金属结合能与线膨胀系数、德拜温度之间的关联性
在方程组(8)中只要知道了二阶力常量f2和三阶力常量f3便可计算出金属的结合能De和势能函数中的待定系数a. 由金属物理知识可知,二阶力常量f2和金属原子谐振频率ωe之间满足
(11)
其中μ为金属原子的约化质量,对于同一种金属,则有
(12)

(13)
式中γ为关联因子. 但在式(8)中,三阶力常量f3还是未知,可以根据金属线膨胀系数α与力常量的关系定出f3. 根据玻尔兹曼统计法[11,24],可知金属在平衡核间距处的三阶力常量f3与二阶力常量f2及线膨胀系数α的关系为
(14)
将式(11)~(14)代入式(8)整理得:
(15)
(16)
(17)
式(15)即适用于多种不同晶系的关于金属结合能、线膨胀系数及德拜温度之间的关联方程. 式中p1和p2针对n不同而取不同的值,且p1=N1/2,p2=N2/N1,γ为关联因子,其大小为γ≈1~1.1,不同的金属略有不同.p1和p2取值如表1所示.

表1 不同n值下的系数
将玻尔兹曼常量、普朗克常量及质子质量代入式(15)和(16)得:
(18)
(19)
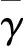

另外需要指出的是,文献中给出的线膨胀系数和德拜温度均是常温下的数值或平均值,而金属的这2个性能指标都是随环境温度或压力的改变而变化的[7,16-17,31],在本文计算中均尚未考虑这种变化的影响.
3 金属线膨胀系数、德拜温度的理论计算
由式(18)可以给出金属线膨胀系数和德拜温度的解析计算式为
(20)
(21)
将式(17)及k值代入式(20)及(21)得
(22)
(23)
在表3线膨胀系数和德拜温度计算中尚未考虑温度或压力的影响,如果考虑这种影响,对于给定的金属元素,设Re,α及θ是温度T或压力p的函数,则由式(20),p为常量时有
(24)
T为常量时
(25)
若平衡核间距、线膨胀系数及德拜温度同时是温度T和压力p的函数,由式(20)得

(26)
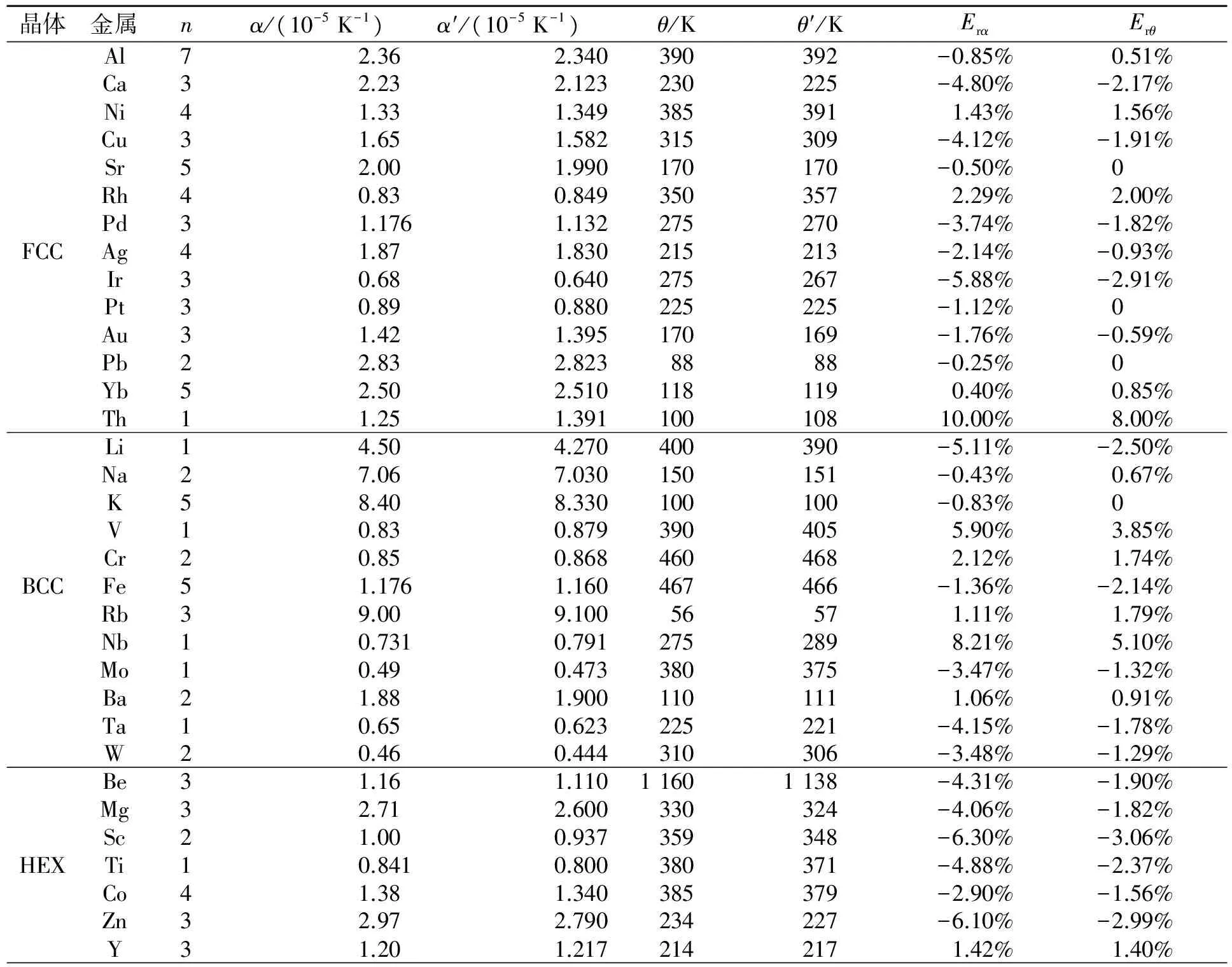
表3 线膨胀系数与德拜温度理论计算值

续表3
4 结 论
采用两体势模型研究了不同晶体结构的共53种金属的结合能、线膨胀系数、德拜温度之间的关联特性并给出了适用于多种不同晶系的三者之间的关联方程[式(15)],在该方程中存在共同的关联因子,其均值为1.046,相对均方根误差为2.17%. 由关联方程进一步导出了金属线膨胀系数和德拜温度解析计算式,理论计算出的53种金属的线膨胀系数、德拜温度与实验值均吻合,其平均相对误差分别2.9%和1.66%,相对均方根误差分别为3.75%和2.19%.
[1] Lekka C E, Bernstein N, Papaconstantopoulos D A, et al. Properties of bcc metals by tight-binding total energy simulations [J]. Mater. Sci. Eng. B, 2009,163(1):8-16.
[2] Zhang Bo, Li Xiaobo, Li Dan. Assessment of thermal expansion coefficient for pure metals [J]. Calphad, 2013,43:7-17.
[3] Feller H G. Influence of binding energy on tribological behavior of pure metals [J]. Metall, 1985,39(5):431-435.
[4] Buch A. Mechanical and physical properties of metals-relation to inter-atomic bond forces [J]. Materialfung/Materials Testing (Materialpruefung), 2003,45(9):387-393.
[5] Buch A. Correlation between magnitude sequence of Young’s moduli and physical properties of pure metals [J]. Materialfung/Materials Testing(Materialpruefung), 2006,48(6):289-292.
[6] Kouam J, Rochegude P. On the prediction of thermal expansion of metals [J]. J. Mater. Sci. Lett., 1996,15(7):600-602.
[7] ZHANG Mei-guang, YAN Hai-yan, WEI Qun, et al. Elastic and thermodynamic properties of Re2N at high pressure and high temperature [J]. Transactions of Nonferrous Metals Society of China, 2013,23(12):3714-3721.
[8] Zhu Y F, Lian J S, Jiang Q. Modeling of the melting point, Debye temperature, thermal expansion coefficient, and the specific heat of nanostructured materials [J]. J. Phys. Chem. C, 2009,113(39):16896-16900.
[9] 钱存富,陈秀芳,余瑞璜. 锕系金属结合能的计算[J]. 中国科学(A辑),1997,27(1):72-76.
[10] 郑伟涛,余瑞璜. 贵金属的结合能、体膨胀系数的研究[J]. 金属科学与工艺,1991,10(4):24-28.
[11] 郑国桢,林苗华,林德明. 金属材料热膨胀系数经验公式的探讨[J]. 广东工业大学学报,1999,16(3):1-8.
[12] 孟振华,李俊斌,郭永权,等. 稀土元素的价电子结构和熔点、结合能的关联性[J]. 物理学报,2012,61(10):107101.
[13] 于长丰,蒋学芳,成鹏飞,等. 金属线膨胀系数、德拜温度和杨氏模量之间关联特性[J]. 物理实验,2012,32(8):37-40.
[14] Pirog I V, Nedoseikina T I. Study of effective pair potentials in cubic metals [J]. Phys. B: Condensed Matter, 2003,334(1/2):123-129.
[15] Grad G B, Bonzi E V. First principles study of the binding energies of pure metals using FP-LAPW method [J]. Journal of Electron Spectroscopy and Related Phenomena, 2013,189(15):45-50.
[16] Xu G L, Chen J D, Xia Y Z, et al. Pseudo-potential investigations of structural, elastic and thermal properties of tungsten disilicide [J]. Chine. Phys. B, 2009,18(8):3495-3499.
[17] Liu X K, Liu C, Zheng Z, et al. First-principles investigation on the structural and elastic properties of cubic-Fe2TiAl under high pressures [J]. Chin. Phys. B, 2013,22(8):087102.
[18] 闵婷,高义民,李烨飞,等. 第一性原理研究碳化铬的电子结构、硬度和德拜温度[J]. 稀有金属材料与工程,2012,41(2)271-275.
[19] 伊利亚 G. 卡普兰.分子间相互作用:物理图象、计算方法与模型势能[M]. 北京:化学工业出版社,2013:148-197.
[20] 张邦维,胡望宇,舒小林. 嵌入原子方法理论及其在材料科学中的应用:原子尺度材料设计理论[M]. 长沙:湖南大学出版社,2003:88,212,222,291,230,249-250,291-292.
[21] 于长丰. 普适性双原子分子解析势能函数的研究[J]. 光谱学与光谱分析,2012,32(8):2056-2060.
[22] 于长丰,王志伟. 六参数高精度双原子分子解析势能函数[J]. 计算物理,2012,29(4):566-574.
[23] Yu C F, Yan X A. A high precision analytic potential function applied to diatomic molecules and ions [J]. Journal of Shenzhen University Science and Engineering, 2014,31(6):561-569.
[24] 于长丰. 相位力学原理[M]. 北京:国防工业出版社,2007:26-233.
[25] 于长丰. 金属单晶体杨氏模量的微观定量研究[J]. 吉林大学学报(理学版),2005,43(1):73-78.
[26] 于长丰,宋立勋,刘代志. 核素比结合能的两个新解析计算式[C]//中国数学力学物理学高新技术交叉研究学会第十二届学术年会论文集. 北京,2008:70-75.
[27] 于长丰,王晓娟,朱长军,等. 核素β稳定线的解析研究[J]. 浙江大学学报(理学版),2010,37(4):416-420.
[28] 韦丹. 固体物理[M]. 北京:清华大学出版社,2003:8,91-98,242-243.
[29] 连法增. 材料物理性能[M]. 沈阳:东北大学出版社,2005:159-164,174,252-259.
[30] 李立碑,孙玉福. 金属材料物理性能手册[M]. 北京:机械工业出版社,2011:62,63,505-510.
[31] 聂耀庄,谢佑卿,彭红建,等. 金属Ti热学性质第一原理研究[J]. 中南大学学报(自然科学版),2007,38(6):1072-1077.
