动静弹碰模型及应用
2018-03-03徐华东
徐华东
(湖北省襄阳致远中学)
现对“动静弹碰”模型加以阐述:在光滑水平面上质量为m1的小球以速度v1与质量为m2的静止小球发生弹性正碰。根据动量守恒和机械能守恒:
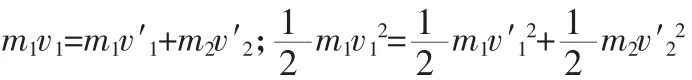
(1)若m1>m2,v′1和v′2都是正值,表示v′1和v′2都与v1方向同向。(若m1>m2,v′1=v1,v′2=2v1,表示m1的速度不变,m2以 2v1的速度被撞出去)
(2)若m1<m2,v′1为负值,表示v′1与v1方向反向,m1被弹回。(若m1<m2,v′1=-v1,v′2=0,表示m1被反向以原速率弹回,而m2仍静止)
(3)若m1=m2,则有v′1=0,v′2=v1,即碰撞后两球速度互换。
这类模型可以用一首诗总结其发生的条件、运用的定理、计算的结果:“动静弹碰两守恒,碰后速度要分清。正比初速反总质,静乘双动动乘差。”“动静弹碰”指出了发生的条件:一小球以某一速度与另一静止的小球发生弹性正碰;“两守恒”指出了应用的规律:动量守恒和机械能守恒,可以列出两个方程;“正比初速反总质”指计算的结果:碰后的两个小球的速度均与初速度成正比,与总质量成反比;“静乘双动”指原来静止的被碰小球的速度在上述基础上还要乘上两倍的入射小球的质量;“动乘差”指原来运动的入射小球的速度在上述基础上还要乘上两小球的质量之差。碰到这类问题首先要分析碰撞的条件,是否属于“动静弹碰”,如果题目中出现一静一动的物体,而且指出如“两弹性小球发生正碰”“两物体正碰,没有机械能损失”,还有像“氦核与静止的质子发生正碰”等,都符合这一模型。接着就可以列出动量守恒和机械能守恒的方程,结果也不用再计算,直接按上述说的写就可以了。这样,既节省了时间,又提高了解题的准确度。
以下以具体例子加以说明。
例1.如图,在足够长的光滑水平面上,物体A、B、C位于同一直线上,A位于B、C之间。A的质量为m,B、C的质量都为M,三者都处于静止状态,现使A以某一速度向右运动,求m和M之间满足什么条件才能使A只与B、C各发生一次碰撞。设物体间的碰撞都是弹性的。

【解析】设A运动的初速度为v0,
A向右运动与C发生碰撞,根据弹性碰撞可得
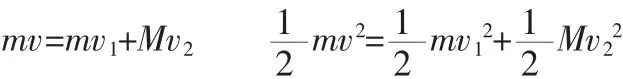
要使得A与B发生碰撞,需要满足v1<0,即m<M
A反向向左运动与B发生碰撞过程,弹性碰撞
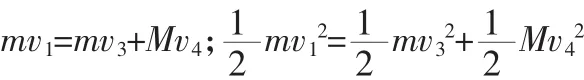
由于m<M,所以A还会向右运动,根据要求不发生第二次碰撞,需要满足v3<v2
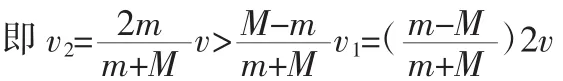
整理可得m2-4Mm>M2解方程可得
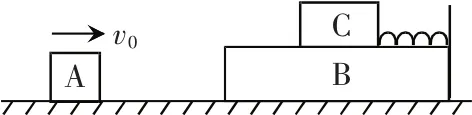
例2.如图所示,在光滑水平面上,木块A的质量mA=1kg,木块B的质量mB=4kg,质量mC=2kg的木块C置于足够长的木块B上,B、C之间用一轻弹簧相拴接并且接触面光滑。开始时B、C静止,A以v0=10m/s的初速度向右运动,与B碰撞后B的速度为3.5m/s,碰撞时间极短。求
(1)A、B碰撞后A的速度。
(2)弹簧第一次恢复原长时C的速度。
【解析】
①因碰撞时间极短,A、B碰撞时,C的速度为零,A的初速度方向为正方向,由动量守恒定律得

代入数据解得vA=-4m/s,方向与A的初速度方向相反。
②第一次恢复原长,弹性势能为零,设此时B的速度为vB′,C的速度为vC
说明:B、C相互作用的过程中,当弹簧恢复原长时,相当于动静弹碰模型。
[1]辜永腾,李敏,穆科佑,等.物理教学中动量守恒定律的重要意义[J].当代教育实践与教学研究,2017.
[2]邱晓燕,唐志海.一道力学碰撞问题中动量守恒与角动量守恒辨析[J].物理教学探讨,2011,29(11):40-41.
