基于灰色预测的船舶航向简捷鲁棒控制
2018-03-02姜日凡,张显库
姜 日 凡, 张 显 库
( 1.大连海事大学 航海学院, 辽宁 大连 116026;2.大连工业大学 网络信息中心, 辽宁 大连 116034 )
0 引 言
船舶航向保持一直是船舶运动控制领域中十分重要的研究方向,因此国内外许多研究人员为改善船舶的操纵性能而一直努力。随着自动控制理论的不停发展,形成很多新的控制算法,如神经网络、模糊控制、鲁棒控制、智能控制等[1-4],但这些都是依据系统已经发生的状态进行控制,属于常规的船舶航向保持控制。
船舶在海上的运动显现出大时滞和非线性等特性,由于大时滞的存在,当给船舶施加一个控制量后,要通过较长的滞后时间才可以看到控制的效果。应用常规的控制很难达到理想的控制效果,而预测控制[5-6]对时滞系统有较好的控制效果,因此预测算法被应用到船舶航向保持控制器的设计中。吕进等[7]设计了船舶航向的神经网络二阶导数多步预测模型及其辨识和预测算法。齐亮等[8]提出基于支持向量机设计船舶非线性系统的广义预测控制算法。徐云厚等[9]提出基于变结构径向基函数神经网络的预测PID船舶航向控制器。这些预测算法能有效解决船舶的大时滞和非线性等问题,但算法较复杂,计算量大。本研究采用灰色预测和鲁棒控制相结合的方法,采用改进的灰色模型对船舶航向偏差进行实时预测,并将预测值应用于船舶航向简捷鲁棒控制器。不仅能针对船舶在海上运动的大时滞和非线性特点进行有效预算,而且具有算法较简单、需要的信息少、计算量小等特点。
1 灰色预测模型
灰色系统是指那些一部分信息明确,一部分信息不明确的系统[10]。而灰色预测可以经过整理原始数据和创建灰色模型来发现和了解系统的发展规律,并对系统的变化趋势进行提前预测,因此灰色预测越来越多应用于控制领域[11-13]。
1.1 GM(1,1)基本预测模型
GM(1,1)基本预测模型的算法只需辨识出两个基本模型参数(发展系数a和灰色作用量b),并且预测也只需要很少的原始数据[10]。
设原始数据列为
X(0)={X(0)(i),i=1,2,…,n}
(1)
对式(1)进行一次累加生成(1-AGO),得到
X(1)={X(1)(k),k=1,2,…,n}
(2)
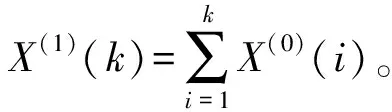
对X(1)可建立白化形式的微分方程

(3)
式中,X(1)={X(1)(k),k=1,2,…,n}。
根据背景值
Z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)
构造紧邻均值生成序列。

a^
=[a,b]T可用最小二乘法辨识得到

=(BTB)-1BTYn
(4)

Yn=(X(0)(2),X(0)(3),…,X(0)(n))T。
通过累减生成还原,可得还原值
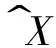
X^
(0)(k+1)=
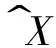
X^
(1)(k+1)-
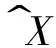
X^
(1)(k)=
(5)
1.2 改进的GM(1,1)预测模型
传统的GM(1,1)预测模型精确度较低,为了进一步提高模型精确度,采用等维新息和修改背景值法对传统GM(1,1)模型进行改进。等维新息模型指在原始数据列中增加一个新数据信息,同时要去掉一个最旧数据信息,但用于建模的原始数据列维数要一直不变,数据和模型要一直保持最新,能实现“滚动”式预测,可以提高预测的精确度。比如:
X(0)={X(0)(1),X(0)(2),…,X(0)(n)}
作等维处理可得
X(0)={X(0)(2),X(0)(3),…,X(0)(n+1)}
对于n的选取,经过反复试验比较选定n=5。同时根据灰色模型的指数特性,采用文献[14]中区间求积分法对背景值进行改进,令
(6)
式中,k=1,2,3,…,n。
得出新的背景值公式,应用新背景值能减少模型预测值与原始值的误差,可以提高预测的精确度。
2 简捷鲁棒控制器的设计
闭环增益成形算法是H∞鲁棒控制理论的工程应用简化。当确定了闭环系统补灵敏度函数T的最后希望形状后,利用T的最大奇异值、带宽频率、关门斜率和闭环频谱峰值4个参数能直接构造出鲁棒控制器,是一种简捷鲁棒控制。使用该控制算法设计的控制器阶次低,而且具有良好的控制性能和鲁棒稳定性[15-16]。
船舶航向保持是单输入单输出控制。当取舵角δ为船舶输入,航向ψ为船舶输出时,能得到船舶的Nomoto传递函数数学模型[17-18]
(7)
鲁棒控制器K使用三阶闭环增益成形算法设计,当闭环系统的高频渐近线斜率取-60 dB/dec时,求取标准反馈系统的闭环增益成形控制器,采用文献[15]中的三阶闭环增益成形控制器
(8)
将灰色预测的预测离散值应用于简捷鲁棒控制器,因此控制器要采用离散型三阶闭环增益成形算法设计[19]。首先对传递函数数学模型离散化,采用双线性变换法对式(7)进行离散,得到
(9)
再对式(8)使用双线性变换法进行离散,得到
(10)
式中:

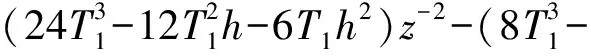
将式(9)代入式(10)就可得到最终的离散型三阶闭环增益成形控制器。
3 仿真与结果分析
仿真以大连海事大学实习船“育鲲”轮为被控对象,通过船舶参数能计算出满载时的船舶Nomoto 模型中参数K0=0.31 s-1,T0=62 s,取T1=3可使闭环控制系统将海浪的频谱滤除掉,h=1 s。仿真时使用非线性响应型数学模型,非线性参数α=7.93,β=4 100.46。
针对海风干扰,使用简单的白噪声来实现。针对海浪干扰,使用简单的模拟方法,通过白噪声驱动一个典型的二阶振荡环节,白噪声的采样时间为0.2 s,其Noise Power参数设置为0.000 1,则在6级风作用下得到的海浪传递函数
(11)
图1给出了使用Matlab的Simulink实现的仿真框。假定船舶的时滞为固定时间,船舶设定航向为30°,仿真时间为600 s,船舶分别使用常规PID控制算法、基于GM(1,1)的简捷鲁棒控制算法、基于改进的GM(1,1)的简捷鲁棒控制算法进行以下3种情况的输出航向对比仿真研究。
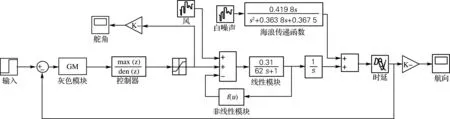
图1 Simulink仿真框
(1)当无风浪流干扰、无时滞,无干扰船舶输出航向的对比仿真曲线如图2所示。
(2)当风力为6级、风向为50°,而时滞小于采样周期,采样周期为1 s,时滞为0.7 s时,小时滞船舶输出航向的对比仿真曲线如图3所示。
(3)当风力为6级、风向为50°,而时滞大于采样周期,采样周期为1 s,时滞为9 s时,大时滞船舶输出航向的对比仿真曲线如图4所示。
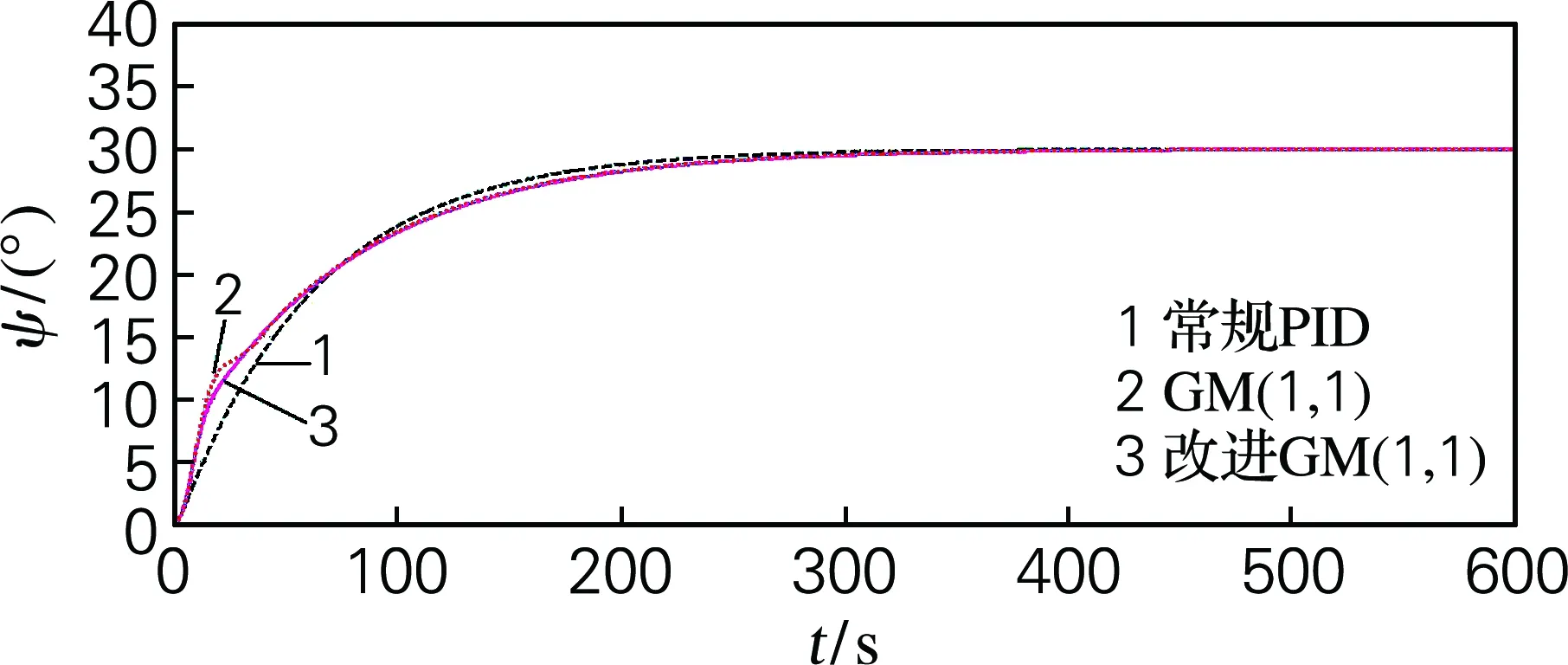
图2 无干扰船舶输出航向的仿真对比结果
从图2中可以看出,在无风浪流干扰、无时滞情况下3种船舶控制器的输出航向都无超调,都能在300 s以后稳定到30°,3种控制效果理想。
从图3中可以看出,在风力为6级、时滞小于采样周期的情况下,常规PID控制器的输出航向有较小的超调,航向误差±1°;GM(1,1)和改进的GM(1,1)控制器的输出航向都无超调,航向误差±0.5°;3种船舶控制器都能在300 s以后稳定到30°,控制效果较为理想。
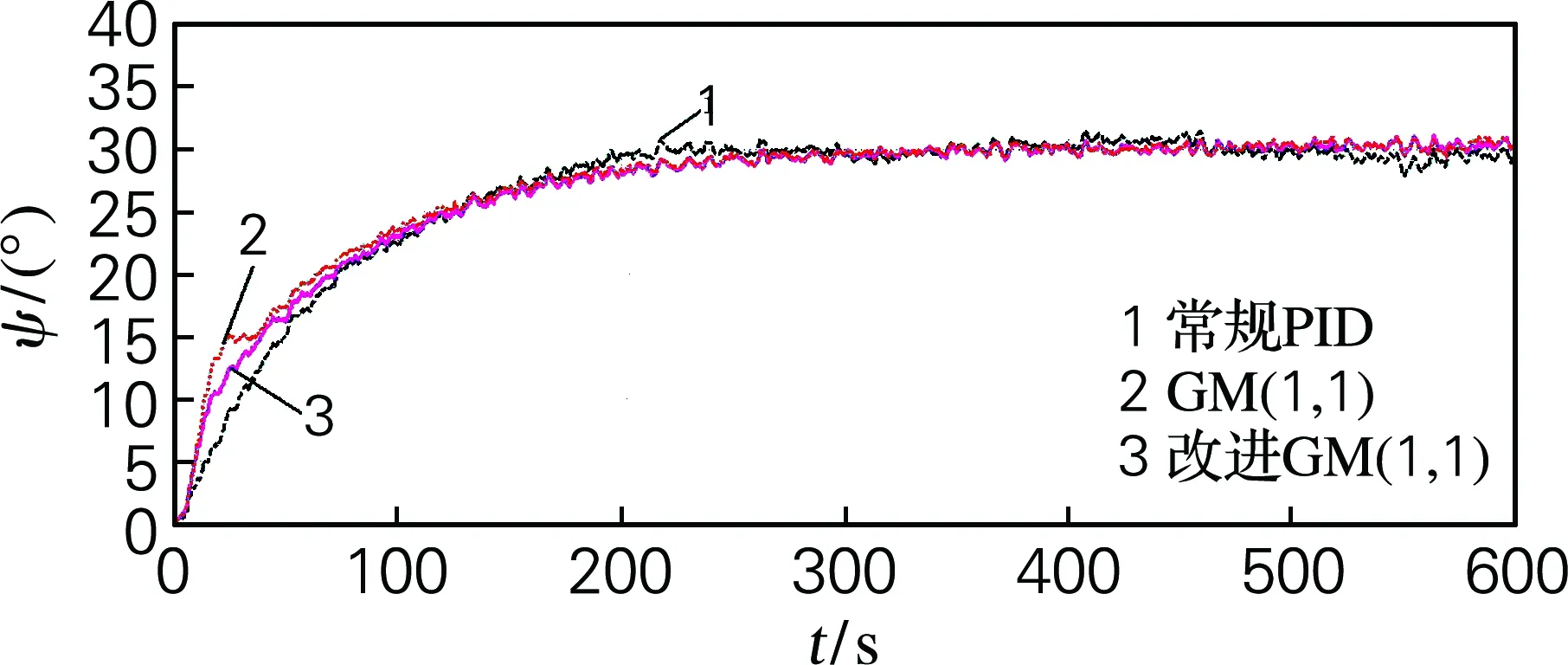
图3 小时滞船舶输出航向的仿真结果
从图4中可以看出,在风力为6级、时滞大于采样周期的情况下,常规PID控制器的输出航向有较大的超调和振荡,航向误差±5°,控制效果差;GM(1,1)控制器的输出航向有较小的超调,400 s以后基本稳定到30°左右,航向误差为±1°;改进的GM(1,1)控制器的输出航向无超调,300 s 以后基本稳定到30°左右,航向误差为±0.5°,船舶控制效果较为理想,能够达到对船舶航向保持控制的目的。

图4 大时滞船舶输出航向的仿真结果
4 结 论
通过仿真曲线可以看出,在恶劣海况和有时滞情况下,灰色预测简捷鲁棒控制与常规PID控制相比,运用了灰色预测的超前控制特性,提高了船舶航向稳定性,具有更好的控制效果;同时在时滞大于采样周期的情况下,采用改进的GM(1,1)模型比传统GM(1,1)模型预测精度更高和控制效果更好。仿真结果表明,在假设条件下针对船舶的大时滞和非线性情况,所设计的方法是可行和有效的,具有较强的鲁棒性。仿真实验的船舶时滞为固定时间,但实际中很多时滞是随机的和不确定的,因此今后工作应该在船舶时滞为随机和不确定的情况下对算法进一步改进,优化预测效果,得到更理想的控制效果。
[1] VELAGIC J, VUKIC Z, OMERDIC E. Adaptive fuzzy ship autopilot for track-keeping[J]. Control Engineering Practice, 2003, 4(11): 433-443.
[2] TAHOUN A H, ABOUELSOUD A A, MAHMOUD M S, et al. An approach for robust SISO adaptive control[J]. Mediterranean Journal of Measurement and Control, 2006, 2(4): 186-193.
[3] ZHANG X K, ZHANG G Q. Design of ship course-keeping autopilot using a sine function based nonlinear feedback technique[J]. Journal of Navigation, 2016, 69(2): 246-256.
[4] 张显库,张国庆,陈秀嘉.一种非线性反馈反步递推算法的线性弱化[J].控制与决策,2015,30(9):1641-1645.
[5] 席裕庚.预测控制[M].北京:国防工业出版社,1993.
[6] MAN G N. Auto-tuned PID controller using a model predictive control method for the steam generator water level[J]. IEEE Transactions on Nuclear Science, 2001, 48(5): 1664-1671.
[7] 吕进,郭晨.船舶航向的神经网络二阶导数多步预测模糊自适应控制[J].大连海事大学学报,2006,32(3):1-4.
[8] 齐亮,俞孟蕻.基于支持向量机的船舶航向广义预测控制研究[J].中国航海,2007,72(3):54-56.
[9] 徐云厚,涂亮,李智,等.基于变结构径向基函数网络的船舶运动预测PID控制[J].控制理论与应用,2010,27(11):1564-1568.
[10] 褚晓琳.基于灰色系统理论的北京市对外贸易预测[J].中国流通经济,2011,25(5):54-58.
[11] 施小成,刘振业,付明玉,等.灰色预测GA-PID全垫升气垫船航向控制[J].计算机仿真,2011,28(8):173-176.
[12] 祝华远,崔亚君,高峰娟.灰色预测模型在军机飞控系统故障预测中的应用[J].四川兵工学报,2014,35(6):44-46.
[13] KAYACAN E, ULUTAS B, KAYNAK O. Grey system theory-based models in time series prediction[J]. Expert Systems with Applications, 2010, 37(2): 1784-1789.
[14] 王钟羡,吴春笃.GM(1,1)改进模型及其应用[J].数学的实践与认识,2003,33(9):20-25.
[15] 徐国平,张显库.基于网络控制的船舶航向简捷鲁棒控制[J].大连海事大学学报,2014,40(1):5-8.
[16] 王立军,张显库.基于鲁棒模糊控制的船舶转向及航向保持[J].中国航海,2011,34(2):1-4.
[17] 张显库,王立军.基于闭环增益成形的船舶舵机间隙非线性抑制算法[J].中国造船,2013,54(4):94-99.
[18] 陈正生,吕志平,张清华,等.基于时间序列分解的GPS卫星钟差预报[J].测绘科学,2011,36(3):116-118.
[19] 张显库.离散型闭环增益成形算法及其应用[J].中国航海,2006,42(3):4-6.
