黑臭水体中不同浓度Fe2+、S2-与DO和水动力关系

王玉琳,汪 靓,华祖林* (1.河海大学浅水湖泊综合治理与资源开发教育部重点实验室,江苏 南京210098；2.河海大学水资源高效利用与工程安全国家工程研究中心,江苏 南京 210098；3.河海大学环境学院,江苏南京 210098)

近年来,我国东部太湖、巢湖等浅水湖泊的水体黑臭现象频繁发生,严重影响沿湖居民的生产和生活水平,对湖泊本身的生态安全构成威胁[1-3].治理黑臭水体是国家“水十条”重要任务,同时也是一项十分艰巨的工作.

湖泊水体黑臭是一种湖泊内生物地球化学循环失衡引起的问题[4]:在适当的气象、水温等条件下,浅水湖泊中藻类大量的聚集和死亡使湖泊中有机物分解导致水体溶解氧(DO)的迅速减少,水体进入缺氧状态[5-7].在此基础上,藻华聚集和有机物分解所形成的厌氧环境使沉积物中高价态的Fe、Mn和S被还原形成Fe2+和S2-等并不断向上覆水体中扩散.大量有机物及耗氧物质进入水体使DO持续降低,破坏了水体中铁、硫循环,造成Fe2+与H2S 大量累积[8-11]. H2S进一步电离成HS-、S2-,与水中的Fe、Mn 等离子结合形成FeS、MnS 等悬浮颗粒,从而导致水体颜色发黑[12],其中FeS是湖泊水体的主要致黑物质[13].藻类死亡分解形成的挥发性有机硫是致使水体发臭的主要物质[14-17].由此可见,Fe2+和S2-的积累是黑臭水体形成的重要因素.

除实验机理研究外,对黑臭水体中环境要素的定量研究主要集中于以线性回归方法研究营养盐、化学需氧量及生化需氧量的变化[18-20];但黑臭水体中Fe2+、S2-浓度及其与环境因子之间的定量关系研究较为罕见.已有研究[21]运用线性空间滞后模型定量分析了黑臭水体中Fe2+、S2-与DO、流速的定量关系,但其方法实质上仍然是基于线性回归.由于普通线性回归关注的是因变量的条件均值,即通过最小二乘法求解自变量为一确定值时,因变量的均值,因此线性回归方法只能给出湖泊中DO、流速等与Fe2+和S2-浓度平均值的关系[22-23].湖泊水体黑臭发生时,水体Fe2+和S2-浓度较高,因此更需要关注不同浓度,特别是高浓度Fe2+、S2-情况下二者与DO和水动力的定量关系.由于分位数回归是求解自变量与因变量不同分位数之间的关系,因此能较好的估计湖泊水体黑臭发生时不同Fe2+、S2-浓度与DO、流速的定量关系.此外,分位数回归不需要假设因变量与自变量分别

满足正态分布[24],这对于通常分布非常复杂的环境和生态数据而言也是一个有吸引力的优势[25].近年来,分位数回归被运用于湖泊营养物输入响应关系[26],空气污染对人体健康的影响[27]及空气的臭氧浓度[28]等的研究;但相比线性回归在环境领域浩如烟海的应用,分位数回归在环境研究中仍然较少被运用.

巢湖作为我国五大淡水湖之一,受人类行为的影响,已成为严重富营养化的浅水湖泊[29-30],其西半湖南淝河口区域水体污染严重,水体黑臭现象频发[31].本文以巢湖南淝河汇流湾区黑臭水体为例,基于分位数回归方法研究了其中DO、流速与高浓度Fe2+、S2-的关系.研究表明DO、流速与黑臭水体区域不同浓度的Fe2+、S2-作用并不一致.同时,分位数回归方法能够有效的描述黑臭水体中DO、流速与不同浓度的Fe2+、S2-关系.这一研究可以为治理浅水湖泊中的黑臭水体提供理论参考.

1 材料与方法

1.1 数学模型

在统计学上,普通的线性回归求解的是因变量Y的数学期望依赖自变量X的变化而改变的方程,即下式.

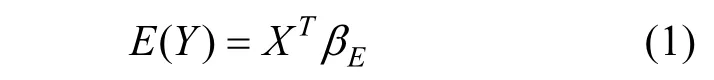
式中:βE是回归系数.

线性回归模型的因变量和自变量都必须满足正态分布才能求得无偏的系数,这限制了线性回归方法的运用范围.而分位数回归则打破了线性回归模型的诸多限制,在某种程度上可以认为是线性回归方法的有力推广.

1.1.1 分位数回归 若观测量Y的分布函数为F(Y),则Y的τ(0＜τ＜1)分位数G(τ)由下式定义.

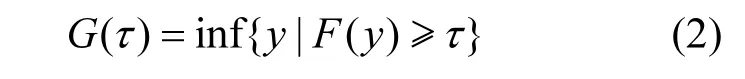
式中: inf表示满足条件的观测值的下确界,在实际中可以简化的用满足条件的最小观测值代替.当求两种不同观测量关系时,假设因变量Y某分位数的值Yτ和自变量X为线性关系,即

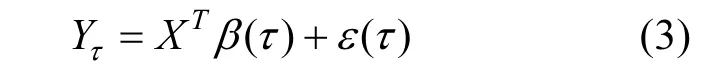
式中:β(τ)是τ分位点的回归系数;ε(τ)为τ分位点的回归误差.当观测量X的值为x时,上式求出的Yτ其实即Y的条件分位数,定义如下.

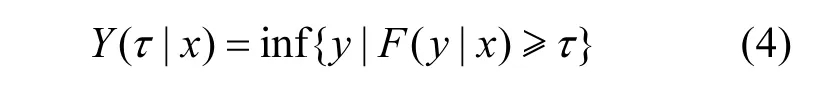
在实际的应用中,式(2)一般写成下式:

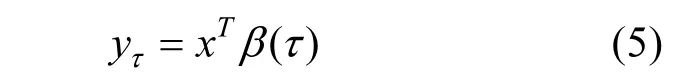
式中: yτ为观测量Y在τ分位数的实际观测结果,x为观测量X的实际观测结果.

1.1.2 模型估计与检验 式(5)中的参数β(τ)可以用推广的最小一乘法来估计,即是求一系列的β(τ),使其满足下式:

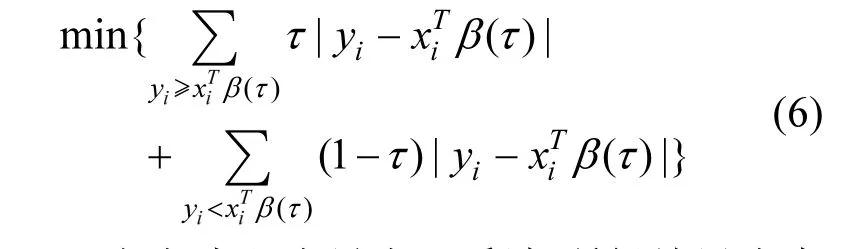
当τ=0.5时,上式即为最小一乘法,所得结果为中位数回归的结果.进一步,若定义损失函数ρ(τ)u如下:

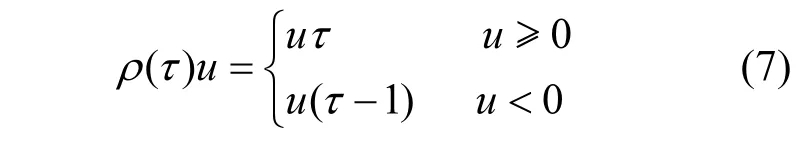
则式(5)可以简单的写成:

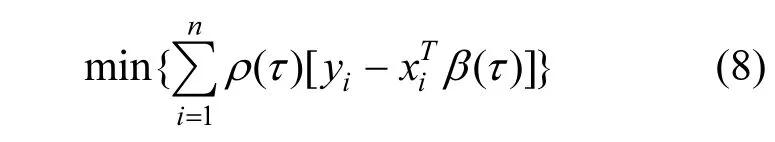
式中: n为观测值的个数.

无论是式(6)还是式(8)的求解都是一个最优化问题,目前比较有效的方法有单纯形法,内点法以及差分等方法[32];本文使用单纯形法求解.

同样,分位数回归模型有统计检验的问题,目前使用较多的是似然比检验[24].本文中分位数回归模型的系数标准差由自助法计算.

1.2 数据来源

统计分析的数据来源于2013年5月与中科院南京湖泊所联合在巢湖南淝河口地区的采样结果.采样点以南淝河口为中心,扇形分布;根据污染物分布特点,在南淝河口对采样点进行了加密;采样点分布如图1所示.

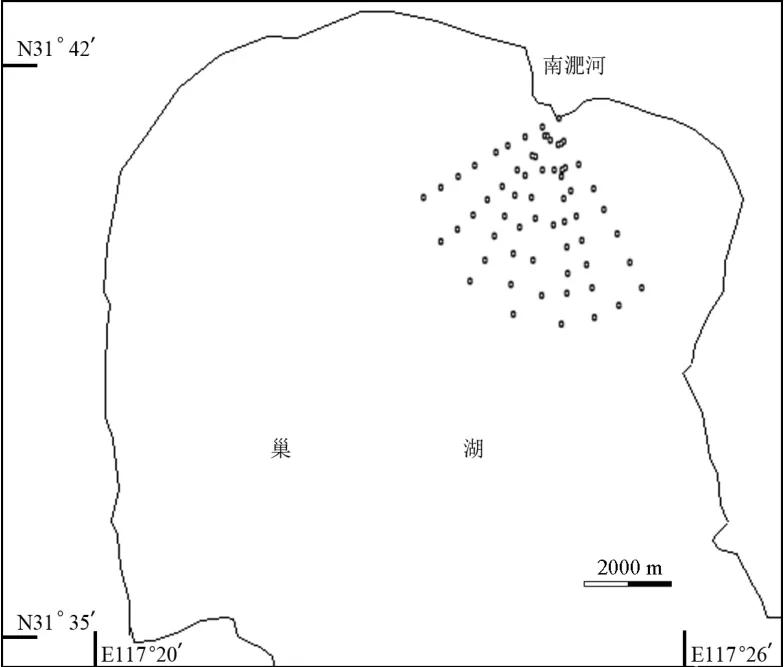
图1 巢湖南淝河口采样点分布Fig.1 The distribution of sampling sites in the Nanfei River estuary of Lake Chaohu

同步采集了水体的流速、溶解氧、Fe2+和S2-等指标;其中,流速采用美国YSI公司的YR-1型声学多普勒流速仪测量;DO用日本HORIBA公司U-53型多参数水质分析仪监测;S2-在实验室采用对氨基二甲基苯胺光度法测定[33];Fe2+按Tamura[34]等改进的邻菲啰啉光度法测定;共得到63组有效数据,其中流速通过连续采样5次,取平均采用; DO, S2-与Fe2+分别做了三个平行,取平均采用.采样时巢湖南淝河口正处于水体黑臭现象较为严重,且肉眼可明显观测到水体发黑的现象;此时,采样数据能较好的代表水体黑臭现象发生时,巢湖南淝河口水体各指标的状况.

2 结果与分析

表1是湖水发生黑臭时,巢湖南淝河口黑臭水体区域Fe2+、S2-与DO、流速的观测值的统计量结果.

表1 观测值主要统计量Table 1 Statistical analysis

从表中的峰度和偏度等特征可以看出,Fe2+、S2-的浓度以及流速都是右偏态分布,偏离正态分布严重;而DO的浓度分布则略有左偏.这样的数据进行普通的回归分析,可能得到错误的回归系数,其误差可以达到50%以上;甚至能影响回归系数的符号,从而在根本上给出错误的关系[24].因此,Fe2+、S2-与DO、流速的关系并不适宜用普通的多元回归方法分析.即使不考虑非高斯分布的影响,普通回归分析也只能得到Fe2+、S2-与DO、流速的平均值的关系,这种关系无法分析黑臭水体中高浓度Fe2+、S2-,低浓度DO的水质特性.

表2是Fe2+、S2-与DO、流速的相关系数及显著性检验结果.相关系数及其显著性检验表明,Fe2+、S2-和流速之间呈显著的负相关关系.这表明通过增强水体交换能力及稀释作用,南淝河入流流量的增大有助于减小该湖湾黑臭水体区域的Fe2+、S2-浓度.从显著性检验结果来看,DO与Fe2+、S2-浓度之间的相关关系并不显著,DO与S2-浓度之间甚至有微弱的正相关性;这结果与DO会氧化Fe2+、S2-成高价态S及Fe的化学机制相矛盾.分析造成矛盾的主要原因为DO与不同浓度的S2-、Fe2+反应速度等化学反应特性有较大差别,而相关系数只能反映它们之间平均的线性关系;由此造成了不合理的结果.这也说明简单的运用线性分析技术研究黑臭水体中DO与Fe2+、S2-浓度的关系会导致非常严重的错误.

表2 相关系数与显著性Table 2 The correlation coefficient and significance test

图2是S2-在0.2～0.8分位数情况下,分别对DO和流速进行分位数回归的结果;表3给出了不同回归模型的流速和DO回归系数及其95%置信区间和显著性检验结果.在实际观测中,S2-浓度的0.2～0.8分位数对应于0.029～0.043mg/L,浓度相差约48%.

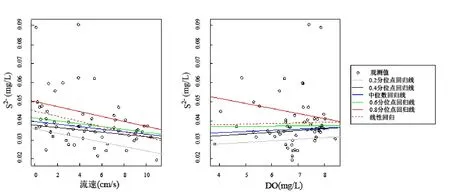
图2 S2-与流速、DO分位数回归Fig.2 Quantile regression among concentrations of S2-, water velocity, and DO

从图2及表3可以看出,不同浓度的S2-与流速之间的关系有很大区别:0.2和0.8分位点下,流速的回归系数分别是-0.00093和-0.00107,且两者均能通过显著性检验;而0.4～0.6分位点下流速的回归系数则不能通过统计检验,即这些分位点情况下流速与S2-浓度之间关系不大.这一结果说明湖体流速的增加可以有效减少黑臭水体中相对低浓度S2-及高浓度S2-区域的污染,但对中等浓度S2-区域的污染影响不大.南淝河是该湖湾区域最主要的Fe2+及S2-来源,黑臭水体污染一般以南淝河口为中心,向湖心区域逐渐减小.分位数回归的结果表明,增加流量对南淝河口本身和黑臭水体外边缘等浓度梯度较大区域的S2-浓度治理效果较好,而对黑臭水体中心区域的S2-浓度无影响.进一步,水体流动对湖体中S2-污染主要有两方面的作用:一是水体流动对污染物等物质的分散作用,使黑臭水体中的S2-分布更为均匀.二是流速会影响水中DO的复氧过程,进而通过氧化作用影响水中Fe2+、S2-等黑臭相关物质的浓度.流速的增加对黑臭水体不同区域的S2-作用不同;这说明流量的增加主要通过第一个途径影响水体中S2-浓度,而水体流动通过增强DO复氧,间接影响S2-浓度的作用较小.

S2-与DO分位回归的结果与流速的结果不同:0.2～0.6分位点下DO的回归系数均为不显著的正值,而只有在0.8分位点即S2-浓度达到0.043mg/L左右时,DO才有显著降低S2-浓度的作用.即充氧对减少南淝河口本身的S2-污染效果较好,而在其它S2-浓度较小的区域则可能效果不佳;这与DO对高浓度S2-的氧化作用效果较好的化学反应机制相符.

通过比较可以发现,在线性回归模型中DO的回归系数为正且无法通过显著性检验,这个线性回归模型几乎是错误的.虽然流速的回归系数与0.8分位点下的回归系数接近,但它不能分析流速对不同浓度、区域S2-的不同作用;而且其系数的95%置信区间也与0.8分位点回归的结果有较大差别;它低估了流动对高浓度S2-的分散作用,约为2.8%;高估了流动对低浓度S2-的分散作用,约为15.5%.线性回归模型不能正确分析得到流速、DO与S2-的定量关系.

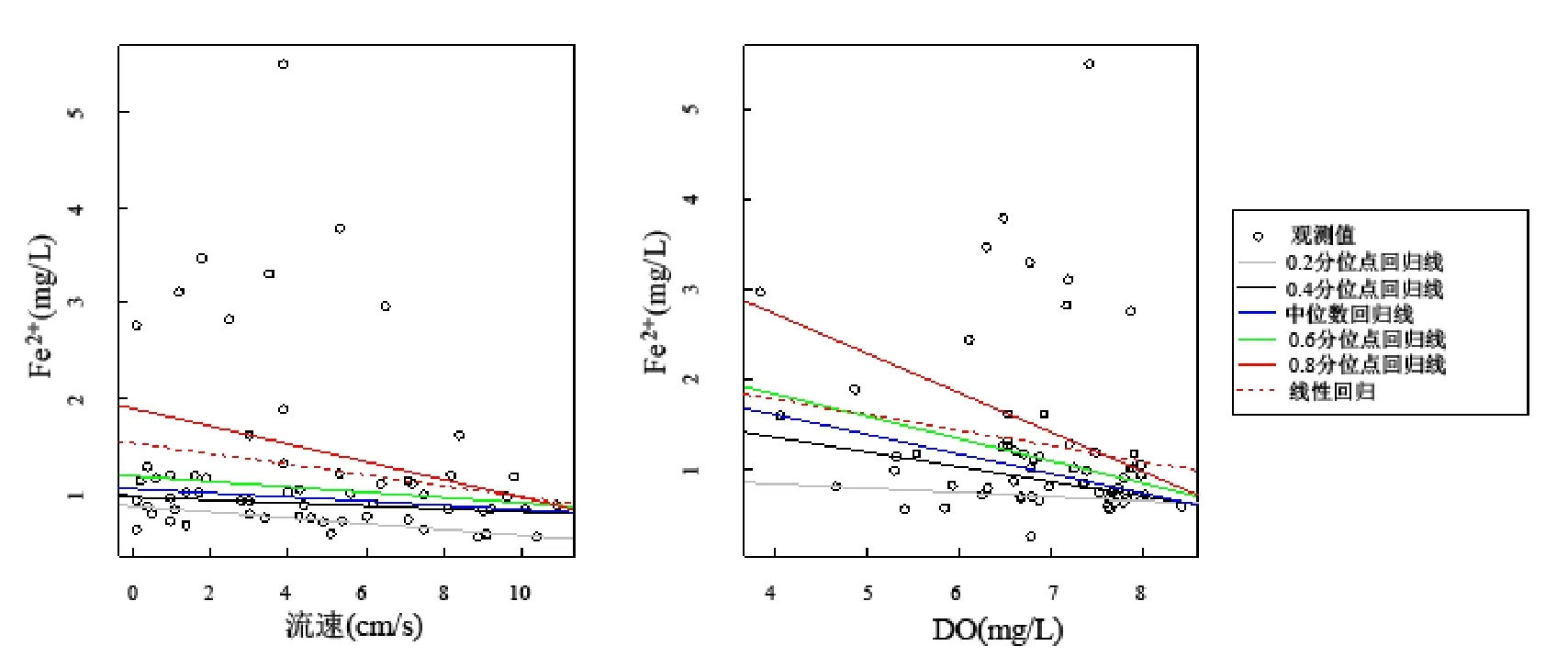
图3 Fe2+与流速、DO分位数回归Fig.3 Quantile regression among concentrations of Fe2+, water velocity and DO

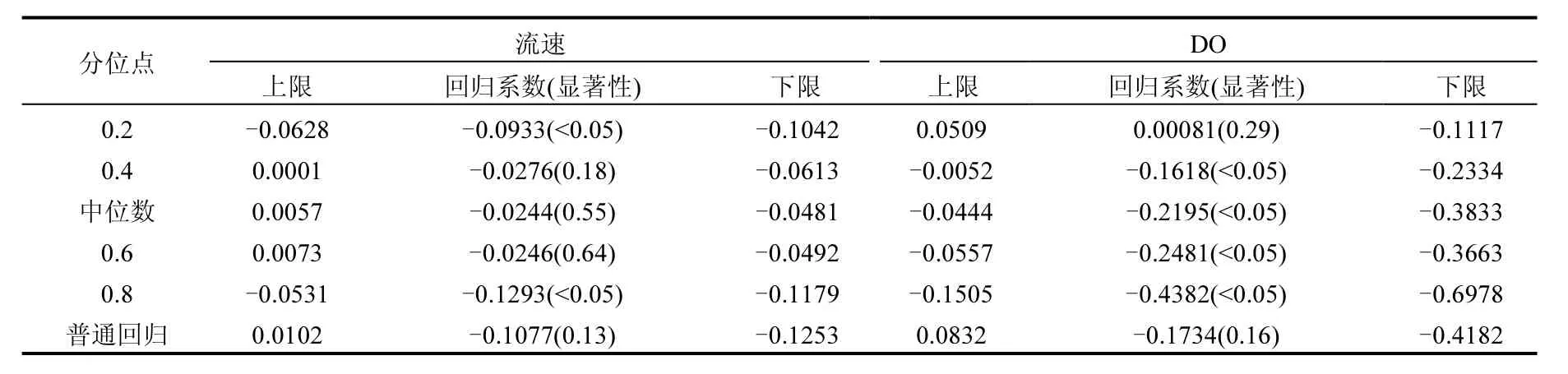
表4 Fe2+模型的回归系数及其95%置信区间Table 4 Regression coefficients and 95% confidence interval of Fe2+ model

图3是Fe2+在0.2～0.8分位数情况下,分别对流速和DO进行分位数回归的结果;表4给出了不同回归模型的流速及DO回归系数及其95%置信区间和显著性检验结果.在实际观测中,Fe2+浓度的0.2～0.8分位数对应于0.69～1.59mg/L,浓度相差约130%.

与对S2-的作用一样,水体流动主要是通过分散作用使黑臭水体中的Fe2+分布更为均匀.增加流速对减少黑臭水体边缘的低浓度Fe2+和南淝河口的高浓度Fe2+的污染有显著作用;在中等浓度Fe2+区域由于其浓度梯度较小,分散作用较弱,因此增加流速对降低该区域Fe2+浓度作用不显著.DO的增加对0.4分位点即0.80mg/L以上的Fe2+有较为显著的氧化作用;且Fe2+浓度越高,氧化作用越强.

普通线性回归错误的估计了流速和DO对Fe2+的作用,在普通线性回归看来,增加流速和DO对降低Fe2+浓度都没有显著作用.总之,线性回归模型不能得到正确的流速、DO和Fe2+、S2-的定量关系;而分位数回归可以分析流速和DO对不同浓度Fe2+、S2-的定量作用,为进一步减少南淝河湖湾区域水体黑臭现象提供理论支持.

3 结论

3.1 根据浓度梯度的不同,增加流速对降低南淝河口的高浓度Fe2+、S2-的污染及黑臭水体边缘低浓度Fe2+、S2-污染有显著的效果;而对黑臭水体中间位置中等浓度Fe2+、S2-污染没有显著影响.

3.2 增加DO浓度只能显著降低黑臭水体中S2-浓度达到0.043mg/L以上,或Fe2+浓度达到0.80mg/L以上区域的污染,且S2-和Fe2+浓度越大,效果越好.增加DO对低浓度Fe2+、S2-污染的处理效果不佳.

3.3 与普通线性回归结果比较:分位数回归方法能够定量分析流速和DO对不同浓度Fe2+、S2-的作用,其结果与线性回归结果有显著差异;而普通线性回归则无法准确的给出它们在不同浓度情况下彼此的定量关系.

[1] Guo L. Ecology: Doing battle with the green monster of Taihu lake [J]. Science, 2007,317(5842):1166-1166.

[2] Yang M, Yu J, Li Z L, et al. Taihu Lake not to blame for Wuxi's woes [J]. Science, 2008,319(5860):158-158.

[3] 于建伟,李宗来,曹 楠,等.无锡市饮用水嗅味突发事件致嗅原因及潜在问题分析 [J]. 环境科学学报, 2007,27(11):1771-1777.

[4] Lazaro T R. Urban Hydrogy [M]. Michigan: Ann Arbor Scirnce Publishers, Inc, 1979:50-53.

[5] Rozan T F, Taillefert M, Trouwbrst R E, et al. Iron-sulfurphosphorus cycling in the sediments of a shallow coastal bay:Implications for sediment nutrient release and benthic macroalgal blooms [J]. Limnology and Oceanography, 2002,47(5):1346-1354.

[6] Shen Q S, Zhou Q L, Shang J G, et al. Beyond hypoxia:Occurrence and characteristics of black blooms due to the decomposition of the submerged plant Potamogeton crispus in a shallow lake [J]. Journal of Environmental Sciences, 2014,26(2):281-288.

[7] Watson S B, Chariton M, Rao Y R, et al. Off flavours in large water bodies: physics, chemistry and biology in synchrony [J].Water Science Technology, 2007,55(5):1-8.

[8] 陆桂华,马 倩.2009年太湖水域"湖泛"监测与分析 [J]. 湖泊科学, 2010,22(4):481-487.

[9] Lu G H, Ma Q, Zhang J H. Analysis of black water aggregation in Taihu Lake [J]. Water Science and Engineering, 2011,4(4):374-385.

[10] 邓绪伟,陶 敏,张 路,等.洞庭湖水体异味物质及其与藻类和水质的关系 [J]. 环境科学研究, 2013,26(1):16-21.

[11] 刘国锋,范成新,张 雷,等.藻源性黑水团环境效应Ⅲ:对水-沉积物界面处Fe-S-P循环的影响 [J]. 中国环境科学,2014,34(12):3199-3206.

[12] 刘国锋,何 俊,范成新,等.藻源性黑水团环境效应:对水-沉积物界面处Fe、Mn、S循环 [J]. 环境科学, 2010,31(11):2652-2660.

[13] 申秋实,范成新.藻源性湖泛水体显黑颗粒的元素形态分析与鉴定 [J]. 湖泊科学, 2015,27(4):583-590.

[14] Zhang X J, Chen C, Ding J Q, et al. The 2007water crisis in Wuxi,China: analysis of the origin [J]. Journal of Hazardous Materials,2010,182(1-3):130-135.

[15] 卢 信,冯紫艳,商景阁,等.不同有机基质诱发的水体黑臭及主要致臭物质(VOSCs)产生机制研究 [J]. 环境科学, 2012,33(9):3152-3159.

[16] 孙淑雲,古小治,张启超,等.水草腐烂引发的黑臭水体应急处置技术研究 [J]. 湖泊科学, 2016,28(3):485-493.

[17] 范成新.太湖湖泛形成研究进展与展望 [J]. 湖泊科学, 2015,27(4):553-566.

[18] 郝晓明,胡湛波,刘 成,等.南宁市竹排冲河道水体黑臭评价模型建立研究 [J]. 华东师范大学学报:自然科学版, 2011,(1):163-171.

[19] 胡荣梅,鞠 华.苏南太湖地区主要城市水环境污染综合防治研究(下) [J]. 环境科学, 1986,7(5):14-23.

[20] Canfield Jr D E, Linda S B , Hodgson L M. Relations between color and some limnological characteristics of Florida lakes [J].Journal of the American Water Resources Association, 1984,20(3):323-329.

[21] 王玉琳,汪 靓,华祖林,等.巢湖南淝河口黑水团区流速和溶解氧与Fe2+、S2-浓度的空间关联性 [J]. 湖泊科学, 2016,28(4):710-717.

[22] Seber G A F, Lee A J. Linear Regression Analysis [M]. Hoboken:Wiley, 2003:224-247.

[23] Sanford W. Applied Linear Regression [M]. Hoboken: Wiley,2005:112-124.

[24] Koenker R. Quantile Regression [M]. London: Cambridge, 2005:50-80.

[25] Cade B S, Noon B R. A Gentle introduction to quantile regression for ecologists [J]. Frontiers in Ecology and the Environment,2003,1(8):412-420.

[26] 李小平,程 曦,陈小华.淀山湖营养物输入响应关系的分位数回归分析 [J]. 中国环境科学, 2012,32(2):324-329.

[27] Chock D P, Winkler S L, Chen C. A study of the association between daily mortality and ambient air pollutant concentrations in Pittsburgh, Pennsylvania [J]. Journal of the Air and Waste Management Association, 2000,50:1481-1500.

[28] Baur D, Saisana M, Schulze N. Modeling the effects of meteorological variables on ozone concentration: A quantile regression approach [J]. Atmospheric Environment, 2004,38:4689-4699.

[29] Tang W Z, Shan B Q, Zhang H, et al. Heavy metal sources and associated risk in response to agricultural intensification in the estuarine sediments of Chaohu Lake Valley, East China [J].Journal of Hazardous Materials, 2010,176(1-3):945-951.

[30] Jin X C, Xu Q J, Huang C Z. Current status and future tendency of lake eutrophication in China [J]. Science in China Series C:Life Sciences, 2005,48(2):948-954.

[31] Shang G P, Shang J C. Spatial and temporal variations of eutrophication in western Chaohu Lake,China [J]. Environmental Monitoring and Assessment, 2007,130(1-3):99-109.

[32] Stephen B. Convex Optimization [M]. 北京:世界图书出版公司,2013:53-85.

[33] 魏复盛.水和废水监测分析方法(第四版) [M]. 北京:中国环境科学出版社, 2002:246-248.

[34] Tamura H, Goto K, Yotsuyanagi T, et al. Spectrophotometric determination of iron(II) with 1,10-phenanthroline in the presence of large amounts of iron(III) [J]. Talanta, 1974,21(4):314-318.