电容滤波型不控整流装置2/3/2/0导通模式的数值分析
2018-03-01付立军
徐 尘 付立军
(海军工程大学舰船综合电力技术国防科技重点实验室,武汉 430033)
多脉波不控整流装置因其结构简洁、运行可靠及容量大的特点在高压直流输电、变频调速系统、静止无功补偿器、有源电力滤波器等场合广泛应用[1-3]。传统上电子学对此类整流装置的研究多集中于其直流侧串接较大平波电抗器输出恒流的情形[4-6],而随着中高压变频调速系统的广泛应用,装置直流侧并联较大滤波电容作为直流电压源的情况,也在引起国内外相关学者的关注[7-11]。
根据整流装置直流侧输出电流波形是否连续,电容滤波型三相不控整流装置的工作模式可划分为电流断续模式和电流连续模式。根据工作过程中导通的功率元件数量及顺序,存在两种断续工作模式,即“2/0”模式和“2/3/2/0”模式[12]。
对长时间稳态工作的整流装置,一般应确保其处于电流连续模式,避免电流断续带来较大谐波畸变。但若装置工作在某些负载变化较快的场合,如脉冲负载,则不可避免出现电流断续。由于2/3/2/0模式状态间切换过程复杂,在 1/6周期内会出现 4种电路模态,且其相对应的负载范围窄,因此以往对于整流装置断续模式的研究集中于2/0模式[13-17],忽略了对2/3/2/0模式的研究。如果采用2/0模式的计算方法来近似计算2/3/2/0模式,则不可避免会出现计算偏差。因此,完善2/3/2/0模式的研究,对准确分析电容滤波型三相不控整流装置的非线性运行机理具有现实意义。对完善多脉波不控整流装置(如12脉波、24脉波)的运行模式研究也有借鉴参考价值。
本文采用经典电路分析方法,分析了2/3/2/0模式4个导通阶段间的边界条件,利用电路的对称性对不同导通状态下电容滤波型三相不控整流装置的电压电流参数建立了微分方程,应用数值计算方法最终求得精确解,经过与电路时域仿真相比对,最终证明该方法的准确性。
1 2/3/2/0模式的等效电路
电容滤波型多脉波不控整流装置交流侧大多连接变压器或发电机,交流电感的作用不可忽略,而由于空间、成本约束,直流侧一般不再专门配备滤波电感,而并联以较大容量的滤波电容。如图1所示,L为交流侧等效电感,r为交流侧等效电阻,C为滤波电容,R为负载电阻。本文中设电路参数对称,交流侧为理想的三相交流电源,不含高次谐波。由图2交流电流波形可知,2/0模式分为二管导通和电流断续两个阶段。2/3/2/0模式则分4个阶段:①二管导通,为方便叙述,以D1、D6管起始导通为例,作为整个过程的起点;②发生换相,由于线电压周期脉动,存在由 A、B相换至 A、C相的过程。而换相过程中由于交流电感的存在导致电流无法突变,会出现D1、D2、D6三管导通;③换相结束,再次进入二管导通,但时间很短,此时D1、D2导通;④换相过后出现交流侧电流断续,此时电流为0,直到出现新的二管导通为止。整个过程持续π/3电角度。
设[0, γ]为 D1/D6管导通区间,[γ, δ]为 D1/D2/D6管导通区间,[δ, ε]为 D1/D2导通区间,[ε, π/3]为无器件导通区间。对不同区间的直流电压uc和交流电流iA、iB、iC进行划分,4个阶段分别用下标1、2、3、4加以区分。其各个阶段的等效电路如图3所示。
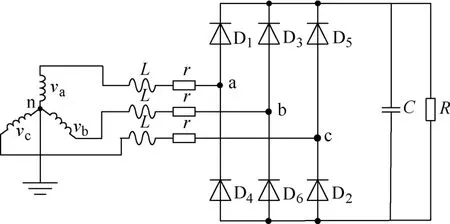
图1 电容滤波型三相不控整流装置拓扑
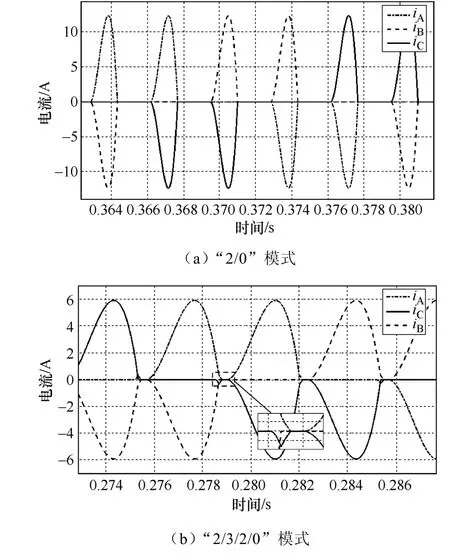
图2 电容滤波型三相不控整流装置的电流断续模式交流电流波形
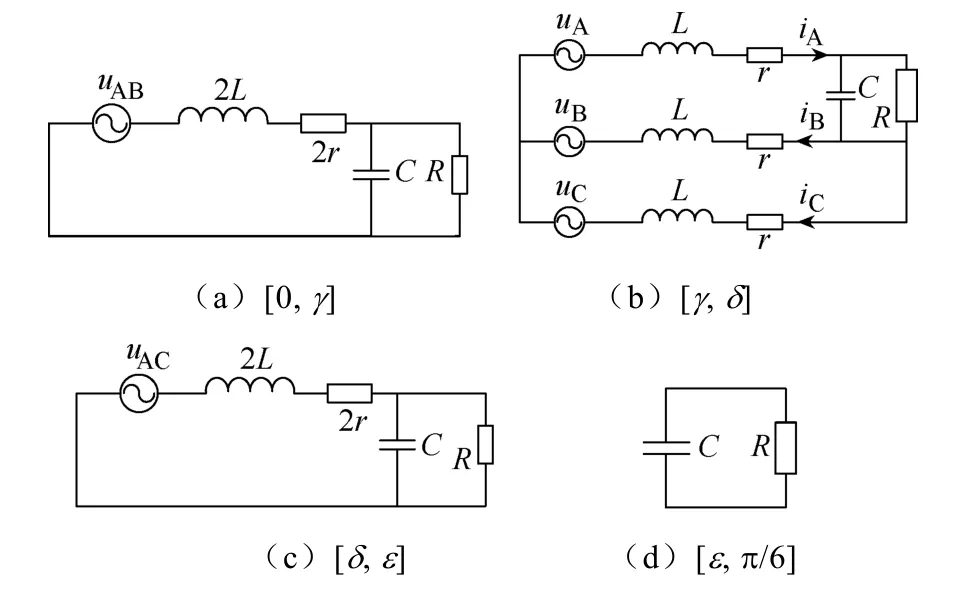
图3 2/3/2/0模式的等效电路
2 2/3/2/0模式的数值分析
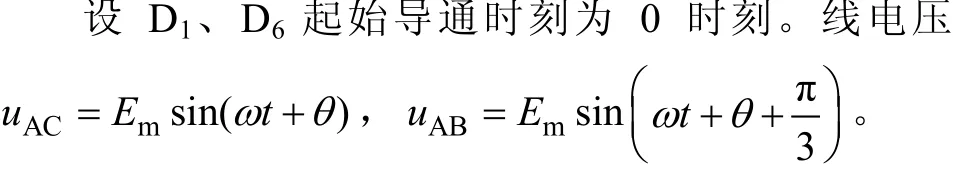
在第一个二管导通区间,结合基尔霍夫定律,有如下二阶微分方程:
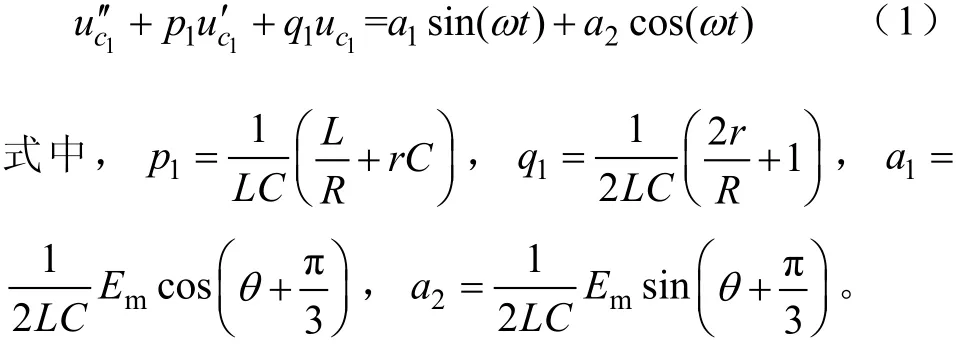
当式(1)的特征方程具有共轭复根时,该方程解的形式为

但是c1仍未知,留到后文解决。
0时刻交流电流为0,变化率也为0,有如下关系:
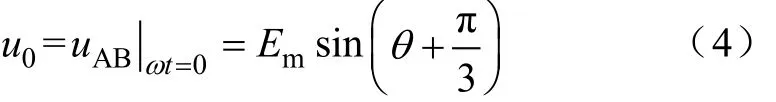
由式(4)可知,u0为变量θ的函数。
tωγ=时刻,第一次二管导通结束,进入三管导通阶段,D1/D2/D6管导通,此时,iB=iA,C相电流iC为0,其电流变化率也为0,其等效电路如图4所示,并可以建立如下方程组:
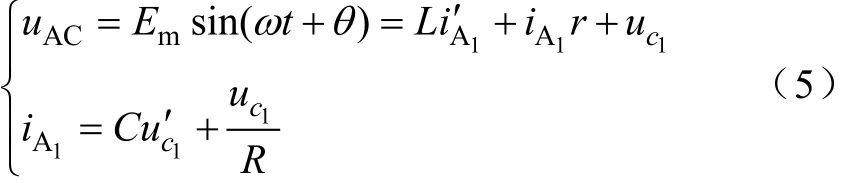
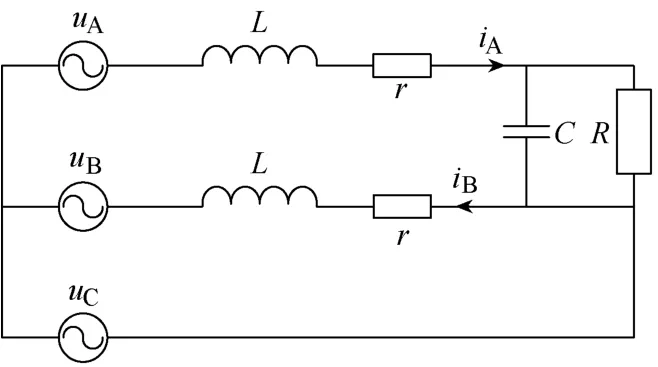
图4 三管导通起始时刻等效电路
则有
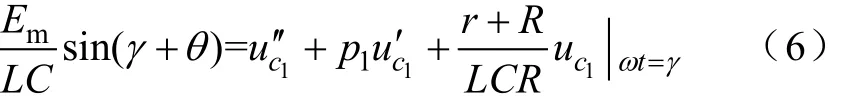

式(7)的第一个方程为二阶非齐次常微分方程,当该二阶方程的特征方程具有共轭复根时,uc2的解可表示为


进入[δ, ε]区间的等效电路,整流装置再度进入二管导通状态,类似方程(1),可得直流侧电容电压3cu 的二阶微分方程如下(方程中ωt取[0, ε−δ]):

由ε时刻电流断续,电路开路,得到临界条件:

此时直流电压与线电压有如下关系:
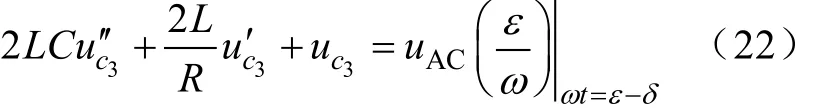
而设电流断续时的电容电压等于u3,有如下表达:
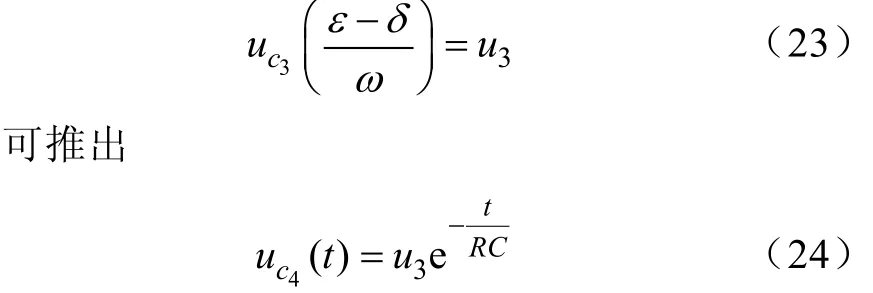
由式(27)可知,可将c1看做u4的函数,而式(26)的后半式u4可由u3表达。这样,前文假设的其他参数 u1、i1、u2、i2、u4均可由 5个未知数θ、γ 、δ 、ε 、u3的相关函数来表示。这5个未知数,由式(6)、式(15)、式(21)、式(23)、式(25)组成非线性方程组,采用数值计算方法如牛顿法、割线法等,可求出上述5个未知数的确定解,应注意上述数值计算法均为局部最优解法,所以初值选取应尽可能合理。求出相关未知数后,可根据式(27)求出直流电压uc,uc呈现6倍频波动。
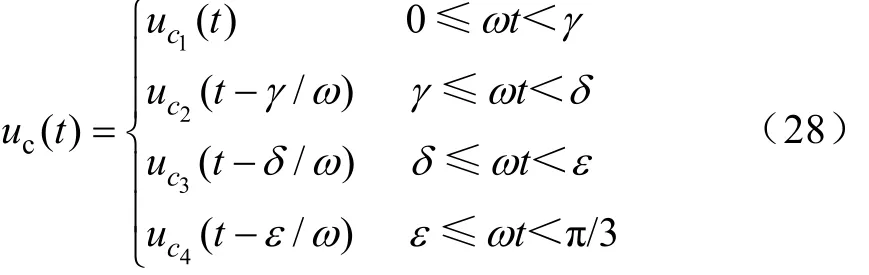
直流电流 id在区间[0, π/3]内与 A 相电流 iA重叠,也呈现6倍频波动。表达式如式(28)所示。
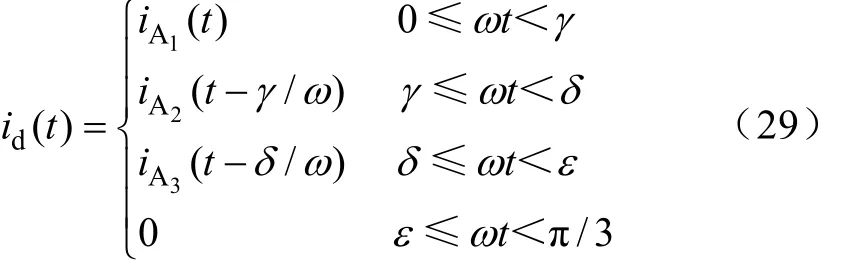
以A相电流为例,2/3/2/0导通模式下的半个周期内交流侧电流表达式如式(29)所示,由于交流电流存在半波对称的特点,所以后半周期(t)=−iA(t − π /ω)。
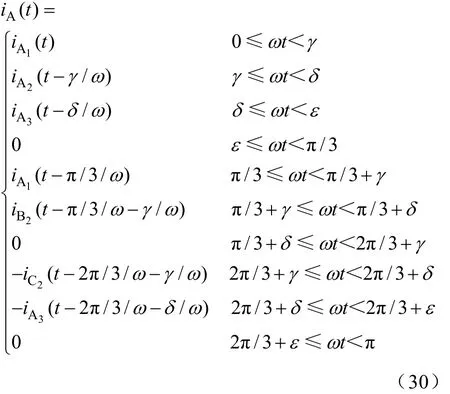
3 初值选取及算法收敛性
本文提出的对非线性方程的数值求解,传统多采用牛顿法、二分法、割线法或其他改进型算法。这类迭代法一般都有局部收敛的问题,因此,初值的选择对于算法最终是否能够收敛十分关键,初值的选取应尽量接近。本文对初值的选取原则如下:2/3/2/0导通模式介于 2/0导通模式和 3/2导通模式之间,三管导通时长很短,可近似将γδε、、都取为π/3;θ为线电压 uAC与D1、D6起始导通时刻的差值,由于交流电感引起二极管导通延迟,所以这个角度应选择在0到π/6之间,本文取为π/12;而电压u3的初值可由不控整流的直流电压平均值的计算公式[5]近似得到,近似取为1.35m/E 。
4 仿真与验证
利用符号计算软件 Mathematica对上述方程组进行编程,调用该软件的FindRoot函数,选择割线法对上述5个方程进行数值求解。计算算例参数如下:L=0.2mH,r=0.02Ω,C=3.3mF,R=8.5Ω,Em=2206V,交流电压频率为 50Hz。装置工作在稳态时,处于2/3/2/0模式。同时利用Matlab/Simulink软件对如图1所示电路进行时域仿真,仿真中设定二极管为理想开关元件,未考虑导通压降,以验证本文提出的计算方法。计算经过8次迭代收敛,数值计算求解方程组结果见表1。

表1 计算结果
由式(33)、式(34),通过分别计算电容电压uc及直流电流 id在π/3电角度内的傅里叶级数求取各特征频率幅值,获得各次谐波含量;在时域仿真中则通过使用Powergui模块的FFT分析工具获得电容电压及直流电流的谐波分量。计算结果与仿真对比见表2至表4。
从表 2、表 3中可以看出,直流侧的谐波分量主要为6次谐波的倍频分量。由表4可知,交流电流谐波次数为6n±1次。计算结果、仿真结果的直流分量和各次谐波幅值基本一致,证明了本文所提方法的正确性。
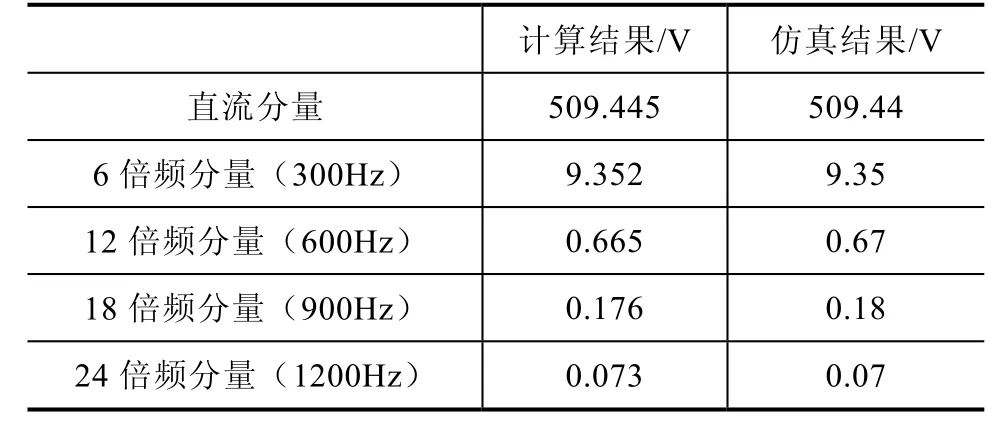
表2 直流电压谐波含量计算结果与仿真结果对比
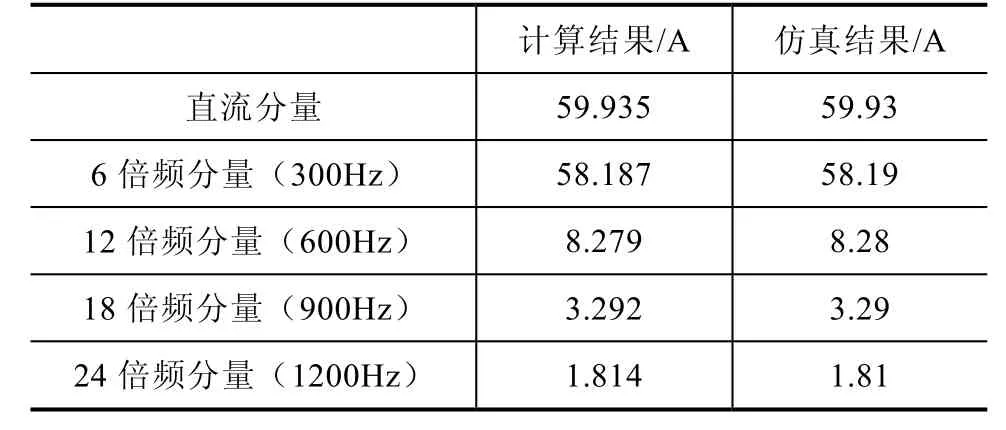
表3 直流电流谐波含量计算结果与仿真结果对比
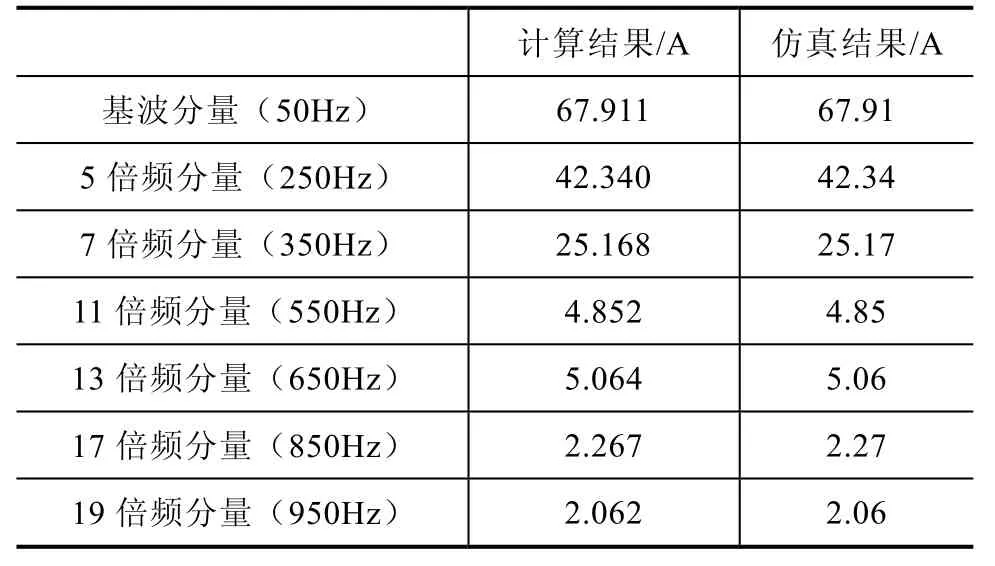
表4 交流电流谐波含量计算结果与仿真结果对比
5 结论
对三相不控整流装置的电流断续模式,以往的研究基本上聚焦于“2/0”模式。对切换状态复杂的“2/3/2/0”导通模式,在三相对称且交流电压不含高次谐波分量前提下,本文进行了分析计算方法的推导。主要根据不同导通状态的分界条件,利用电路的对称性,列写出解析表达式。最终将复杂的电路状态转换用五元微分方程组来表达,继而利用数值计算方法,求解了该超越方程组。本文利用上述方法分析了电压、电流的谐波含量,与仿真对比,验证了该方法的正确性。
[1] 孙宇光, 黄子果, 陈丽, 等. 十二相整流同步发电机定子匝间短路故障计算[J]. 电工技术学报, 2014,29(3): 57-64.
[2] 王佳佳, 周念成, 王强钢, 等. 电网电压不平衡下串联型12脉波整流装置的频域谐波建模[J]. 电工技术学报, 2015, 30(5): 69-78.
[3] 于洪乾, 张俊华, 马会茹, 等. 同步电动机旋转整流器故障分析与处理[J]. 电气技术, 2015, 16(9):106-108.
[4] 王兆安, 刘进军. 电力电子技术[M]. 5版. 北京: 机械工业出版社, 2009.
[5] 陈坚, 康勇, 阮新波, 等. 电力电子学: 电力电子变换和控制技术[M]. 北京: 高等教育出版社, 2011.
[6] Kimbark E W. Direct current transmission[M]. John Wiley & Sons, 1971.
[7] 王兆安, 杨君, 刘进军, 等. 谐波抑制和无功功率补偿[M]. 北京: 机械工业出版社, 1998.
[8] 徐德鸿, 马皓, 汪槱生. 电力电子技术[M]. 北京:科学出版社, 2007.
[9] Sudhoff S D, Wasynczuk O. Analysis and averagevalue modeling of line-commutated convertersynchronous machine systems[J]. IEEE Transactions on Energy Conversion, 1993, 8(1): 92-99.
[10] Sudhoff S D, Corzine K A, Hegner H J, et al. Transient and dynamic average-value modeling of synchronous machine fed load-commutated converters[J]. IEEE Transactions on Energy Conversion, 1996, 11(3):508-514.
[11] 孙媛媛, 李佳奇, 尹志明, 等. 含不控整流的交-直-交变换器频域谐波分析模型[J]. 中国电机工程学报,2015, 35(21): 5483-5491.
[12] Hancock M. Rectifier action with constant load voltage:Infinite-Capacitance condition[C]// Proceedings of the Institution of Electrical Engineers, 120. 12, 1973:1529-1530.
[13] 马凡, 马伟明, 付立军, 等. 直流侧电流断续时不控整流器的动态小信号数学模型建立与验证[J]. 中国电机工程学报, 2010(9): 40-46.
[14] 马凡, 马伟明, 付立军, 等. 直流侧电流断续时不控整流器的动态大信号数学模型建立与验证[J]. 中国电机工程学报, 2010(12): 36-42.
[15] 李佳奇. 三相电压型不控整流装置的频域谐波模型[D]. 济南: 山东大学, 2015.
[16] 孙媛媛. 非线性电力电子装置的谐波源模型及其在谐波分析中的应用[D]. 济南: 山东大学, 2009.
[17] Carpinelli G, Iacovone F, Russo A, et al. Analytical modeling for harmonic analysis of line current of VSI-fed drives[J]. IEEE Transactions on Power Delivery,2004, 19(3): 1212-1224.
