进给伺服系统的PID参数整定

文思奇 林荣文 黄李威

（福州大学电气工程与自动化学院，福州 350108）

在交流伺服系统中，多数采用三相永磁同步电动机（PMSM）。这类电动机与无刷直流电动机（BLDC）和感应异步电动机（IM）相比，其效率高，运行可靠。永磁同步电动机有两种类型，一种是内装式，另一种是外装式。外装式常见的隐极式同步电动机，其特点是在d轴和q轴上，磁路的磁阻基本相同。内装式常见的凸极式同步电动机[1]，其特点是在q轴上的磁阻小于d轴，且结构简单，制造成本低，易对永磁磁极进行优化设计[2]。

目前在工业上大量使用常规的PID参数调节来实现控制伺服系统，这种固定参数的调节方式由于系统的非线性和被控对象特性变化时，控制性能比较差。于是可以借助智能控制算法来达到更好的控制效果。

本文主要介绍基于遗传算法的伺服系统PID参数整定，通过Matlab仿真Kp、Ki、Kd参数自整定得到最优解。

1 数控机床进给伺服系统的数学模型

1.1 PMSM的数学模型

通过坐标变换将三相坐标系下的定子交流电流变换为两相旋转坐标系下的直轴电流和交轴电流[3]。

为了得到理想情况：①假设磁路不饱和；②定子三相绕组对称，忽略空间高次谐波；③忽略铁心损耗（涡流损耗和磁滞损耗）；④定子空载电动势是比较标准的正弦波；⑥系统中频率和温度对绕组的电阻假设无影响，一直保持恒定值。图1为PMSM等效结构坐标图。

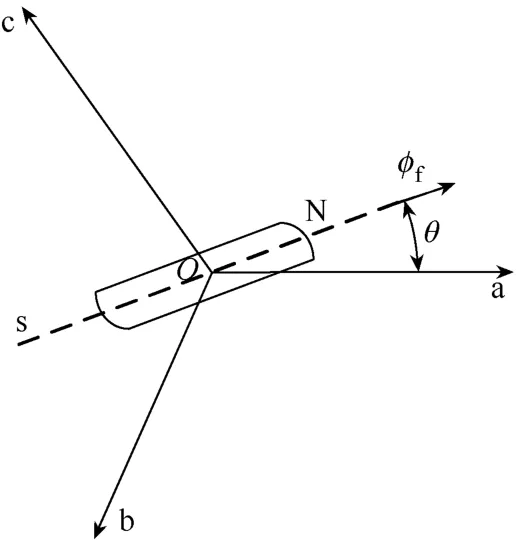
图1 PMSM等效结构坐标图

图1 中，Oa、Ob、Oc为三相定子绕组的轴线，取转子的轴线与定子a相绕组的轴线的电气角为θ，可以建立永磁同步电动机的物理方程[4]为

式（1）、式（2）分别是感应电动机的电压方程和磁链方程，ua、ub、uc是三相定子绕组的电压，ia、ib、ic是三相定子绕组的电流，ϕa、ϕb、ϕc是三相定子绕组的磁链，定子电阻Ra＝Rb＝Rc＝R，定子电感La＝Lb＝Lc=L；ϕf为转子磁场的等效磁链。

三相定子交流电的主要作用是产生一个旋转的磁场[5]，当两相相位正交的对称绕组通以两相相位相差90°的交流电时，也能产生旋转磁场。根据矢量变换原理，建立一个与永磁同步电动机转子同步旋转的d-q坐标系，让d轴与转子磁极重合，顺着旋转方向超前90°电角度为q轴，把永磁同步电动机定子的各参量都转化到d-q旋转坐标系下。

1.2 矢量变换原理

矢量变换分为Clarke和Park两种，变换的基本的原则是变换前后磁动势完全等效。矢量变换时，先进行 Clarke变换，式（3）中将三相静止坐标系的电流值iA、iB、iC转换为两相静止坐标系中的电流值 iα、iβ。然后再经过 Park变换，两相静止坐标系就变成了两相旋转坐标系[6]。式（5）中将两相旋转坐标系中的电流值 iα、iβ转换为两相静止坐标系中的电流值id、iq。

图2为OABC到Oab的转换。

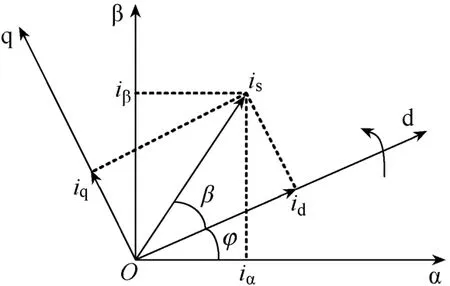
图2 OABC到Oαβ的转换

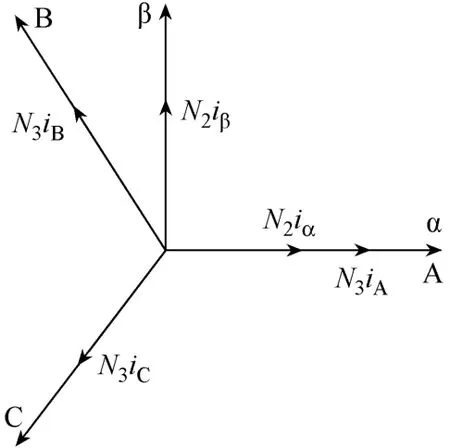
图3 Oαβ到OMT的转换

可以得到Clarke正变换为

Clarke和Park变换其用意就是将交流电动机电流解耦成励磁电流跟电驱电流来控制，模拟直流电动机一样的控制特性。

1.3 同步旋转坐标上的PMSM数学模型

凸极式电动机的自感互感都是余弦函数，将电压方程变成含有时变系数的微分方程。图4为永磁同步电动机矢量图。

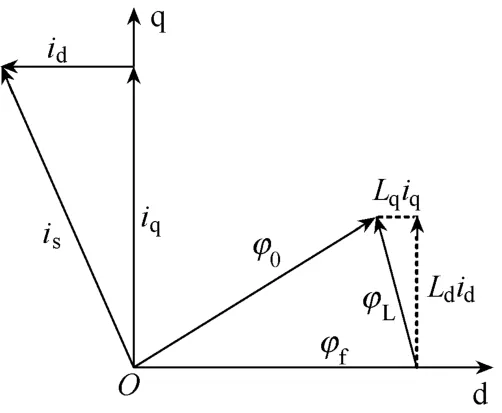
图4 永磁同步电动机矢量图

设定Lmd、Lmq为d、q轴的励磁电感；Lsσ为d、q轴线圈的漏感；ud、uq为d、q轴定子电压；id、iq为 d、q轴定子电流；φd、φq为 d、q轴定子磁链；Lq=Lmq+Lsσ、Ld=Lmd+Lsσ为 d、q 轴的总电感；φf是转子磁场的等效磁链。

得到PMSM电流方程为

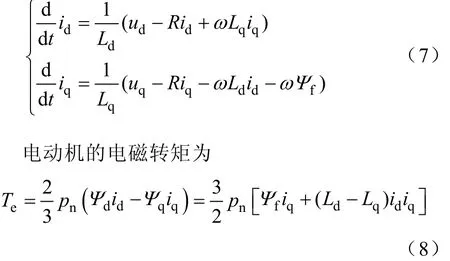
2 遗传算法在PID控制中的应用

遗传算法（genetic algorithms, GA）是以自然选择和基因遗传理论为基础[7]，模拟大自然生物进化过程，通过选择，交叉，变异等操作[8]，在解空间中通过指定的迭代次数进行寻优，向着全局最优的方向收敛。

在遗传算法中，根据实际需求设定一个适应度函数，筛选出适应度较高个体，以提高遗传算法的搜索效率和全局搜索能力[9]。遗传算法过程用到了适应度准则，适应度高的会拥有较高概率遗传到下一代中，适应度低的则会拥有较高的概率被淘汰[10]。

选用误差绝对值时间积分性能指标作为参数选择的最小目标函数，即

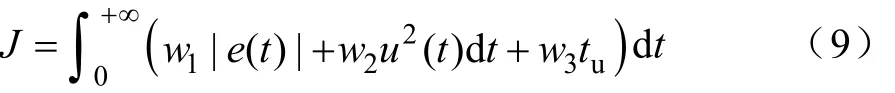
式中，e(t)为系统误差；u(t)为控制器输出；tu为上升时间；w1、w2、w3、w4为权值，而且 w4＞＞w1。

本文取适应度函数为目标函数J的倒数，即

式中，遗传算法在进化搜索中基本不利用外部信息，仅以适应度函数为依据，利用种群每个个体的适应度来进行搜索。因为适应度函数的复杂度是遗传算法复杂度的主要组成部分，所以适应度函数的设计应尽可能简单，使计算的时间复杂度最小。

在伺服系统中应用遗传算法时，首先需要对参数进行编码和译码操作。编码一般有二进制编码和浮点数编码两种方式，这里选用二进制编码。由于二进制编码不能直接在控制器算式中使用，因此必须解码后使用。编码时，将3个参数分别代表10位二进制码，同样在解码过程中，将这个数字串分为三部分，每十位为一个二进制编码。然后转换成十进制数。例如在工业过程控制中，Kp的变化范围是从0.1到100。Kp译码公式如下：

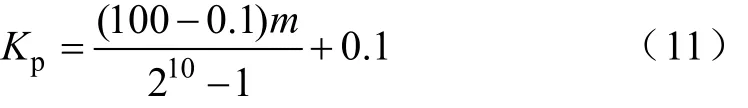
式中，m为十位无符号二进制编码。

再确定一个解码方案，相当于基因型到表现型的转换。然后进行解码操作。再通过已经确定的转换规则可得到个体的适应度。适应度值非负，适应度值增加的方向就是目标函数优化的方向。图5为基于遗传算法的PID优化控制方案原理图。

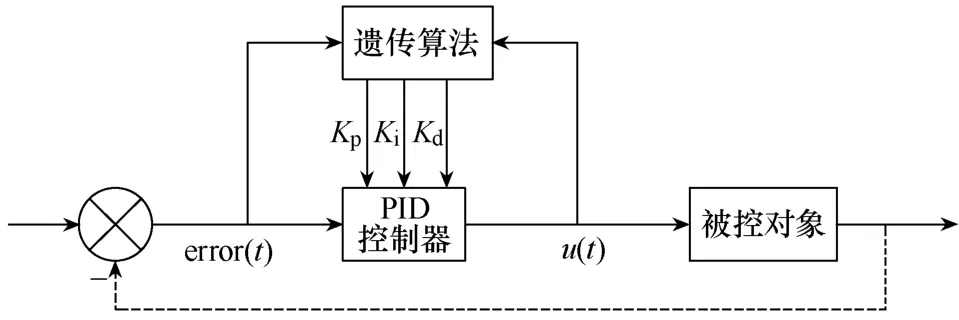
图5 基于遗传算法的PID优化控制方案原理图

本文选用比例选择算子。因为比例选择算子严格的遵循个体被选中的概率和适应度呈线性的正比关系。

式中，Pi代表被选中的概率。在这个群体中适应度高的个体要比适应度低的个体更容易遗传下去，因为被选中进行复制的概率大。这样就使得这种遗传关系变得特别容易从适应度中看出来，并且比较标准。

根据遗传算法的流程，可以得到基于遗传算法的PID参数寻优的流程图。与单纯的GA算法类似，也是一个迭代循环。

图6是基于遗传算法的PID整定流程图，可以看出在经过主要的选择变异交叉操作后，进行判断，若群体不稳定，则继续迭代；若达到稳定条件，则停止操作，输出寻优结果。

这种算法方法简单，仅仅需要对数字串进行复制交换或者改变某一位。由于复制、交叉和变异功能以及群点寻优的方式避免了陷入局部最优解问题，所以这种方法不受模型初始条件的影响，可以在完全不知道系统初始状态的情况下，在一个解空间中进行迭代寻优。一般来说，先根据传统工业控制中的实际操作经验，选取一组参数，然后进行遗传算法的迭代，直到达到控制要求为止。这样就可以节省很多时间以及避免不必要的时间浪费以及计算浪费，提高了控制效率。

把遗传算法运用于PID的参数整定，不但克服了常规PID整定方法的缺点，而且实现了PID参数离线整定。这种方法把遗传学的思想与控制工程相结合，模拟自然进化过程，搜寻最优解。

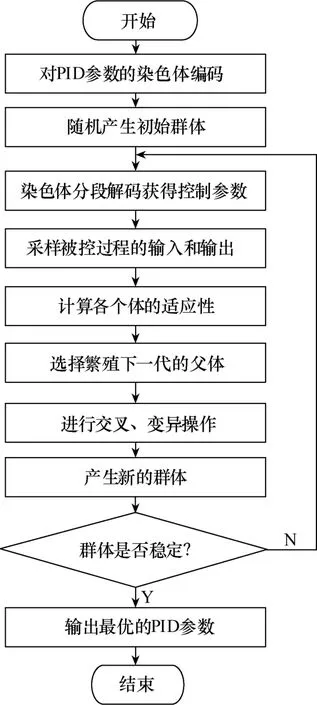
图6 遗传算法（GA）流程

3 进行Matlab仿真

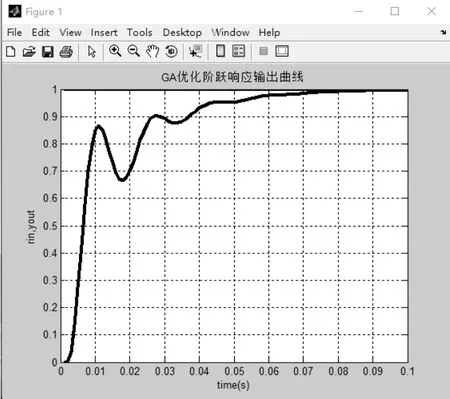
图7 阶跃响应输出曲线

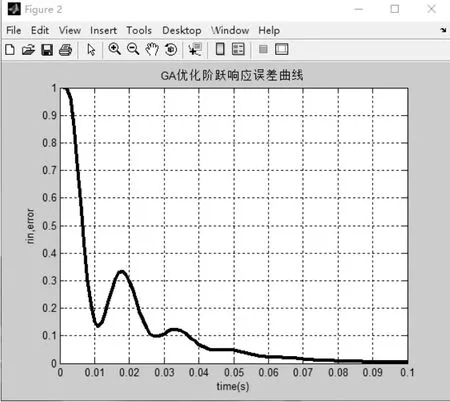
图8 阶跃响应误差曲线

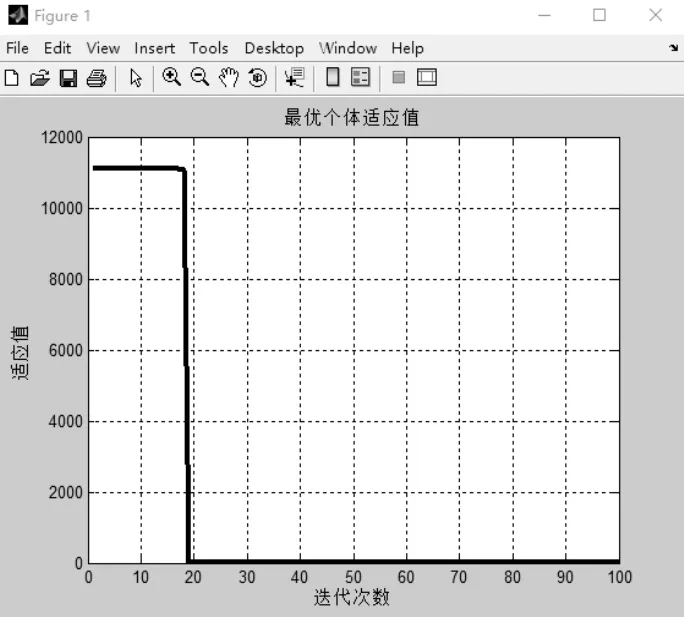
图9 最优个体适应值

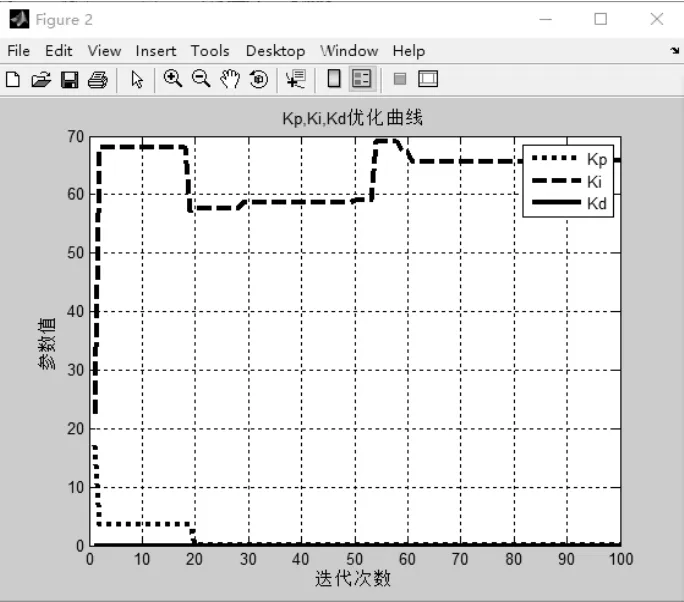
图 10 Kp、Ki、Kd优化曲线

使用经验法选定Kp、Ki、Kd参数时，假设选定的Kp=0.5、Ki=60、Kd=0，当输入为一阶跃函数时，得到输出曲线和误差曲线，分别如图7和图8所示。

图7中调节时间为0.071s，很明显能看出此次调节时间较长，且系统波动较大。若应用在实际的工业控制中，控制效果不太好。使用遗传算法时，进行Matlab仿真。

其中，Kp=0.1656、Ki=65.8216、Kd=0，适应度函数的最优值是Jbest=11.64。可以看出在100次迭代中，最优个体适应度值在 20次循环后逐渐趋于稳定。在图10中，采样点取每次迭代的最后一次结果，也就是最优解，采样100次后，绘制出优化曲线图。可以看出得到Kp、Ki、Kd都已经稳定，取出这个稳定值就是最优解。Kp、Ki、Kd得到最优解后绘制输出曲线和误差曲线，分别如图11和图12所示。

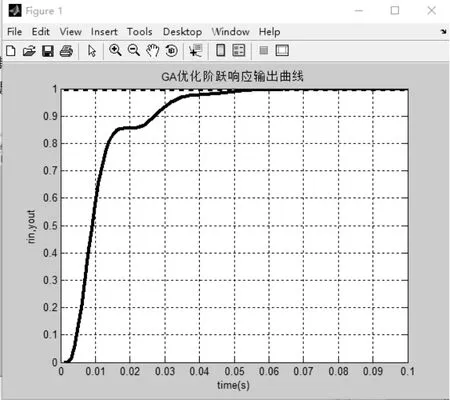
图11 GA优化阶跃响应输出曲线

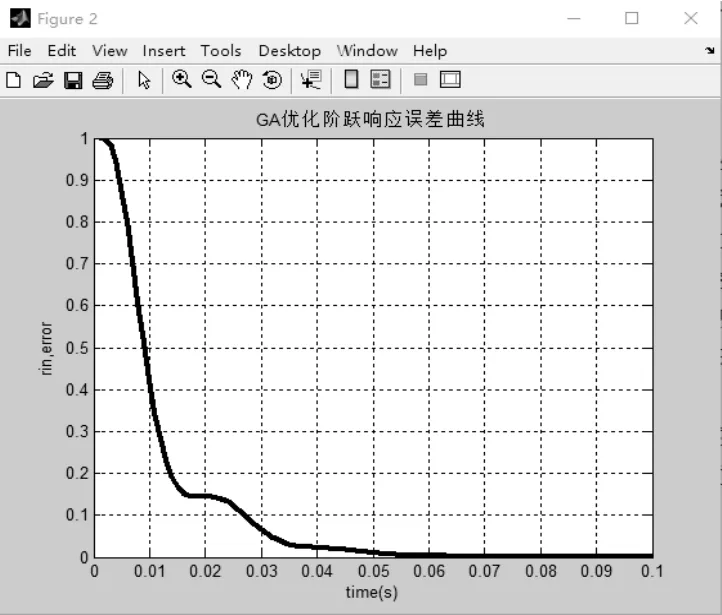
图12 GA优化阶跃响应误差曲线

调节时间为0.0481s，相比于使用经验法，调节时间已经明显变短，图形波动也没有经验法变化的剧烈，波形更加平滑。因此，可以知道基于遗传算法的PID参数调节比仅仅依靠经验值进行估算Kp、Ki、Kd的方式收敛速度更快。

4 结论

通过本文的研究，传统的PID控制依靠经验选取参数，曲线波动较大，调节时间也比较长。相比于传统的PID控制，基于遗传算法的PID控制效果更好，实现了PID参数调节的全局最优化。经过仿真实验，可以得出基于遗传算法的PID参数整定与传统的PID参数选定相对比，具有更加精确的优点，多目标寻优，运算速度更快，鲁棒性强，是理想快捷的优化算法。

[1] 陈坚. 交流电机数学模型及调速系统[M]. 北京: 国防工业出版社, 1989.

[2] 陈修亮, 车倍凯. 永磁同步电机矢量控制解耦方法的研究[J]. 电气技术, 2013, 14(4): 37-40, 43.

[3] 廖效果. 数控技术[M]. 武汉: 湖北科学技术出版社,2000.

[4] 邱丽, 曾贵娥, 朱学峰. 几种PID控制器参数整定方法的比较研究[J]. 自动化技术与应用, 2005, 24(11):28-31.

[5] 夏加宽, 王桐. 一种新颖的不对称六相 SVPWM 算法[J]. 电气技术, 2014, 15(2): 9-13, 19.

[6] 胡金高, 程国扬. 鲁棒近似时间最优控制及其在电机伺服系统的应用[J]. 电工技术学报, 2014, 29(7):163-172.

[7] 左月飞, 张捷, 刘闯, 等. 基于自抗扰控制的永磁同步电机位置伺服系统一体化设计[J]. 电工技术学报,2016, 31(11): 51-58.

[8] 肖曦, 许青松, 王雅婷, 等. 基于遗传算法的内埋式永磁同步电机参数辨识方法[J]. 电工技术学报,2014, 29(3): 21-26.

[9] 张晓楠, 方浩, 戴冠. 遗传算法的编码机制研究[J].信息与控制, 1997, 26(2): 134-139.

[10] 郭庆鼎, 李蒙, 郭威. PID控制器参数的遗传算法优化设计[J]. 沈阳工业大学学报, 2000, 22(1): 31-33.