基于改进Q学习算法的储能系统实时优化决策研究

汪 波 郑文迪

（福州大学电气工程与自动化学院，福州 350116）

储能系统具有平衡功率波动，对负荷曲线削峰填谷的优点，也可以提高分布式设备的利用率，节省分布式电源容量成本，还可以保持系统稳定[1-5]。中关村储能产业技术联盟发布的《储能产业研究白皮书 2016》预测，到 2020年，理想情景下，我国储能市场总装机规模将达 24.2GW；常规情景下，我国储能市场总装机规模也将达到 14.5GW。随着分布式能源近年来大规模接入电网，其作用更加重要，而储能投资成本近年来也不断下降，储能产业将快速发展并推动能源变革。

目前，储能系统的运行主要面临两个问题：①绝大部分的储能系统控制策略都是将其作为辅助元件，被动的接收调度命令，如文献[6]提出一种消纳高渗透分布式光伏发电有功功率波动的集中式储能电站实时调度方法。文献[7]在孤岛运行微电网能量优化管理中，不仅对分布式发电输出功率进行优化分配，还根据模糊逻辑对蓄电池的充放电进行能量的调度。文献[8]将蓄电池虚拟放电和充电价格计入群体寻优目标函数，结合协同进化遗传算法，使用群体寻优目标函数和精英寻优目标函数寻求分阶段经济调度最优解。在这种情况下，当电力用户和中间商都参与进来的时候，调度需要考虑太多因素，不满足实时调度的实时性需求。②目前的储能系统充放电策略优化算法有遗传算法[9]、粒子群算法[10]、模拟退火算法[11]、动态规划算法[12]等，这些方法都是针对负荷曲线为确定情况，而在实时调度期间，实时负荷功率与预测值有误差，以上方法都需要重新计算策略，不满足实时性需求。文献[13]研究了储能系统能量调度及需求响应联合优化问题，对储能单元动作及可延时负荷动作进行优化控制，但是其并没有量化储能系统的充放电数值，而且其采用的传统Q学习算法，收敛速度较慢，需要调整好参数才能收敛。

本文使储能系统以净负荷功率曲线方差最小为目标，决策其每一实时调度周期的充放电功率值。提出了用全局最优惩罚项的方法来引导Q学习算法获得一天的最优动作值，相比于传统Q学习算法，收敛速度更快；用训练好的Q值表指导储能系统在实时调度周期做出最优充放电动作决策，在净负荷功率预测不准确的情况下不需要重新迭代运算获得最优动作值，从而满足实时性要求。

1 优化模型

储能系统拥有者不同，其目标函数也会不一样,本文研究对象是电网投资建设的储能系统，其目的是使净负荷功率曲线更加平坦，而方差可以反映曲线的平坦程度，因此其目标函数为

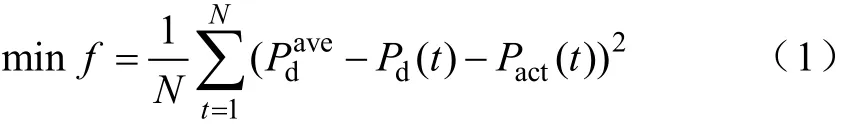
式中，Pd(t)为负荷功率；Pact(t)为储能系统吸收功率决策值，当Pact＞0时，表示储能系统吸收功率，当Pact＜0时，表示储能系统释放功率，净负荷功率为负荷功率加上储能系统吸收功率决策值；为一天的负荷功率平均值；N为一天总的实时调度周期数，每一个实时调度周期时间间隔为1440/N分钟；t为实时调度周期数。

储能系统在致力于使目标函数最优时，自身限制和算法需要存在如下一些约束条件。

1）存储电量约束

储能系统能够存储的电量值是一定的，其最小值为Emin，最大值为Emax，即

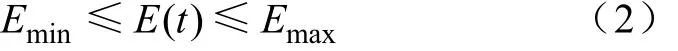
储能系统在循环充放电过程中，其存储电量不能超过其限值，否则会损害其寿命。

2）末时段存储电量约束

为了使储能系统工作周期为一天持续进行，每天初始实时调度周期和末端实时调度周期的存储电量需相等

这样，储能系统的充放电策略就不会影响一天的负荷功率平均值。当 t调度周期储能系统存储电量E(t)大于末时段要求E0时，假设一天中剩余调度周期可释放功率的调度周期数为m1，如果

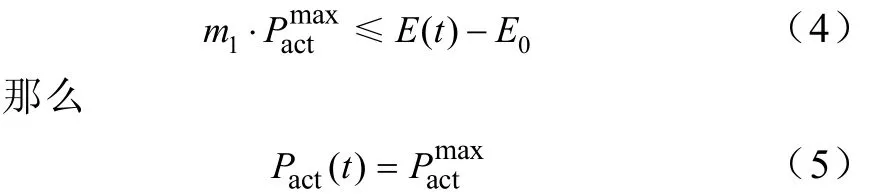
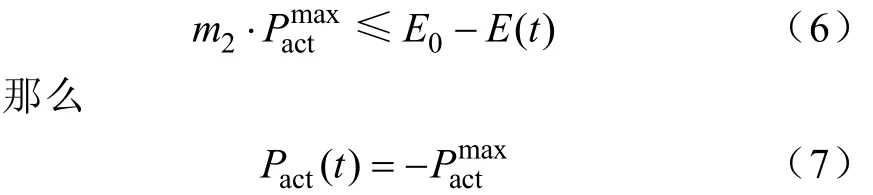
3）充放电动作约束

储能系统受爬坡速率约束，其充放电动作值不能超过其充电功率最大值

如果负荷功率预测是准确的，那么大部分的寻优算法都可以得出储能系统在一天的充放电最优值，但是实际情况下负荷预测是不准确的，提前一天的短时预测值与实时调度周期的实际值会存在误差，而实时调度周期时间间隔短，无记忆功能的寻优算法在实时调度周期需要重新计算最优动作值，不满足实时性要求。本文提出改进的Q学习算法，可以将训练好的Q值表用于储能系统在实时调度周期快速做充放电决策。

2 Q学习算法

2.1 传统Q学习算法

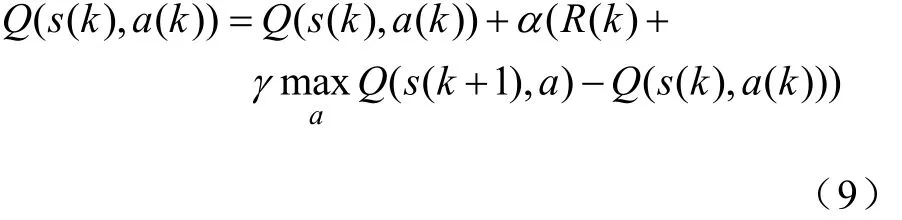
Q学习算法适用于解决含不确定性的控制问题，且算法执行效率与模型的复杂程度相关性较小。Q学习算法基本形式为式中，k为迭代次数；Q(s(k), a(k))表示s(k)状态采取a(k)动作后得到的Q值；α为学习率；R(k)为即时报酬；γ为遗忘因子，采取a(k)动作后得到s(k+1)状态；Q(s(k+1),a)为 s(k+1)状态采取所有可能动作 a后得到的所有Q值。

2.2 改进Q学习算法

传统的Q学习算法需要调整学习率和遗忘因子两个参数，其最优解的获得是通过一定概率选取不同动作看是否使总收益增大，这种方法在迭代中可能得到较优的策略，但是也有可能得到较差的策略，具有较大的偶然性，学习速度慢，迭代次数较多，而且其参数的选取对得到最优值的迭代次数具有较大影响，当参数选取不合适甚至可能得不到最优解。

基于Q值表的记忆功能，本文提出去掉遗忘因子项，取0γ=，即得到的即时报酬只是反映单个状态下采取单个动作可以获得的报酬值，它们之间的关系是解耦的，用离线数据学习训练后可以得到一个初始Q值表，再引入全局优化惩罚项Rc，基于训练好的初始Q值表，用全局优化惩罚项引导算法收敛，获得整个过程的最优动作策略，改进后的Q学习算法基本形式变为

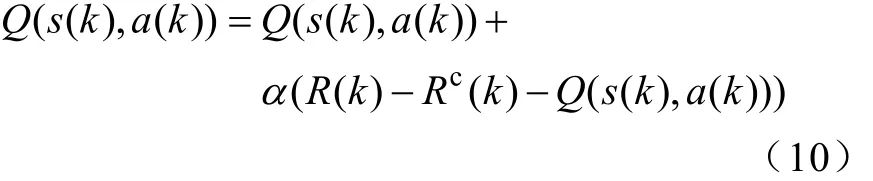
3 储能系统Q学习模型

3.1 全局优化惩罚项设计

由于本文所提改进算法是利用全局优化惩罚项来引导其收敛，所以改进算法的关键是设计好全局优化惩罚项。将改进算法应用到储能系统，基于附录A推导，考虑到储能系统充放电功率大小有约束，并且充放电动作值采用的是离散值，本文提出惩罚判据项为

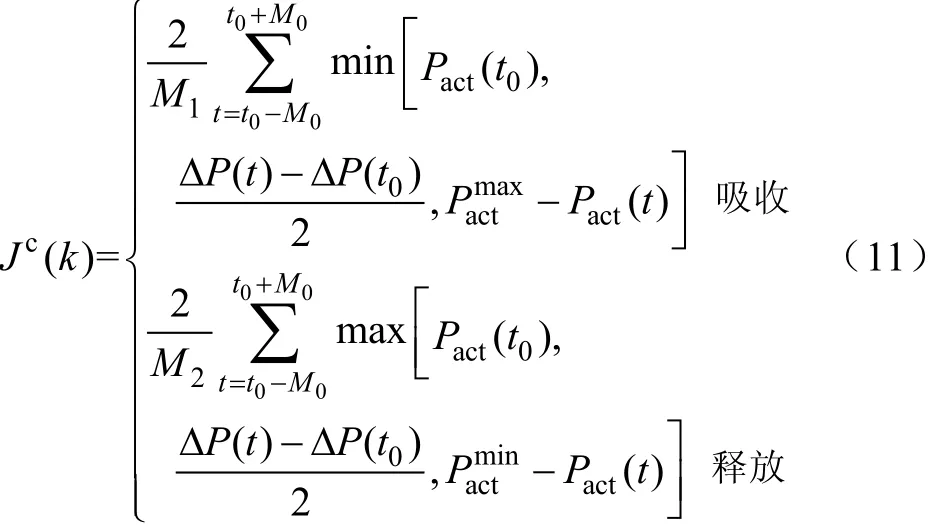
式中，Δ P (t) = P (t) + a (t) −，M0为t0调度周期所d 在峰谷时段调度周期个数的一半；M1为(M0−t0)到(M0+t0)调度周期中 Δ P(t) ＞ ΔP(t0)的调度周期个数；M2为(M0−t0)到(M0+t0)调度周期中 Δ P(t) ＜ ΔP(t0)的调度周期个数。为储能系统充电功率动作值最大值，为储能系统充电功率动作值最小值，即放电功率最大值。

基于惩罚判据项，动作值为吸收功率时全局优化惩罚项为

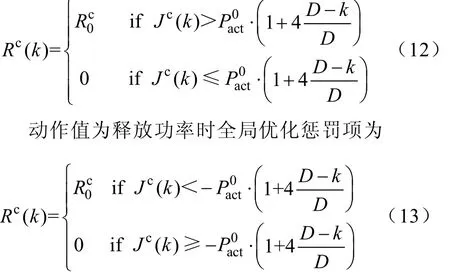
3.2 状态空间集合

储能系统在进行充放电决策之前需要先判断其所处状态空间。将实时调度周期 t、实时负荷功率Pd(t)、峰谷时段负荷功率最值与平均值差值的绝对值、峰谷时段剩余所需负荷功率和储能系统存储能量值S作为描述系统状态的状态量。将C个调度周期作为一个状态，一共有N/C个状态。将一天负荷功率求得平均值，把负荷功率最与平均值的差值取M个区间，负荷功率区间长度ΔPd如下

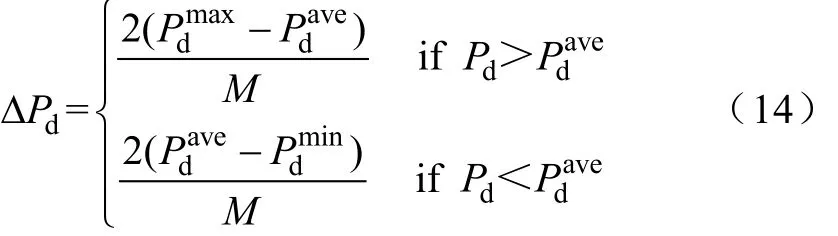
将一天分为两个峰时段和两个谷时段，针对当前调度周期所在时段余下调度周期所需充电或放电的负荷功率，称为剩余所需负荷功率，将其分为 X个状态空间，剩余所需负荷功率这个状态量在所需负荷较小时，可以使得储能系统做出较大充放电动作值决策，而当剩余所需负荷功率较多时，该状态量作用很小；再将当前调度周期所在峰谷区段的最值与一天的平均值之差的绝对值分为Y个状态；储能系统存储的能量分为Z个状态区间。这样系统总共有 N×M×X×Y×Z/C个状态。

3.3 动作策略的选取

1）动作策略集合

Q学习算法只能采用离散的动作值，因此本文将储能系统充放电功率值动作值离散为如下（2h+1）个固定值

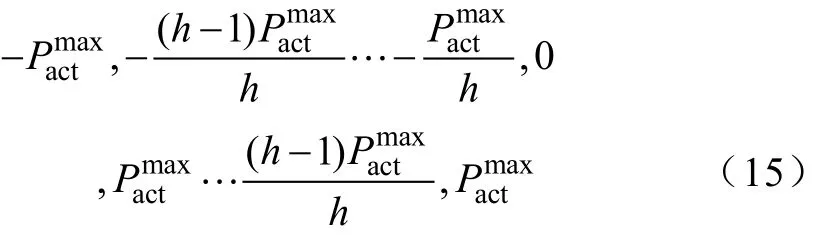
2）动作选择概率

在迭代时各动作的选择采用贪婪策略，贪婪策

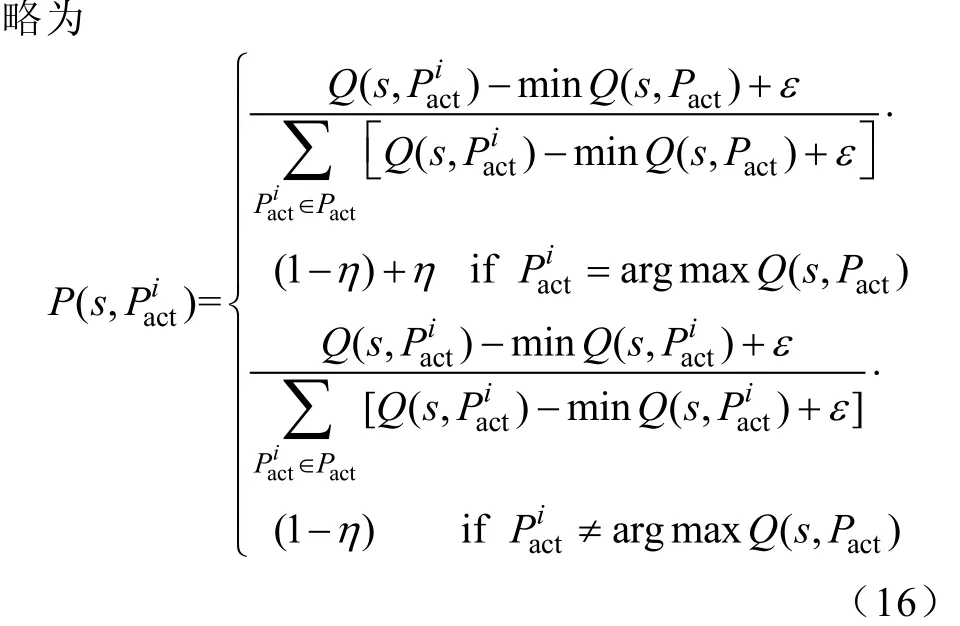
3）动作越限惩罚

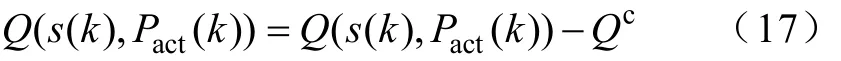
式中，Qc为惩罚值，其值取较大，这样就可以使s(k)状态不再选择动作Pact(k)。

3.4 即时报酬

在Q学习算法中，即时报酬应该为正数，且总的报酬值越大越好，因此将式（1）右边拆开后可以得到

将式（4）求和符号里面的项作为储能系统在每一调度周期充放电动作的即时报酬，为使每一天的报酬值有关联性，每一项都除以每天负荷功率最大值与最小值差的平方，可以得到即时报酬函数如下

3.5 状态量实时修正

Q学习算法是根据状态来做出动作策略的，而负荷功率实际值与预测值存在误差，得到的状态与实际所处状态有偏差，在实时调度周期对描述状态的量进行实时修正，可以使动作策略更准确。由于实时调度周期和储能系统存储能量值这两个状态量与负荷功率预测不准确没有关系，峰谷时段剩余所需负荷功率只与后面调度周期负荷预测值有关，所以只需要实时修正负荷功率平均值和峰谷时段负荷功率的最值。实时调度周期的负荷功率平均值修正方法如下

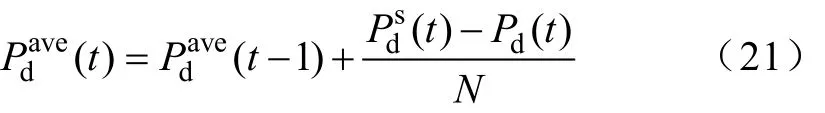
由于考虑到最值和当前峰谷时段取值关系更大，所以将最值预测值直接加上当前时段误差平均值，得到最小值修正方法如下

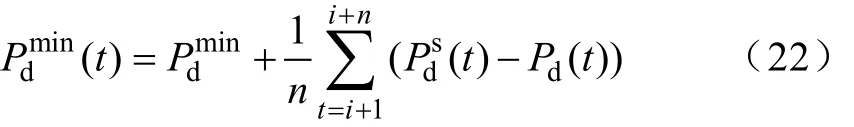
式中，Pmin为当前峰谷时段负荷功率预测值最小值；

d n为该谷时段已经出现的实时调度周期数；i为该谷时段初始调度周期。最大值修正方法与最小值相类似，不再赘述。

3.6 模型求解

基于上文内容，得到整个模型的求解流程如下：

1）初始化各参数值，在学习之前 Q值表中的值取零。

2）初始学习阶段，保持Rc(k)=0，取η=0，即各动作被选择的概率相同，经式（3）用负荷功率离线数据训练，获得储能系统在各状态解耦情况采取不同充放电动作的即时报酬，得到初始Q值表Q1，该阶段并没有进行优化迭代，只是为了得到各状态情况下所有动作策略的即时报酬。

3）获得初始 Q值表后，引入全局优化惩罚项Rc，取η=1，即采用完全贪婪策略，经式（3）和k初始Q值表进行策略的优化迭代，使用离线数据学习得到Q值表Q2。

4）在实时调度周期，储能系统实时修正状态量并判定其所处状态，取η=1，基于训练好的Q值表Q2，采用完全贪婪策略获得其最优充放电动作策略。

4 算例分析

负荷功率数据采用福建省某地区6个月小时级数据，其预测值由小时级气象数据经神经网络拟合得到。因为要应用到实时调度周期，取N=288，C=3，将负荷功率实际值用 spline函数拟合，预测值用线性插值法拟合分别得到 5min的负荷功率实际值和预测值，选取一天出来作为验证负荷。

本文设定有3种模型，这3种模型的目标函数、约束条件、状态空间、动作集合和即时报酬函数都一样，不同点如下。

1）模型Ⅰ

采用传统Q学习算法，取α=0.5，γ=0.8，η= 0 .5，负荷功率为已知值，即实际值与预测值一样，使用式（1）迭代寻优，迭代200次，获得储能系统一天内各调度周期充放电功率最优决策值，所有运算都是离线运算。

2）模型Ⅱ

采用本文所提方法寻优，取 α = 0 .5，完成初始学习阶段得到初始Q值表Q1，负荷功率为已知值，即实际值与预测值一样，使用式（3）优化迭代，迭代200次，获得储能系统一天内各调度周期充放电决策值，所有运算为离线运算。

3）模型Ⅲ

采用本文所提方法寻优，取α=0.5，完成初始学习阶段得到初始Q值表Q1，并使用式（3）用离线数据训练学习得到Q值表Q2，在实时调度周期实时修正其状态量，并基于Q2用完全贪婪策略在线得出最优充放电决策。得到3种模型的净负荷功率曲线，如图1所示。

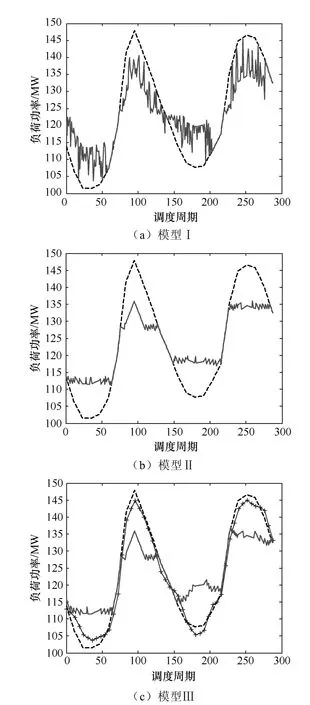
图1 净负荷曲线

图1 （a）中实线为模型Ⅰ得到的净负荷功率值，虚线为负荷功率实际值；图1（b）中实线为模型Ⅱ得到的净负荷功率值，虚线为负荷功率实际值；图1（c）中不带加号实线为模型Ⅲ得到的净负荷功率值，虚线为负荷功率实际值，带加号实线为负荷功率预测值。

3种模型净负荷功率曲线方差见表1。

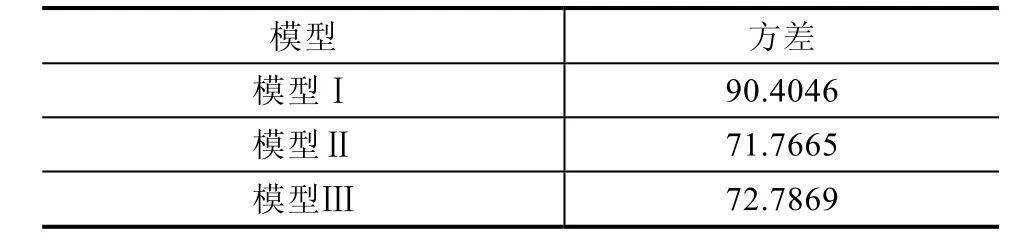
表1 三种模型净负荷功率曲线方差

由表1可以看出，模型Ⅱ削峰填谷效果最好，模型Ⅲ次之，模型Ⅰ最差。模型Ⅰ采用传统Q学习算法迭代得到储能系统最好充放电策略，由图1（a）可以看出，虽然具有一定削峰填谷效果，但是充放电动作值连续性较差，变化幅度较大，与理想最优策略相差较大，还需要进一步的迭代以及参数的调整。模型Ⅱ采用本文所提的寻优方法，得到的削峰填谷效果很好，并且相同条件下迭代完成后得到的动作策略是一样的，而模型Ⅰ每次迭代完成后得到的结果是不一样的。模型Ⅲ第一个谷时段和峰时段得到的净负荷功率曲线已接近模型Ⅱ，这是因为当剩余负荷功率相对于储能系统可用充放电功率较大时，其充放电动作的选择与该时段的最值以及当前调度周期的负荷功率相关性较大，而在该峰谷时段内，预测值与实际值误差都为正或者都为负，最值的修正较为准确，得到的充放电动作决策也会较为准确。对于第二个谷时段，负荷功率预测值与实际值误差正负号多次变化，最值的修正误差较大，状态判断不够准确，得到的动作策略与模型Ⅱ动作策略差距较大，而在第一个谷时段和第二个峰时段也有负荷功率预测值与实际值误差正负不一致情况，但出现的时间在峰谷时段后半段，对最值的修正影响不大，所以其动作策略与模型Ⅱ动作策略相差不大。

5 结论

本文基于Q值表的记忆功能，提出改进的Q学习算法，去掉了遗忘因子，将不同状态下即时报酬之间的关系解耦，用全局最优惩罚项引导算法收敛，使储能系统获得一天的最优充放电动作决策，这种方法是基于初始Q值表对各种状态情况下采取不同动作的即时报酬有了认识以后才进行的，相比于传统Q学习算法，其收敛速度更快，准确性更高，迭代完成后的结果具有惟一性。而且，Q值表具有记忆功能，在实时调度周期不需要因为负荷功率预测值不准确而重新进行迭代寻优，只需修正并判断其当前所处状态，基于训练好的Q值表使用贪婪策略可快速获得当前状态最优动作值。但是这种方法需要较大的内存存储Q值表中的数值，后续工作可以考虑如何减少状态总数，从而减少Q值表中的值，以避免维数过大。

附录A

目标函数为

所以，此时当a≤c时，只需要b=0和d=b+d，当a＞c时，只需要b=b+d和d=0，那么(a − b )2+(c − d )2可以获得最小值。只有当a≤c时，t0调度周期需要减少充电动作值，此时c − a＞ b + d 可以得到c−d＞a+b≥a−b，即有c − d＞ a − b ，此时t0调度周期充电动作值b应该减小b。

当|a − c | ≤b + d 时，

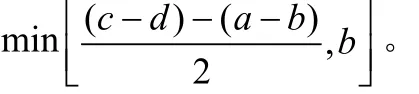
2）同时释放功率

此时 a ＜0 ， b ≤ 0 ， c ＜0 ， d ≤ 0 ，且a、c和(b + d)为定值，且a + c ≤ b + d 。

若|a − c | ≤|b + d|，有

所以，当a≤c时，只需要b=0和d=b+d，当a＞c时，只需要b = b + d 和 d = 0 ，那么 ( a − b )2+ ( c − d )2可以获得最小值。

当 t0调度周期为充电动作而 t调度周期为放电动作时，c − d ＜ a − b ；当t0调度周期为放电动作而t调度周期为充电动作时，c − d＞ a − b ，两种情况都与上述情况正好相反，所以不会影响。

[1] 李乐. 微网的经济运行研究[D]. 北京: 华北电力大学, 2011.

[2] 张明, 朴政国. 含储能的分布式光伏并网系统对配电网调峰的研究[J]. 电气技术, 2016, 17(12): 11-14, 19.

[3] 孙建龙, 窦晓波, 张子仲, 等. 直流对等式微电网混合储能系统协调控制策略[J]. 电工技术学报, 2016,31(4): 194-202.

[4] 李锐, 李鹏. 储能系统在孤岛微网中应用[J]. 电气技术, 2014, 15(6): 15-18.

[5] 李建林, 马会萌, 惠东. 储能技术融合分布式可再生能源的现状及发展趋势[J]. 电工技术学报, 2016,31(14): 1-10, 20.

[6] 刘皓明, 陆丹, 杨波, 等. 可平抑高渗透分布式光伏发电功率波动的储能电站调度策略[J]. 高电压技术,2015, 41(10): 3213-3223.

[7] Chaouachi A, Kamel R M, Andoulsi R, et al.Multiobjective intelligent energy management for a microgrid[J]. IEEE Transactions on Industrial Electronics, 2013, 60(4): 1688-1699.

[8] 宋晓英, 王艳松. 基于协同进化遗传算法的微网经济环保调度[J]. 电力系统保护与控制, 2014(5):85-89.

[9] 李秀磊, 耿光飞, 季玉琦, 等. 考虑实际运行的配电网电池储能系统的优化配置研究[J]. 电力系统保护与控制, 2017, 45(9): 88-94.

[10] Lee T Y. Operating schedule of battery energy storage system in a Time-of-Use rate industrial user with wind turbine generators: a multipass iteration particle swarm optimization approach[J]. IEEE Transactions on Energy Conversion[J]. Sept, 2007, 22(3): 774-782.

[11] 李树雷, 展海艳, 薛松, 等. 考虑间歇性分布式电源并网的分布式储能系统最优控制策略[J]. 华东电力,2013, 41(11): 2338-2343.

[12] 鲍冠南, 陆超, 袁志昌, 等. 基于动态规划的电池储能系统削峰填谷实时优化[J]. 电力系统自动化,2012, 36(12): 11-16.

[13] 高雪莹, 唐昊, 苗刚中, 等. 储能系统能量调度与需求响应联合优化控制[J]. 系统仿真学报, 2016, 28(5):1165-1172.