永磁同步电动机电感参数测量的研究综述

章金晶 汤宁平

（福州大学电气工程与自动化学院，福州 350108）

随着永磁同步电动机在各领域的应用不断推广，对其控制性能也提出了更高的要求，例如较高的跟踪精度、快速的响应能力、良好的容错性[1-3]等。伴随着这些要求存在的一些控制策略，例如弱磁控制、无速度传感器设计等也都是基于电动机精准的参数实现的，它是实现整个控制系统设计、系统稳定性分析以及模拟现场环境的半实物仿真的重要基础。尤其对于电感参数而言，在电动机实际运行时，会受各种因素的干扰而发生变化，并且不同的测量方法得到的电感值与初始设计值之间也会存在误差，因此对于电感参数的辨识研究具有很重要的现实意义。

为了能够准确快速地辨识出 PMSM 的电感参数，国内外学者已开展了大量的研究工作，并取得了不少的优良成果。现如今的电感测量方法一般有直接负载法、矢量控制法、最小二乘法、卡尔曼滤波法[4-5]等。由于电感参数在电动机实际运行时容易受到其他因素的干扰，且各类辨识方法也存在一定的局限与不足，因而本文在此针对现有的、比较常见的、具有实际应用价值的辨识方法，进行归纳、整理和对比分析，总结出各自的优缺点和适用范围。

1 几种常见的PMSM电感辨识方法

1.1 LCR测量仪（阻抗分析仪）测dq电感

仪器测量法[6]为实验室最基本和最易操作的一种离线方法。LCR测量仪是以微处理器控制的数字式测量仪器，用来测量各种无源阻抗参量，其优点为测试响应速度快、读数便捷、频率范围宽、稳定性和准确度也较高。文献[6]提出了一种利用阻抗测量工具来进行dq电感测量的方法。其基本思想是，通过对永磁同步电动机的被测端阻抗进行两相或三相解耦分析，推导出其等效阻抗模型，当该等效阻抗模取最值（最小与最大）时，可计算测量出永磁同步电动机的dq电感。图1为三相参与解耦的实验接线图。

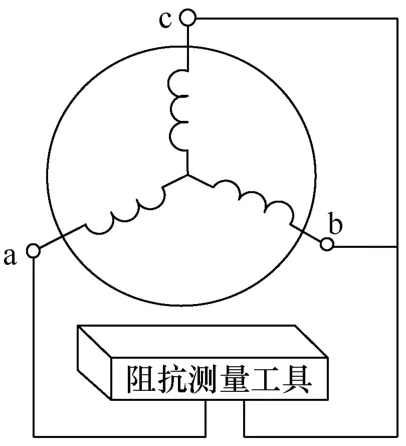
图1 实验接线图

式（1）为等效阻抗的最终表达式，在此省略其中具体的求解过程：

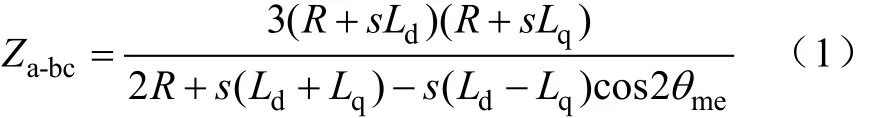
对于永磁同步电动机而言，其交轴电感一般大于或等于直轴电感，该阻抗的模分别在转子位置角为0°和180°时取得最小值和最大值，代入可得永磁同步电动机被测等效阻抗，即

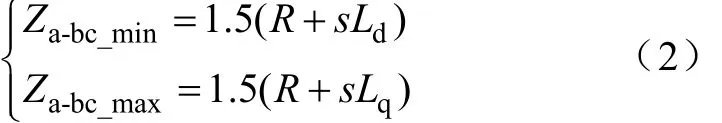
根据上述原理可知，手动搜索转子位置，当角度分别位于0°和180°时，等效阻抗模取得最值，接入阻抗测量仪读出此时的阻抗值，最终可求解出所需的dq电感值。

用此种方法去测量dq电感参数，优点是操作容易、实验装置简单，且LCR测量仪可以保证高精度的测量。但该方法只适合于测量电动机停转时的数据，且受测试电流幅值的限制。并且该种方法无法充分考虑磁路饱和的影响，因而在实际应用的某些场合中，不适合推广使用。

1.2 直接负载法

直接负载法[7-9]也属于实验法常用的一种，原理比较简单，根据电动机发电或电动运行时的相量图，得出交、直轴电感的计算公式，再对公式中的各个参数进行测量，例如电压、电流、功角等，即可得到所需的电感参数，能比较真实地反映电动机的实际运行状况。图2为永磁同步电动机发电状态下的相量图，此时带感性负载。

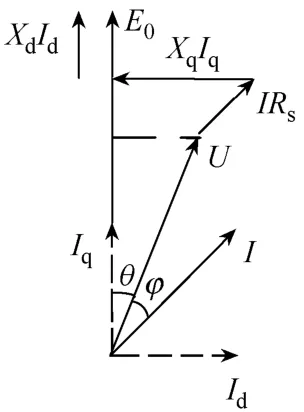
图2 永磁同步电动机发电状态相量图

由相量图可以得到交直轴电抗的表达式，即

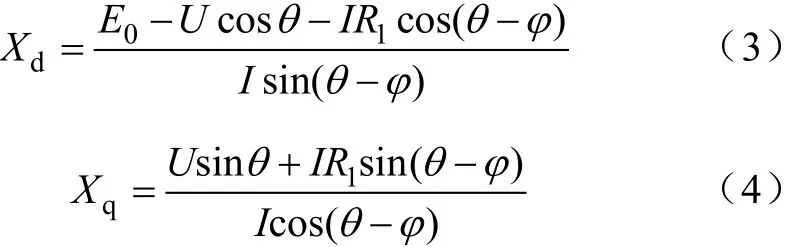
式中，E0、U为永磁体励磁电动势（反电动势），电枢端电压；Id、Iq为定子电流在直交轴的分量；I、R1为定子电流和定子绕组电阻；θ为功率角，即电压和空载电动势的相位差；ϕ为外功率因数角，即端电压与定子侧电流的相位差；ψ为内功率因数角，即定子电流与永磁励磁反电势的相位差。

直接负载法主要通过测量相量图中的各个参量，即可达到最终电感辨识的目的。在实际测量时，电枢端电压、电流和空载相反电势均是通过特定的电参数测量仪器测得，保证了这3个量的测量精度，角度则通过在电动机侧安装编码器测出。

负载法可以充分考虑磁路饱和的影响，且计算量较小，操作不复杂，但是电动机长时间运行或是超额定电流运行时，容易引起电动机发热，进而影响定子电阻阻值发生改变，当电流过大时，定子电阻上的压降影响会较大，从而影响电感值。再者，由于公式里面空载反电动势0E所占的比重较大，其较小的波动也会引起较大的误差，因而对于测量仪器有一定的精度要求，以便提高电感测量的精度。

1.3 基于遗忘因子递推最小二乘法的参数辨识

不同于上述常见的且计算量小的实验方法，不少研究者开始将各种算法以及其他学科领域的知识用于参数辨识，最小二乘法[10-11]为其中较常见的一种。

永磁同步电动机在d-q轴下的电流方程为

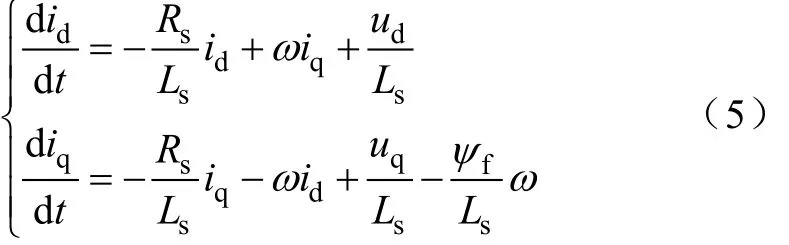
为了实现对永磁同步电动机的参数辨识，在此引用q轴电流方程，对其进行离散化，并且此时采取d0i= 的控制策略，可以得到

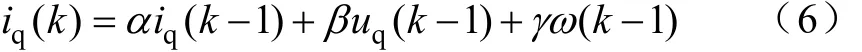
把式（6）转化成矩阵形式可得

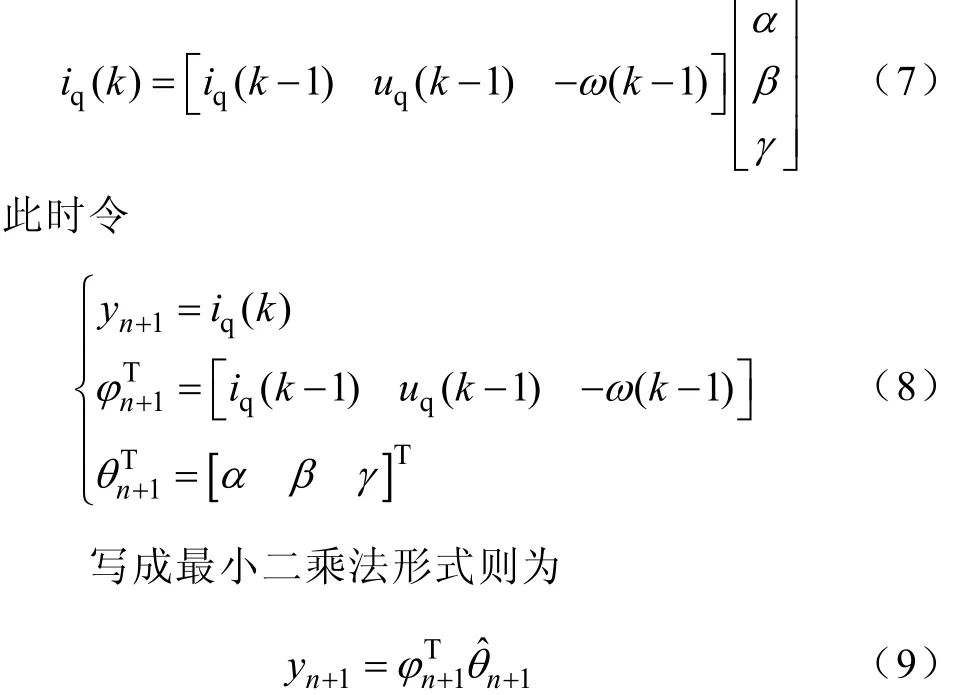
当已知输入量电角速度ω、dq电流、q轴电压时，即可辨识出所需的参数sR、sL和fψ。

遗忘因子的大小直接影响算法的性能，其值越大，算法的鲁棒性会越好，但跟踪能力会下降；反之，跟踪能力增强，但鲁棒性减弱，对外界的干扰和噪声变得敏感。因而该种方法的辨识精度会受遗忘因子的取值大小影响，遗忘因子的大小一般在0～1之间，过大或过小都会对辨识过程造成影响，其稳定性难以保证。

1.4 基于模型参考自适应的永磁同步电动机参数辨识

采用矢量控制的基本策略，得到永磁同步电动机在dq轴下的状态方程如下，此时左端得到的id、iq作为可调模型的输出。

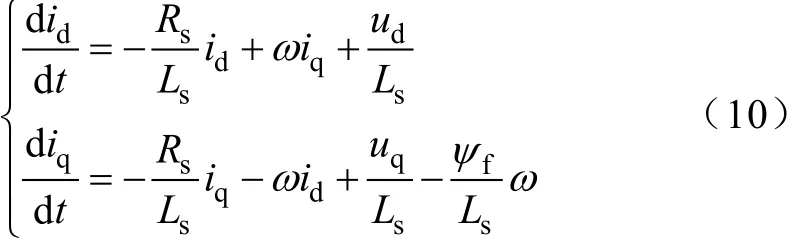
将式（10）表示为

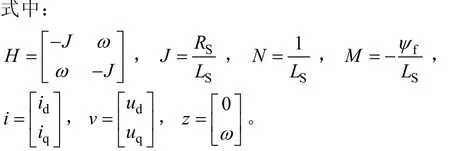
为了引出模型参考自适应算法，在此将式（11）用估计值的形式表示，也即式（12）的可调模型结构：

其基于模型参考自适应的辨识框图如图3所示。

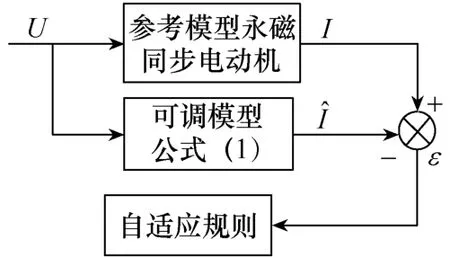
图3 基于模型参考自适应的电动机参数辨识框图

通过波波夫超稳定理论[12]可以得到如下自适应率求解式子：

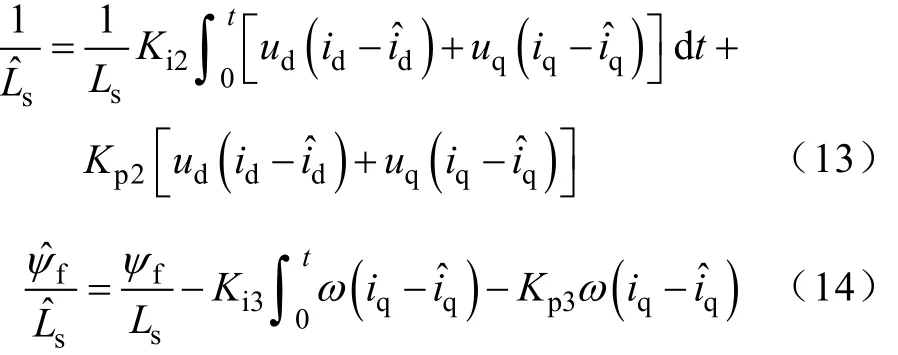
式中，i2K 、i3K 为 PI的积分系数；Kp2、Kp3为 PI的比例系数。该种辨识方法的输入量为dq轴电流和电压的测量值和估计值，即可辨识出定子电阻、定子电感和永磁体磁链。

基于模型参考自适应的PMSM参数辨识方法具有较好的实时性和一定的跟踪性能[13]，但是其整个辨识过程需要的已知输入量较多，容易造成多方面的干扰，输入量的不稳定性易造成辨识精度的下降，故有待进一步优化。

1.5 高频注入法电感辨识

高频注入法[14]是通过在电动机定子端加一个三相平衡的高频电压，该电压幅值限定不大，通过对高频响应信号的分析得到电动机电感参数信息。其原理如图4所示。

图4 高频注入法电感辨识原理框图

从图4中看出，高频电流响应分量、电流基波响应分量、电动机本体谐波分量及逆变器谐波分量等[15]都是电动机高频响应电流信号的组成。因而需要设计合适高效的滤波器来进行滤波，这正是此种方法的一大难点，会使电感辨识过程变得极为复杂。此外，电动机驱动控制系统会用到逆变器，而一般地，逆变器具有非线性效应，会引起逆变输出的电压波形中存在其他阶次谐波，从而降低逆变器的电压利用率[16]，对逆变器的死区补偿性能要求也变高。

2 其他辨识方法的研究

有别于最小二乘法，扩展卡尔曼滤波算法[17-18]是一种适应于非线性时变系统的最优递推估计算法，其通过建立永磁同步电动机的数学模型并加以应用，来达到对电枢电感等各项参数辨识的目的。该方法在电动机实际控制应用时处理的数据量较大，在辨识过程中，系统自身的噪声干扰容易引起辨识结果的准确性和收敛速度。

文献[19-21]提出了比较传统的电感参数测量方法，小直流衰减法和电压积分法。小直流衰减法的基本原理是使电动机电枢绕组中决定磁路饱和程度的大直流电流保持不变，在这个电流的交轴或直轴分量中叠加一个幅值较小的直流衰减电流，通过对后者的辨识来进一步转换得到交直轴电感参数。电压积分法则通过测量电阻和被测绕组构成的电桥中磁链的变化来确定dq电感参数，将电感的测量转化为对电压的积分。两种方法都能充分考虑磁路交叉饱和的情况，但是不易判断出转子的直轴或交轴是否与电动机电枢合成磁势中心轴线重合。且电压积分法中对电阻的需求量较大，而电阻为易发热元器件，此时产生的电阻温漂容易导致电桥不平衡，影响实际的电感测量。

基于模糊神经网络（FNN）的 PMSM 参数辨识[22-23]方法将模糊控制和神经网络两者相结合，来实现永磁同步电动机的非线性参数辨识，具有一定的容错性和鲁棒性。但是FNN一般情况下都没有考虑自身的稳定性问题，且计算量巨大，对硬件的要求也极高。

近年来，也有一些学者将永磁同步电动机参数辨识过程转化为非线性系统的动态寻优问题，章兢团队提出了基于免疫协同微粒群进化算法[24-26]的永磁同步电动机多参数辨识方法，其个体极值采用自适应小波学习算法以加快收敛速度，在实现对sR、fψ、Ld、Lq高精度辨识的同时提高了算法的收敛速度，但由于众多算法的嵌套使用，使得该方法过于复杂，计算量较大。

3 关于电感参数辨识研究的展望

基于遗忘因子的最小二乘法的电感辨识核心在遗忘因子的选取，该值与辨识系统的鲁邦性成正比，与辨识精度成反比，无法两者兼顾。为了增加系统的稳定性，提高辨识精度，研究学者在分析了最小二乘法后相继提出了模型参考自适应法、扩展卡尔曼滤波法、免疫协同微粒群进化算法及模糊神经网络法等来进行电感辨识，有效地解决了前者存在的问题，但是使整个辨识系统变得复杂化，容易衍生出噪声干扰、数据饱和等新问题，且涉及的算法、策略、理论领域较广，对研究者本身的知识储备能力要求较高。LCR仪器法作为实验室最常见的一种电感测量方法，设备的单一性使得无法充分考虑到磁路饱和、运行状态等因素对电感造成的影响。继而学者提出了小直流衰减法、电压积分法、直接负载法和高频注入法，这几种方法对硬件设备具有一定的要求，尤其是高频注入法对逆变器的性能有一定的要求，而硬件设备本身往往会伴随着一些局限性，给实际测量带来困难。

综上所述，大体可以将现今的电感测量方法分为两大类，即在线测量和离线测量。在线参数辨识涉及的知识领域较广，从不同的策略和算法上对参数进行辨识，具有一定的创新性，也能保证一定的辨识精度和跟踪性能，但在辨识过程中容易造成数据饱和，算法也较为复杂。离线测量主要集中在实验测量上，原理会相对较为简单，较少会出现数据冗余，但是易受限于相关硬件的精度及性能干扰，通常需要软硬件结合进行试验，实施过程会相对复杂。关于电感参数辨识的研究，还需我们更深入去寻求出最优的电感辨识方法。

4 结论

本文针对当今存在的常见的电感参数辨识方法进行归纳总结，分析了各自方法中存在的优势与不足。随着现代电动机技术的不断发展，对于永磁同步电动机的各项参数的获取也要求更为精准，尤其是电感参数，它是电动机运行性能的关键指标。因此，对于交直轴电感参数的辨识，将是广大学者的持续研究热点。

[1] Pillay P, Krishnan R M. Simulation, and analysis of permanent-magnet motor drives, part I: the permanentmagnet synchronous motor drive[J]. IEEE Transactions on Industry Applications, 1989, 25(2): 265-273.

[2] Rahman M A, Vilathgamuwa D M, Uddin M N, et al.Nonlinear control of interior permanent-magnet synchronous motor[J]. IEEE Transactions on Industry Applications, 2003, 39(2): 408-416.

[3] 王聪, 关新, 谭骏, 等. 永磁同步电机弱磁性能参数的有限元分析[J]. 电气技术, 2015, 16(7): 16-19, 26.

[4] 王宏, 于泳, 徐殿国. 永磁同步电机位置伺服系统[J]. 中国电机工程学报, 2004, 24(7): 151-155.

[5] 郭仲奇, 罗德荣, 曾智波, 等. 一种新的内置式永磁同步电机弱磁控制方法[J]. 电力电子技术, 2011,45(3): 44-47.

[6] 刘金海, 陈为, 胡金高. 永磁同步电机 dq电感参数新实验获取法[J]. 电工技术学报, 2014(7): 97-103.

[7] 叶芃. 新型同步磁阻电机电感参数的测量[J]. 电气技术, 2016, 17(6): 74-77, 100.

[8] 刘军, 吴春华, 黄建明, 等. 一种永磁同步电机参数测量方法[J]. 电力电子技术, 2010(1): 46-48.

[9] 张健, 刘明基, 陈伟华. 自起动永磁电机电抗参数的测试[J]. 电机与控制应用, 2010(8): 14-18.

[10] 陈涵, 刘会金, 李大路, 等. 可变遗忘因子递推最小二乘法对时变参数测量[J]. 高电压技术, 2008(7):1474-1477.

[11] 赵海森, 杜中兰, 刘晓芳, 等. 基于递推最小二乘法与模型参考自适应法的鼠笼式异步电机转子电阻在线辨识方法[J]. 中国电机工程学报, 2014(30): 5386-5394.

[12] 李旭春, 张鹏, 严乐阳, 等. 具有参数辨识的永磁同步电机无位置传感器控制[J]. 电工技术学报,2016(14): 139-147, 164.

[13] Sun Tao, Kim B W, Lee J H, et al. Determination of parameters of motor simulation module employed in ADVISOR[J]. IEEE Transactions on Magnetics, 2008,44(6): 1578-1581.

[14] 武四辈, 吴志红, 朱元. 车用内置式永磁同步电机电感参数辨识方法[J]. 农业机械学报, 2013(8): 27-32.[15] 张忠英. 基于高频信号注入和卡尔曼滤波器的交流永磁同步电机参数辨识[D]. 南京: 南京师范大学,2012.

[16] 周虎. 永磁同步电机参数在线辨识算法研究[D]. 成都: 电子科技大学, 2012.

[17] 韩晓燕, 刘秀敏. 基于两段卡尔曼滤波的永磁同步电机磁链在线辨识[J]. 微特电机, 2017(5): 36-39.

[18] 肖曦, 张猛, 李永东. 永磁同步电机永磁体状况在线监测[J]. 中国电机工程学报, 2007, 27(24): 43-47.[19] 谢卫. 由直流衰减试验测取同步电机参数[J]. 电机技术, 1992(1): 33-34.

[20] 李颖, 谢卫, 周新. 用电压积分法测定同步电机交叉饱和电感[J]. 电机技术, 2003(2): 6-7.

[21] 唐任远. 现代永磁电机与理论[M]. 北京: 机械工业出版社, 1997.

[22] 曹先庆, 朱建光, 唐任远. 基于模糊神经网络的永磁同步电动机矢量控制系统[J]. 中国电机工程学报,2006(1): 137-141.

[23] 田明秀. 永磁同步电动机的模糊神经网络控制方法研究[D]. 沈阳: 沈阳工业大学, 2006.

[24] 刘朝华, 章兢, 李小华, 等. 免疫协同微粒群进化算法的永磁同步电机多参数辨识模型方法[J]. 自动化学报, 2012, 38(10): 1698-1708.

[25] A new optimizer using particle swarm theory. Eberhart R C, Kennedy J. Proceedings of the Sixth International Symposium on Micromachine and Human Science.1995.

[26] Leesy, Kwarksy, Jungsy. Analys is of inductance characteristic in interior permanentmagnet synchronous motor considering in ductance variation[C]//The 12thbiennial IEEE Conferenceon Electromagnetic Field Computation, 2006: 145-148.