同步磁阻电动机无位置传感器控制的自起动方法

2018-03-01林卫鹏汤宁平章金晶

电气技术 2018年2期

林卫鹏汤宁平章金晶

（福州大学电气工程与自动化学院，福州 350108）

同步磁阻电动机相比于其他电动机具有成本低、无铜耗、效率高、转矩脉动小且不存在高温失磁及弱磁扩速难等一系列优点，是一种十分高效的电动机。

对于高性能的电动机调速系统而言，通常需要在转子同轴上安装机械式传感器以用于检测转子位置角及转速信息，从而实现转速、电流双闭环控制，但是这也给控制系统带来了一系列的弊端[1]。诸如其增加了硬件系统的成本和复杂性；检测信号也易受外界环境干扰从而降低了系统的可靠性；同时在恶劣环境下，硬件容易受损，进一步增加了系统的维护成本和不稳定性。

为此，近年来，无位置传感器控制的研究成为了一个热点。许多学者提出了诸如基于电动机凸极效应、反电动势、状态观测器、滑模观测器以及卡尔曼滤波器等一些估算方法[2]。但是由于电动机在起动及低速运行下，信噪比较低，从而使得上述方法并不能很好地适用于电动机自起动及低速运行中。因此，文献[3-5]提出了升压升频起动方法，但该方法使电动机运行于速度、电流均开环的状态下，故电流是不可控的，容易产生过流问题。文献[6-7]提出了高频信号注入法，这种方法需要向系统中持续注入一个高频电流，从而容易引起谐波和转矩脉动，同时实现过程较为复杂困难，故动态性能并不理想。

针对上述问题，本文采用了I-f流频法自起动控制策略，该方法在电动机起动及低速运行阶段采用单电流环的闭环控制，而在中高速时平稳地切换到基于滑模观测器的无位置传感器控制，从而实现同步磁阻电动机在全速范围内的无位置传感器控制。

1 同步磁阻电动机的数学模型

图1所示为同步磁阻电动机在αβ 静止坐标系及dq同步旋转坐标系中的向量图。其中us、is分别为定子电压矢量及定子电流矢量；ψs为定子磁链矢量；θr、θi分别为转子位置角、电流角；ωr为同步旋转电角速度；下标d、q表示dq轴分量。

图1 同步磁阻电动机向量图

由图1可得dq同步旋转坐标下，同步磁阻电动机电压方程为

式中，Rs为电动机定子电阻参数；p表求导。磁链方程为

式中，Ld、Lq分别为电动机dq轴电感参数。电磁转矩方程为

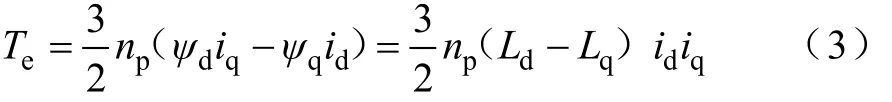
式中，Te为电磁转矩，np为转子极对数。

同时又有

电动机的机械运动方程为

式中，TL为负载转矩，J为转动惯量，αω为给定加速度。

2 I-f流频法起动控制

由式（6）可知，电动机调速过程中需要对电磁转矩进行控制。当在一定负载下、对同步磁阻电动机进行加减速控制、以使其运行在不同的转速下时，需要有相应的电磁转矩。从式（5）可以看出，电磁转矩与定子电流幅值和电流角有关。因此，只需通过控制定子电流矢量，便可进行电动机的调速控制，从而实现单电流环的闭环控制。其控制系统框图如图2所示。

图 3中假定坐标系 dq*模块为与定子电流矢量旋转速度相同且滞后一定角度的dq*旋转坐标系，通过该给定坐标系可将给定定子电流矢量分解成dq*分量，从而实现电动机的解耦控制。角度生成器主要是对给定频率进行积分以获得坐标变换所需的角度θ*，而给定频率又是通过给定加速度积分得到。根据图3所示的给定定子电流矢量与各坐标系间的角度关系，可得坐标变换角为

式中，θf、分别为给定定子电流矢量与α 轴及 d*轴的夹角。

图3 流频法控制电动机向量图

3 起动过程分析

同步磁阻电动机I-f流频法起动主要包含有3个阶段：①转子d轴初始定位阶段；②恒流加速起动阶段；③恒速降流切换阶段[8]。

3.1 转子d轴初始定位

由于电动机在起动运行之前，转子d轴位置是任意的，从而可能造成电动机无法正常起动，为此需要在电动机运行前进行转子d轴初始定位。如图4（a）所示，当向电动机A相绕组中施加一静止的电压矢量时，由于电压矢量与转子d轴间存在一电流角，从而产生一迫使d轴与A相绕组相重合的力矩。如图4（b）所示，当电流角逐渐减小至0时，电磁转矩随之降为0，转子d轴被定位在A相绕组上。

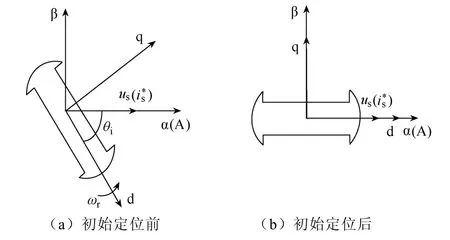
图4 转子初始定位过程

图5 恒流加速起动过程

3.2 恒流加速起动

当转子初始定位完成后，电动机将进入恒流加速阶段。如图5所示，在此阶段，需向电动机中通入一幅值恒定的定子电流矢量，并且使该电流矢量以适当的旋转加速度开始加速旋转至给定速度。由式（5）、式（6）可知，当电流矢量开始由d轴旋转起来后，其与转子d轴间的电流角将逐渐增大，从而产生一随之增大的电磁转矩，直至电磁转矩大于负载转矩时，电动机开始起动加速旋转。在电动机加速至电流矢量频率时，由于加速度的存在，电动机将继续加速运行，从而使得电流角和电磁转矩逐渐减小，直至电磁转矩小于负载转矩，电动机开始减速运行。当电动机电角速度再次与电流矢量频率相等时，电流角和电磁转矩再次逐渐增大。这种反复调整过程，体现了电动机具有“转矩—功角自平衡”的特性。

根据以上分析可得，在定子电流幅值保持恒定下，当负载转矩发生变化时，电动机将通过改变电流角产生与其相匹配的电磁转矩。由式（5）可知，在电流角θi=45°时，电磁转矩达到最大，若此时再加大负载转矩，则会使得电流角大于45°，从而导致电磁转矩下降。在这种情况下，电动机将会发生失步。因此，为了使电动机能够在一定的负载下平稳起动，电磁转矩需要满足以下条件：

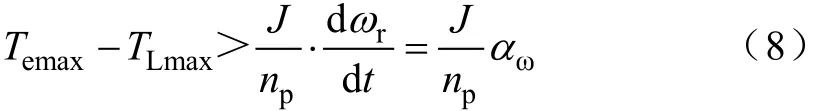
式中，Temax、TLmax分别为起动时刻最大的电磁转矩和负载转矩。

结合式（5）、式（8）可知，当负载一定时，给定加速度αω越大，所需的定子电流is越大。

3.3 恒速降流切换

如图6所示，当电动机达到给定速度时，由于滑模观测器估算的转子位置 dest及转速与实际值间的误差较小，因此可忽略 d轴与 dest轴间的角度误差。与此同时，电动机需由流频法控制切换到基于滑模观测器的无位置传感器控制。

图6 流频法控制的电动机稳态运行矢量图

但是，由于流频法控制是基于dq*假定坐标系下的单电流环闭环控制，而基于滑模观测器的无位置传感器控制则是基于dq转子坐标系下的转速、电流双闭环控制，因此两者间存在一个较大的角度差Δθ，如果直接进行切换，就会引起转矩和转速的震荡。为此，需要先使两个坐标系相互重合，然后再进行两种控制算法间的切换。这样才能保证在切换过程中，电动机能够平稳地运行。

采用SPSS 23.0对数据进行统计学分析。计量资料以表示，Shapiro-Wilk法检验正态分布,Levene法检验方差齐性。当数据符合正态分布,且方差齐性时,多组间比较采用单因素方差分析，两两组间比较采用LSD-t法检验。如数据非正态分布或方差不齐，采用非参数分析Kruskal-Wallis检验方法。对于包含两种处理方式的实验结果，采用析因设计方法进行检验。α=0.05为检验水准(双侧)。

从图6中可知，两算法间能否进行切换的判断依据为两坐标系间的角度差。为了实现电动机的解耦控制且获得在电动机稳态运行下，两个坐标系间的角度差，需要对假定的dq*坐标系进行初始定位。由于同步磁阻电动机的转矩—功角自平衡稳定限制区域为[9]

因此，在转子初始定位时，可假定与定子电流矢量旋转频率相同且滞后转子 d轴 45°的 dq*旋转坐标系，如图7所示。则两坐标系间的角度差为

图7 假定坐标系dq*的初始定位

根据以上对“转矩—功角自平衡”原理的分析可知，当定子电流减小时，电磁转矩随之减小，在达到新的转矩平衡前，功角θi随着转速的减小逐渐增大，从而使得两坐标系间的角度差Δθ 不断减小。当Δθ 减小至某一较小阀值ε 时，、，此时便可进行平顺地切换。其切换过程如图8所示。

图8 恒速降流切换过程

假设定子电流线性减小，则有

式中，t0为降流初始时刻，Ci为降流初始时刻的定子电流平方值，ki为定子电流下降斜率。

且有

式中，ΔθL(t)=2Δθ(t)，kt=3np(Ld−Lq)/4 为常量。

同时，为了简化运算，可假设角度差ΔθL以斜率kθ线性减小，即

从式（17）中，可以看出角度差ΔθL的下降速率kθ正比于定子电流幅值is的下降速率ki，因此通过改变ki值，即可控制切换过程的速度。两算法间能否进行平滑切换的另一个关键条件，就是在角度差Δθ=ε 的同时，电流刚好降到期望值。但是由于机械系统相比于电气系统存在一定的响应滞后，因此过大的ki会导致在角度差Δθ 下降为ε 时，实际电流值已经远小于所需的期望值，甚至出现负值，这将引起切换过程中转矩和速度的脉动。

为了实现切换过程的快速性及平稳性，本文采用了变ki斜率的方法[10]，即在角度差下降到不同阶段时，取不同的电流下降斜率。随着角度差越接近0，ki取值越小，即

式中，k1、k2、k3为定子电流在不同阶段的下降斜率且k3＜k2＜k1；c1、c2分别为角度差下降过程的不同阶段。

4 仿真结果与分析

根据以上分析，可在Matlab/Simulink仿真平台上，搭建如图9所示的同步磁阻电动机全速范围内的无位置传感器控制系统仿真模型。该控制系统采用最大转矩电流比控制，当电动机处于起动及低速运行状态时，3个控制开关被切换到 2位置，即为I-f流频法起动，此时系统为电流单闭环矢量控制；而当电动机处于中高速运行状态时，3个控制开关被切换到1位置，即为基于滑模观测器的无位置传感器控制，此时系统为转速、电流双闭环矢量控制。本文采用的基于滑模观测器的无位置传感器控制主要是先通过滑模观测器观测得到有效磁链，再通过锁相环从有效磁链中提取出转子位置角及转速信息，从而实现无位置传感器控制。

图9 全速范围内无位置传感器控制系统框图

表1 同步磁阻电动机参数

图10 给定转速50rad/s下，由I-f切换至基于滑模观测器的无位置传感器控制的响应波形图

所用同步磁阻电动机参数见表1，仿真中I-f恒流起动阶段给定的定子电流is为7.6A；负载转矩TL为 5N·m；起动加速度αω为 20rad/s2；角度差阀值ε 为 0.5°；k1、k2、k3、c1、c2分别为 5A/s、1.25A/s、0.5A/s、0.4、0.1。仿真结果分别给出了在给定转速50rad/s下，由 I-f起动切换至基于滑模观测器的无位置传感器控制及在给定转速1000r/min下，由I-f起动至 50rad/s后切换至基于滑模观测器的无位置传感器控制的响应波形图。由于在仿真环境下，转子d轴与A相绕组一开始就是相互重合的，即电动机是由 0°初始位置开始旋转的，因此仿真结果未给出转子d轴初始定位阶段的波形图。

由图10可以看出，在恒流加速起动阶段，由于定子电流的闭环控制，使得其幅值始终维持在给定值7.6A。在电动机进入稳态运行后，在6s时开始进行恒速降流切换，在此阶段随着相电流的平滑下降，角度差也逐渐减小，而转速一直维持在50rad/s，并未有较大的波动。在大约 12.5s时，角度差减小至给定阀值，控制系统由I-f流频法控制平缓地切换至基于滑模观测器的无位置传感器控制，切换过程中，转速、角度差以及相电流的脉动都较小。

图11为同步磁阻电动机在I-f流频法控制下，平稳起动并加速至50rad/s及在I-f切换至基于滑模观测器的无位置传感器控制后，电动机迅速加速至给定转速 1000r/min的响应波形图。由仿真结果图可以看出，电动机起动过程较为平缓并且稳态运行时转速较为平稳，脉动较小；同时在算法切换后，电动机对转速突变具有较快的响应速度。这表明了在全速范围内，同步磁阻电动机无位置传感器控制具有较好的稳态及动态性能。

以上仿真结果与理论分析相符合，表明了将I-f流频法控制运用于同步磁阻电动机无位置传感器控制的自起动中是有效可行的，其不仅能够实现电动机较为平缓地自起动，同时还能够较为平稳地切换至基于滑模观测器的无位置传感器控制。